正态重采样的改进行人再识别度量学习算法
宋丽丽,李 彬,赵俊雅,刘国峰
1.成都理工大学 工程技术学院,四川 乐山614000
2.武汉轻工大学 机械工程学院,武汉430023
3.武汉理工大学 理学院,武汉430070
1 引言
行人再识别任务的目的是在监控网络中对跨越摄像头场景的行人目标进行再次识别[1-2]。该技术在安防管理、目标跟踪以及公安系统等领域有着广泛应用前景。行人再识别系统能够有效追溯行人的行为轨迹,查询、定位目标人物,极大程度节省了人力和财力成本,避免了漏检、误检等错误,因此吸引了大量科研工作者投入到该领域的研究中。
基于图像的行人再识别技术,主要通过图像的特征模型,得到其特征向量,然后基于特征向量进行目标的分类识别。因此,人们引入了图像分类识别的相关算法,但由于行人再识别应用场景过于复杂,行人图像受到光照条件、步态、拍摄角度以及背景等因素的影响,导致样本图像分类特征不稳定,行人再识别精度不理想。为了提高行人再识别精度,科研人员主要从以下两个方面进行研究:(1)设计一种鲁棒的具有强分辨能力的外观特征模型;(2)建立一种有效的相似性度量算法。
现有的行人再识别方法主要针对特征表达模型和度量模型。对于特征表达模型的研究,主要基于区域或者分块特征模型方法,其中一些优秀的特征模型是通过结合多种类型的特征,组成混合特征表达。比如:对称驱动局部累积特征(SDALF)[3]、自定义图案结构特征(CPS)[4]、生物学启发特征和协方差描述(BiCov)[5]以及局部fisher向量编码混合特征(eLDFV)[6]等。Yang等人[7]利用color name建立图像色彩特征表达模型,该模型对于光照变化及局部几何变换鲁棒性更强。廖胜才等人[8]利用色彩和纹理直方图建立特征表达方法,提出了LOMO模型,以此计算局部色彩纹理特征,得到一个超高维度的特征向量。虽然上述特征模型在图像外观表达能力和分辨能力上取得了显著的提升效果,但由于行人图像特征变化过于复杂,上述模型对于最终识别精度的提升有限。
在度量模型研究领域,人们针对行人再识别任务的特殊性,提出了更加有效的有监督的度量学习模型。Zheng 等人[9]提出了一种相对距离比较算法(RDC),该算法通过约束正样本距离小于负样本来学习距离度量的投影空间。Köstinger M等人[10]则通过统计推断的方法,提出了KISSME 度量模型。Weinberger 等人[11]通过约束样本的k 近邻样本相似性与负样本相似性之间的距离,来学习一个决策边界。Jing等人[12]则通过半耦合低秩字典表达的方法度量模型,提出了SLDDL算法,并进一步改进,建立了多视角的MVSLDDL行人再识别算法[13]。Liao 等人[8]则结合KISSME 算法和FDA 算法,建立了一种交叉二次判别模型(XQDA)。Gao等人[14]利用字典表达的方法,学习一种具有视觉不变性的正交字典,提升了模型的分辨能力。Li等人[15]则引入深度学习等方法,建立了FPNN深度网络模型。Ahmed等人[16]在FPNN 的基础上,利用人体结构信息,提出了Improved Deep深度网络结构。
通过上述算法,行人再识别任务的识别精度得到了显著的发展,但是行人再识别中样本特征变化过于复杂,现有数据库所包含的行人外观特征变化远少于实际,这导致度量模型在训练数据上过拟合。因此,本文通过半监督学习方法对度量学习算法进行改进,以此提高度量模型对测试样本的鲁棒性。本文创新点主要有:
(1)在原有度量模型基础上,提出了一种半监督学习方法,有效地改进了算法泛化能力。
(2)对现有度量学习算法识别精度低的根本原因进行了深入分析,得出过拟合问题导致算法泛化能力弱的结论。针对该问题提出了一种重采样的方法,在增加样本的多样性的同时,增强了度量模型对待识别样本的适应性。
(3)针对半监督方法对度量模型分辨能力的弱化问题(rank >10 的识别精度下降)。本文提出了一种组合度量策略,在增强了模型泛化能力的同时,保障了模型的分辨力。
2 行人再识别与交叉二次判别算法
2.1 特征提取
基于度量学习算法的行人图像相似性度量,需要首先将图像转化成外观特征描述。由于行人跨越监控场景时外观变化的复杂性,因此特征模型的鲁棒性对于最终识别结果至关重要。本文选取LOMO特征模型对行人图像特征进行表达,包含HSV空间下和Lab空间下的色彩直方图以及SILTP纹理直方图。
如图1所示为特征提取模型,首先将原始图像分割成尺寸为8×16 的局部像素块,然后对每个局部像素块提取HSV空间和Lab空间下的色彩直方图,并将每个通道压缩为24个级数,随后通过LBPs算子提取图像的局部纹理特征。但该特征维度过高,不便于进行度量子空间的学习。因此,基于PCA算法学习一个投影子空间,对原始图像外观特征进行降维。
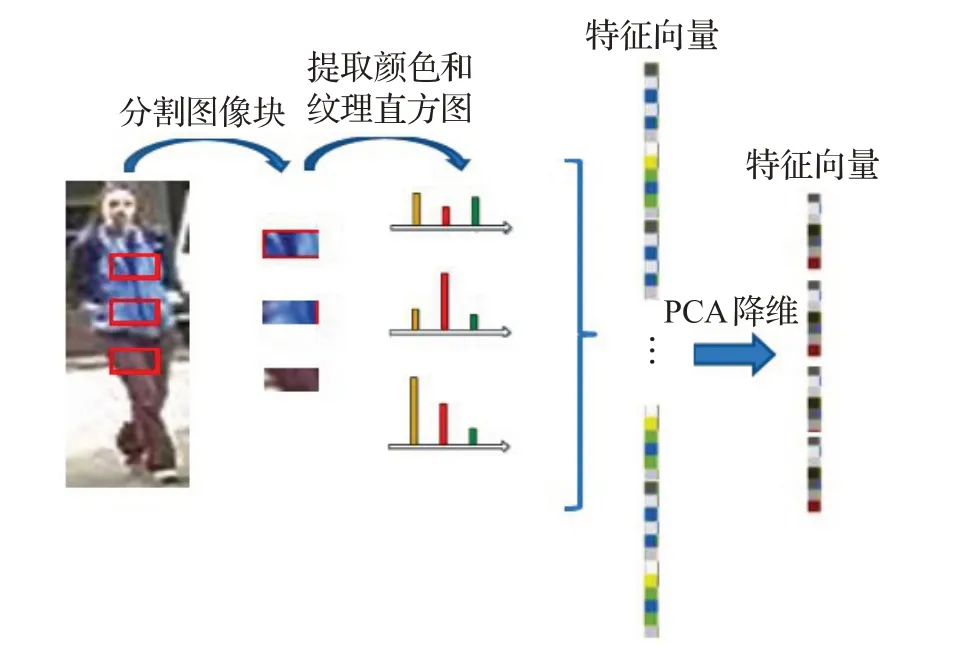
图1 特征模型
2.2 相似性度量模型
行人图像面临着光线、背景以及几何变换等各种问题,导致图像特征十分不稳定。在对样本进行度量时,基于欧式距离等度量方法由于图像中行人空间分布的错位问题,无法有效地对行人图像的相似性进行比较。此外,基于欧式距离的判别分析度量模型在VIPeR数据集上的rank-1识别精度只有35.49%,而基于马氏距离的识别精度则达到了40.02%。因此,本文选取了马氏距离,基于样本的正态分布假设,在投影子空间中,建立统计样本的统计推断模型。
行人再识别研究的难点,在于两个不重叠摄像头得到的行人图像相似性匹配问题。给定样本集和样本集分别表示两个摄像头拍摄到的行人图像特征,xAi为A 摄像头下的第i 个人,xBj为B 摄像头下的第j 个人。用表示一个待识别的样本对,lij则表示该样本对的标签。lij=1 表示正样本对;反之lij=0 表示负样本对。行人再识别任务就是对的样本特征相似性进行度量。目前基于度量学习的行人再识别方法,是对两个样本特征的差向量进行处理。定义表示一个待识别样本对中两个样本的特征差向量,因此行人再识别问题转化为对特征差向量的二分类问题,即判别lij=1 或0。样本相似性通过定义一个相似距离来进行度量,欧式距离等传统距离度量方式的识别结果精度较差。因此,通过学习一个马氏距离,来优化样本的相似性度量,如式(1)所示:

其中,M 为马氏距离的度量矩阵。行人再识别度量学习模型的目标是学习一个距离,使得在该距离度量空间中,正样本对距离小于负样本对的距离,由此得到相对距离函数:
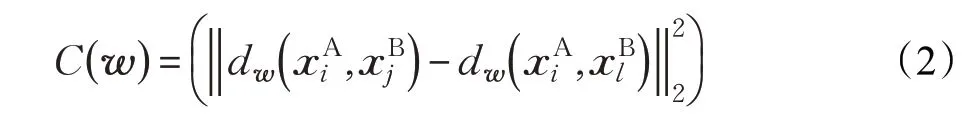
通过最小化所有样本的相对距离总体,建立距离度量模型的目标函数:
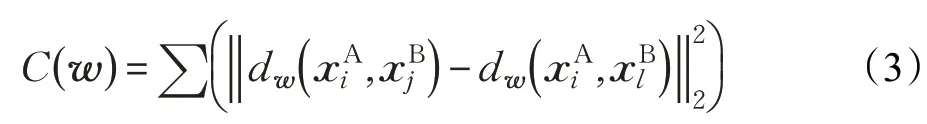
2.3 基于交叉二次判别分析的行人再识别算法
交叉二次判别分析(XQDA)算法[8]是一种基于Fisher判别分析(FDA)算法理论,建立的行人再识别度量学习模型。该算法包含两个方面:(1)学习一个度量投影子空间,使得正样本对总体散度尽量小,负样本对总体散度尽量大;(2)在投影子空间中学习一个马氏距离。
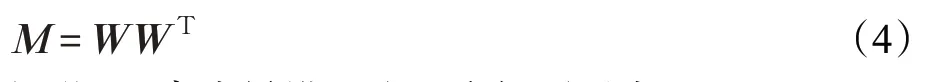
因此,距离度量模型改写为如下形式:
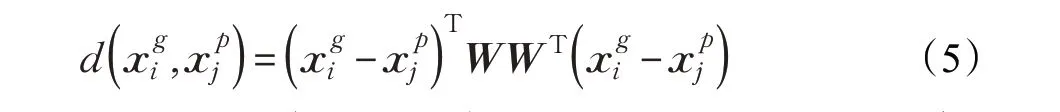
其中W 可以看作为差值特征向量的子空间投影矩阵。于是行人再识别度量学习问题转化为一个投影子空间的学习问题。对于该子空间的学习,投影矩阵W 的目标是使得在投影空间中,正负样本对总体之间的差异尽量大,类内散度尽量小。

其中SI,SE分别表示正负样本对总体散度。
投影子空间的学习通过解决最大化式(8)所示的Fisher判别函数的优化问题来实现。

式(8)所示的Fisher判别准则等价于如下形式:

式(9)所示的问题可以通过拉格朗日方法来求解。于是公式(9)优化问题转化为广义的特征根问题:

此外,基于正负样本对的总体分布假设,在投影空间内学习一个马氏距离来提高样本相似性度量的效果。从统计推断的角度看,待检测样本对(的相似性优化决策方案,可以通过样本对分布概率的统计推断模型进行求解:

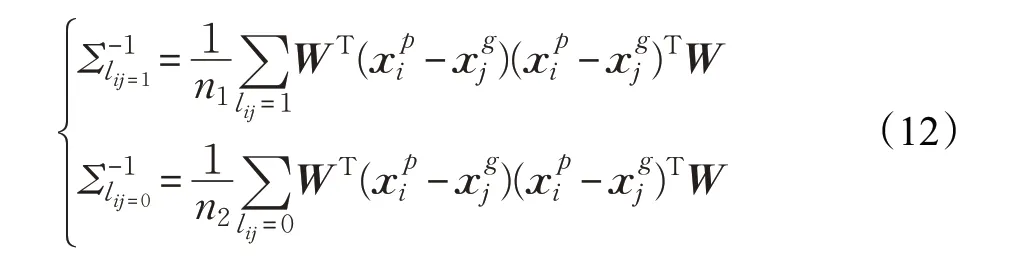
3 改进的交叉二次判别算法
针对行人再识别小样本问题导致的度量模型的偏差问题,本文引入半监督学习理论,设计完成了一种基于样本正态性重采样的迭代优化度量学习模型。
3.1 半监督的交叉二次判别分析度量学习算法
交叉二次判别分析算法的假设前提是训练样本与测试样本服从相同的分布。然而,由于训练数据与测试数据均为样本总体的极小一部分,导致了基于训练样本的模型参数估计是有偏的,使得度量模型对训练样本过拟合,故该假设与实际情况不符。本文利用已有的有限数据,通过提升度量模型的适应能力和分辨性,去提升度量学习算法的识别精度。本文涉及的设计方法分为两个部分,首先通过度量模型对样本进行相似性度量,得到初始度量结果。然后通过度量结果产生潜在相似样本对,再利用半监督学习方法对度量模型进行修正,最后将基于训练样本的度量模型扩展到测试样本,以增强模型的泛化能力。

将待识别样本与k 个最近邻样本任意组合,可以得到k 个潜在相似样本对。同时除去k 个最近邻样本,并在剩余样本中随机选取k 个样本,对应得到k 个负样本对。本文提出的重采样方法是为了增强度量模型对于待识别样本的适应性,增加样本的多样性,提升算法的泛化能力。对于潜在样本选取,本文在初始度量空间中,选取与待识别样本相似性最高的k 个样本组成样本对。这些样本对为潜在的相似样本,在外观特征上存在很大相似性,从而实现对模型适应性的改进。对于k 值的设置,本文通过实验的方法,综合考虑算法的计算复杂度,设置参数k=3。
通过潜在正样本对和负样本对,得到虚拟标签信息,并对于每个待识别的样本,都可以得到k 个正(负)样本对,通过潜在正样本对Pi和任意潜在负样本对Pi′ ,得到k 个具有虚拟标签的数据集,带入交叉二次判别分析模型中进行训练,得到新的度量模型:
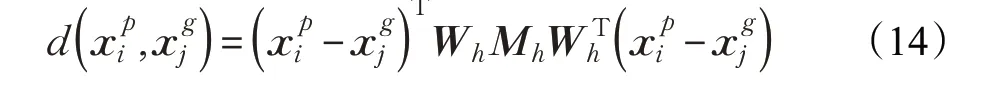
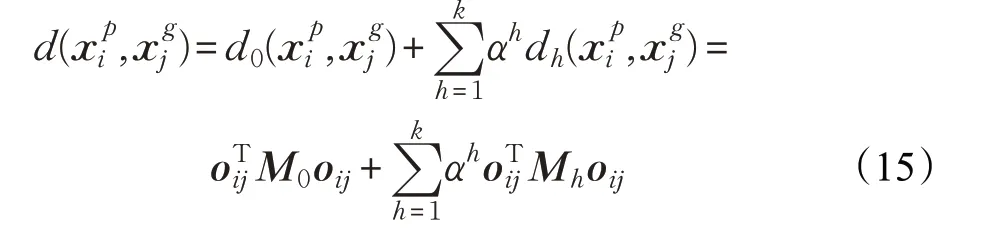
其中,α 表示虚拟度量模型的权重参数,且0 <α <1。
通过上述操作,得到联合度量模型,对测试样本进行相似度量,得到新的度量矩阵D2。通过对度量结果的排序,可以得到新的虚拟标签信息,重复上述的半监督学习过程,并进行循环优化,从而得到新的相似度量模型,结合每次循环优化产生的度量模型,建立循环优化的半监督度量模型,如公式(16)所示:

其中,c 表示循环的次数,β 表示循环优化权重参数,且0 <β <1。
3.2 计算方法
基于本文提出的循环优化半监督度量学习模型,设计行人再识别方法如下所示:输入:带标签的训练集XL和无标签的测试集XT。
(2)通过初始度量模型对无标签的测试样本进行识别,得到相似距离矩阵D1。
(3)对相似距离进行排序,选取前k 个样本组成潜在相似正样本对{ }Pi,随机选取k 个负样本组成负样本对
(4)将潜在的正样本对和负样本对按照排名组成虚拟数据集,根据公式(10)和(12)学习得到新的度量模型。
(5)根据公式(16)计算半监督学习的联合度量结果,并对测试样本进行相似度量,产生新的相似距离矩阵D2。
(6)重复步骤(2)~(5),并通过公式(16)进行相似距离度量,直到循环次数满足终止条件m=c。
根据KISSME 和交叉二次判别分析的行人再识别模型方法,假设行人图像正、负样本对的特征差向量分别服从不同参数的正态分布,且0均值,即O+~Ν(0,Σ+),O-~Ν(0,Σ-)。在交叉二次判别分析模型中,通过学习一个投影子空间W ,使得正样本散度SO+远远小于负样本散度SO-。然而,通过VIPeR数据集上实验统计结果发现,测试数据中正样本对到分布中心的平均距离为142.3,计算方法如下:
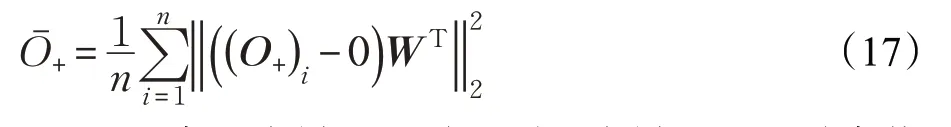
因此,现有的度量模型学习到的度量子空间是有偏的,度量子空间对训练数据过拟合,从而导致模型的泛化能力较差。
典型的行人图像外观特征向量维度数以千计,而训练样本图像数量则远低于维度数。行人图像特征的总体分布是未知的,并且以现有的数据样本是难以估计的。即使得到该样本总体,利用体量如此庞大的数据进行子空间的学习,其计算量过于庞大,也是无法实现的。
本文提出的半监督方法,采用一种新颖的方式,在无法求得行人图像总体分布的情况下,通过邻域重采样方法,对度量模型进行修正,使得待识别样本中的正样本对(),在投影空间中尽可能靠近训练数据的分布,即:

然而,待识别样本对应的正样本对是求解目标,是未知的。本文利用半监督的方法,找到潜在目标,对度量子空间进行修正。对于每个待识别的样本,其邻域内包含了真实的匹配图像或外观特征相似的图像。为了提高目标函数(18)的概率值,本文重新计算投影子空间W ,使得待识别样本加入后的正样本对散度尽可能小于负样本对总体的散度,即:

4 仿真实验
4.1 数据库与仿真设定
本文研究中选取了VIPeR 和CUHK01 两个数据集对本文算法的精度进行验证。VIPeR[3]数据集是最早被公开的用于行人再识别任务的图像数据库之一。该数据库包含了2个不同户外监控场景中拍摄到的632个行人,由于每个行人在每个场景中仅有一张图像,因此数据库共有1 264 张行人图像。且每张图像尺寸为128×48像素大小。CUHK[6]提供了多种场景和假设的测试环境,是目前数据量最大的数据库之一。该数据库中每个行人在统一摄像头下对应多张图像。本文使用的是其中CUHK01 数据库,它共包含有971 个行人的样本图像,其中每个行人在同一摄像头下均有2 张样本图像,库中所有图像样本均被归一化到160×60的尺寸。
为了与其他算法进行对比,本文采用常见的测试策略,即将样本通过随机抽样的方式,平均分为两个部分,分别用以模型的训练和测试。此外,设定算法参数,本文设定c=1,α=0.8,β=0.3。
4.2 评价指标
本文使用累计精度曲线(CMC curve)[5,13]作为算法识别精度的评价指标,计算方法如下:
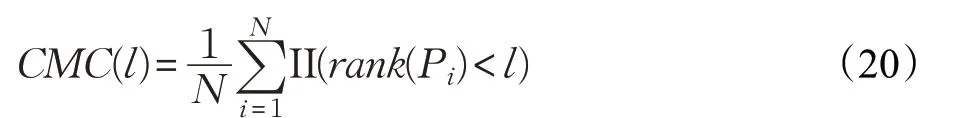
其中,l 表示CMC 累积精度的rank=l ,即测试距离按照从小到大的排名为l,N 为测试样本中gallery的样本个数。II(⋅)为符号函数,即函数内变量为真时则对应函数值为1,否则为0。rank(⋅)表示样本距离排名计算,Pi为第i 个gallery 样本的正样本距离,rank(Pi)表示其正样本的排序。
4.3 仿真实验
基于LOMO 特征模型提取得到的行人图像特征是一个超高维的特征向量,不利于计算。本文通过PCA降维,基于投影得到投影特征并进行度量子空间的学习。PCA投影矩阵与度量学习得到的投影矩阵融合,得到投影子空间中的度量投影矩阵。如表1 所示给出了不同PCA 投影维度下的算法识别精度统计结果(c=1、β=0.3)。

表1 算法识别精度统计表
由表1中的统计结果可以看出,PCA投影特征维度不同,则对应的识别精度也不同,当PCA 维度超过150时,算法的精度变化不明显,设置基本不变。这是因为原始的高维特征中包含了大量冗余变量,通过PCA 降维得到主要的分辨信息的同时,有效保留了信息的完整性。此外,PCA降维还显著减小了算法的计算复杂度。
如表2 所示为基于VIPeR 数据库进行10 次重复独立实验,计算平均值作为识别精度的测试结果。如表2所示,给出了rank-1、rank-5、rank-10和rank-20识别精度的统计结果。从表中数据可以清楚地看出,本文算法在所有指标上均取得了最优的识别结果,尤其在rank-1的识别精度上,相较于MLAPG 算法精度提升了7.79%。此外,本文给出了迭代次数c=2、β=0.3,c=1、β=0.8 以及c=1、β=0.3 三种参数条件下的识别精度。从结果可以看出,迭代次数增加虽然能够一定程度上提升rank-1的识别精度,但使得rank >5 的识别精度存在显著下降。而当β=0.3 时,rank-1 具有稳定的识别精度,且能保证rank >1 的识别精度。训练数据量p=316,即316个行人的数据用于训练。

表2 算法识别精度统计表
此外,本文对不同c、β 和α 取值下的算法识别精度进行了分析,从而选取合适的参数设置。如图2 所示,给出了三个参数在不同值设置下排序前1、前5、前10和前20的识别精度值,根据精度的变化,本文设置c、β 和α 的参数值分别为2、0.3 和0.8。其中,在测试c 的参数灵敏性时,固定β=0.5,α=0.5。测试β 时,固定c=1,α=0.5,测试α 时,固定c=1,β=0.5。
图3 中选取了排名前50 的累积识别精度绘制曲线。从图中可以看出,本文算法的识别精度在所有对比算法中达到了最优的识别精度。
本文对不同训练数据量大小下的算法识别精度进行了测试。如图4 所示,给出了训练数据量在p=316、200 和150 三种条件下的算法识别精度,从图中可以看出,当训练数据量大小显著下降时,本文算法能够保持较高的识别精度,对于训练数据量大小的变化具有较强的鲁棒性。
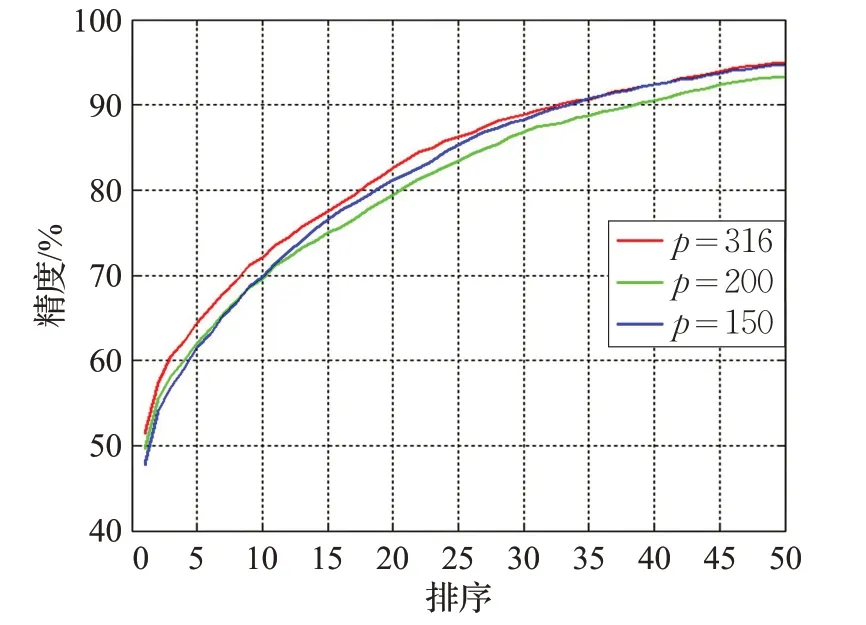
图4 不同训练数据大小下的算法识别精度对比
此外,本文在CUHK01数据库上对本文提出的算法进行了识别精度测试,训练数据量p=485,其识别精度对比结果如表3所示。从表中可以显著看出,本文算法具有良好的识别效果,在所有选定排名上的识别精度均达到了最优识别结果,尤其在rank-1上的识别精度达到了69.66%,超过了最好的对比算法NFST算法4.68%。

表3 行人再识别在CUHK01数据库上的测试结果
本文算法在现有度量学习算法的基础上进行了改进,提出了一种半监督的度量学习模型,算法的核心在于通过特征根问题的求解,计算投影子空间。该部分的计算复杂度与矩阵的维度有关,是一个O(N3)的算法,随着矩阵维度的增加,计算复杂度呈3次方增长。本文循环优化的方法会提高计算复杂度,具体与迭代次数相关,是一个c×O(N3)的算法,c 为迭代次数。但同时本文算法有效提高了算法的泛化能力和鲁棒性,可以大大减小矩阵维度需求,提升计算效率。
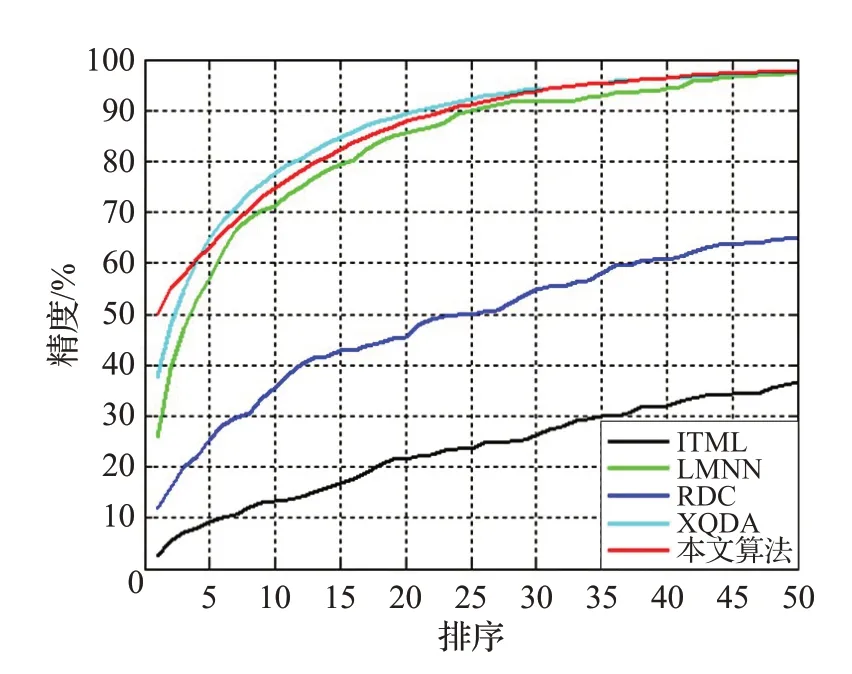
图3 算法识别精度对比
如图5 所示给出了交叉二次判别分析算法和本文改进算法在不同矩阵维度下rank-1 识别精度。图中曲线所示为在不同矩阵维度下的识别精度。可以看出,本文算法在较低维度下即可快速达到较高的识别精度。现有的交叉二次判别分析算法则的特征维度为316。本文设置矩阵为100,大大减小了矩阵维度和计算量。
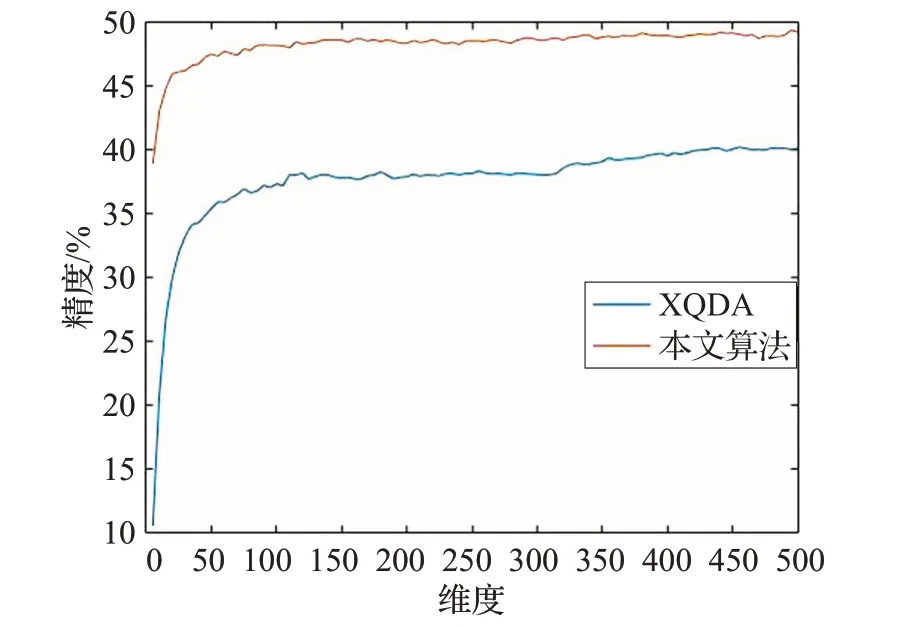
图5 不同矩阵维度下rank-1识别精度
对比一些优秀的算法,本文算法耗时统计结果如表4所示。

表4 算法耗时在VIPeR数据库上的测试结果
5 结束语
本文提出了一种基于样本正态分布假设的重采样度量学习算法。首先,在样本初次识别时,采用交叉二次判别算法,学习得到现有样本初始度量,并计算样本马氏距离;其次,基于样本特征的正态性,对待识别样本进行重采样,产生潜在相似样本对和训练数据。然后,将重采样后的数据集代入度量学习模型循环训练,得到新的度量模型。接着,重采样后训练的泛化模型与初始有监督的度量模型,通过综合加权建立了新的联合度量模型。最后,基于联合度量模型结果,重复半监督学习过程进行循环优化,计算联合相似度量,并输出最终结果。为了验证本文方法的有效性,实验选取了VIPeR和CUHK01两个数据库对算法进行了测试,测试结果显示本文算法在rank1,rank2,rank3,和rank4 等级别的准确率均优于改进前的交叉二次判别算法和相关行人再识别算法,尤其在rank-1 上的识别精度分别超过了MLAPG 算法和NFST 算法7.79%和4.68%,且本文算法对于训练数据量的变化具有较强的鲁棒性。

