基于遗传退火优化的小波神经网络预测模型

朱如鹏，俞莎莎，李苗苗，赵英豪，王宇

(南京航空航天大学 机电学院，江苏 南京 210016)

0 引言

预测是根据客观事物过去和现在的发展规律，借助于科学的方法对其未来的发展趋势和状况进行描述和分析，并形成科学的假设和判断。BP神经网络[1]具有高度非线性映射能力、良好的数据并行处理能力及容错能力，可以不涉及非线性函数的具体性质, 只要有足够训练样本组，就可以以任意精度逼近任意函数的特点，已在故障诊断[2]、预测[3]、函数逼近[4]、识别[5]等方面的应用中取得了显著的成效。但BP算法是基于梯度的算法，由于其理论缺陷，单独使用神经网络效果不是很理想[6]。在实际应用中，人们常将神经网络和小波变换[7]、遗传算法[8]、粒子群算法[9]及模糊控制[10]等相结合。2016年，新疆大学王雅等[11]利用变速箱齿轮磨损实验输入-输出数据，通过基于粒子群算法的RBF神经网络建立输出预测模型对齿轮磨损量进行预测。2017年，四川大学周丹等[10]将改进的粒子群算法、灰色模型和神经网络模型有机结合，构建了改进粒子群优化灰色神经网络预测模型对我国专利授权数量进行预测。2018年，华侨大学范伟等[12]提出遗传算法优化BP神经网络的压电陶瓷蠕变预测算法。

为了建立更加精确的预测模型，本文提出一种基于遗传退火算法优化的小波神经网络(GA-WNN)预测模型，其思路如下：首先通过用小波元对BP神经网络隐含层神经元的替换，建立小波神经网络；然后针对小波神经网络的初始权值、阈值、尺度因子、平移因子初始参数的优化问题，提出了采用遗传退火算法对其进行优化；最后利用已优化的网络初始参数进行网络训练，得到基于遗传退火算法优化的小波神经网络预测模型。进而，通过实例仿真，对模型进行了验证。

利用MATLAB开发出界面友好、使用方便的图形用户界面(GUI)以实现基于遗传退火的小波神经网络算法集成和交互可视化功能。 本文GUI设计中引入分层思想，将遗传退火算法优化模型参数设计为辅助GUI模块，由主模块GUI调用，每一层只专注自己需要实现的功能，实现高内聚，降低复杂度。

1 基于遗传退火优化的小波神经网络模型

1.1 构建小波神经网络模型

小波神经网络的思想是将常规神经网络隐含层的激励函数用小波基函数代替，利用误差函数极小化原理，不断调整网络的权值、阈值、小波基的平移、伸缩尺度因子从而增强函数逼近能力。研究表明：3层神经网络即可实现任意复杂的非线性映射问题，本文构造出来的3层小波神经网络结构如图1所示。

设输入层、隐含层及输出层的神经元个数分别为m、n、l，网络训练过程基于误差反向传播思想，按梯度下降方向调整权值、阈值及小波伸缩、平移尺度因子，具体步骤如下：

1) 信息的正向传播

输出层第i个神经元的输出为：

(1)

定义误差函数为：

(2)

图1 小波神经网络结构图

2) 基于误差的反向传播

各参数调整公式为：

(3)

其中η为学习率，负号表示梯度下降。

1.2 遗传退火算法优化网络模型初始参数

遗传退火算法克服了传统遗传算法优化神经网络初始参数过程中存在的收敛速度慢、计算的稳定性不好、容易陷入“早熟”收敛等问题。该结合算法能够丰富优化过程中的搜索行为，增强全局和局部的搜索能力和效率，进而在解空间中定位出一个较好的搜索空间，并将此作为其后采用小波神经网络搜索的初始权值。已知小波神经网络需要优化的初始参数集合为：

{w1kj，b1j，aj,τj，w2ji,b2i}

其中：k=1,2,…,m;j=1,2,…,n;i=1,2,…,l。则要优化变量个数N为：

N=m×n+3×n+n×l+l

(4)

故对小波神经网络初始参数优化问题转化为基于遗传退火算法的多参数优化问题，其主要步骤描述如下：

1) 参数设置，设定种群大小NIND、遗传代数MAXGEN、变量二进制位数PRECI、遗传算法的交叉概率PC、变异概率Pm、代沟GGAP、退火初始温度T0、温度衰减系数k，当前进化代数gen=1；

2) 编码并产生初始种群，对待优化的N个变量按顺序进行编码，并产生初始种群Sgen。本文采用二进制编码方式，即每1条染色体代表了1个网络的所有权值和阈值及尺度因子，用N维数组表示；

3) 适应度计算，利用适应度函数计算种群中个体i的适应度，以小波神经网络训练误差作为适应度函数，其公式为：

fit(i)=E

(5)

式中：fit为个体适应度函数；E为小波神经网络训练误差；i表示个体；

4) 选择操作产生下一代新的种群；

8) 终止条件判断，算法的迭代次数是否达到最大进化代数；

如果满足终止条件，则转向9)，算法结束；如果不满足终止条件，则gen=gen+1，转到4)。

9) 输出当前最优个体作为问题的最优解并将遗传退火算法搜索的最优个体解码, 赋值给小波神经网络权值、节点阈值、伸缩尺度因子及平移尺度因子。

1.3 GA-WNN网络模型训练过程

基于遗传退火算法优化的小波神经网络的算法流程如下：

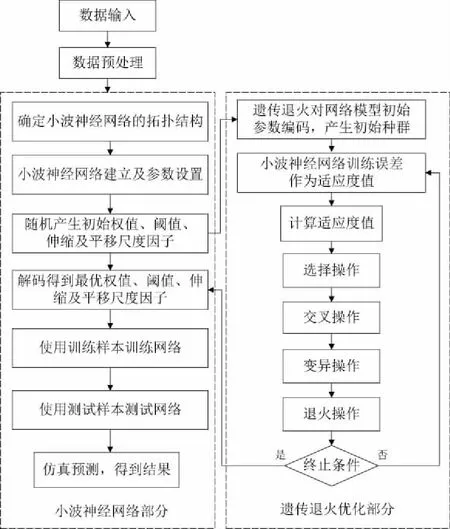
图2 基于遗传退火优化的小波神经网络算法流程图

主要步骤描述如下：

1) 样本数据输入及预处理；

2) 确定小波神经网络拓扑结构，本文采用3层小波神经网络结构，输入输出节点数由输入输出样本维度决定，设置隐含层节点数hiddenum；

3) 小波神经网络建立及网络参数设置，设置隐含层激励函数IH、输出层激励函数HO、学习函数LF、学习率η、最大训练次数Epochs及训练目标Goal；

4) 利用遗传退火算法优化小波神经网络的初始参数，具体过程包括：设定相应的参数,执行遗传退火操作，并由此得到进化解(最佳染色体个体)；

5) 解码并分解为网络所对应的优化权值、阈值、伸缩和平移尺度因子；

6) 将优化得到的权值、阈值、小波伸缩和平移尺度因子赋给小波神经网络，使用训练样本训练网格，按梯度下降方向调整网络参数并用测试样本测试网络；

7) 仿真预测得到结果。

1.4 GUI设计

为了实现整个建模过程的简便化，运用MATLAB/GUI工具开发了交互式基于遗传退火的小波神经网络预测仿真系统，该系统由数据导入与显示模块、遗传退火算法优化模型初始参数模块、仿真预测模块和结果保存模块4个部分，可以实现网络的建立、预测及仿真结果显示，如图3所示。其中遗传退火算法优化模型初始参数模块作为辅助模块通过点击主界面中“调用优化模块”按钮来调用，界面如图4所示。GUI的嵌套使用，使每一层只专注自己需要实现的功能实现高内聚，降低界面复杂度。

图3 基于遗传退火的小波神经网络预测仿真系统主界面

图4 遗传退火算法优化模型初始参数模块界面图

1) 数据导入与显示模块

依次点击“导入源数据”按钮、“数据预处理”按钮、“样本划分”按钮，完成数据的导入、导入数据归一化处理、训练样本及测试样本划分及样本数据显示。

2) 遗传退火算法优化模型初始参数模块

首先，点击主界面中“调用优化模块”按钮来调用遗传退火算法优化模型初始参数模块(辅助模块)。通过该辅助模块，合理设置种群大小、遗传代数等控制参数，依次点击“开始进化”按钮、“保存”按钮，实现对小波神经网络模型的初始权值、阈值、伸缩、平移因子初始值优化、优化结果的显示及保存；然后，点击“退出优化模块”按钮，退出该模块；最后，点击主界面上“显示”按钮，将优化的模型参数显示在主界面“初始参数显示”表格中。

3) 仿真预测模块

根据经验确定网络隐层节点数、合理选择各层激活函数及网络学习函数、设置训练次数及学习率等参数，即网络参数设置，点击主界面“预测模型”按钮进行仿真预测，同时实现网络预测结果图形显示。

4) 结果保存模块

依次点击“保存网络”按钮、“退出”按钮，完成网络保存、显示并退出系统。

2 算法应用实例

2.1 齿轮磨损预测模型建立

采用文献[11]中提供的实验输入-输出数据，以油温T、速度v、载荷P、时间t及振动信号(均值u、峰值P、峭度K及峰值指标Pc)为输入，齿轮磨损量Q为输出，利用上文研究的基于遗传退火小波神经网络建立预测模型。将试验监测数据前9组用于网络训练，后3组用于网络预测。GA-WNN网络参数设置见表1、表2。其中，小波神经网络模型参数设置如表1所示，遗传退火算法优化模型初始参数模块参数设置如表2所示。

表1 小波神经网络模型参数设置

表2 遗传退火算法优化模型初始参数模块参数设置

遗传退火算法优化小波神经网络初始参数过程如图5所示，从图中可以看出，种群的收敛速度快、计算的稳定性好， 在种群进化到第10代左右，已经找到最优解，第20代左右种群已趋于稳定。种群进化结束后将最优结果保存，作为小波神经网络初值。基于模拟退火的小波神经网络仿真预测得到结果如图6所示，可以看出，预测曲线与原始曲线非常接近。

图5 遗传退火算法优化小波神经网络初始参数

图6 预测模型仿真图

2.2 误差分析

为了定量比较各预测模型预测效果，定义4个误差评价指标，见式(6)。

(6)

基于遗传退火小波神经网络(GA-WNN)误差评价指标如表3所示。

表3 基于遗传退火小波神经网络(GA-WNN)误差评价表

文献[11]中通过式(6)的指标比较了AR模型、BP神经网络模型、Hermite神经网络及基于粒子群算法的RBF神经网络,其误差评价指标如表4所示。

表4 不同网络模型误差评价表

通过比较表3、表4可以看出，本文提出的算法模型(GA-WNN)上述4个误差评价指标均优于AR、BP、Hermite、RBF预测模型，故本文提出的GA-WNN算法预测模型具有更小偏差、更小波动、更稳定，适用于复杂的齿轮磨损量预测。

3 结语

本文建立的基于遗传退火优化小波神经网络预测模型(GA-WNN)结合了小波神经网络强大的非线性预测能力和遗传退火算法的全局优化搜索功能，与传统的AR模型、BP神经网络模型、Hermite神经网络及基于粒子群算法的RBF神经网络预测相比，具有较高的预测精度、波动小、更稳定，适用于复杂的预测问题。 此外，互动式界面开发，完成实验输入数据的自动化读取、参数的个性化设定以及输出结果的快速可视化。用户只需通过操作界面，即可训练出适应不同要求的网络模型，为用户快速获取适用于不同问题的预测模型提供了便利。