基于RBF的主动悬架反演滑模控制策略研究*

李雅琦，李 伟，陈应鹏，郑 柱

(重庆交通大学 机电与车辆工程学院，重庆 400074)

0 引 言

主动悬架是一种将置于悬架系统轴线上的主动力发生器连续控制车体垂直运动[1]的技术。与半主动悬架系统相比，全主动悬架灵活性更强，并能够抑制不规则道路引起的车体振动。

由于悬架系统的高度非线性特征，如何更好地对其控制研究是国内外的研究热点。汪洪波等人[2]针设计了一种可拓主动悬架控制器，并优化可拓系数来提高控制性能；周兵等人[3]针对悬架系统，将综合控制与控制效果进行了对比，结果表明，综合的鲁棒稳定性更好；周辰宇等人[4]构建了悬架系统的线性滤波反演控制器，实现了均衡控制；庞辉等人[5]通过对悬架系统进行了动力学分析，提出了T-S模糊控制方法和悬架系统非线性动力学模型，达到了改善悬架系统的综合性能的目的；陈士安等人[6-7]在滑模控制的基础上增加了全息最优控制方法，经过实验证明，全息最优滑模控制具有很好的鲁棒性。

本文对悬架系统引入滑模控制，并将反演控制与之相结合，同时利用神经网络的逼近能力，提出一种改进型径向基(RBF)函数反演滑模控制策略。

1 主动悬架系统控制模型

1.1 二自由度主动悬架系统模型

在全主动悬架系统中，由作动器代替被动悬架中的弹簧和减振器。为了降低能量消耗，笔者将悬架弹簧与作动器并联，以支持车身静载荷[8]。由于主动悬架系统存在不确定性，1/4车辆模型结构简单，便于研究各项影响指标响应变化。

2自由度1/4车辆模型如图1所示。

图1 2自由度1/4车辆模型

为了保证被控悬架得到更好的动态响应和优化控制，应满足如下条件：

(1)车身结构为刚性，且悬架结构不超过机械结构的最大值，即：

(1)

(2)车辆作匀速直线运动，且车轮动载荷不超过机械结构动载荷的限值，即：

|k1(x1-x0)|≤(m1+m2)g

(2)

式中：g—重力加速度，g=9.8 m/s2。

根据2自由度模型，可得系统动力学方程：

(3)

1.2 主动悬架系统运动状态模型

系统的状态方程设计如下：

(4)

2 RBF控制策略

滑模控制具有算法简单、灵敏度高、鲁棒性好等优点[9]；Backstepping法(反演法)既考虑控制率和自适应率，又能满足闭环系统的动静态稳定性。将滑模控制与反演法相结合，既能满足鲁棒性要求，又能降低抖振。

2.1 自适应反演滑模控制策略

首先定义误差为：

ei=xi-αi-1

(5)

e1=x1-xd

(6)

式中：xd—位置指令。

(1)第一步。定义虚拟控制量：

(7)

式中：c1—设计参数。

得到第1个误差子系统动态方程：

(8)

选择Lyapunov函数：

(9)

定义切换函数：

(10)

(2)第二步。第2个误差子系统的动态方程为：

(11)

定义滑模面为：

s=b1e1+e2(b>0)

(12)

式中:b—滑模面上的收敛速度。

(13)

设计控制率为：

u=ueq+uvss

(14)

式中：ueq—等效控制率；uvss—切换控制率。

(15)

定义切换控制率为:

(16)

定义估计误差为：

(17)

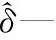
(18)

式中：r—设计参数。

2.2 基于RBF自适应反演滑模控制策略

径向基神经网络(RBF)是一种三层前馈网络，拥有强大的逼近能力、学习能力和分类能力，对任意精度的任意连续函数都能够逼近[10]。将径向基神经网络引入反演滑模控制策略，能够使控制系统实现模型未知部分的自适应逼近，同时可调节整个闭环系统的稳定性和收敛性。

引入RBF神经网络算法：

(19)

f=W*h(x)+ε

(20)

式中：x—网络输入；j—网络隐含层第j个节点；W*—网络理想权值；ε—网络的逼近误差。

设计RBF等效控制率为：

(21)

定义滑模面为：

(22)

满足狄利克雷条件，RBF神经网络可表示为：

(23)

(24)

(25)

(26)

(27)

那么式(23)可写为：

(28)

其中：

εP=εG+εH+εI+εJ+εd

(29)

(30)

2.3 稳定性分析

选定Lyapunov函数：

(31)

式中：QG,QH,QI,QJ,Qd—正定矩阵。

可得：

(32)

(33)

可简化为：

(34)

3 改进型控制策略验证

3.1 路面输入模型

C级路面随机激励图如图2所示。

图2 C级路面随机激励图

路面位移不平度的表达式为：

(35)

式中：f0—滤波器下限的截止频率；Gq(n0)—空间频率功率谱密度；n0—参考空间频率；u—车速；q(t)—白噪音；ω(t)—高斯分布白噪音。

3.2 仿真结果

动态性能指标的均方根值如表1所示。

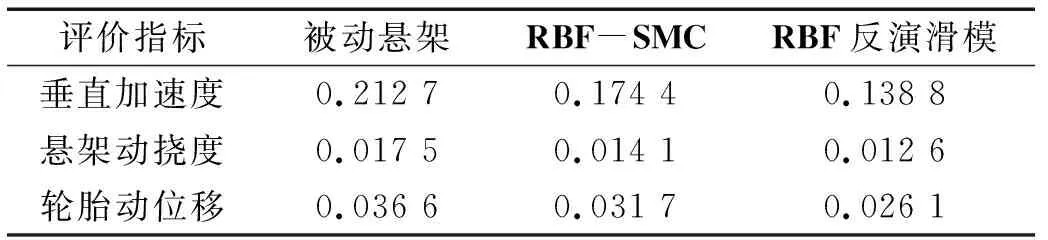
表1 动态性能指标的均方根值

车身加速度响应曲线如图3所示。

图3 车身加速度响应曲线

图3即为使用本文所提的控制策略与RBF-SMC控制策略后，被动悬架的车身垂直加速度响应曲线对比图。

由图3可知：在使用本文方法控制下的车身加速度降低了34.7%(与被动悬架相比)，使用RBF-SMC控制策略降低了18%(与被动悬架相比)。

悬架动挠度响应曲线如图4所示。

图4 悬架动挠度响应曲线

图4即为使用本文所提的控制策略与RBF-SMC控制策略后，被动悬架的悬架动挠度响应曲线对比图。车身受到路面冲击时会发生上、下振动，悬架动挠度与车身振动程度呈正相关。

由图4可知：使用本文控制策略下的悬架动挠度降低了28%(与被动悬架相比)，使用RBF-SMC控制策略能降低了19.4%(与被动悬架相比)。

轮胎动位移响应曲线如图5所示。

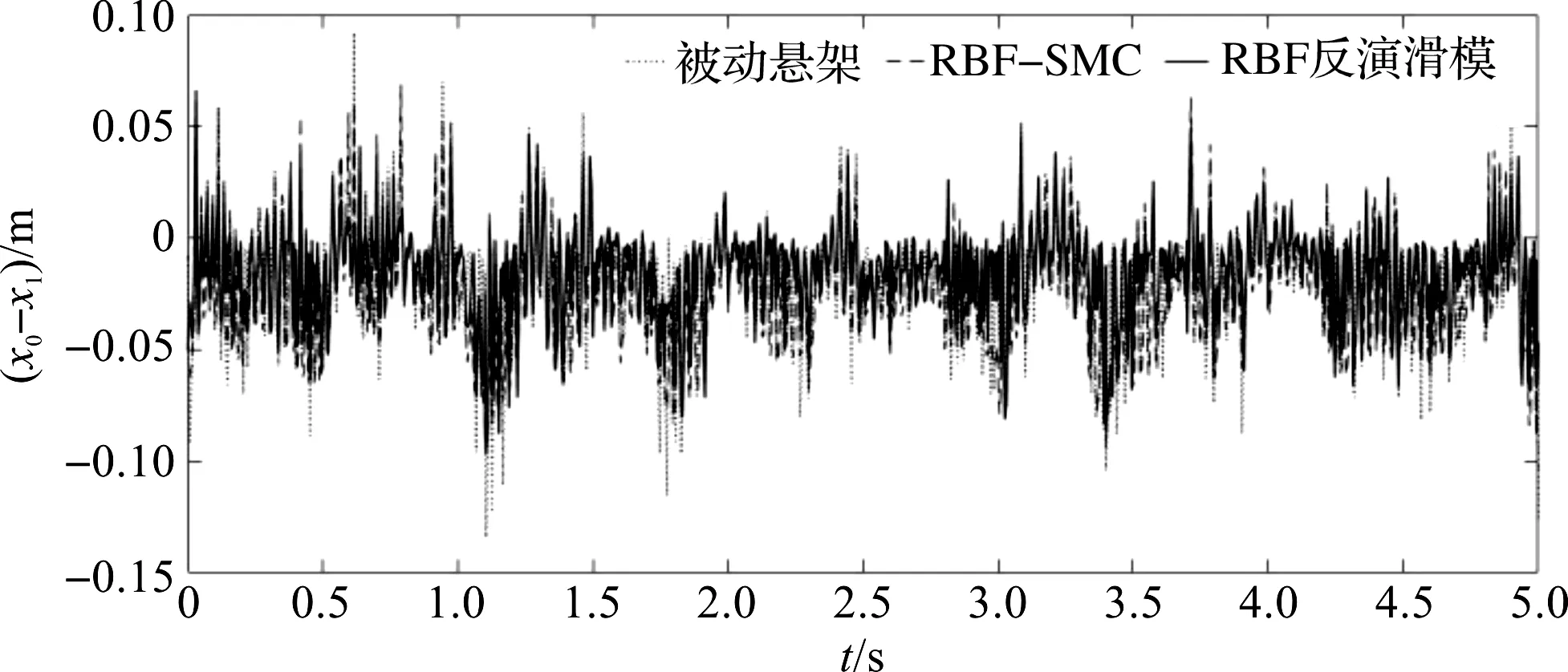
图5 轮胎动位移响应曲线

图5即为使用本文所提的控制策略与RBF-SMC控制策略后，被动悬架的车轮动位移响应曲线对比图。

由图5可以看出：使用本文所提的控制策略下的悬架动挠度降低了28.7%(与被动悬架相比)，使用RBF-SMC控制策略能降低了13.4%(与被动悬架相比)。

4 结束语

以1/4汽车悬架系统为研究对象，笔者将径向基神经网络(RBF)算法引入自适应反演滑模控制策略，在C级路面上通过滤波白噪声激励，对径向基神经网络反演滑模控制策略进行了验证；

通过仿真验证表明：本文设计的控制策略使振动中悬架垂直加速度、悬架动行程、轮胎动位移明显降低，系统的动态性能和稳定性得到改善，提升了悬架系统的控制性能。

参考文献(References):

[1] TOROYAN T, PEDEN M M, IAYCH K. Global status report on road safety 2015[J]. Inj Prev, 2013,15(4):286.

[2] 汪洪波,林 澍,孙晓文,等.基于可拓理论的汽车主动悬架系统H∞控制与优化[J].汽车工程,2016,38(11):1382-1390.

[3] 周 兵,吴晓建,文桂林,等.基于μ综合的整车主动悬架鲁棒控制研究[J].振动工程学报,2017,30(6):1029-1037.

[4] 周辰雨,余 强,张 凯.基于滤波技术的非线性Backstepping主动悬架控制[J].长安大学学报：自然科学版，2017,37(2):115-126.

[5] 庞 辉,陈嘉楠,刘 凯.汽车磁流变半主动悬架系统自适应反推跟踪控制[J].兵工学报,2017,38(7):1430-1442.

[6] 陈士安,祖广浩,姚 明,等.磁流变半主动悬架的泰勒级数-LQG时滞补偿控制方法[J].振动与冲击,2017,36(8):190-196，243.

[7] 陈士安,王骏骋,姚 明.车辆半主动悬架全息最优滑模控制器设计方法[J].交通运输工程学报,2016,16(3):72-83，99.

[8] 寇发荣,许家楠,刘大鹏,等.电动静液压主动悬架双滑模控制研究[J].中国机械工程,2019,30(5):542-548，553.

[9] 秦 斌,张俊杰,王 欣,等.基于RBF网络的车载超级电容滑模控制系统[J].电气传动,2018,48(8):65-69.

[10] 李文顶,施光林.电液伺服系统RBF神经网络滑模控制[J].液压与气动,2019(2):109-114.