新型无耦合两转动并联机构运动学及性能分析*

王科明，张彦斌，荆献领，陈子豪，芦风林

(河南科技大学 机电工程学院，河南 洛阳 471003)

0 引 言

按照其动平台输出运动特性的不同，并联机构可分为纯移动[1]、纯转动[2]和混合型[3]三种机构。纯转动并联机构的动平台具有2个或3个转动自由度。其中，两自由度转动并联机构在卫星天线、踝关节康复机器人等领域中具有独特的优势，已成为该领域研究的热点问题[4-5]。按输入与输出之间的关系，并联机构又可分为耦合和解耦两种机构[6]。其中，解耦并联机构因在运动和控制等方面呈现出来的优越性，受到了国内外学者的广泛关注[7-8]。

宋轶民等[9]提出了一种具有大转角的两转动并联机构，对其进行了构型分析和运动学优化设计；XU等[10]通过分析机构分支约束力螺旋的几何关系，设计了一类具有连续转轴的两转动并联机构；DUAN等设计了两自由度球面并联机构，并对其进行运动规划和动力学分析，得出了机构的输入和输出之间的角位移、角速度和角加速度的定量关系；CARRICATO等[11]通过减少机构中闭环的数目，设计出了一种含有单环回路的并联手腕机构，增大了机构的工作空间；侯雨雷等[12]针对并联机构内部耦合性所带来的一些问题，提出了一种新型的两自由度转动解耦并联机构，并讨论了驱动输入的选择对机构奇异性的影响。

本文将提出一种新型无耦合RR-RUPU两转动并联机构，详细分析机构的运动学、奇异性，利用运动条件指标对机构进行完全各向同性设计，并进行运动学仿真分析。

1 机构的结构设计与输出特性分析

新型RR-RUPU并联机构的结构简图如图1所示。

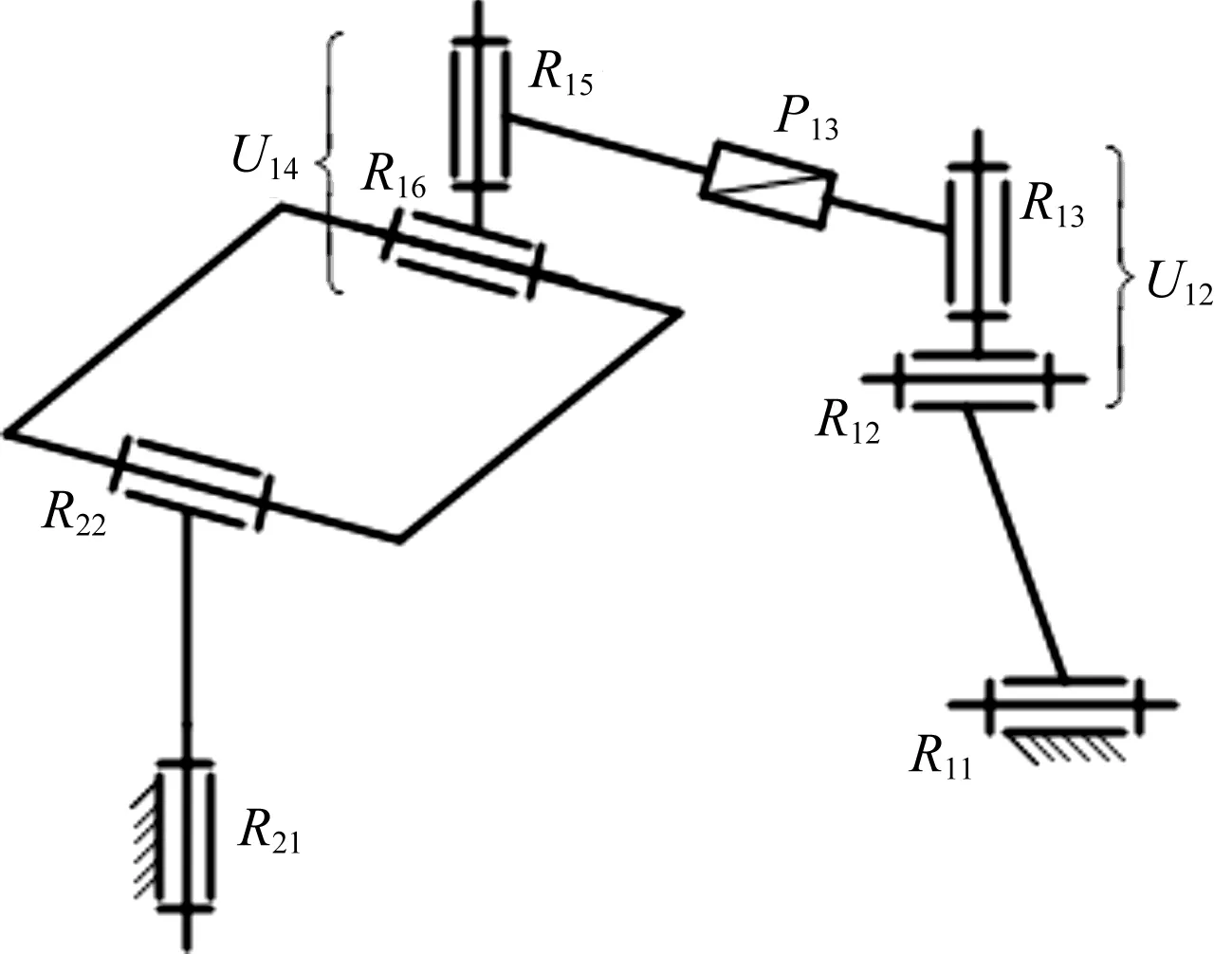
图1 新型RR-RUPU并联机构简图

图1中：该机构由动平台、定平台以及连接两平台的两条单开链组成[13]。第一条分支从定平台到动平台的布置依次为转动副R11、万向铰U12、移动副P13、万向铰U14。

为便于结构描述和问题分析，将U12副与U14副分别用两个轴线垂直相交的转动副R12与R13、转动副R15与R16代替。第一条分支运动链中R11与R12副的轴线相互平行，R13与R15副的轴线相互平行且垂直于P13副的移动方向，因此，该分支运动链的拓扑结构可记为SOC{-R11//R12⊥R13(⊥R13)//R15⊥R16-}。第二条分支从定平台到动平台运动副的布置依次为转动副R21和R22，两运动副轴线垂直相交，该分支的拓扑结构记为SOC{-R21⊥R22-}。

两条分支装配条件为：与定平台相连的转动副R11和R21的轴线相互垂直；与动平台相连接的转动副R16和R22的轴线相互平行。选取安装于定平台上的R11和R21副作为机构的主动副。

根据机构运动副的配置关系，可写出第一条分支和第二条分支的方位特征集Mb1和Mb2，分别为：

(1)

(2)

其中，符号右上标数字表示支链的特征自由度数，如r2//(R15,R16)表示第一条分支末端构件在平行于R15和R16副轴线所确定的平面上，存在2个转动自由度，t0表示移动自由度的数目为0。

因此，图1所示机构动平台的方位特征集Mb为：

(3)

由式(3)可知：动平台具有绕R21副和R22副轴线转动的自由度，即输出特性为二维转动，而不存在移动自由度。

并联机构自由度M可利用Yang-Sun公式进行计算，即：

(4)

式中：g—机构运动副总数；fk—第k个运动副的自由度数；v—独立回路数。

对于图1所示机构，g=6，∑fk=8，v=1，∑ξLm=6，因此M=2。可见计算结果与前述分析一致，所以该机构只能实现空间二自由度转动。

2 运动学分析

2.1 姿态分析

在RR-RUPU并联机构的三维CAD模型中，定坐标系O-xyz，其原点O位于第二条分支两转动副轴线的交点，z轴与R21副轴线重合，x轴平行于R11副轴线；动坐标系P-uvw，其原点P位于动平台上且与定坐标系的原点O重合，v轴与R22副轴线重合，w轴垂直于动平台平面。

在初始位形下，两坐标系的轴线分别对应重合。设q11和q21分别为两主动副的输入角位移；α为动平台绕v轴转动的姿态角，设其绕v轴的反方向转动为正；β为动平台绕z轴转动的姿态角，绕z轴方向转动为正；l为第一条分支主动杆的长度，即R11和R12副轴线间的距离；r表示动平台结构尺寸，即R16和R22副轴线间距离。

建立局部坐标系O1-x1y1z1，其原点O1位于转动副R11的轴线上，且x1轴与该轴线重合，z1轴垂直定平台平面。

新型RR-RUPU并联机构CAD模型如图2所示。

图2 新型RR-RUPU并联机构CAD模型

故第一条分支运动链在局部坐标系O1-x1y1z1下的运动螺旋系为：

(5)

式中：Lij，Mij，Pij，Qij，Rij—非零常数(i=1，j=1,4,5,6)。

根据式(5)可知：第一条分支运动链的运动螺旋系为6系，因此不存在反螺旋。

而在定坐标系O-xyz下，第二条分支运动链的运动螺旋系为：

(6)

同理可得，该螺旋系为2系，反螺旋为4系，即：

(7)

(8)

(9)

纯转动RR-RUPU并联机构的姿态正解，是指已知主动关节的输入角位移(q11,q21)，求其动平台的姿态角(α,β)。图2中，A点为U12副中两转轴轴线的交点，B点为P13副移动方向与U12副竖直转轴轴线的交点，C点为P13副的移动方向与U14副竖直转轴的交点，D点为U14副中两转轴的交点。

(10)

(11)

将式(11)进一步整理，可得：

rsinα=O1z+lsinq11+a+b

(12)

由于O1z、a、b仅与机构的结构尺寸有关，只需适当设计其结构尺寸，便可满足O1z+a+b=0成立，那么式(12)可化简为：

rsinα=lsinq11

(13)

从而可求得动平台姿态角α为：

(14)

由图2可知，动平台绕z轴的姿态角β仅与第二条分支主动副R21的角位移q21相关，故两者的关系可写为：

q21=β+c0

(15)

式中：c0—动平台绕z轴的初始角度。

由于前面定义了动坐标系在初始位置时与定坐标系重合，即c0=0，则式(15)可改写为：

β=q21

(16)

2.2 角速度分析

将式(13，16)对时间进行一阶求导，可得到该机构的角速度方程，即:

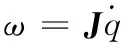
(17)

且有：

(18)

根据式(18)可知：速度雅可比矩阵为对角阵，主动关节的输入速度与动平台的输出速度之间存在一对一的控制映射关系，所以该机构具有无耦合的运动学特性，尤其是雅可比矩阵对角线上的第二个元素等于1。

3 奇异性分析

奇异性是并联机构的固有属性，在机构的设计过程中，奇异性分析是必不可少的环节。FANG和TSAI[14]将并联机构的奇异类型分为：分支运动奇异、驱动奇异和约束奇异3种类型。

3.1 分支运动奇异

这种运动奇异的发生与并联机构分支运动链的运动螺旋系的阶数有关，故称为分支运动奇异。当运动螺旋系的阶数发生改变时，动平台的约束螺旋系的阶数也随之改变，导致机构动平台会瞬间得到或失去一个或几个自由度。

由式(6)可知：第二条分支的运动螺旋系始终为2系，故该分支不会发生分支运动奇异形式。而式(5)表明，第一条分支的运动螺旋系为6系螺旋，该螺旋系的相关性可等价于由该螺旋系构成的阶方阵A是否满秩，即：

(19)

若矩阵A不满秩，则该运动螺旋系线性相关，此时其行列式的值det(A)为0。

由于矩阵初等变换不影响矩阵的秩，即不影响其行列式是否为0。根据矩阵分块计算方法，当仅考虑A对应行列式的值是否为0时，则有：

det(A)=det(E)det(F)

(20)

其中：

若矩阵E或F其中一个不满秩，那么矩阵A便不满秩。下面对两种类型分别进行分析：

(1)类型1：矩阵E不满秩。

经计算det(E)=lcosq11cosβ，那么det(E)=0成立的条件为β=±π/2或q11=±π/2。

当q11=±π/2时，将其代入式(5)可得该位形下的运动螺旋系，同时可求得该位形处分支的约束螺旋为：

(21)

(2)类型2：矩阵F不满秩。

根据式(20)可得矩阵F行列式的值为：

det(F)=M14lcosq11

(22)

由于结构的限制，在图2所示的装配位形下，当β=-π/2和q11=-π/2时，机构不会发生分支奇异。

分支奇异位形如图3所示。

图3 分支奇异位形

3.2 驱动奇异

(23)

(24)

式中：Q=-(cosβ+lcosq11sinβ)/R16。

将式(23，24)整理成矩阵的形式，即：

(25)

将矩阵分块后可知，当且仅当矩阵G主对角线上的第二个子块不满秩时，矩阵G不满秩。即当时矩阵欠秩，从而约束力螺旋系线性相关，那么便有4组奇异位形组合，分别为：β=π/2,q11=π/2；β=-π/2,q11=π/2；β=π/2,q11=-π/2；β=-π/2,q11=-π/2。

由于机构的结构限制，在图2所示的装配位形下，组合c、d不会发生。

当R11副被锁定后，该分支对动平台的驱动力螺旋与第二条分支产生的约束力螺旋线性相关，从而产生驱动奇异位形，如图4所示。

图4 驱动奇异位形

3.3 约束奇异

分支施加到动平台的约束力螺旋线性相关时，动平台得不到应有的约束力，产生非预期自由度，即发生约束奇异。

由式(7)可知：在图2所示机构的装配位形下，分支施加到动平台上的约束力螺旋系始终包含3个线性独立的约束线力螺旋和一个约束力偶螺旋，因此，该机构不存在约束奇异。

4 机构的完全各向同性设计

在整个工作空间内，若机构的雅可比矩阵条件数恒等于1，则称该机构具有完全各向同性的运动学性能。由于这类机构的雅可比矩阵为单位阵，其输入-输出速度之间的运动传递既不放大也不缩小，更不存在失真情况，可见完全各向同性并联机构具有良好的运动和力传递性能。

通常采用机构的运动条件指标(KCI)来表征机构的灵巧性。当KCI=1时，机构具有各向同性的特性。KCI在数值上等于雅可比矩阵J的条件数k(J)的倒数，即：

(26)

式中：σmax—J的最大奇异值；σmin—J的最小奇异值。

对于无耦合并联机构，其速度雅可比矩阵为对角矩阵即正规矩阵，因此，对于式(18)所示的雅可比矩阵J，存在一个阶的酉矩阵U，使得：

(27)

(28)

式中：λ1，λ2—矩阵J的特征值；UH—U的共轭转置矩阵；JH—J的共轭转置矩阵。

由于KCI的V值在区间[0,1]内变化，将雅可比矩阵J的奇异值代入式(26)可得：

(29)

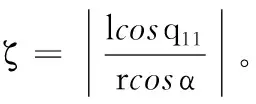
因此，KCI值的大小不仅与机构的结构尺寸有关，还与机构输入角位移q11以及输出角位移α有关。

对于给定的机构，其结构尺寸也随之确定。将式(14)进行三角变换，并代入ζ的表达式可得：

(30)

式中：κ=l/r。

机构运动条件指标KCI随其结构参数κ和输入角位移q11变化的规律如图5所示。

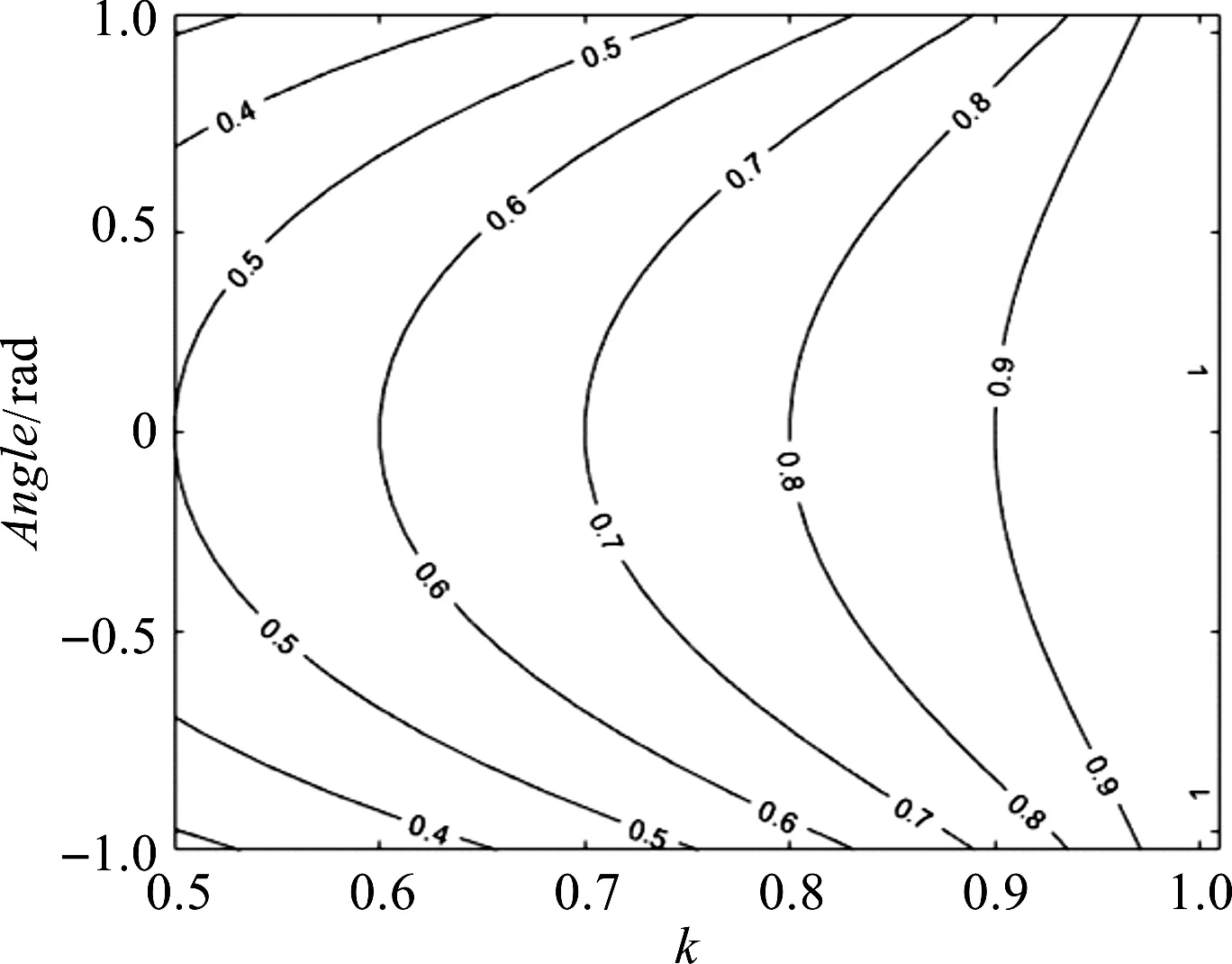
图5 运动条件指标的等值线图

由图5可知：KCI等值线关于直线q11=0°对称分布，且随着结构参数κ值的增大趋于平缓；值得注意的是，当κ=1时，无论q11如何变化，KCI的值为常数且恒等于1。

将κ=1代入式(28)可得KCI=1，验证了图5中KCI等值线的变化规律。由此可见，只要满足结构尺寸条件l=r，则机构在整个工作空间内具有完全各向同性的运动学性能。

5 机构运动学仿真分析

运动学仿真的主要目的是直观再现机构输入与输出之间的映射关系。ADAMS/View中提供了丰富的几何体建模工具，但其对复杂形状零件的建模功能相对薄弱，难以用其来创建具有复杂特征的零件；而相对于ADAMS/View的运动学分析，SolidWorks/motion运动分析模块的通用性和准确度较差，因此，本文采用SolidWorks和ADAMS软件的运动学联合仿真的方式，对RR-RURU并联机器人机构进行运动学虚拟样机的建模和仿真。

设定机构的结构尺寸为l=r，基于SolidWorks软件，对机构进行建模。笔者将模型数据文件导入ADAMS软件，并对导入的三维实体模型重新定义各构件的约束关系，完成虚拟样机的创建；设置两主动关节的角位移函数分别为：q11=30°sin(πt/6)，q21=-25°sin(πt/4-π/3)，将其编译到ADAMS的驱动函数中，设置仿真时间为12 s，仿真步数为200。

在ADAMS/Postprocessor模块中得到的动平台的运动学仿真曲线如图6所示。

图6 动平台的运动学仿真曲线

根据图6的运动学仿真结果可知：在整个运动过程中，动平台的角位移和角速度可在一定范围内变化，运动过程平稳，不存在剧烈冲击的现象。

6 结束语

针对并联机构的强运动学耦合性问题，本文设计出了一种新型RR-RUPU两转动并联机构，推导出了其姿态和角速度方程；由于其速度雅可比矩阵为对角阵，其具有无耦合运动学特性，即其主动关节的输入速度与其动平台的输出速度之间具有一对一的控制映射关系，所以该机构具有良好的运动传递性能。尤其是当结构尺寸满足一定的要求情况下，其雅可比矩阵为单位阵，机构具有完全各向同性的运动学性能。

笔者所作的研究为该机构的动力学及其实体样机的研制提供了一定的理论基础。

参考文献(References):

[1] ZHANG Y B, ZHAO Y F, JING X L, et al. Type synthesis of uncoupled translational parallel manipulators based on actuation wrench screw theory[J]. Advances in Mechanical Engineering, 2018,10(1):1-10.

[2] HOU Y L, DUAN Y B, YAO J T, et al. Configuration optimization and static analysis of adjusting parallel mechanism for the sub-reflector of antenna[J]. Advanced Materials Research,2011(338):425-430.

[3] 马广英,陈 原,姚云龙,等.一种水陆两栖机器人的两移两转串并混联腿机构[J].哈尔滨工程大学学报,2018,39(1):135-142.

[4] LALIBERTÉ T, GOSSELIN C. Synthesis, optimization and experimental validation of reactionless two-DOF parallel mechanisms using counter-mechanisms[J]. Meccanica,2016,51(12):3211-3225.

[5] DUAN X, YANG Y, CHENG B. Modeling and analysis of a 2-DOF spherical parallel manipulator[J]. Sensors,2016,16(9):1485.

[6] 刘 晓,赵铁石,边 辉,等.耦合型3自由度并联稳定平台机构动力学分析[J].机械工程学报,2013,49(1):45-52.

[7] ZENG D X, HUANG Z. Type synthesis of the rotational decoupled parallel mechanism based on screw theory[J]. Science China Technological Sciences, 2011,54(4):998-1004.

[8] 张彦斌,荆献领,韩建海,等.无耦合二自由度转动并联机构型综合方法研究[J].机械工程学报,2018,54(15):21-30.

[9] 宋轶民,周 培,齐 杨，等.一类大转角两转动并联机构的构型分析与运动学优化设计[J].天津大学学报,2019,52(9):908-916.

[10] XU Y D, ZHANG D S, WANG M, et al. Type synthesis of two-degrees-of-freedom rotational parallel mechanism with two continuous rotational axes[J]. Chinese Journal of Mechanical Engineering, 2016,29(4):1-9.

[11] DI G R. Single-loop wrists which generate triangular structures[J]. Mechanism & Machine Theory, 2014,80(80):230-245.

[12] 侯雨雷,张占叶,胡鑫喆,等.新型两转动自由度完全解耦并联机构及其特性[J].哈尔滨工业大学学报,2014,(9):80-85.

[13] 安明云,于大泳,张黎明,六自由度并联机构的误差分布研究[J].轻工机械,2019,37(1):29-33.

[14] FANG Y F, TSAI L W. Structure synthesis of a class of 4-DoF and 5-DoF parallel manipulators with identical limb structures[J]. International Journal of Robotics Research, 2002,21(9):799-810.