第三轨受流器滑板螺栓联接残余预紧力特性研究*

姚齐水，袁秋炜，陈 章，余江鸿*

(1.湖南工业大学 机械工程学院，湖南 株洲 412007；2.中车株洲电力机车有限公司，湖南 株洲 412001)

0 引 言

受流器是列车从第三轨(供电轨)取流满足列车电力需求的受流设备，其稳定性对于第三轨供电列车的安全行驶显得至关重要。受流器的受流滑板与滑板支架通过螺栓联接紧固。在列车行驶过程中，受流器受到车辆随机振动、与第三轨接触碰撞等振动激励，易造成螺栓联接松脱，影响受流稳定性和列车行驶安全性。因此，研究受流器滑板螺栓联接在列车运行时的松驰机理具要重要意义。

关于受流器与第三轨的碰撞特性问题，郎鹏[1]以“下接触式受流系统”为研究对象，建立了合理简化的受流器/三轨弯头碰撞模型，研究了不同参数对受流系统在第三轨弯头处的接触碰撞影响规律，并基于碰撞模型对三轨弯头的几何形状进行了优化；关于受流器与第三轨的接触振动特性问题，王文娇[2]对下接触式受流系统与第三轨端部弯头接触时的垂向振动特性进行了研究，分析了运行速度提升对受流系统垂向振动特性的影响；关于振动工况下螺栓松弛的问题，JUNKER等[3]设计了试验机，研究了横向载荷作用下螺栓的松弛情况，发现横向载荷更易引起螺栓联接的松弛；NASSAR等[4-5]对不同的弹塑性模型，施加了轴向载荷，得出了螺栓残余预紧力在初期下降明显且不可恢复的结论；YANG X等[6-8]以解析模型解释了螺栓联接自松弛现象，并以实验进行了验证；刘建华[9]基于螺栓松动实验装置，通过施加轴向激励，研究了不同涂层对于螺栓联接防松性能的影响；王传华等[10]建立了精确的仿真模型，通过与实验的对比，研究了螺栓扭转变形对其松动的影响；刘传波[11]通过横向振动实验，分析了各因素对防松性能的影响程度，为螺母的选择提供了参考。

总体来说，国内外学者对受流器及其螺栓联接的振动和松驰从碰撞特性、横向载荷和轴向载荷等角度进行了大量研究。

在此基础上，基于受流器使用的实际工况，笔者研究列车运行时受流器滑板螺栓联接残余预紧力特性，对第三轨受流器滑板螺栓联接松驰机理的研究形成有益补充，为提高其防松性能提供参考。

1 基于轨道不平顺谱的列车运行速度分析

1.1 受流器与第三轨接触有限元模型

第三轨受流器主要由滑板、滑板支架、摆臂、扭簧、弾性轴、安装座、熔断器箱和相关线路组成。

为便于细节参数的设置，并不影响分析结果且能提高分析效率，笔者分别建立受流器与第三轨接触有限元模型和螺栓联接模型进行分析；对于受流器与第三轨有限元模型，根据实际参数进行建模，并将扭簧简化为转动面的扭转联接。

由此笔者在CREO软件中进行三维建模，并将其导入ABAQUS中进行参数设置。

其有限元模型如图1所示。

图1 受流器与第三轨接触有限元模型

1.2 轨道不平顺谱的数值模拟

受流器与第三轨接触，在列车运行的时候所受到振动条件较为复杂，如来自车轨、列车的各种振动和受流滑板与第三轨的碰撞等。轨道不平顺是车轨振动的主要原因，是研究车辆与轨道相互作用的基础。轨道不平顺谱，记录轨道不平顺，由功率谱密度函数描述，需要通过Matlab进行时频转换为时域函数。

笔者选用美国五级谱为轨道不平顺谱，通过Matlab编程转换，得到不同速度的轨道不平顺时间位移曲线。

1.3 模型设置

笔者给安装座的下表面施加由1.2得出的轨道不平顺时间位移曲线；给安装座的侧面施加不同的速度，并进行仿真分析。

1.4 仿真结果

不同速度运行下，受流滑板与第三轨接触力的变化曲线如图2所示。

图2 不同速度下，接触力平均值

由图2可知：当速度为50 km/h和60 km/h，接触力相较于30 km/h、40 km/h和70 km/h有所下降。这说明列车运行时速为50 km/h到60 km/h时，接触性能最佳，有利于受流的稳定性。

2 螺栓联接模型的建立及验证

2.1 有限元模型

第三轨受流器滑板通过螺栓与滑板支架联接。受流器滑板螺栓对称分布，由于只考虑滑板上的螺栓联接，可只取其中一个螺栓联接作为研究对象。

基于实际情况，笔者选用M10×1.5三角形螺纹螺栓联接，用CREO建立三维模型。

其基本参数如表1所示。

表1 螺栓联接模型的基本参数

螺栓联接仿真模型中，螺栓材料选用高强度钢，屈服极限为640 MPa；滑板材料选用Q235钢，屈服极限为235 MPa。

螺栓联接有限元模型如图3所示。

图3 螺栓联接有限元模型

2.2 模型设置

笔者在螺栓头部承压面、螺母承压面、滑板接触面、螺纹啮合面处设置接触对；各接触面的摩擦系数均设为0.1。

在螺栓杆中间部位施加预紧力单元，并固定其长度，以保持预紧力大小。基于实际工况，笔者对上滑板的上表面施加全约束，对上滑板与坐标面YOZ平行的两个侧面进行X方向约束，对上滑板与坐标面YOX平行的两个侧面进行Z方向的约束；对滑板与坐标面YOZ平行的两个侧面进行X方向约束。

2.3 初始预紧力工况下的模型验证

Yamamoto方法[12]能较全面地分析螺纹牙的轴向力受力情况。

将螺纹牙视作梁结构，忽略螺纹升角，可将应变变形分为5种类型：螺纹牙受弯曲及剪切产生的变形δ1和δ2、牙根倾斜产生的变形δ3、牙根受剪切产生的变形δ4及螺栓螺母径向变形δ5，其公式分别如下：

(1)

(2)

(3)

(4)

(5)

(6)

式中：E—弹性模量；v—材料的泊松比；f—垂直于螺纹面的力；α—牙侧角；δ5b—外螺纹啮合面的轴向变形；δ5n—内螺纹啮合面的轴向变形。

对于三角形螺纹，a=0.888p，b=0.5p，c=0.289p。将外螺纹、内螺纹的变形累积，可得：

(7)

(8)

根据各变形之间的关系，以及螺栓轴向力与螺栓伸长量、螺母压缩量之间的关系，可得出：

(9)

其中：

(10)

式中：Fa—X位置处螺纹截面的轴力；X—螺纹截面到螺母承压面的距离；Fn—螺母承压面的轴力，可等同于螺栓初始预紧力；λ—载荷分布特征参数；L—螺栓与螺母的啮合长度；β—螺纹升角。

将螺栓联接的参数代入式(10)，可得出λ为0.048 57。根据式(9)，可计算出各层螺纹轴力。

通过有限元法和Yamamoto法计算的螺纹截面轴力如图4所示。

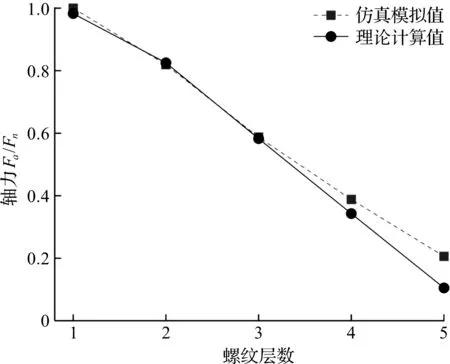
图4 螺纹截面轴力

从图4可以看出：仿真模拟值与理论计算值在靠近螺母承压面的三层螺纹上重合度高，但在后两层螺纹上存在着一定偏差。这是由于Yamamoto法忽略了螺纹升角，未考虑带螺升角螺纹在层与层之间负载连续性上的影响，在远离螺母承压面上螺纹的轴力出现一定偏差。

2.4 振动载荷设置

目前对于螺栓振动特性的研究中，所受到的振动载荷基本上都是正弦载荷[13-14]。由于笔者所讨论的是第三轨受流器滑板螺栓，所受到的实际载荷与正弦载荷不相符合；以1.4仿真结果提取的数据，作为精确建模的螺栓联接的振动载荷。

笔者对下滑板与坐标面YOZ平行的两个侧面进行X方向约束；对下滑板与坐标面YOX平行的侧面施加Z方向的振动载荷，进行有限元计算。

3 受流系统螺栓联接残余预紧力分析

3.1 残余预紧力与列车运行速度的变化关系

为了研究残余预紧力与列车运行速度的变化关系，笔者给螺栓联接施加相同的初始预紧力，设置不同运行速度的振动载荷。

在4 s内，残余预紧力F与初始预紧力Fn随时间的比值如图5所示。

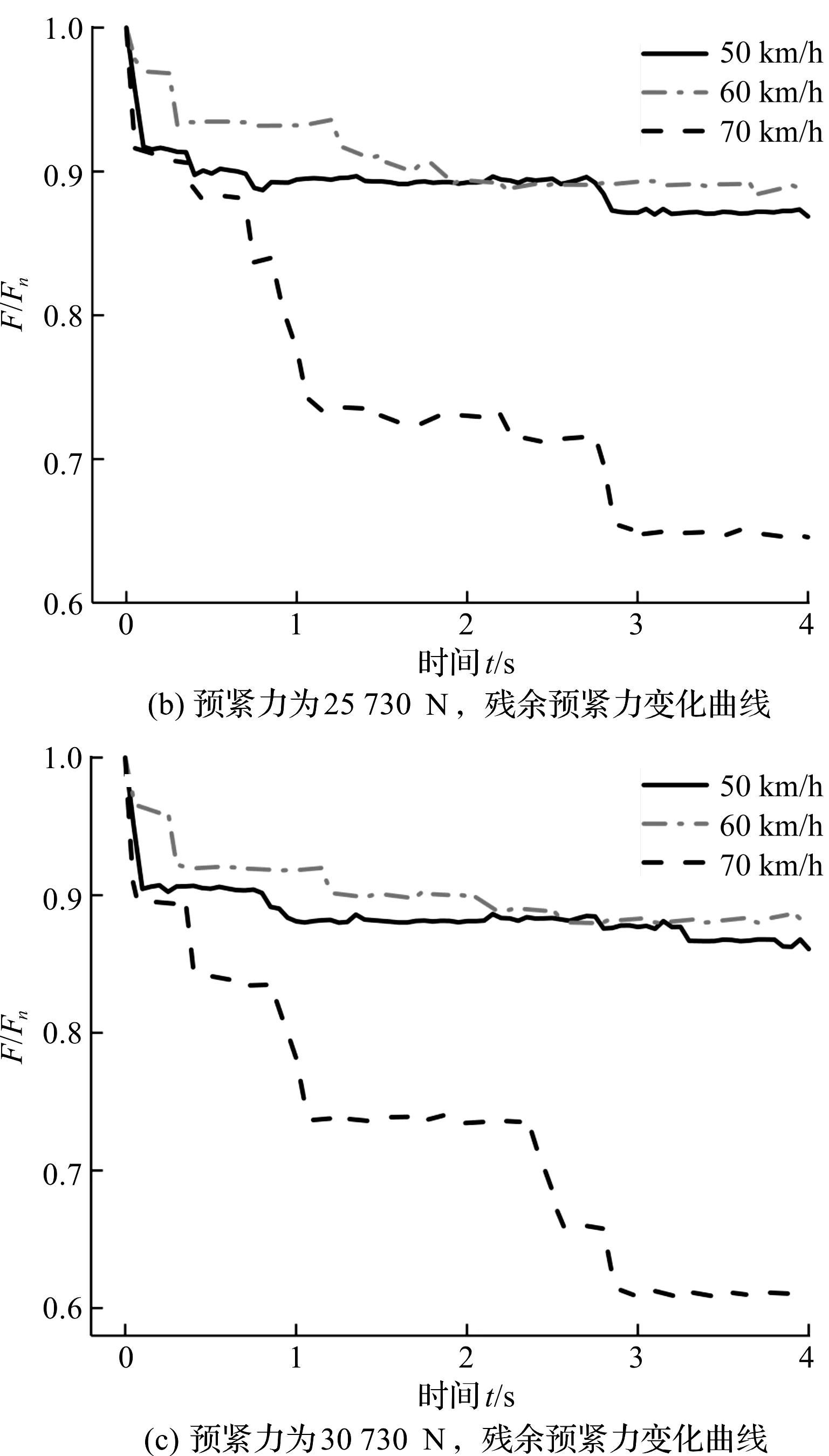
图5 不同运行速度，残余预紧力变化曲线

由图5可知：残余预紧力在运动初期下降的最多。这是因为螺栓联接受到非对称循环位移，由于螺纹升角的存在，螺纹受到非对称循环载荷，螺纹材料产生了棘轮效应，导致塑性变形进一步增大，致使残余预紧力迅速下降。

当列车运行速度为50 km/h和60 km/h时，残余预紧力会趋于稳定，不再变小；而当列车运行速度为70 km/h且预紧力为20 730 N时，残余预紧力持续下降，说明螺栓联接已经失效。这是由于螺栓联接在经过一段时间的非对称循环载荷后，随之载荷所产生的塑性变形已经越来越小，材料塑性应变所产生的变形已经接近弹性变形，最终会棘轮安定。若当棘轮安定时，预紧力产生的接触面间的摩擦力抑制了横向位移导致的相对运动趋势，则螺栓将不会进一步松动，残余预紧力将趋于稳定。反之亦然。所以螺栓联接需要在合适的振动范围内使用。

当列车运行速度为70 km/h，残余预紧力持续下降。所以列车的最佳运行速度区间为50 km/h至60 km/h，否则容易造成螺栓联接防松性能下降，致使滑板脱落，受流稳定性下降。这与1.4所得结果一致。

3.2 残余预紧力与初始预紧力的变化关系

为了研究残余预紧力与初始预紧力的关系，笔者给螺栓联接施加相同的摩擦系数、速度振动载荷，依次设置了17 730 N、20 730 N、25 730 N、30 730 N、350 730 N不同的初始预紧力进行仿真。

残余预紧力F与初始预紧力Fn随时间的比值如图6所示。

图6 不同初始预紧力，残余预紧力变化曲线

由图6可知：初始预紧力过小，并不能起到联接作用。当运行速度处于50 km/h到60 km/h时，初始预紧力为20 730 N，螺栓联接可靠性最佳。随着初始预紧力的增大，残余预紧力与初始预紧力的比值先增大，后减小。这是由于初始预紧力的适当增大，可以有效地提高螺栓联接接触面间的摩擦，从而提高联接的可靠性。但当初始预紧力过大时，材料的棘轮效应明显，加快了材料塑性变形累计速度，从而使残余预紧力下降。

所以，初始预紧力不宜过小或过大，在一定范围内会更加有效地提高螺栓联接的可靠性，以确保受流系统稳定受流。

3.3 残余预紧力与摩擦系数间的关系

为了研究残余预紧力与摩擦系数的关系，笔者给螺栓联接全部接触面设置了0.1、0.15、0.2、0.25的摩擦系数进行比较。

列车运行速度为60 km/h，螺栓联接的初始预紧力为20 730 N，在不同摩擦系数下，残余预紧力F与初始预紧力Fn随时间的比值如图7所示。

图7 不同摩擦系数下残余预紧力变化曲线

从图7可以看出：整体摩擦系数在0.2的时候，螺栓防松性能最佳。

为了进一步研究不同接触面的摩擦系数对螺栓联接松动的影响级别，笔者运用控制变量法，分别对不同螺栓承压面的摩擦系数μ1和滑板接触面的摩擦系数μ2进行数据对比。

对μ1为0.15、μ2为0.1的模型和μ1为0.15、μ2为0.15的模型进行仿真分析，其残余预紧力F与初始预紧力Fn随时间的比值如图8所示。

图8 不同的承压面和滑板接触面摩擦系数下残余预紧力变化曲线

由图8可知：在增加相同的摩擦系数的情况下，增加螺栓承压面更能提高螺栓联接的防松性能。所以优先优化螺栓与滑板的接触面间的摩擦状态，可以提高螺栓联接的可靠性，从而保证受流系统的稳定性。

4 结束语

本文基于受流器使用的实际工况，通过简化模型，在列车运行时，对受流器滑板螺栓联接残余预紧力特性进行了研究，并得出以下结论：

(1)列车运行时的非对称循环振动更容易造成螺栓残余预紧力的下降，残余预紧力在振动初期变化最大。故在第三轨列车行驶行驶前，对受流器螺栓联接防松性能的检测至关重要；

(2)为了保持受流滑板上螺栓连接的可靠性，列车运行速度应不超过60 km/h，最佳运行速度区间为50 km/h至60 km/h时；

(3)螺栓联接的摩擦系数为0.2时，螺栓防松性能最佳；

(4)优先优化螺栓与滑块的接触面间的摩擦状态，有利于提高螺栓联接的可靠性。

参考文献(References):

[1] 郎 鹏.受流器/三轨弯头碰撞动力学研究[D].北京:北京交通大学机械与电子控制工程学院,2016.

[2] 王文娇.受流器与接触轨端部弯头接触特性分析[J].华东交通大学学报,2014,31(1):34-38.

[3] JUNKER H G.New criteria for self-loosening of fasteners under vibration[J].SAE Transactions,1969,78(1):314-335.

[4] NASSAR S A, GANGANALA M. Effect of load eccentricity on the behavior of a bolted joint with a yielded fastener[C].ASME 2009 Pressure Vessels and Piping Conference. American Society of Mechanical Engineers Digital Collection,Vancouver:ASME,2009.

[5] NASSAR S A,MATIN P H.Clamp load loss due to fastener elongation beyond its elastic limit[J].Pressure vessel technology,2006,128(3):379-387.

[6] YANG X, NASSAR S. Vibration-induced loosening performance of preloaded threaded fasteners[C].ASME 2010 Pressure Vessels and Piping Division/K-PVP Conference. American Society of Mechanical Engineers Digital Collection,Bellevue:ASME,2010.

[7] YANG X, NASSAR S A. Effect of thread profile angle and geometry clearance on the loosening performance of a preloaded bolt-nut system under harmonic transverse excitation[C].ASME 2011 Pressure Vessels and Piping Conference. American Society of Mechanical Engineers Digital Collection, Baltimore:ASME,2011.

[8] YANG X, NASSAR S. Analytical and experimental investigation of self-loosening of preloaded cap screw fasteners[J]. Journal of Vibration and Acoustics, 2011,133(3):031007.

[9] 刘建华.轴向激励下螺栓连接结构的松动机理研究[D].成都:西南交通大学摩擦学研究所,2016.

[10] 王传华,王文莉,林清源,等.基于精确建模的横向振动工况下螺栓松动机理研究[J].宇航总体技术,2018,2(4):43-51，64.

[11] 刘传波,孙静明,莫易敏.螺纹紧固件防松性能影响因素研究[J].现代制造工程,2018(4):138-143.

[12] 山本晃.螺纹联接的理论与计算[M].郭可谦，高素娟，王晓凤，等，译.上海：上海科学技术文献出版社,1984.

[13] 黄世钊,吴林杰,向 冰,等.锅炉烟道气吸附塔强度校核与寿命估算化[J].轻工机械,2018,36(3):101-105,111.

[14] 董姝言,杨 扬,齐 涛,等.基于周期对称模型的MW级风电机组变桨轴承连接螺栓强度计算[J].机电工程,2017,34(4):357-360.