基于DEM与MFBD双向耦合的农机触土部件疲劳分析*

张元常，张大斌*，曹 阳,2，刘 洋

(1.贵州大学 机械工程学院，贵州 贵阳 550025；2.贵州大学 工程训练中心，贵州 贵阳 550025；3.中铁五局集团 建筑工程有限责任公司，贵州 贵阳 550025)

0 引 言

农业机械作业时，其触土部件(亦称土壤耕作部件)受土壤颗粒的冲击导致磨损和断裂失效，使其寿命缩短，养护成本增加，直接影响了农业机械的工作效率和可靠性[1-2]。另外，农业机械的工作介质是土壤，作业环境相对比较复杂、特殊，土壤耕作部件发生损坏是磨粒磨损、疲劳磨损和疲劳断裂等多种破坏机制的共同作用结果[3-4]。关于多种破坏机制耦合作用下的农机耕作部件失效机理较为复杂，因此，通过综合性地科学分析农机土壤耕作部件的失效原因，确定导致破坏的各机理的主次作用，对于农机土壤耕作部件结构设计及优化具有重要的指导意义。

磨损和疲劳是土壤耕作部件的两大失效类型[5]。从目前的研究现状来分析，大多数学者主要研究磨损机理导致的破坏，并用于指导触土部件耐磨减阻设计[6-8]。对于磨损失效的评价方法主要有两类：实验室磨损试验和田间试验[9]。然而，对于疲劳失效的研究，由于受现场工作环境和实验测试手段等因素的制约，鲜有学者对触土部件作业中出现的断裂失效问题进行深入研究。随着计算机辅助工程(CAE)的发展，开启了CAE在农业机械寿命预测的应用开端[10]。李鹏涛[11]利用离散元软件EDEM仿真获得了旋耕刀受土壤三向受力和力矩随时间变化的序列值，并导入ADAMS软件，完成了对刀身内部应力谱间接提取和疲劳断裂分析；顿国强等[12]应用EDEM模拟计算得到了深松铲耕作阻力，结合有限元法和恒幅疲劳分析，实现了对深松铲寿命预测和疲劳强度设计。但上述学者对触土部件应力谱的提取相对繁琐，且数据存在等效和简化处理，这种处理方法会给触土部件疲劳仿真结果带来一定的影响。

综合考虑上述问题，本文将以井窖制作机为例,提出一种可适用于触土部件成穴钻头的动应力谱提取方法，研究成穴钻头打穴作业时受土壤激励的动态响应特性，在此基础上对成穴钻头进行疲劳寿命预测。

1 疲劳分析方法

目前，基于动应力的疲劳分析已成为国内外研究的热点之一。吴丹等[13]指出准确预测结构疲劳寿命的关键在于随机激励载荷作用下结构动应力的提取。因此，在疲劳分析过程中，把触土部件所受的动态载荷当做静载荷处理不太理想。本文结合CAE最新发展的技术，提出了基于DEM与MFBD双向耦合提取触土部件动应力谱的方法。

相对于DEM与FEM(有限元法)单向耦合模拟方法，基于DEM与MFBD的双向耦合法可准确模拟几何体与颗粒相互作用的过程，更加真实地反映实际作业情况，准确捕获几何体受力及运动规律变化。目前，市场上存在几款主流的多体动力学软件，如ADAMS、Simpack、LMS Virtual Lab以及RecurDyn等，其中除了Simpack尚不能与EDEM耦合外，其余软件皆可与之实现双向耦合仿真，但仅有递归算法软件RecurDyn能识别与EDEM耦合仿真的柔性体。限于其他仿真软件的局限，本文采用EDEM 2019和RecurDyn V9R2软件联合的方法，来实现DEM与MFBD双向耦合的仿真建模，实现颗粒与柔性结构体的双向耦合仿真，可实时传递和直接地提取数据。

首先，本文利用RecurDyn软件特有的MFBD技术，构建成穴钻头总成装置刚-柔耦合动力学模型；然后，借助离散元软件EDEM选择合适的颗粒接触模型，完成土壤环境的模拟；最后，通过EDEM与RecurDyn耦合，数值模拟成穴钻头-土壤相互作用仿真过程，直接提取成穴钻头的应力载荷-时间历程，结合疲劳分析软件及理论，进行疲劳寿命预测。

触土部件的DEM与MFBD双向耦合疲劳分析流程如图1所示。

图1 DEM-MFBD双向耦合疲劳分析流程

2 成穴钻头总成装置刚-柔耦合建模

2.1 结构组成与工作原理

井窖制作机作为一种新兴的农业机械，具有打穴质量高、劳动强度低和作业效率高等优点，在烤烟栽植过程中发挥着重要的作用。其结构主要由油门操控架、工作头、成穴钻头、软轴、背负式支架和汽油发动机共同组成。其中，成穴钻头是井窖制作机的核心部件，该部件工作时与土壤直接发生接触，是典型的土壤耕作部件。笔者借助SolidWorks三维建模软件进行参数化建模，然后以Parasolid文件格式输出。

井窖制作机装配模型如图2所示。

图2 井窖制作机装配模型1—油门操控架；2—工作头；3—成穴钻头；4—软轴；5—背负式支架；6—汽油发动机

井窖制作机启动后，由汽油发动机输出动力，经软轴传动至工作头，再由工作头转轴带动成穴钻头高速旋转，待成穴钻头转速达到额定转速后，便可操作油门操控架开始向下移动进行打穴作业；在完成烤烟烟垄的井窖穴制作后，返回初始位置，即完成一次完整的作业循环过程。

2.2 多刚体模型的建立

本研究采用RecurDyn多体动力学软件进行建模。为提高仿真效率，笔者对导入的井窖制作机模型进行适当简化，删除汽油机、软轴等部件，对其余部件进行布尔运算，只余下油门操控架、工作头和成穴钻头共同组成的成穴钻头总成装置。

成穴钻头由优质碳素结构钢65Mn热轧板卷(厚度3 mm)制成，其力学性能参数如表1所示。

表1 65Mn力学性能参数

添加成穴钻头总成装置各部件约束关系如表2所示。

表2 成穴钻头总成装置各部件约束关系

2.3 刚-柔耦合模型的建立

复杂土壤条件下工作的成穴钻头总成装置为典型的刚-柔耦合多体系统。考虑到成穴钻头与土壤颗粒间存在大量接触和碰撞的非线性力学行为，故应采用FFlex法，在多刚体模型基础上构建刚-柔耦合多体动力学模型。

笔者利用Simcenter 3D有限元软件对成穴钻头进行清除圆孔和倒角等前处理，并抽取几何中面；结合成穴钻头结构特征，选用2D壳单元CTRIA3划分网格，设定单元边界尺寸为2 mm，生成单元数为28 502个，节点数为14 222个；成穴钻头上端与工作头配合处圆孔设置蜘蛛网状形式的RBE2刚性单元，用于建立运动副和连接工作头；最后以Nastran求解器的SOL 103柔性体解算方案求解，并输出成穴钻头有限元文件dat，将其导入成穴钻头总成装置刚体动力学模型中，用成穴钻头网格形式代替刚体模型，从而建立成穴钻头总成装置刚-柔耦合动力学模型。

3 离散元土壤模型的建立

3.1 颗粒接触模型分析与选型

本研究中烤烟试验地的烟垄为粘性土壤。由于土壤为各项异性材料，物理特性十分复杂，选择合适的颗粒接触模型来生成土壤模型，对提高仿真结果可靠性具有重要的影响。目前，大多数学者[14-15]建立土壤模型的方法主要是采用Hertz-Mindlin(no slip)模型、Hertz-Mindlin粘结模型、Hertz-Mindlin JKR粘结模型、Hysteretic Spring模型以及多接触模型结合方式来建模。然而，在实际作业时成穴钻头与烟垄旋转挤压形成井窖穴的过程中，土壤颗粒间相互作用的过程是呈非线性塑性形变的，上述颗粒接触模型仅能模拟土壤挤压变形过程中产生的线性形变行为。

因此，为准确地模拟成穴钻头与土壤之间相互作用过程，并提取到可靠的工作载荷谱，有必要选择能良好体现土壤应力-应变关系的颗粒接触模型参与仿真。笔者采用具有非线性粘结弹性塑形的接触模型(EEPA)，该模型可有效捕获黏附颗粒的弹塑性变形行为特征，能有效克服上述模型的缺点，比较符合烤烟地烟垄的土壤特性。

3.2 土壤参数标定

仿真分析前，需对烟垄土壤基本力学特性参数和土壤颗粒与成穴钻头间的相互作用参数进行标定；通过对土壤颗粒接触模型选型，在EDEM中建立一个300 mm(长)×300 mm(宽)×300 mm(高)的虚拟土槽；简化土壤颗粒为单球形状，可成倍减少仿真计算量，提高效率，故设定球形颗粒半径为5 mm，共生成31 390个球形颗粒来模拟烤烟地烟垄土质环境。

首先，通过堆积角试验，确定土壤内部相互作用参数。在试验地烟垄取土样，经高周波水分仪DM-100S测得土壤含水率为33%；土壤实际堆积角是采用无底盖有机玻璃圆管(内径90 mm,厚度2 mm,高度225 mm)填满土壤，然后缓慢上移圆管使土壤自然滑落堆积形成；在离散元仿真中土壤内部参数标定以实际堆积角为指标，调整土壤颗粒间相互作用参数，使得生成的仿真堆积角与实际堆积角相同，所得参数即为土壤颗粒间参数的标定结果。

该含水率下土壤的实际堆积角与仿真堆积角对比如图3所示。

图3 土壤实际堆积角与仿真堆积角对比

其次，笔者通过比较仿真与试验中硬度计测头插入烟垄过程的入土阻力来标定土壤与成穴钻头间相互作用参数。

笔者采用型号TYD-3土壤硬度计对烟垄进行入土现场试验。

硬度计入土阻力试验装置如图4所示。

使测头(材质65Mn)以33.33 mm/s匀速插入烟垄土壤；在EDEM仿真软件中构建测头-土壤相互作用仿真模型，通过修正土壤与测头之间参数使仿真值与试验值基本吻合，修正后得到的参数即为土壤-65Mn钢参数的标定结果。

硬度计测头插入土壤的仿真和试验阻力数据曲线如图5所示。

图5 测头插入土壤的仿真与试验入土阻力数据曲线

通过图5可以看出：仿真得到入土阻力曲线呈现出一定幅度的波动，稍加分析原因可知，这是由于在EDEM软件中对土壤颗粒形状、尺寸的适当简化，从而导致仿真值与试验值存在一定的波动和偏差。然而，仿真与试验获得的两曲线总体走势基本一致，表明标定后的仿真参数是可行的，可用于下一步成穴钻头-土壤的耦合仿真。

经过土壤堆积角试验、硬度计测头入土阻力现场试验和仿真标定试验，即完成土壤颗粒基本参数和各项力学参数的标定工作。

最后，汇总烤烟地烟垄的土壤模型仿真参数如表3所示。

表3 土壤模型仿真参数表

4 成穴钻头-土壤耦合建模与分析

基于DEM-MFBD双向耦合的成穴钻头与土壤相互作用的仿真建模是成穴钻头疲劳寿命仿真分析的基础，主要目的是获取成穴钻头在土壤激励作用下的应力分布情况，提供成穴钻头疲劳仿真分析所需的DEM-MFBD耦合仿真后的结果数据，并确定最大应力所处的时刻和位置区域。

实际工程应用中，各类仿真如有限元(FEA)、流体动力学(CFD)、离散元(DEM)和多刚(柔)体动力学(MBD/MFBD)以及它们之间的耦合仿真分析，其开展仿真工作的前提皆是以接近实际作业工况作为其边界条件。因此，为准确模拟成穴钻头总成装置真实运动情况，结合文献[16]知，井窖制作机额定工况下作业效率为2 400穴/h，钻头转速为1 500 r/min，据此设定仿真边界条件。为避免启动瞬间成穴钻头出现冲击载荷影响仿真结果，可使用STEP函数模拟运动，设定成穴钻头运动函数为STEP(time,0,0,3,1 500* 360 d)；油门操控架滑动副运动函数为STEP(time,3,0,4, -300)+STEP(time,4,0,4.5,300)；在RecurDyn环境中，以Wall文件形式输出柔性成穴钻头数据，并导入EDEM，实现两者数据双向实时传递，建立DEM-MFBD双向耦合下的成穴钻头-土壤耦合仿真模型。总仿真时间设为4.5 s，RecurDyn仿真步数为300，EDEM时间步长为自动。进行求解后，可通过RecurDyn后处理模块输出随时间变化的动态应力分布云图信息。

在t=4.035 s时刻，柔性成穴钻头的应力达到最大值36.57 MPa，其应力分布云图如图6所示。

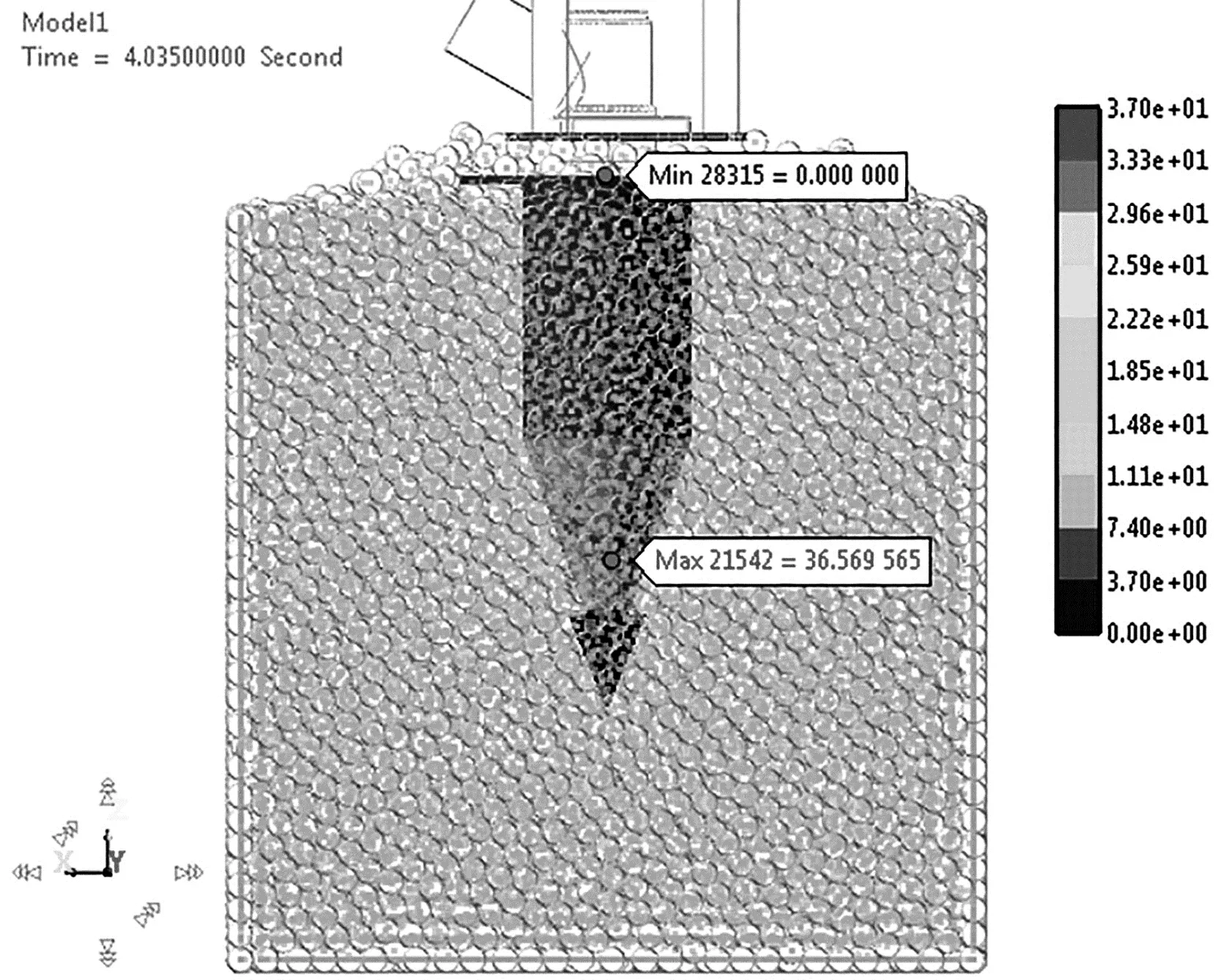
图6 柔性成穴钻头应力分布云图

从图6中可以看出：在该时刻柔性成穴钻头应力值最大，且出现在圆锥面靠小端位置，此时恰逢成穴钻头打入烟垄土壤最深处(200 mm)，该区域应力相对较大，承受土壤颗粒激励的作用力也最大，与实际情况相符。由于柔性成穴钻头模型上最大动应力远小于成穴钻头材料的屈服强度σs=430 MPa，可满足结构件设计的静强度要求。

因此，从柔性成穴钻头受土壤激励的应力动态响应特性结果可以推断，成穴钻头发生的断裂失效现象应属于典型的高周疲劳问题，可基于应力的疲劳分析法，按成穴钻头在一次循环工作过程中承受的载荷谱下展开疲劳寿命研究。

5 成穴钻头疲劳分析

成穴钻头的疲劳寿命研究是在EDEM-RecurDyn耦合仿真结果的基础上，利用疲劳仿真软件协助完成。将修正后成穴钻头的疲劳特性曲线和耦合仿真结果信息输入疲劳仿真软件中，选择合适的载荷谱统计处理方法和疲劳损伤累计理论，可对成穴钻头进行疲劳仿真分析。

5.1 载荷谱提取与统计处理

市场上主流的专业疲劳仿真软件有Nsoft、WinLIFE、FE-safe和FEMFAT等，但能识别和读取RecurDyn中，有限元数据信息的软件仅有一款外部软件FEMFAT和RecurDyn内部疲劳分析模块Durability。考虑到不同软件间数据传递存在失真的情况，故笔者选取与RecurDyn无缝集成的Durability疲劳耐久模块对成穴钻头进行疲劳寿命预测。

提取结构件的载荷谱是进行疲劳仿真分析的前提之一，需要对成穴钻头的载荷情况与载荷的工作周期进行分析。本文基于DEM与MFBD双向耦合仿真分析得到了柔性成穴钻头上各单元节点应力载荷-时间历程的载荷谱。此处需定义成穴钻头的一个工作循环周期，仅截取3 s至4.5 s的仿真数据参与疲劳分析即可。

以最大应力节点21 542为例，其应力载荷-时间历程如图7所示。

图7 最大应力节点21 542的应力载荷-时间历程

由图7可知，成穴钻头各节点承受的载荷谱是复杂随机变化的动应力载荷-时间历程，这是由土壤颗粒对成穴钻头表面的随机激励所致。目前，对随机载荷谱的处理方法主要有两种，即循环计数法和功率谱法。雨流计数法(塔顶法)是工程界应用最为广泛的一种循环计数法，其认为由载荷-时间历程获得的应力-应变迟滞回线与造成的疲劳损伤是等效的，这反应了材料的应力应变行为[17]。

同时，雨流计数法能够如实再现变幅循环加载，被认为是预测疲劳寿命的较好方法，该方法可以识别在复杂随机的载荷序列中与恒幅疲劳数据相似的事件[18]。

因此，笔者采用雨流计数原理，对成穴钻头上各单元节点载荷谱中的应力幅值、平均应力和应力循环作用次数进行雨流循环统计。

以图7的应力载荷-时间历程数据为例，笔者采用Durability模块下的Fatigue Tool/Rainflow Counting功能，得到该节点的载荷雨流统计矩阵，如图8所示。

图8 节点21 542的载荷雨流统计矩阵

5.2 构件S-N曲线计算

由于Durability模块的材料数据库中尚不存在与成穴钻头材料相符合的疲劳特性曲线，在进行疲劳分析前，应先估算出材料的疲劳特性。根据周传月等人[19]的研究结果可知，钢材疲劳与其拉伸特性之间的经验关系已比较成熟。因此，在缺乏65Mn钢疲劳特性试验条件情况下，可根据材料的抗拉强度极限Su来估算。

一般材料的疲劳特性曲线多采用幂函数形式表达，即：

SmN=C

(1)

对上式两端取对数后变形可得：

(2)

式中：N—疲劳断裂时的循环次数；S—对应N的疲劳极限；m,C—与材料有关的常数。

通过查阅机械疲劳手册，笔者选取成穴钻头材料的疲劳极限循环基数Ne=106。该循环基数对应的疲劳极限为：

Sbe=kSu

(3)

式中：Su—材料的强度极限；k—反映不同载荷的作用形式(成穴钻头载荷形式为旋转弯曲载荷，k取0.5)。

在等效循环次数Nreq=103时，等效循环次数对应的等效疲劳极限为：

Sreq=0.9Su

(4)

由式(3，4)计算得到的双对数坐标系(lgS-lgN)下材料疲劳特性曲线中，A、B两点坐标分别为(3，2.820 5)和(6，2.565 3)。进一步计算得材料高周疲劳区间(N=103～106)的lAB线段方程为：

lgS=3.075 8-0.085 1lgN

(5)

通过材料疲劳特性曲线来计算机械结构件的疲劳寿命往往趋于理想化，而且实际工程中的机械结构件存在应力集中、形状尺寸和表面加工工艺等因素，对结构件疲劳强度有较大的影响；同时，对于由同种材料制造出来的不同结构件，其疲劳特性曲线也往往存在较大差异。因此，在实际工程应用中，在对结构件进行抗疲劳强度设计和疲劳寿命预测时，必须考虑主要的疲劳影响因素，把材料疲劳特性曲线修正转化为相应结构件的疲劳特性曲线，才可获得较为准确的疲劳分析结果。

本文采用赵少汴[20]提出的修正方法，在循环次数N≤103时，上述疲劳影响因素对材料不产生影响；当循环次数N≥106时，材料疲劳强度将降低Kσ倍，Kσ(疲劳强度降低系数)的计算公式为：

(6)

式中：Kt—理论应力集中系数；β—表面质量系数；ε—结构件的尺寸系数。

通过查找《抗疲劳设计─方法与数据》[21]，笔者得到65Mn在该情况下Kt的取值为2；结合构件表面粗糙度，查得β值为0.85；ε值可通过经验公式[22]计算得到，即：

(7)

式中：v—成穴钻头的体积；v0—标准试件的材料体积。

将相关数据代入式(7)中，可求得该结构件尺寸系数ε为0.9。

当循环次数N=106时，疲劳极限修正公式为：

(8)

经上述修正方法，将标准试件材料S-N曲线进行修正，可得到实际结构件S-N曲线。通过计算可得到成穴钻头疲劳特性曲线的高周疲劳区间lAB＇线段斜率k1为：

(9)

结合式(6，8，9)，并代入数值，经计算可得到k1=-0.212 9，反斜率k=-1/k1=4.697 0。经过进一步推导，可得成穴钻头疲劳特性曲线高周疲劳区间的lAB＇线段方程为：

lgS=3.459 2-0.212 9lgN

(10)

一般认为应力幅低于疲劳极限时，结构件不会产生破坏，故疲劳特性曲线达到疲劳极限后变成一条水平直线，表示构件具有永久寿命。然而有关文献[23-25]指出：低于疲劳极限的应力循环仍然对构件产生疲劳损伤。因此，笔者采用海巴赫法则(modified miner rule，MM)，对疲劳极限下的小载荷进行修正。以lgS-lgN曲线转折点B＇(6，2.181 7)为起点，lB＇C＇线段斜率k2=-1/(2k-1)，算得k2=-0.119 1，可推出lB＇C＇线段方程为：

lgS=2.896 3-0.119 1lgN

(11)

材料65Mn和修正后成穴钻头的S-N曲线如图9所示。

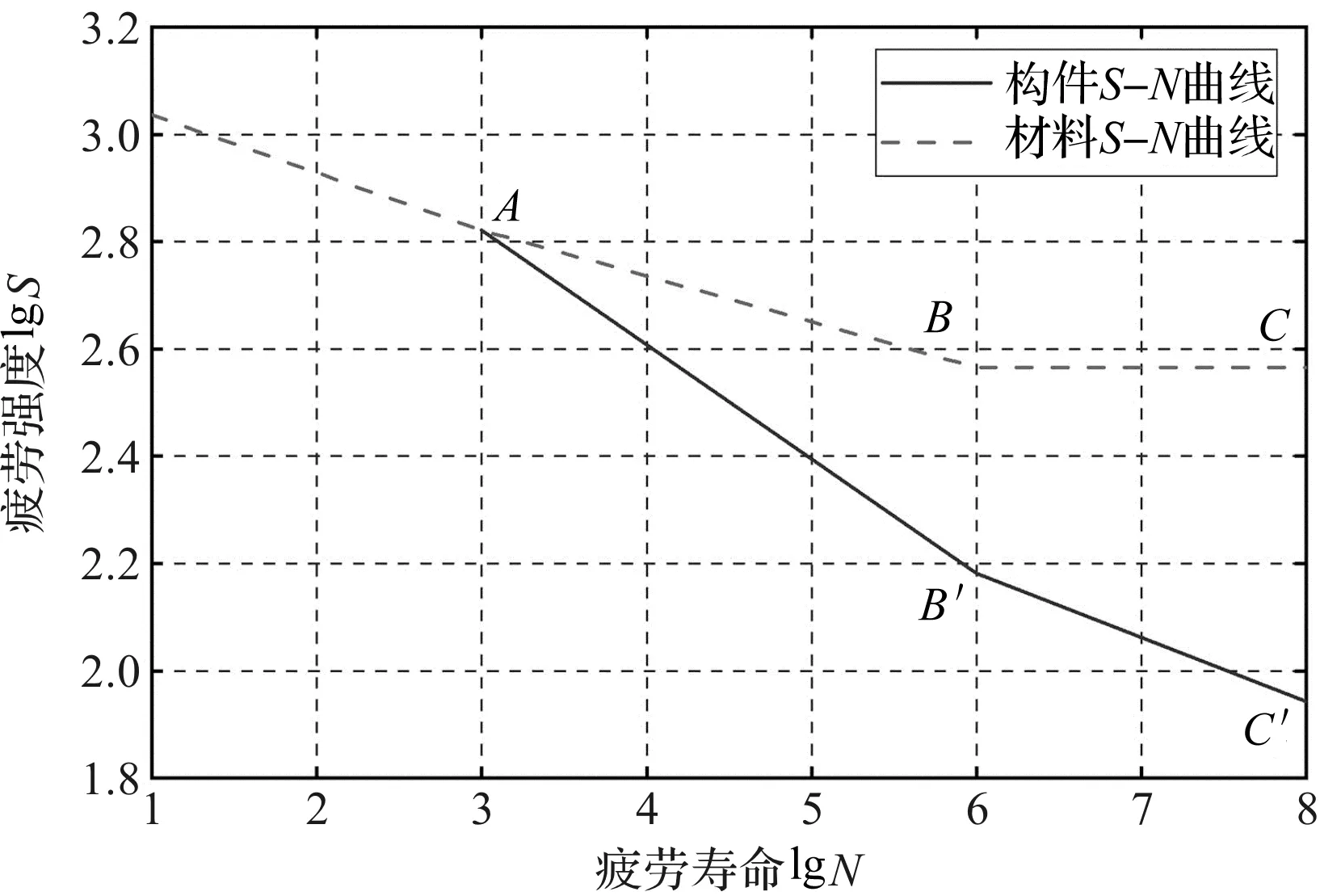
图9 材料65Mn与修正后成穴钻头的S-N曲线

5.3 疲劳寿命计算

基于应力谱预测疲劳寿命，本文在Durability模块中输入修正后的构件S-N曲线；考虑平均应力的影响，笔者对雨流计数法处理过的载荷数据，选择较为保守的Goodman公式，对构件各节点应力循环均值不为0的载荷谱进行修正；应用Palmgren-Miner线性疲劳损伤累计理论，可得如图8所示载荷雨流统计矩阵中第i行、第j列载荷块对构件所造成的损伤度为：

(12)

式中：nij—构件在第i级应力幅值和第j级应力均值载荷作用下的循环作用次数；Nij—构件在第i级应力幅值和第j级应力均值载荷作用下发生破坏时的疲劳寿命。

进而可得到与雨流统计矩阵所对应的总损伤度为：

(13)

当总损伤D=1时，则表明构件发生疲劳破坏。因此，可经Durability/Fatigue Evaluation功能块，计算得到成穴钻头在该载荷谱下的最大疲劳损伤值约为4.067E-06。

根据疲劳寿命L=1/D，可获得成穴钻头的最小疲劳寿命为245 902次，并输出成穴钻头疲劳寿命分布云图，如图10所示。

图10 成穴钻头疲劳寿命分布云图

由图10可知：圆锥面区域为成穴钻头的疲劳寿命薄弱区域，越靠近圆锥面小端处寿命越小，表明成穴钻头作业时，圆锥面受土壤的激励作用较大；且此处结构相对较薄(厚度3 mm)，抗疲劳能力较差，容易发生疲劳断裂。

根据仿真得到该载荷谱作用下最小环循次数为245 902次，按照挖穴速率2 400穴/h来计算，可得成穴钻头最小疲劳寿命约为102.46 h，且预测的破坏位置与文献[26]中图1展示的实际发生断裂位置基本一致，与烟农反馈的使用情况基本吻合，验证了基于DEM与MFBD双向耦合疲劳分析方法的合理性和可行性。

6 结束语

本文提出了一种基于DEM与MFBD双向耦合的疲劳分析方法，完成了对触土部件成穴钻头的寿命预测，主要研究过程及结论如下：

(1)实测烤烟地烟垄土壤颗粒参数，分析标定土壤与成穴钻头之间的力学特性参数，应用RecurDyn的MFBD技术和EDEM的EEPA接触模型，构建适应于烤烟地土质环境下的成穴钻头-土壤相互作用仿真模型，获得了成穴钻头工作时的应力动态响应特性；

(2)基于DEM与MFBD双向耦合法可直接提取成穴钻头的应力载荷-时间历程，克服了无法通过试验测试触土部件破坏位置处应力应变载荷的问题；

(3)利用修正后成穴钻头的S-N曲线，结合Palmgren-Miner法则，通过RecurDyn/Durability模块预测得到成穴钻头最小疲劳寿命约为102.46 h，并确定了薄弱区域主要位于圆锥面靠小端，这与成穴钻头在实际服役状态下结构的疲劳寿命和断裂失效位置基本吻合，验证了基于DEM与MFBD耦合疲劳分析方法的合理性；

(4)成穴钻头为典型的农机触土部件，故DEM与MFBD双向耦合预测疲劳寿命的方法具有一定的通用性，在仿真模型和参数准确的前提下，可为旋耕刀、深松铲等触土部件的疲劳强度分析提供有价值的参考。

参考文献(References):

[1] 贾洪雷,王万鹏,陈 志,等.农业机械触土部件优化研究现状与展望[J].农业机械学报,2017,48(7):1-13.

[2] 李庆达,郭建永,胡 军,等.土壤耕作部件耐磨减阻处理的研究现状[J].表面技术,2017,46(2):119-126.

[3] 王会强,蒋 辉,邢艳秋,等.农业机械常见的失效分析[J].农机化研究,2008(9):28-30.

[4] 苏彬彬,徐 杨,简建明.农业机械耐磨件发展及研究现状[J].热处理技术与装备,2013,34(5):53-58.

[5] 王小飞.超声波辅助等通道转角挤压处理农业机械触土部件用材摩擦学性能研究[D].郑州：河南农业大学机电工程系,2018.

[6] 张 帅.几种工程机械工作部件触土曲面的微分几何性质及其减阻力学特性研究[D].洛阳：河南科技大学车辆与交通工程学院,2014.

[7] 罗晓峰.大豆耕播机触土关键部件设计及测试技术研究[D].长春：吉林大学生物与农业工程学院,2017.

[8] 贾洪雷,罗晓峰,王文君,等.耕作部件耦合仿生表面结构制备方法[J].农业机械学报,2016,47(S1):130-135.

[9] 吴志立,赵建杰,吴明亮,等.农机土壤工作部件耐磨强化研究进展[J].中国农机化学报,2016,37(8):256-264.

[10] 向卫兵.机械寿命的CAE分析及其在农业机械中的应用[J].农机化研究,2012,34(12):48-51.

[11] 李朋涛.旱作土壤中旋耕刀失效速率模型及选型优化研究[D].北京：中国农业大学工学院,2018.

[12] 顿国强,陈海涛,纪文义.基于EDEM仿真与SolidWorks Simulation的凿式深松铲有限元分析[J].河南农业大学学报,2017,51(5):678-682.

[13] 吴 丹,郭富强,马 琳.基于多体动力学的车轴动应力分析及寿命研究[J].机械设计,2019,36(2):52-56.

[14] 马跃进,王 安,赵建国,等.基于离散元法的凸圆刃式深松铲减阻效果仿真分析与试验[J].农业工程学报,2019,35(3):16-23.

[15] 石林榕,赵武云,孙 伟.基于离散元的西北旱区农田土壤颗粒接触模型和参数标定[J].农业工程学报,2017,33(21):181-187.

[16] 戚源明,张富贵.现代山地烟叶生产机械化技术[M].北京：中国农业出版社，2018.

[17] 尚德广.疲劳强度理论[M].北京:科学出版社，2017.

[18] 李永利.疲劳试验测试分析理论与实践[M].北京:国防工业出版社，2011.

[19] 周传月,郑红霞,罗慧强,等.MSC.Fatigue疲劳分析与应用实例[M].北京:科学出版社,2005.

[20] 赵少汴.有限寿命疲劳设计法的基础曲线[J].机械设计,1999(11):5-7，11.

[21] 赵少汴,王忠保.抗疲劳设计─方法与数据[M].北京:机械工业出版社,1997.

[22] 黄 宁,黄明辉,湛利华.新的缺口试样尺寸系数经验公式[J].华南理工大学学报：自然科学版,2012,40(12):35-40.

[23] 郑松林,黄崇文,冯金芝,等.基于高耐久寿命的减速器壳体轻量化实现方法[J].机械强度,2018,40(1):95-99.

[24] 彭晨晨,秦宝荣,贾夫洋,等.基于刚柔耦合的搁脚机构动态仿真及疲劳寿命分析[J].机电工程,2018,35(7):685-689.

[25] HAIBACH E. Modified linear damage accumulation hypothesis accounting for a decreasing fatigue strength during increasing fatigue damage[R]. Darmstadt：LBF, 1970.

[26] 胡长寿,喻丽华,徐志波,等.烟苗移栽井窖制作机关键部件改进及试验[J].农机化研究,2019,41(10):198-202.