某连续钢箱曲梁在竖向荷载作用下的试验研究

李卓庭,宋郁民

(上海工程技术大学 城市轨道交通学院,上海,201620)

曲线梁作为现代交通工程中的一种重要结构形式,因其占地面积小、支撑条件灵活、造型美观协调及保证线形平顺等优点,被广泛应用于城市交通主干线、立交桥以及山区公路。相比于直线梁桥,曲线梁桥力学性质、构造、荷载及施工等方面都更为复杂。其中最为重要的是其结构受力不仅承受弯矩和剪力,还有较大的翘曲和扭转作用,弯扭耦合的影响也较大[1]。为了保证其运营的安全性和舒适性,需要对曲梁在荷载作用下的变形进行研究,通过试验测得竖向、横向位移、分析曲梁扭转变形情况[2]。目前国内外曲梁荷载试验比较少见,此次研究以两跨连续曲梁为研究对象,结合相关规范中的指标要求,通过施加与设计荷载等效的试验荷载,进行相关的检测、记录、分析及评定工作,主要有试验筹备、实验进行、理论模型分析、理论和实测结果对比等几个环节[3]。通过对两跨连续曲梁进行荷载试验,对比分析荷载试验获得的测试结果和有限元计算值之间的关系,综合评价曲梁在使用状态下的变形情况。

1 工程概况

单轨半径100 m两跨连续钢箱曲梁,梁体为钢结构变截面,结构形式为两跨连续梁。曲梁半径100 m,全长23.073 m,跨径为(10.68+10.99)m;跨中梁高1.24 m,支点梁高1.49 m;梁宽0.69 m,主要材质为Q460qENH,行驶速度为32 km/h。曲梁平面、立面图如图1、2所示。

图1 曲梁平面图

图2 曲梁立面图

2 静载试验

2.1 实验内容

此次荷载试验主要有以下几个测试内容：第一,采用软件Midas.civil计算1.0倍设计荷载下的内力值和变形,使用结构力学求解器绘制出各测试截面的影响线,得出最不利加载。按照各个测试截面的影响线和最不利加载,计算各个测试截面的最大内力R,进行分级加载,测试轨道梁控制截面的竖向和横向挠度,评价曲梁在正常使用状态下刚度等是否满足规范要求;第二,逐级增大试验荷载加载值,每级增量为最大内力值R的10%,研究结构的安全储备。

本次试验共进行了两次循环加载,加载到规定荷载后,再进行下一级加载,逐级加载到K=超加载1.5,测试其挠度。分以下3个加载组合进行分析讨论：1.0倍列车荷载+二期恒载、1.3倍列车荷载+0.3(结构自重+二期恒载)和1.5倍列车荷载 +0.5(结构自重加二期恒载)。

2.2 测点布置及采集设备

根据连续梁受力特点,选取跨中最大正弯矩截面、支座最大负弯矩截面、固定端截面最大剪力处为测试截面,如图3所示的A、B、C 3个截面为弯矩测试截面,D、E为最不利剪力测试截面。共计5个截面。

此次静载试验测试应变采用如图4所示的东华DH3818N静态应变测试系统,挠度采用如图5所示的YHD-50电测位移计进行测量(该仪器精度为±5 με)。

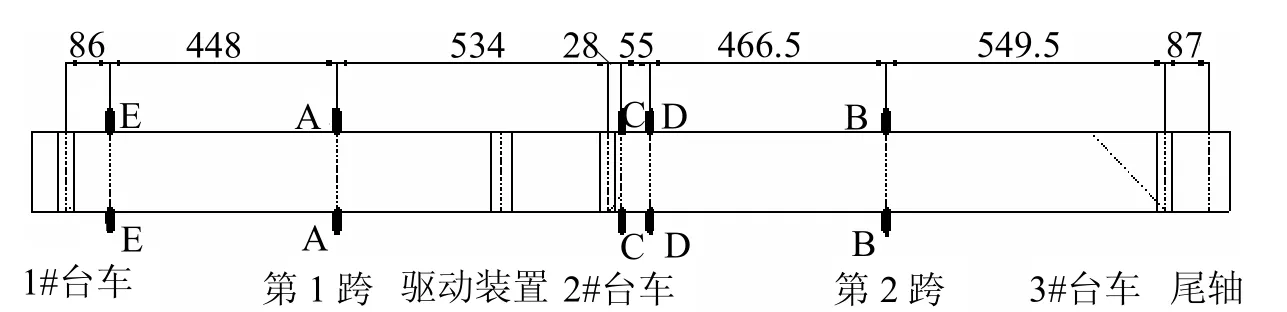
图3 曲梁测试截面(单位：cm)

图5 电测位移计

2.2.1 刚度测试截面测点布置

挠度测试选取A、B两个跨中截面,在每个测试截面的曲梁凸侧上下各布置4个电测位移计,距边缘各5 cm左右,共布设8个位移计。每个测试截面测点布置如图6所示。

2.3 试验荷载工况

静载试验是通过试验荷载加载检验结构截面应力状态及整体变形情况,其试验荷载及加载工况的确定尤为重要。根据有限元分析计算结果和规范要求,选取典型截面进行试验,试验中,列车活载按6辆编组的AW2型列车进行等效加载,试验轴重取P0=140 kN,AW2轴重P=120 kN,活载图式如图7所示。

本次静载试验荷载采用反力架加载。反力架加载以模拟列车轴重荷载为原则,试验采用4个门式反力架。依据“测试截面的试验加载最大内力值与设计荷载下内力值近似相等”原则,确定每个反力架的加载位置,如图8,工况设计结果如表1所示。

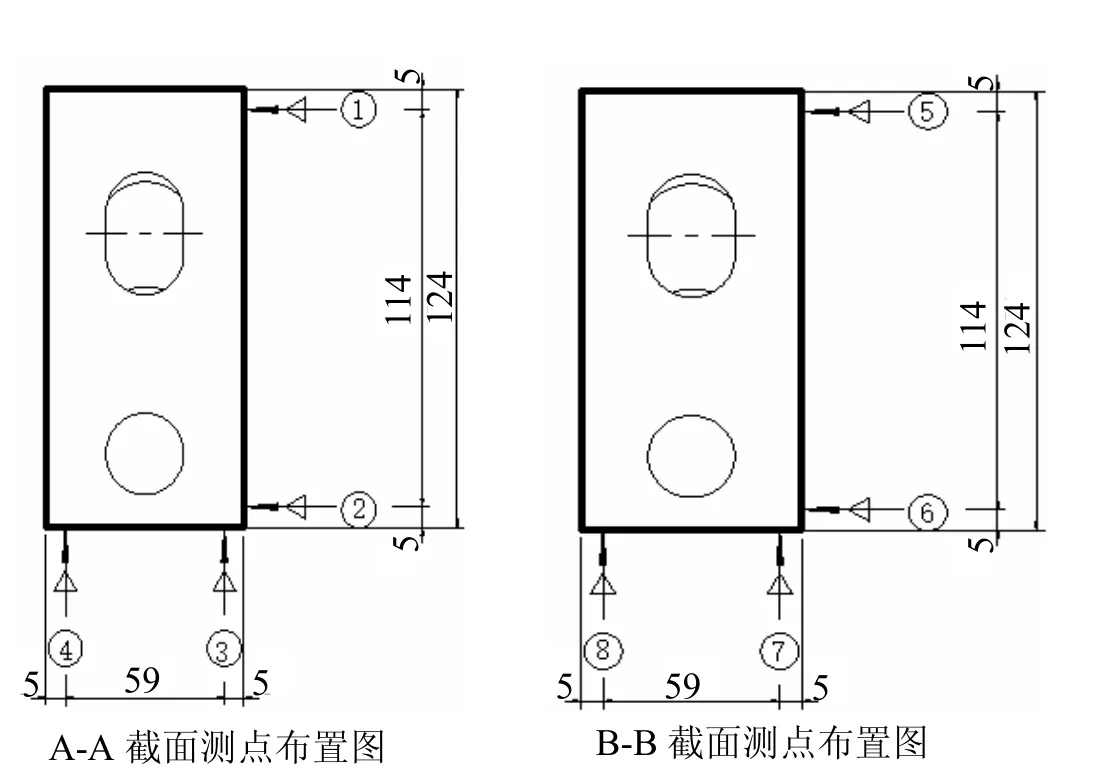
图6 位移测点布置图(单位：cm)

图8 反力架加载示意图

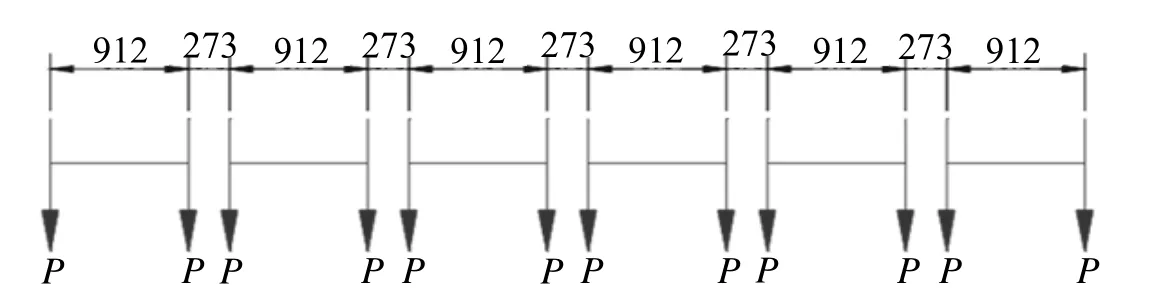
图7 列车活载图式(单位：cm)

表1 荷载工况

为确保试验加载效率,在每个千斤顶与反力架之间布置压力传感器校核千斤顶加载误差。现场加载实景如图9所示。

图9 试验现场反力架、千斤顶及压力传感器

3 有限元模型分析

3.1 曲梁建模

利用桥梁有限元软件Midas civil建立分析模型,曲梁通过梁单元进行模拟,用梁格法进行建模。定义钢材的型号为Q460qENH,分别选取跨中和支点的截面尺寸定义截面1、2,选取第1跨支点至跨中、跨中至支点两个截面尺寸定义两个变截面3、4,第2跨采用同样的方式定义变截面5、6。曲梁结构模型如图10所示[4]。

按照相关桥梁设计规范规定,通过移动活载影响线分析,提取试验方案关键截面的最不利内力对应的活载布置情况,通过有限元模拟工况1～5的荷载形式,如图11所示。

图10 曲梁有限元模型图

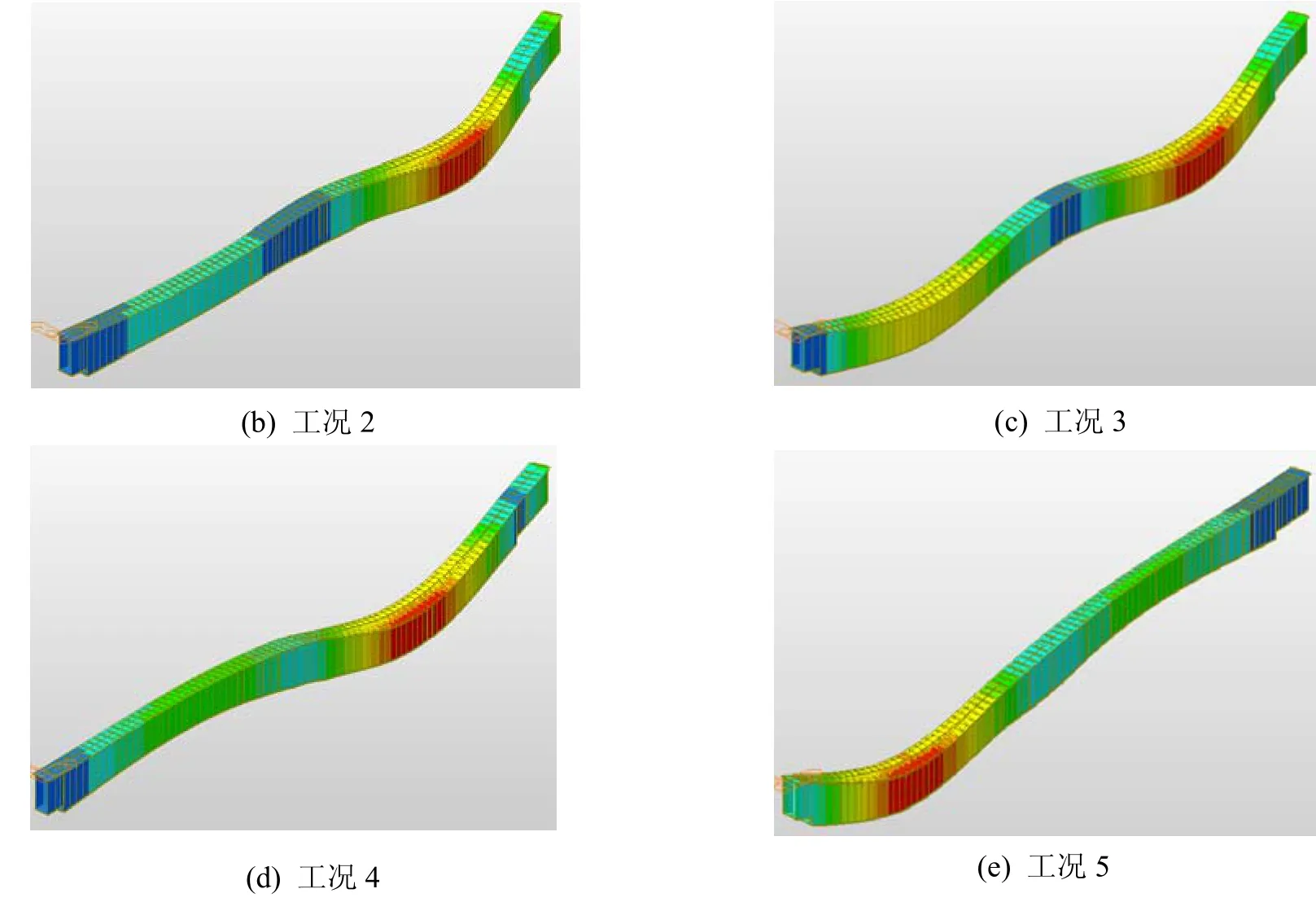
图11 曲梁有限元模型加载图

提取不同工况下结构变形与实测结果进行对比。从表2、3可知,竖向挠度校验系数最大为0.84,横向挠度校验系数最大为0.78,曲梁实测挠度值均小于迈达斯理论计算挠度值,表明结构刚度有一定的变形储备。

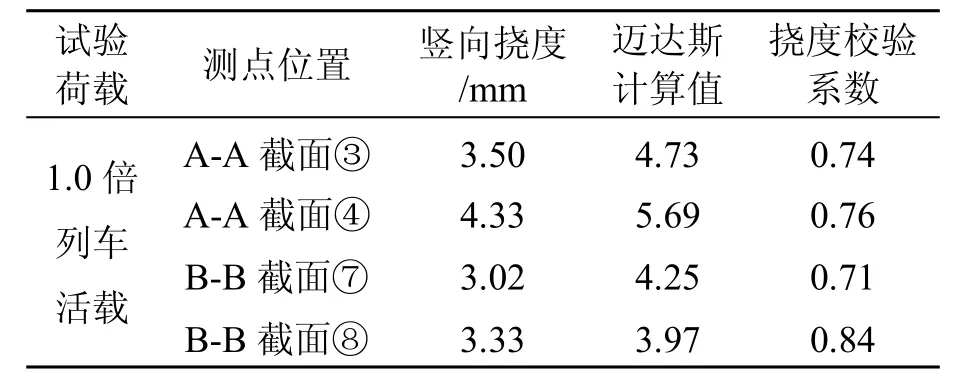
表2 竖向挠度实测值与理论挠度值

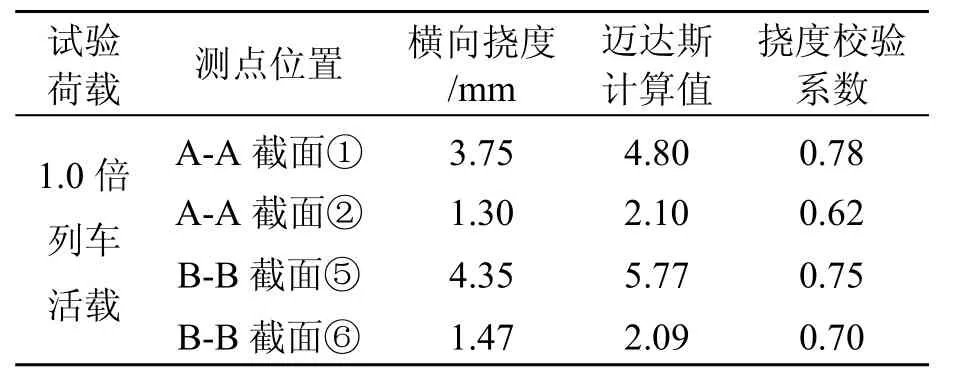
表3 横向挠度实测值与理论挠度值

4 试验结果分析

4.1 竖向挠度测试结果分析

两跨连续曲梁跨中截面在加载状态一试验荷载作用下,各跨中挠度实测值,如表4所示。

依据设计要求的刚度限值[5-9],实测静活载挠跨比小于L/900,挠度值不得大于限值：f实测≤L/900=10 680/900=11.9 mm,则在1.0倍设计活载作用下：第1跨跨中A-A截面实测挠跨比：f实测/L=3.5/10 680=1/3 051＜1/900,第2跨跨中B-B截面实测挠跨比：f实测/L=4.33/10 680=1/2 467＜1/900,故梁体的竖向刚度满足要求。

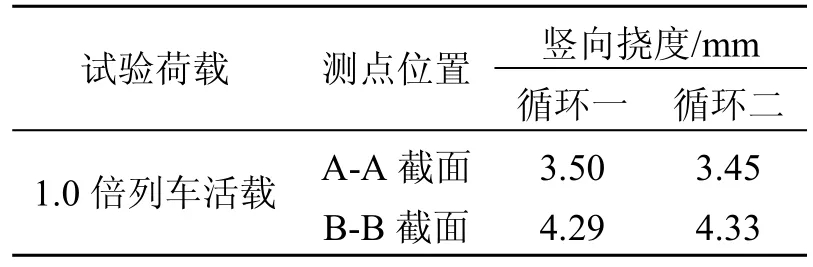
表4 1.0倍列车计活载作用下跨中截面最大挠度值/mm

依据实测挠度,进行结构变形分析。选取K=“二恒(1.0)”～K=“超加载(1.5)”中各级加载值与循环2实测的第1跨跨中A-A截面位移挠度值和第2跨跨中B-B截面位移挠度值进行线性拟合,得拟合曲线如图12、13所示。

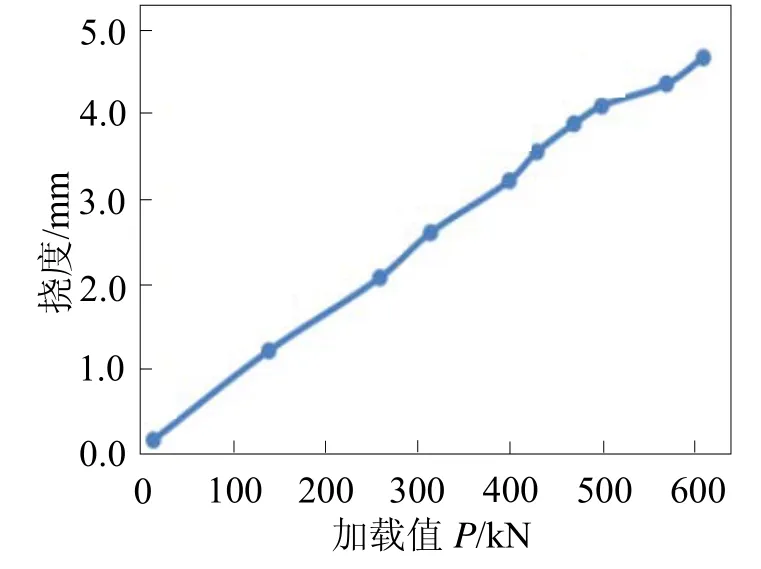
图12 第1跨跨中A-A截面加载荷载值—竖向挠度值拟合曲线

图13 第2跨跨中B-B截面加载荷载值—竖向挠度值拟合曲线

由图12、13可知,荷载与挠度呈线性关系,且第1跨跨中A-A截面拟合的线性相关系数为0.999,第2跨跨中B-B截面拟合的线性相关系数为0.995,故两跨连续曲梁在K=1.5设计超加载作用下,结构处于线弹性工作状态。

对两次循环的相对残余变形进行分析(如表5所示)。由表5可知,试验荷载作用下,跨中截面相对残余变位为0.394%～3.684%,均小于20%。参照《公路桥梁承载能力检测评定规程》,梁体相对残余变位(残余变形增量/总变形增量)满足要求。

表5 试验荷载作用下跨中截面实测残余变形

4.2 横向挠度测试结果分析

曲梁跨中截面在各工况试验荷载作用下挠度实测值,如表6所示。由表6可知,第1跨跨中A-A截面测点最大横向挠度为3.75 mm在工况4测得。第2跨跨中B-B截面测点最大横向挠度同样在工况4中产生,值为4.35 mm。

选取K=“二恒(1.0)”～K=“超加载(1.5)”中各级加载值与工况4实测的第1跨跨中A-A截面位移挠度值和第2跨跨中B-B截面位移挠度值进行线性拟合,得拟合曲线如图14、15所示。

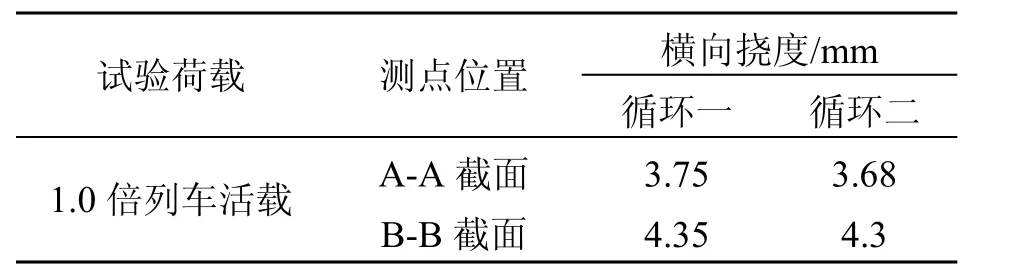
表6 1.0倍列车计活载作用下跨中截面最大挠度值/mm

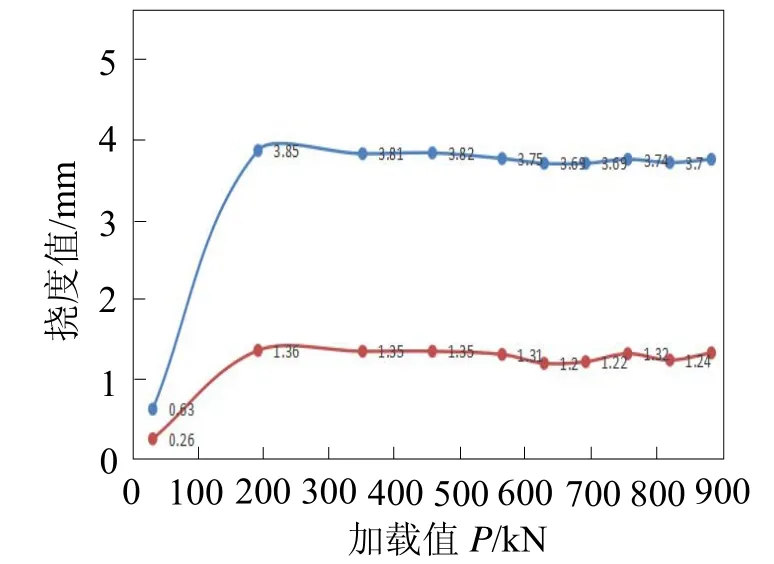
图14 第1跨跨中A-A截面加载荷载值—横向挠度值拟合曲线

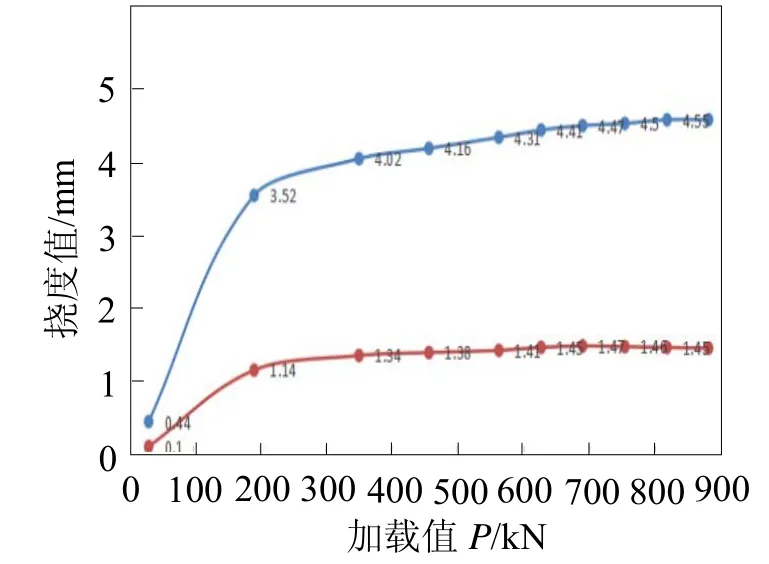
图15 第2跨跨中B-B截面加载荷载值—横向挠度值拟合曲线

由图14、15中曲线分布规律可知,在荷载小于200 kN时,曲线基本呈直线状,而且荷载与挠度成正相关,此时结构处于线弹性工作状态。当荷载超过200 kN时,曲线基本保持不变且略微有上下浮动趋势。这是由于结构在承受竖向荷载作用时,结构不仅发生弯曲,同时因受曲率的影响而产生扭转,产生“弯扭耦合”现象。一开始曲梁在加载力的作用下发生竖向位移和横向位移,当横向位移增大到某一程度时,可能出现加载力的作用点发生偏离的情况,偏离梁顶中性轴,使得曲梁发生偏心加载,且曲梁为钢箱曲梁,曲梁设有的内横、竖隔板导致曲梁内部产生应力集中现象,加载力在梁内发生不均匀分布,导致加载后期只发生竖向位移,而横向位移基本保持不变。如果不考虑发生偏心加载情况,结构未发生偏心加载,随着荷载的增加结构扭转变形程度的增大,梁端约束使得曲梁产生的纵向正应力增大,从而产生向曲面内侧的横向抗力增大,当荷载加载超过200 kN后,曲面内侧的横向抗力与竖向加载时产生的横向分力达到平衡,导致横向位移基本处于稳定不变状态,且结构仍处于线弹性状态。

由试验所得数据计算出控制截面挠度平均值和相对残余挠度值(见表7),挠度值以曲梁圆心向外为正,反之为负。由表7可知,相对残余挠度变位最大为17%(满足规范小于20%的要求),说明加载至1.5倍列车荷载后结构大致恢复原状,加载后期处于非弹性工作状态。

表7 试验荷载作用下跨中截面实测残余挠度

4.3 翘曲、扭转变形分析

由于荷载实验所测得的横向位移在工况4加载情况下最大,选择在工况4条件下测得的第1跨跨中A-A截面和第2跨跨中B-B截面的位移测点,计算出控制截面的扭转角。假设曲梁跨中截面外侧在竖向荷载作用下发生的变形如图16所示。

由公式θ=l/r计算可得：第1跨跨中A-A截面测点①处的扭转角θ=(3.75/119× 180°=5°40′; 第 1跨跨中 A-A 截面测点②处的扭转角θ=(1.3/5)×180°=46°48′;第2跨跨中B-B截面测点处⑤的扭转角θ=(4.35/119)×180°=6°35′;第2跨跨中B-B截面测点处⑥的扭转角θ=(1.47/5)×180°=52°54′。由计算结果可以看出,①、⑤处的扭转角明显小于②、⑥处的扭转角,由此可知当施加竖向荷载时,曲梁外壁未维持平面状态,发生向外的凸向变形。

由表7可知,在两跨跨中A、B截面的横向测点位移中,距梁顶较近测点①、⑤的位移大于距梁顶较远测点②、⑥的位移,说明曲梁有半径向外方向的扭转趋势。在测试的竖向位移测点中,距曲梁半径方向较近测点③、⑦的位移大于较远测点④、⑧的位移,由此可知,由于曲梁发轻微扭转,使得曲梁受到竖向荷载加压后,力没有均匀从梁顶传向梁底,梁顶靠半径向外测点位置的力小于靠里的力,曲梁底面不均匀受力,导致同一截面的竖向位移存在差异,发生翘曲。

图16 跨中截面竖向位移测点扭转分析图

5 结论

此次试验以某连续钢箱曲梁为测试研究对象,根据有限元计算分析和现场静力荷载试验,得到以下结论：(1)将理论计算值和实验值比较分析,竖向挠度校验系数最大为0.84,横向挠度校验系数最大为0.78,曲梁实测挠度均小于理论计算挠度,表明结构刚度有一定的变形储备;(2)列车静活载作用下,曲梁跨中截面实测竖向挠度最大值4.33 mm,满足梁体竖向刚度的要求。荷载与竖向挠度呈线性关系,且其相对残余变位小于20%,结构处于线弹性工作状态。曲梁跨中最大挠跨比为1/2467在工况4下的第2跨中截面取得,满足《跨座式单轨交通设计规范》的刚度限值小于1/900的要求;(3)列车静活载作用下,第1跨中截面测点最大横向挠度为3.75 mm。第2跨中截面测点最大横向挠度值为4.35 mm。在荷载小于200 kN时,荷载—横向挠度曲线基本呈直线状,荷载与挠度成正相关,结构处于线弹性工作状态。当荷载超过200 kN时,曲线基本保持不变且略微有上下浮动趋势,且横向相对残余挠度最大为17%,满足规范小于20%的要求,说明结构加载至1.5倍列车荷载后整体大致恢复原状,加载后期处于弹性工作状态;(4)曲梁侧面同一截面的上缘和下缘两测点,计算出的扭转角相差较大,且上缘小于下缘,说明曲梁在竖向荷载下,曲梁外壁未维持平面状态,发生了向外的凸像变形;(5)在两跨跨中A、B截面的横向测点位移中,距梁顶较近测点位移大于距梁顶较远测点位移,说明曲梁有半径向外方向的扭转趋势。在测试的竖向位移测点中,距曲梁半径方向较近测点位移大于较远测点位移,说明曲梁同时发生翘曲变形。