考虑路侧停车需求的城市办公区单行交通组织优化

曹文娟, 贾顺平, 邵 文

(北京交通大学交通运输学院，城市交通复杂系统理论与技术教育部重点实验室，北京 100044)

随着中国城市化进程的加快，交通拥堵成了许多大中城市面临的突出问题。在很多城市，交通拥堵一般体现在主干道上，很多次干路、支路却利用率低下，有限的城市道路资源没有得到充分利用[1]。单行交通是一种有效的道路交通管理措施，通过科学合理的组织及实施，能均衡道路网内部交通压力的时空分布，提高道路瓶颈路段的服务水平[2]。

中外学者已经较为深入地研究了单行交通组织实施及其效果评价。Davies[3]对单行交通组织优缺点及实施后的影响(包括经济效益)进行了分析，但仅对单行交通的优缺点进行定性分析，缺少量化分析；邬郁儒[4]则在定性分析的基础上选取评价指标，利用层次分析法和线性模糊分布法计算，进行效果评价；奇格奇等[5]利用交通仿真量化方案实施前后车流密度、排队长度等指标，进而为方案评估与决策提供数据支持；Drezner等[6]以路网内用户出行时间最短为目标，对路网中单行交通设置方案进行了研究。随着城市交通的发展，对单行交通设置与评价方法要求越来越高，较多学者进行单行交通组织优化建模，设计启发式算法加以求解。龙东方等[7]以路段饱和度最大和车辆绕行距离最短为目标建立双层规划模型，并设计模拟退火算法求解；王英姿[8]从路段饱和度超限量及车均绕行系数两方面入手，在此基础上进一步考虑了支路双向车流的相互影响因素，建立双层规划模型，运用模拟退火算法求解，对比等量划分支路双向通行能力的优化方法，求解结果明显更优；陈群等[9]除考虑支路通行能力之外，还分析了驾驶员的路径选择行为，对城市微循环交通组织进行优化。

在单行交通方案优化方面，既有研究以城市整体道路网为优化对象，模型构建主要从提高交通效率角度出发，通常以路网的行程时间、路段饱和度等指标作为目标，少有研究考虑停车需求因素在单行交通组织优化时的重要性。在城市化快速发展的背景下，停车设施供应无法满足日益增长的停车需求，特别是在城市中心区路网[10-11]。对于日间路侧停车需求较大的城市办公区路网，除了交通效率，尚需进一步考虑路侧停车因素。在既有研究基础上，综合考虑路段平均饱和度最小化、车辆绕行系数最小化及最大化满足路侧停车需求三方面，建立多目标的单行交通组织双层规划模型，采用嵌套Frank-Wolf算法的遗传算法求解，最后通过案例分析证明本文提出模型与算法的可行性。

1 问题描述

研究对象为城市办公区内部道路单行交通组织方案。办公区通常由主(次)干道作为其周边道路，内部区域由支路连接，如图1所示。

高峰期干道拥堵严重，若能在拥堵路段附近组织单行交通，对办公区内部支路进行优化，一方面可以为干道分流，缓解干道的交通压力；另一方面可以提高支路通行能力，增加路侧停车泊位数。

支路双向行车时路侧空间不足以连续设置停车泊位，可于重要建筑物出入口两侧视情况设置部分停车位。而单向行车时在保证同向车道的安全横向距离的条件下，可以减少横向车道间距[4]，条件适宜的情况下(非机动车道连续等)可在道路单侧连续设置停车泊位。

在不影响道路交通流运行情况下，尽可能增加路侧停车泊位数量可以在一定程度上缓解停车供需矛盾。

2 单行交通组织优化双层规划模型

建立以干道路段平均饱和度、车辆绕行系数最小及最大停车泊位增长率为目标的双层规划模型，通过优化单行方案以使目标函数最小；下层模型在单行方案确定的前提下按照用户均衡分配准则进行配流。单向交通组织优化的双层规划具体如下：

对于给定的区域路网N=(V,A∪B)，其中V为区域道路集，A为干道路段集，B为备选支路路段集。记C(a)为路段a的通行能力，a∈A∪B。路段长度为l(a)。交通需求为Qij(n×n)，其中Qij表示从节点i到j的交通流量。

区分道路等级及支路路段的行车方向，通行能力综合表示如下：

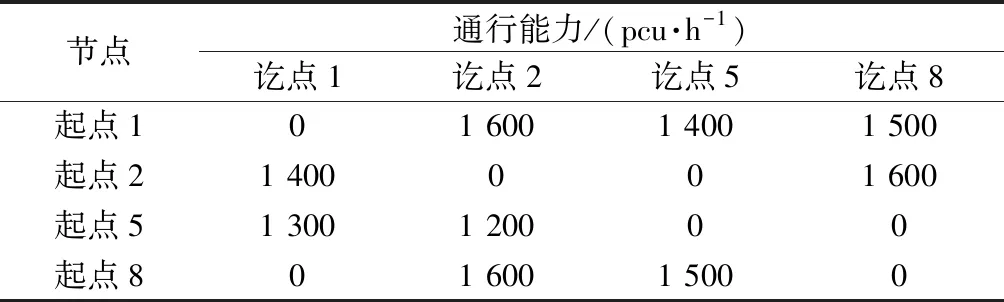
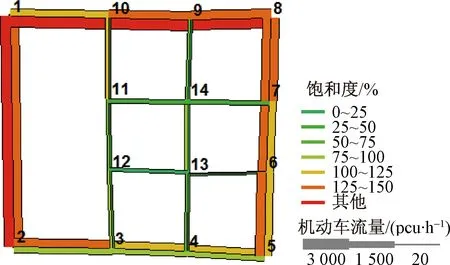
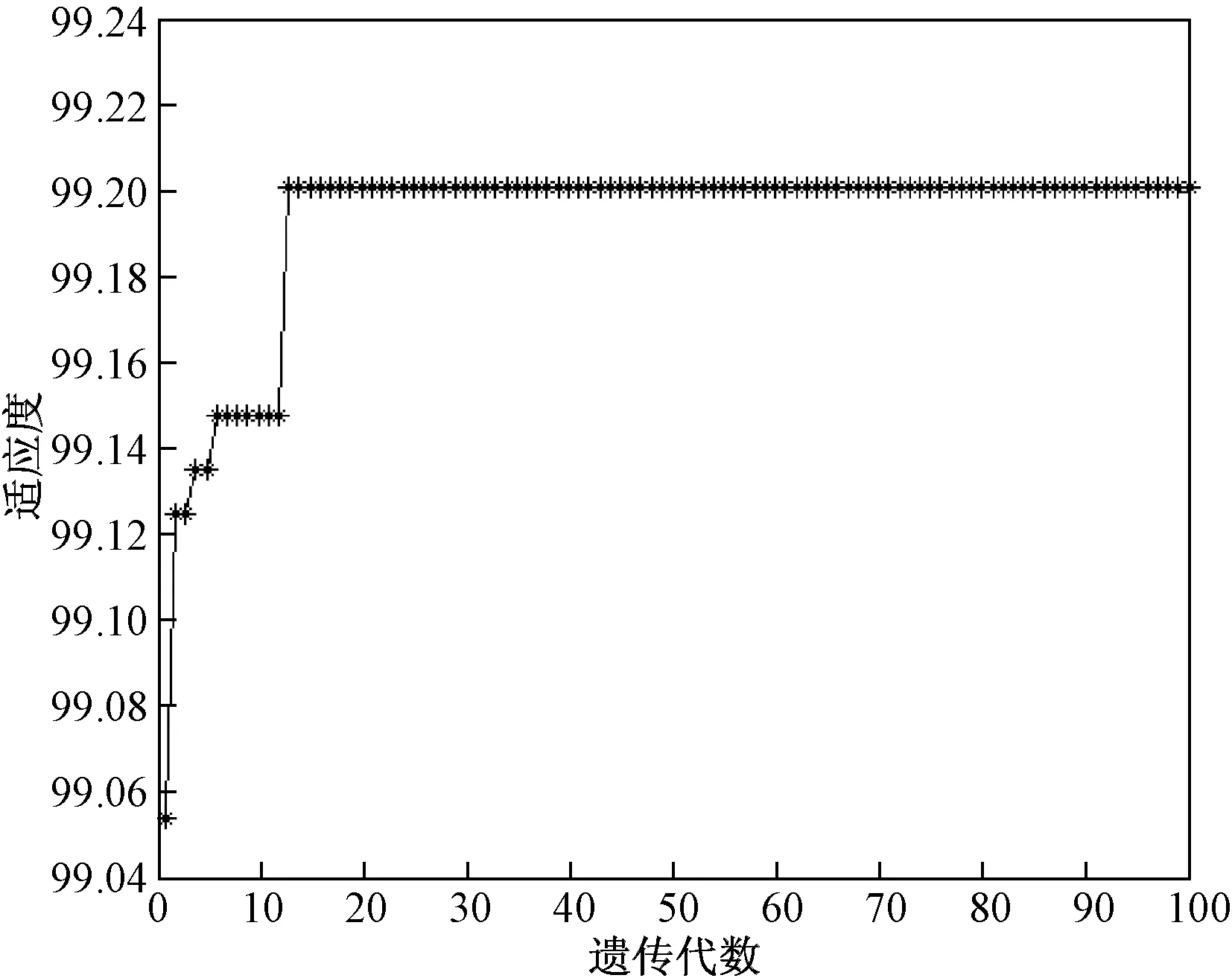
一般情况下，支路路段双向行车时，受对向车流的影响，另一侧通行能力会有所降低，故双向通行能力之和要低于路段单向通行能力，即2C2(a)

记V(a),V(a)∈A∪B为路段a的车流量，则路段饱和度表示为S(a)=V(a)/C(a),a∈A∪B。

记y(a),a∈B为单向决策备选集，a=(vi,vj) 为节点vi至vj之间的无向路段(i

2.1 上层模型

2.1.1 降低干道饱和度

(1)

式(1)中：S(a)表示路段a上的饱和度；l(a)表示路段a的长度。

2.1.2 减少车辆绕行

绕行距离可用实施单行交通后路网内所有车辆的总行驶距离与现有交通组织下车辆的总行驶距离之差表示，组织单行交通后车辆绕行距离系数R的计算公式为

(2)

式(2)中：V(a)表示路段a上的车流量；l(a)表示路段a的长度；V0(a)为现有交通组织下路段a上的交通量。

2.1.3 最大化满足路侧停车需求

支路双向行车时路侧空间不足以连续设置停车泊位，重要建筑物出入口两侧可视情况施化部分停车位。假定支路双向行车时，可设置泊位数为最大泊位数的20%；当支路单向行车时，路侧空间可设置停车带，可施化泊位数为最大泊位数的80%。

假定支路B集中任意路段a=(vi,vj)，平行式停车泊位长度为l(p)，l(a)表示路段a的长度，记路段实际设置的停车泊位数为P(a)，最大泊位数为Pmax(a)=⎣l(a)/l(p)」，计算泊位数时向下取整。

路段实际设置的停车泊位数P(a)可综合表示为

(3)

由此可得，实施单行交通前支路可设置的停车泊位数

(4)

实施单行交通组织后区域内停车泊位增长率

(5)

综上，上层规划为

(6)

(7)

(8)

(9)

V(a)≥0,a∈A∪B(y)

(10)

为上述3个规划目标赋予不同权重参数ξ1、ξ2、ξ3，则上层目标函数为

(11)

2.2 下层模型

在下层模型中，出行者根据上层模型确定的单行交通方案，选择最短路径出行。在路段通行能力的限制下，路段流量可以通过用户平衡配流来获得[12]。

下层模型为

(12)

(13)

(14)

fijk≥0

(15)

式中：f为目标函数，是对各路段的行驶时间积分之后取最小值；fijk为出发地i到目的地j的第k条路径上的交通量；Qij为出发地i到目的地j的交通量；L(i,j)为出发地i到目的地j的路径数；n为i、j的取值上限；δaijk为0-1变量，若路段a属于出发地i到目的地j的第k条路径，则δaijk为1，相反则为0；V(a)为路段a上的交通量；ta[V(a)]为路阻函数。参考文献[13]，拟采用美国联邦公路局函数，即BPR函数。

(16)

式(16)中：ta0为自由流下车辆在路段a的行驶时间(即路段长度与该路段设计速度的比值)；α、β为模型待标定参数，取值分别为0.15、4；Cy(a)为实施单行方案后支路的通行能力，y(a)为0时(即路段a双向行车)，y取值为2，否则y取值为3。

3 模型求解

上层模型确定区域路网的单行交通组织方案，结合下层模型配流结果得到单行交通方案多个优化目标的函数值，采用遗传算法进行求解。Frank-Wolf算法为求解用户均衡模型的经典算法[14]，因此设计嵌套Frank-Wolf算法的遗传算法求解多目标双层规划模型。

下面给出涉及的遗传算法求解步骤。

步骤1 编码。采用实数编码方法，首先对单行交通组织区域内的支路路段进行编号，每一个路段对应染色体中的一个基因位，并根据路段的行车方向来确定相应基因位的编码值，编码值范围为{0，1，-1}。

步骤2 种群初始化。

步骤3 适应度函数定义。在遗传算法中规定适应值为非负，通过Frank-Wolf算法为各个种群对应的道路行车方案分配流量，获得平衡状态下各路段的交通量、饱和度等交通流特征，进而计算每个种群对应的目标函数值，得到每一代种群中的最优(大)适应值。适应度函数定义如下：

(17)

式(17)中:Zmax为Z(y)的最大值估计，Zmax取值为100。

步骤4 选择。采用轮盘赌选择法从既有的群体中选择一些适应度较高的个体来进行交配。假设群体数为n，个体适应度为fi，个体i被选择的概率为

(18)

步骤5 交叉、变异。

步骤6 终止规则。在算法的进化代数达到预先设定的最大迭代次数时，停止迭代，得到对应的最优单行交通组织方案。

4 算例分析

4.1 算例背景

选取北京市海淀区某办公区来进行单行交通组织优化，道路网络如图2所示。

图2 道路网络Fig.2 Road network

图2中四周粗实线表示干道，内部细实线表示支路。交通需求如表1所示。主干道双向的通行能力C1(a)=1 800 pcu/h，次干道双向的通行能力为C1(a)=1 650 pcu/h；支路单向行车的通行能力为C3(a)=1 600 pcu/h，双向行车的通行能力为C2(a)=700 pcu/h。平行式停车泊位长度l(p)=6 m。

根据该区域实际路网及交通环境，路网各条道路的参数如表2所示。

表1 交通需求分布Table 1 Distribution of traffic demand

表2 区域内各路段的主要参数Table 2 Main parameters of roads in the area

4.2 结果分析

在实行单行交通组织前，将表1的交通量分配到路网中可以得到初始干道及支路的交通流量分配结果，如图3所示。

图3 初始路网交通流量分配Fig.3 Traffic distribution of initial road network

未实施单向交通组织前，假定所有支路道路均为双向行车。该区域干道平均饱和度高达130.1%，干道路段最高饱和度为174.1%，干道交通拥堵严重。同时区域内支路平均饱和度为24.3%，利用率较低。

实施单向交通组织优化时，权重系数取值分别为ξ1=0.5、ξ2=0.35、ξ3=0.15。本文算法采用MATLAB R2014a实现，求解算法的基本参数赋值如下：初始种群取80，交叉率取0.6，变异率取0.1，设定进化代数为100。

随着进化代数的增加，最大适应度值的变化趋势如图4所示。在20代以前，收敛速度较快，当迭代至20代起，最大适应度值明显趋于稳定，表明种群已经成熟，算法收敛性较好。优化后得到支路行车方案对应的路网拓扑结构如图5所示。

图4 最优适应度与遗传代数关系Fig.4 Diagram of optimal fitness and genetic algebra

组织单行交通后，各路段流量及饱和度如图6所示。优化前后部分典型路段(支路)可设置的停车泊位数如表3所示。进行单行交通组织后，干道平均饱和度为115.2%，支路饱和度变为53.3%。相比未组织单行交通，干道饱和度降低14.9%，支路饱和度增大了29%，道路服务水平明显提高。

由图3、图6可以看出，经过优化交通流量在路网中的分布更加均衡，干道拥堵有所缓解，支路利用率显著提高。同时，组织单行交通引起的车均绕行距离仅为5.8 m，同时支路可增设路侧停车泊位98个，相较单行交通组织前增加288%，可在一定程度上缓解办公区的停车供需矛盾。

图5 优化后路网拓扑结构Fig.5 Optimized road topology

图6 优化后交通流量分配Fig.6 Optimized traffic flow distribution

表3 优化后部分支路停车泊位数对比Table 3 Comparison of parking berths of some branches after optimization

对于支路网络，组织单行交通可以达到为干道交通分流的目的，但优化潜力有限，干路饱和度无法绝对下降到某一水平，可以看到优化后小部分干道的饱和度依旧大于1，对此可以通过道路改扩建来进一步优化。

5 结论

从道路负荷度、车辆绕行以及路侧停车需求三方面出发，提出了针对城市办公区路网的单向交通组织的双层规划模型，并采用嵌套Frank-Wolf算法的多目标遗传算法求解模型，并通过算例对比了单行交通组织前后各路段的流量、饱和度及绕行时间等指标，得到以下结论：

(1)实施区域单行交通组织后，道路网内部交通压力的时空分布得到均衡，具体表现为干路平均饱和度下降，支路饱和度增大了29%，支路利用率得到显著提升。

(2)与既有研究相比，本文模型的建立考虑了城市办公区路侧停车需求因素，同饱和度、绕行影响叠加后确定了单行交通组织优化方案。通过算例对比，单行交通组织后，支路可增设的路侧停车泊位为实施单行交通组织前的2.9倍。

通过算例验证，本文模型确定单行交通组织方案具有一定优势，可为办公区等停车供需矛盾突出的城市中心区域组织单行交通提供理论支持。但在交通流量分配中采用了传统的用户均衡分配模型，流量分配过程未受到路段容量限制，进一步研究有容量约束的分配模型可以实现更加符合实际的交通流量分配。