高原机场着陆性能计算与分析

潘 军， 陈柏松， 华 欣

(空军航空大学航空作战勤务学院，长春 130022)

飞机的每一次飞行过程都是以起飞开始，以着陆结束[1]。起飞和着陆过程是飞行中最高危的阶段。着陆过程和起飞过程相比，完成难度更大，着陆性能的研究一直是飞行性能研究的热点。

高原机场是指海拔在1 500 m以上的机场[2]，高原环境恶劣，空气稀薄，对着陆过程影响很大，由于高原机场飞机接地速度不同，会极大地影响刹车摩擦系数的使用规律，进而影响着陆滑跑距离。现有的着陆滑跑摩擦系数估算方法主要有：用定值估计平均摩擦系数的折算摩擦系数法[3]；对起落架系统进行详细建模，根据起落架系统的特点确定刹车摩擦系数的起落架力学模型法[4]；对于有自动刹车系统的飞机，还可以根据加速度自动控制的情况，推算出对应加速下的刹车摩擦系数[5]。这些方法多是停留在平原机场的基础上，高原机场着陆速度大，滑跑距离长，传统方法不适合高原机场。为此，结合高原机场特点，提出了利用飞参数据反推的确定刹车摩擦系数的方法，验证了方法的准确性和实用性。分析了不同条件对着陆滑跑距离的影响，给出了相关曲线，以期为高原机场着陆提供参考。

1 着陆过程

飞行员做好着陆前准备，对准方向，下降高度，从安全高度开始，经过空中直线下滑，拉平，接地滑跑，直到完全停止的全过程被称为着陆。从安全高度开始下滑到完全停止这段过程经过的水平距离称为着陆距离[6]。着陆过程主要分为3个阶段[7]，如图1所示。

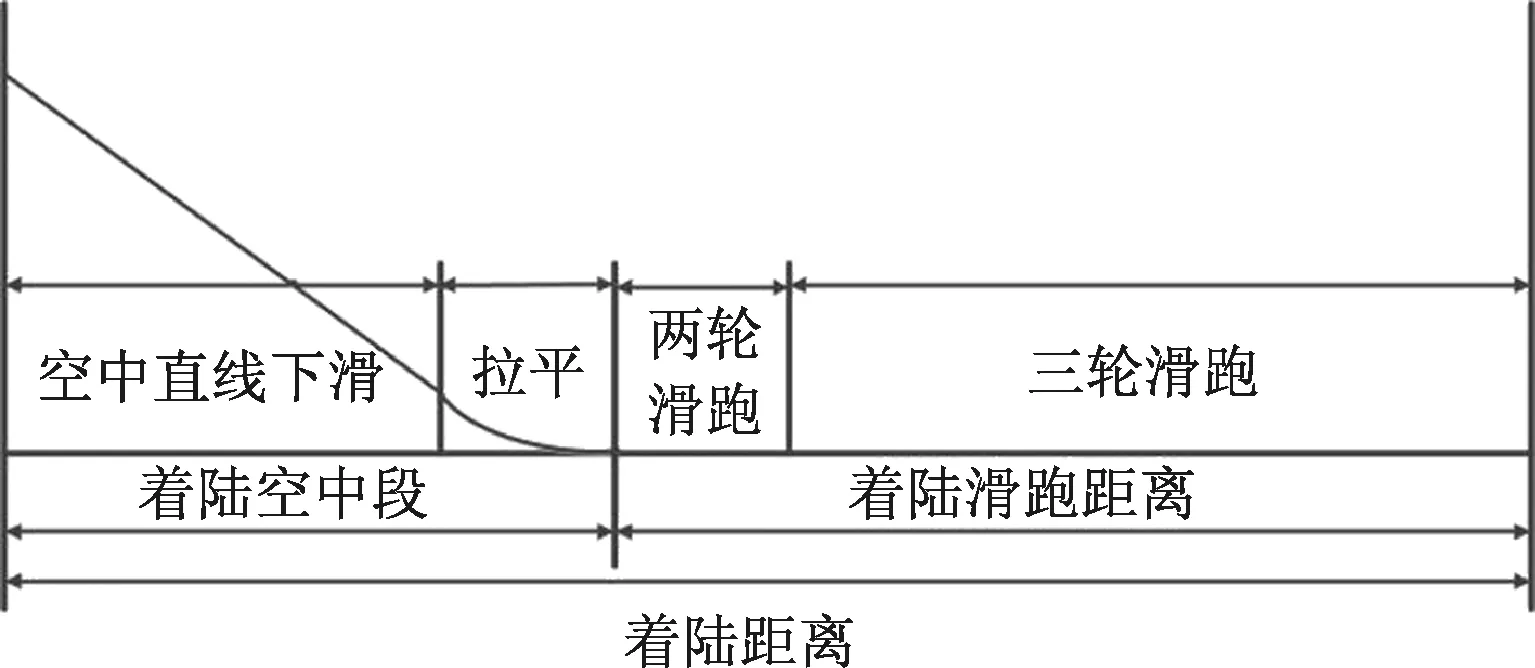
图1 飞机的着陆过程Fig.1 Landing process of aircraft

(1)空中直线下滑。飞机从安全高度(一般是25 m)[8]开始，以某一下滑角下滑(一般为-3°)，直到下滑到拉平高度，空中直线下滑段结束。

(2)拉平。拉平过程中，飞机速度减小，迎角增大，飞机的下降率进一步减小，为飞机接地做好准备。

(3)接地滑跑。飞机以某一着陆迎角接地，首先是主轮接地，进入两轮滑跑，之后经过一段时间，前轮接地，进入三轮滑跑。随着速度进一步减小，使用刹车使飞机迅速减速，直到飞机的滑跑速度减小到零。飞机从接地开始滑跑到停止到跑道上的这段水平距离，称为着陆滑跑距离。

2 着陆过程计算模型

着陆3个阶段运动情况存在较大的差异，按着陆3个阶段不同特点，对着陆过程进行建模[9]。

2.1 空中直线下滑段

飞机在直线下滑段受到重力、气动力、发动机推力的作用，将飞机受到的合外力集中到飞机的质心上，可以得到空中直线下滑段满足的方程为

(1)

式(1)中：

(2)

(3)

m为飞机质量；V为飞机的空速；t为时间；n为发动机的台数；P为单台发动机的推力，其值为马赫数与高度的函数，着陆过程中，发动机一般处在慢车状态，其值可由发动机推力特性插值得到[10-12]；α为飞行迎角；φP为发动机安装角；g为重力加速度；D为飞机受到的气动阻力；γ为下滑轨迹角，一般取-3°；L为升力；H直线下滑为直线下滑段的高度变化量；S直线下滑为直线下滑段的水平距离；CL为升力系数，CD为气动阻力系数，其值均可由升阻特性插值得到[13]；ρ为空气密度；Ma为马赫数。

2.2 拉平段

拉平段经历的时间很短，将其简化为匀速圆周运动，根据圆周运动的特点，在下滑轨迹角γ不大的情况下，可以列出拉平段满足的方程为

(4)

从式(4)可得

(5)

式中：R为将拉平阶段简化为圆周运动的运动半径；H拉平为直线下滑段的高度变化量；S拉平为直线下滑段的水平前进距离；G为飞机重力。

2.3 地面滑跑段

地面滑跑段受力如图2所示。

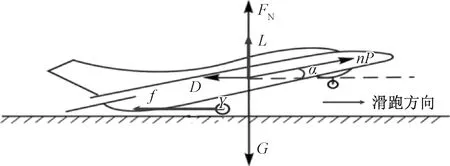
图2 地面滑跑段受力Fig.2 Forces on the ground taxiing section

地面滑跑段满足的力学方程为

(6)

式(6)中：

(7)

式(7)中：V地表示飞机滑跑地速；V风表示沿滑跑方向的风速；f表示地面给机轮的摩擦阻力；μ表示跑道摩擦阻力系数，对于干水泥跑道，不刹车时取0.03[3]；FN表示地面支持力。

2.3.1 两轮滑跑段

认为接地瞬间飞机的升降率为0，根据力的平衡求出接地速度，假设主轮接地迎角为α主轮接地，接地迎角对应的是接地升力系数CL主轮接地，可以得到平衡方程：

(8)

由式(8)可得：

(9)

式(9)中：V主轮接地表示飞机主轮接地时的空速。

两轮滑跑段中，假设两轮滑跑过程时间为3 s，这段时间里飞机迎角逐渐减小直至前轮接地，并认为迎角与速度是线性变化的，迎角变化规律为[14]

α主轮接地

(10)

式(10)中：α两轮表示两轮滑跑时的迎角；V前轮接地表示飞机前轮接地时的空速；α前轮接地表示前轮接地时的迎角，认为前轮接地时的迎角就是飞机的停机迎角α停机，有如下关系：

α前轮接地=α停机

(11)

从主轮接地到前轮接地这段时间里，滑跑速度变化规律为

(12)

式(12)中：t主轮接地表示主轮接地的时刻;t为两轮滑跑的时间。

于是可以得到两轮滑跑阶段经过的总距离

S两轮=

(13)

式(13)中：S两轮表示两轮滑跑阶段的滑跑距离；FN两轮表示两轮滑跑时的地面支持力；CD两轮表示两轮滑跑迎角对应的气动阻力系数。

2.3.2 三轮滑跑段

三轮滑跑过程中，滑跑迎角满足如下关系式：

α三轮=α停机

(14)

结合式(6)和式(7)，可以得到三轮滑跑过程经过的滑跑距离为

S三轮滑跑=

(15)

式中：α三轮表示三轮滑跑的迎角；S三轮滑跑表示三轮滑跑阶段的滑跑距离；FN三轮表示三轮滑跑时的地面支持力；CD三轮表示三轮滑跑的气动阻力系数。

3 高原机场着陆性能计算方法

高原机场着陆性能计算的关键在于建立高原大气环境模型和确定刹车摩擦系数。

3.1 大气环境模型

高度H处声速：

(16)

高度H处密度：

ρH=ρ0(1-2.255 77×10-5H)4.255 88

(17)

高度H处温度：

TH=T0-0.006 5H

(18)

高度H处压强：

PH=P0(1-2.255 77×10-5H)5.255 88

(19)

海平面处各个大气参数为a0=340.294 m/s，ρ0=1.225 0 kg/m3，T0=288.15 K，P0=101 325 Pa。

3.2 折算摩擦系数法

为了验证折算摩擦系数法的精度，以某型飞机为例，折算摩擦系数按干水泥跑道的经验值选取为0.3[3]，在给定的计算条件下，将计算结果与飞行手册数据比较，结果如表1所示。

表1 折算摩擦系数法计算精度Table 1 Accuracy of converted friction coefficient method

注：绝对误差等于仿真值与手册值之差，相对误差等于绝对误差除以手册值。

从表1可以看出，折算摩擦系数法的结果与手册中得出的结果有较大误差，所以折算摩擦系数法并不能满足精度要求。

3.3 基于飞参数据确定刹车摩擦系数

从表1中的仿真结果可以看出，按折算摩擦系数得到的结果是不够准确的。为此提出利用飞参数据反推，确定刹车系数变化规律的方法，步骤如下：

(1)建立飞机滑跑阶段的动力学模型，根据飞参数据记录的飞机滑跑速度，求导得到不同时刻沿滑跑方向的加速度，并将沿滑跑方向的加速度和速度的关系进行拟合，得到沿滑跑方向的加速度a随速度变化而变化的关系式a=f3(V)。

(2)利用力的平衡法，结合式(6)求出不同时刻作用在机轮上的摩擦力大小。

(3)根据式(7)求出跑道给飞机的支持力，根据摩擦系数计算公式，求出摩擦系数。

(4)以滑跑迎角和滑跑速度为自变量，摩擦系数为因变量，就可以得到刹车摩擦系数与迎角及滑跑速度之间的关系，由式(6)、式(7)可得：

(20)

拟合曲线，就可以得到刹车摩擦系数μ随速度变化的函数关系式μ=f4(V)。

3.4 改进模型验证

在与表1相同的条件下计算，结果如表2所示。

表2 改进后的模型计算精度Table 2 Accuracy of the improvement method

从表2中可以看出，对刹车摩擦系数进行改进后，在相同条件下最大误差值从6.7%降到了2.0%，精度有了明显提高。说明改进后的刹车摩擦系数确定方法更加贴近实际。该方法避免了如文献[15]中将空气阻力折合到摩擦阻力中方法带来的误差，也免去了考虑不同刹车位置的麻烦。

4 高原机场着陆滑跑距离分析

高原机场环境特殊，选取着陆性能中的着陆滑跑距离为研究对象，分析单一因素改变对着陆滑跑距离的影响，并给出相关曲线。

4.1 海拔高度对着陆滑跑距离的影响

计算条件：以某型飞机为算例，无外挂标准着陆构型进行着陆滑跑，跑道无坡度、无风，着陆全程按标准操纵动作操纵，不打开减速板，刹车摩擦系数按某型飞机飞参显示的刹车摩擦系数选取，发动机双发慢车状态工作，气温为15 ℃，飞机的滑跑迎角与发动机安装角均为0°，着陆接地迎角为10°，着陆质量为7 300 kg。着陆滑跑距离与海拔高度的关系如图3所示。

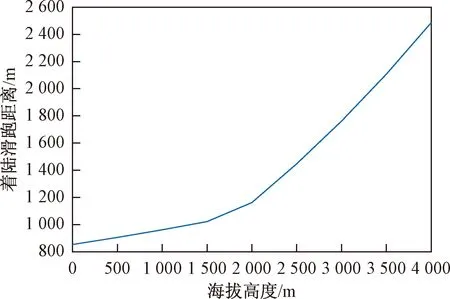
图3 着陆滑跑距离与海拔高度的关系Fig.3 Relationship between landing taxiing distance and altitude

从图3可以得出，海拔高度增加，着陆滑跑距离增长。其他条件不变，海拔高度升高时，曲线斜率会明显增加。这主要是因为海拔高度高，飞机的着陆接地初速度大于允许使用刹车的最大滑跑速度，使得接地初始阶段飞机不能很快减速，造成滑跑距离大大增加。海拔高度在0～1 000 m变化时，高度每增加100 m，滑跑距离只增加约11 m；海拔高度在2 000～4 000 m变化时，高度每增加100 m，着陆滑跑距离增加约66 m。

4.2 质量对着陆滑跑距离的影响

计算条件：其余条件不变，着陆质量在5 800～7 400 kg变化。着陆滑跑距离与质量的关系如图4所示。

图4 着陆滑跑距离与着陆质量的关系Fig.4 Relationship between landing taxiing distance and mass

从图4可以得出，随着着陆质量增大，着陆滑跑距离增加。海拔高度升高会增大着陆质量对滑跑距离的影响。海拔高度在2 000 m以下，着陆质量每增加100 kg，着陆滑跑距离增加约10 m；海拔为3 000 m时，着陆质量每增加100 kg，着陆滑跑距离增加约60 m；海拔为4 000 m时，着陆质量每增加100 kg，着陆滑跑距离要增加约70 m。海拔高度为2 000 m与3 000 m时，曲线斜率存在一个拐点，这是因为拐点时接地速度大于最大允许刹车速度导致的。海拔2 000 m时，拐点对应质量约为7 100 kg；海拔3 000 m时，拐点对应的质量约为6 200 kg；海拔2 000～3 000 m时，拐点质量介于二者之间。

4.3 温度对着陆滑跑距离的影响

计算条件：其余条件不变，机场温度在-30～50 ℃变化。着陆滑跑距离与温度的关系如图5所示。

图5 着陆滑跑距离与温度的关系Fig.5 Relationship between landing taxiing distance and temperature

从图5可以得出，随着温度升高，着陆滑跑距离增加。随着高度增加，着陆滑跑距离受温度的影响更为显著。高度1 000 m以下，温度每增加10 ℃，着陆滑跑距离增加约25 m；海拔3 000 m时，温度每增加10 ℃，着陆滑跑距离增加约146 m；海拔为4 000 m时，温度每增加10 ℃，着陆滑跑距离增加约174 m。2 000 m高度的曲线出现了拐点，对应的是接地速度约等于允许使用刹车的最大滑跑速度。

4.4 风速对着陆滑跑距离的影响

计算条件：其余条件不变，沿滑跑方向的风速在-8～8 m/s变化，顺风风速为负值，逆风风速为正值，着陆滑跑距离与风速的关系如图6所示。

图6 着陆滑跑距离与风速的关系Fig.6 Relationship between landing distance and wind speed

从图6可以得出，逆风风速增加，着陆滑跑距离缩短。海拔高度增加会增大风速变化对着陆滑跑距离的影响程度。海拔高度为0 m，逆风每增加1 m/s，着陆滑跑距离缩短约22 m；海拔3 000 m以上时，逆风每增加1 m/s，着陆滑跑距离缩短约100 m。高度1 000 m的着陆滑跑距离曲线拐点出现在顺风4 m/s处，高度2 000 m的着陆滑跑距离曲线拐点出现在逆风2 m/s处，拐点附近对应的着陆接地速度约为允许使用刹车的最大滑跑速度。

4.5 着陆接地迎角对着陆滑跑距离的影响

计算条件：其余条件不变，主轮接地时的着陆迎角在6°～12°变化。着陆滑跑距离与着陆接地迎角的关系如图7所示。

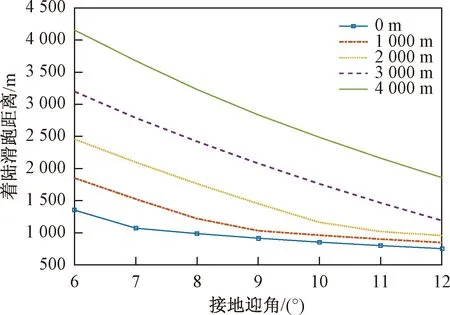
图7 着陆滑跑距离与接地迎角的关系Fig.7 Relationship between landing taxiing distance and AOA

从图7可以得出，着陆接地迎角增加，着陆滑跑距离缩短。随着高度增加，着陆滑跑距离受接地迎角的影响变得更显著。海拔高度为0 m，接地迎角每增加1°，着陆滑跑距离缩短约63 m；海拔4 000 m时，接地迎角每增加1°，着陆滑跑距离减少约382 m。3 000 m以下的各个高度的曲线出现了拐点，其接地速度对应允许使用刹车的最大滑跑速度。

4.6 最大刹车使用对着陆滑跑距离的影响

计算条件：其余条件不变，最大刹车压力在25%～100%变化。着陆滑跑距离与最大刹车压力的关系如图8所示。

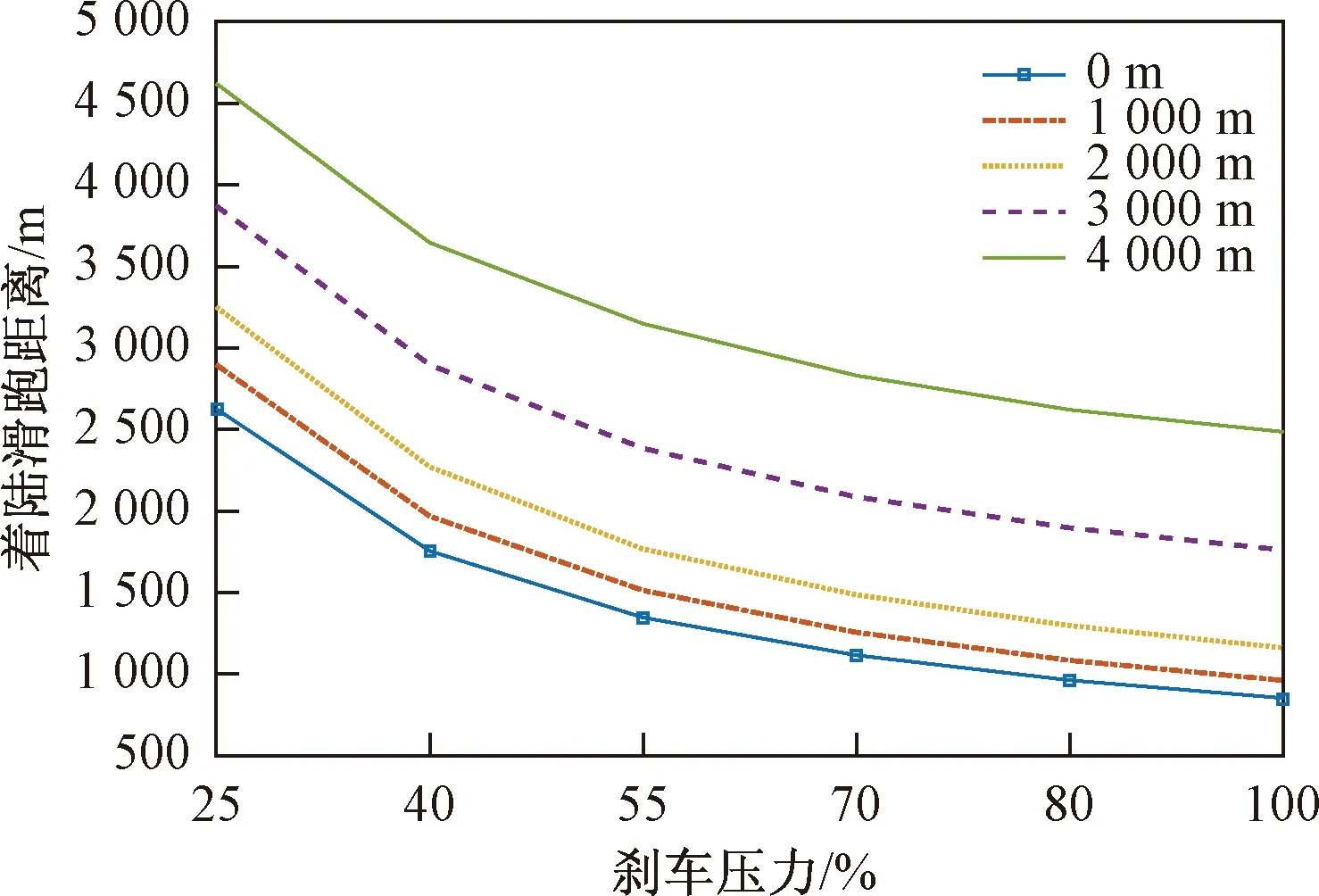
图8 着陆滑跑距离与最大刹车压力的关系Fig.8 Relationship between landing distance and maximum braking pressure

从图8可以得出，最大刹车压力大，刹车摩擦系数就大，飞机就能以更快的速度停止滑跑。随着刹车压力增大，着陆滑跑距离随最大刹车压力变化的曲线斜率减小。最大刹车压力相同的情况下，高度升高，着陆滑跑距离相应增加，且高度越高增加速度越快。

5 结论

根据飞机着陆过程的特点，将着陆分为空中直线下滑、拉平和地面滑跑3个阶段，把地面滑跑分为了两轮滑跑和三轮滑跑。分析了不同阶段的受力情况，建立了运动方程，构建了着陆性能的计算模型，提出了基于飞参数据确定刹车摩擦系数的方法，分析了海拔高度、飞行质量、温度、风速、着陆迎角和最大刹车压力之间的关系，给出了相关曲线，得出以下结论：

(1)利用飞参数据反推确定着陆滑跑过程的刹车摩擦系数的方法是可行的，该方法能够减小传统方法的误差，使刹车摩擦系数更贴近实际。

(2)高度增加会加大其他因素对着陆滑跑距离的影响程度。在高原机场着陆时，应选择大迎角、小质量逆风接地，以尽可能缩短着陆滑跑距离，最大限度保证飞行安全。