剪式铰可展开圆环设计、仿真与试验

梁浩 王立武 唐明章 朱谦 刘媛媛

剪式铰可展开圆环设计、仿真与试验

梁浩 王立武 唐明章 朱谦 刘媛媛

（北京空间机电研究所，北京 100094）

随着航天技术的迅猛发展，航天设备的尺寸也越来越大，以至于很多航天设备难以装入运载器的包络内。而可展开结构是克服内包络限制的有效手段，剪式铰作为一种传统的可展开单元，通过设计可形成多种可展开结构，具有广阔的应用前景。但剪式铰可展开结构往往零件众多，采用传统有限元计算模态往往需要大量的时间无法快速迭代，等效刚度法是一种快速的计算方法。文章针对空间相机遮光罩设计了一种可展开圆环结构，采用等效刚度法计算了其一阶基频，并进行了试验验证。结果表明采用等效刚度法能大大减小有限元网格规模和复杂程度，能够实现快速设计迭代，且计算精度在4%以内。

剪式铰 等效刚度法 可展开结构 正弦振动 遮光罩 空间相机

0 引言

随着航天技术的迅猛发展，航天设备的尺寸也越来越大，以至于很多航天设备难以装入运载器的包络内，如太阳能翼板、雷达天线阵列、机械臂、空间桁架等，不得不以折叠压缩状送入太空，到达预定轨道后再展开为所设计的几何构形，可展开结构目前在航天领域已被广泛应用且具有广阔的应用前景[1]。而可展开结构的设计，既含有结构设计、机构综合，又具有重要的结构工程学特征，是一项复杂的设计过程，如“詹姆斯·韦伯”太空望远镜（James Webb Space Telescope，JWST）其主镜、次镜均采用了折叠收拢设计，展开收拢需考虑体积约束、可靠性约束及性能指标约束，研制技术难度大，目前研制费用已达87亿美元，发射周期也推至2020年[2-3]。可展开结构往往含有较多零件，但零件重复性较高，在仿真计算时网格较多，仿真计算过程缓慢，难以形成快速迭代，如ETS-VIII卫星[4]、Thuraya可展天线[5]等等均有大量相同零件，等效刚度法能大大减小有限元网格规模和复杂程度，主体思路为将零件简化等效到一个刚度相同的梁单元上，再进行阵列，使其具有相同的力学性能，之后再使用有限元方法进行计算，是一种有效的计算方法[6]。

随着分辨率的提高，空间相机的尺寸也越来越大，为满足整流罩包络需求，其遮光罩往往采用折叠展开形式，而可展开结构是可展开遮光罩的研究基础，本文设计了一种可展开圆环，用等效刚度法对其进行了仿真计算，并采用正弦扫频试验对仿真结果进行验证。正弦振动试验是一种常用的航天设备可靠性试验方法，是在实验室中模拟真实环境中因振动、旋转、脉冲等产生的正弦振动，从而检验产品的可靠性与耐久性的一种环境试验[7]。而正弦扫频试验则用于判断产品共振频率：是指在试验过程中维持一个或两个振动参数（位移、速度或加速度）量级不变，而振动频率在一定范围内连续往复变化的试验。在力学振动环境试验中，常以正弦－随机振动疲劳等效的方法用正弦扫频试验来代替,模拟宽带随机振动试验或瞬态冲击试验[8-9]。

1 可展开圆环结构设计

可展开圆环结构，是一种可实现径向展收的圆形结构，其设计要点为质量轻、结构紧凑、空间环境适应性好和可靠性高，特殊场合可能需要具有高精度、高刚度及高稳定度。目前，大型可展开结构的几何设计，大都采用先进行单元设计、再由基本单元组合成完整结构的方法，否则很难保证整体结构的可展性[10]。

根据上述要求，设计了一种剪式铰可展开圆环：通过剪式铰角度的变化，实现可展开圆环尺寸的变化。单组剪式铰[11]几何结构简图如图1所示。

图1 有折角剪式铰几何结构

图1中，、为两根折杆，两根杆的折角∠=∠=，且有长度关系

==1，==2（1）

两根杆间的夹角为∠=，为单元展开程度的参数。

根据图1，

则

直线的方程为

式中 (x, y)和(x, y)为点，在图1（a）中的坐标；为直线的斜率。

将点和的坐标代入式(4)可得

最终得到

式（6）表示只有当杆和的折角与剪式铰单元对应的圆心角之和为π时，该圆形可展开结构能够展开。

点坐标，通过同样方法表示为

点和点之间距离即为环形可展开骨架半径，设1=2，则

通过式（6）确定的关系式及作图法即可初步计算剪式铰臂长及可展开圆环剪式铰单元的数量：用CAD软件作图，画3个圆，直径分别为所需值（收拢后内径为1 200mm，展开后外径3 400mm，展开后内径3 300mm），并过圆心画夹角为特定度数的两条直线，通过几何关系即可初步得到臂长，及所需剪式铰单元数量。

最终取剪式铰单元数量为36组，则=170°，并取整得====150mm。

通过结构设计，限制机构展开后外径3400mm，收缩后外径1200mm，则最终状态圆环展开收拢比

3400mm/1200mm=2.83 （9）

同时为使环向可展开结构具有较高的抗拉、抗弯刚度及较轻的质量，主体结构设计为变截面工字梁构型[12]，如图2。为使其具有高可靠性、高精度及高环境力学能力，转动处采用了角接触轴承来抗振动环境，公差间隙为经验值，配合间隙[13]取H9/d9，实际产品如图3。

图2 工字梁剪式铰单元

图3 可展开圆环三维模型

2 等效刚度模型建立

2.1 等效刚度法原理与方法

针对等截面梁的计算，通过查阅机械设计手册可很快得到计算方法。而在航天产品设计中为了获得较高的刚度以及较轻的质量，其往往是变截面的，变截面梁没有现成公式可以直接进行计算，采用有限元计算[14]时，由于结构的复杂性，其网格规模较大，计算时间较长。而在可展开结构设计时，由于其含有大量重复复杂单元，计算难度更大。采用等效刚度法是一种易于工程设计人员掌握的有效方法[15-18]。

如本文所设计的剪式铰单元本质为一变截面悬臂梁，其截面连续变化，任一截面惯性矩为I，为将其等效为刚度相同的等截面梁，根据两梁弯曲应变能相同的原理，即可建立如下等式

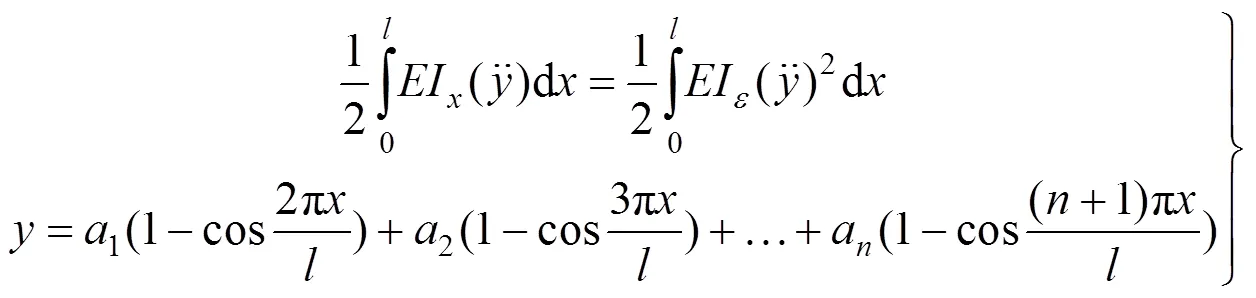
式中为弹性模量；I为变截面梁任一截面惯性矩；I为刚度相同等截面梁的惯性矩；为悬臂梁挠度曲线方程[19]；为梁的长度，0~；a为位移参数，=1，2，…，。

求解即得变截面梁的惯性矩与等截面梁惯性矩之间的关系，进而求得等截面梁惯性矩。通过该理论可知，等效刚度法计算是完全可行的，可扩展在有限元计算上，即在剪式铰单元结构改变时，只需要调整等效模型的截面参数，无需重新建立有限元模型，即可得到结果，应用该方法可增强有限元模型的参数化功能同时大量减少网格数量，提高计算效率[20-22]。

2.2 建立等效刚度模型

在仿真软件中通过等效刚度法，首先建立两个150mm长的梁单元，设其夹角为170°，并约束两梁单元端部的6个自由度，即固支约束；其次以同样的方法建立另两根150mm的梁单元，并建立约束，选择两个单元的中端，约束其5个自由度，仅放开其旋转自由度，成为铰接约束[23]。通过组合体的左右端点建立圆心，并以圆心整列组合体，最终得到所需可展开圆环模型，调整两单元夹角即可得到不同尺寸的可展开圆环模型，计算方法见式(8)。

赋予梁单元工字梁截面，并在各销轴节点处通过质量点的形式将轴承及螺钉质量赋予仿真模型，计算单组梁单元的基频及变形量，通过与实体单组模型仿真结果对边，调整工字梁参数，最终得到的等效刚度模型如图4所示。

图4 环向梁单元结构截面等效

按此方法，建立了简化环向梁模型，边界条件为约束圆环均布在90°方向4点的六个自由度，在展开内径为361 mm、672 mm、1 062 mm时计算了其一阶基频[24]，仿真结果见图5。在不同展开内径条件下其振型均为以圆环1/4为支点，圆环1/8处上下摆动，基频分别为11.545 Hz，8.735 Hz，6.997 Hz，随着展开内径的增大基频逐渐减小。

3 试验验证

在上述设计和仿真结果的指导下，加工可展开圆环模型并进行轴向扫频验证试验，现场安装状态如图6所示。同时在可展开圆环及振动试验台上布置加速度传感器，与试验台连接点和加速度传感器粘贴位置见图6。所用试验仪器为ES-100-550振动试验台，对可展开圆环进行0.2n正弦扫频试验。

图6 正弦扫频试验安装图

通过加速度传感器可获得试验数据，试验第一个加速度峰值即为可展开结构的1阶固有频率[25-27]，如图7所示。

图7 展开内径361，672，1 062 mm时扫频试验数据

试验结果表明，随着可展开结构的逐渐展开，一阶基频逐渐降低，变化趋势与仿真相同，仿真数据与试验数据对比如表1所示。

表1 扫频试验结果与仿真数据对比

Tab.1 Comparison of sweep test results & simulation data

经过试验数据比较发现，仿真与试验数据相近，基频相对误差均在4%以内，说明采用等效刚度法进行仿真结果是可靠的。

4 结束语

本文以剪式铰单元为核心可展开元件设计了一种可展开圆环结构，采用等效刚度法对其一阶固有频率进行了仿真计算，并进行了扫频试验验证。通过对比扫频试验数据与仿真计算结果，得出以下结论：

1）等效刚度法大大减小了有限元网格规模和复杂程度，且利于调整等效单元的刚度参数，能够实现快速设计迭代；

2）等效刚度法与扫频试验结果基频数据基本一致，相对误差在4%以内，说明采用等效刚度法进行仿真计算是可行的。

[1] 曹长明. 星载可展开结构若干关键技术问题的研究[D]. 杭州: 浙江大学, 2016.CAO Changming. Research on Some Key Technical Problems of on-board Deployable Structure[D]. Hangzhou: Zhejiang University, 2016. (in Chinese)

[2] MAGLIONE P. Very High Resolution Optical Satellites: An Overview of the Most Commonly Used[J]. American Journal of Applied Sciences, 2016, 13(1): 91.

[3] 朱仁璋, 丛云天, 王鸿芳, 等. 全球高分光学星概述[J]. 航天器工程, 2015, 24(6): 85-106. ZHU Renzhang, CONG Yuntian, WANG Hongfang, et al. Overview of Global High Resolution Optical Stars[J]. Spacecraft Engineering, 2015, 24(6): 85-106. (in Chinese)

[4] MEGURO A, SHINTATE K, USUI M, et al. In-orbit Deployment Characteristics of Large Deployable Antenna Reflector Onboard Engineering Test Satellite VIII[J]. Acta Astronautica, 2009, 65(9-10): 1306-1316.

[5] THOMSON M W. The AstroMesh Deployable Reflector Antenna[J]. IEEE Antennas and Propagation Society International Symposium. 1999, 3: 1516-1519.

[6] 应玲君, 赵荣珍, 马德福, 等. 基于动态等效刚度的平面柔性铰链建模与分析[J]. 振动与冲击, 2019, 38(3): 222-228. YING Lingjun, ZHAO Rongzhen, MA Defu, et al. Modeling and Analysis of Planar Flexure Hinge Based on Dynamic Equivalent Stiffness[J]. Vibration and Impact, 2019, 38(3): 222-228. (in Chinese)

[7] 欧阳星, 余雄庆, 王宇. 采用等效刚度有限元模型的复合材料机翼颤振分析[J]. 振动工程学报, 2015, 28(3): 404-410.OUYANG Xing, YU Xiongqing, WANG Yu. Flutter Analysis of Compliant Wing Using Equivalent Stiffness Finite Element Model [J]. Journal of Vibration Engineering, 2015, 28(3): 404-410. (in Chinese)

[8] 张步云, 陈怀海, 贺旭东. 多输入多输出正弦扫频试验控制新方法[J]. 振动与冲击, 2015, 34(8): 192-202.ZHANG Buyun, CHEN Huaihai, HE Xudong. A New Control Method of Multi Input and Multi Output Sine Sweep Frequency Test [J]. Vibration and Shock, 2015, 34(8): 192-202. (in Chinese)

[9] 杨巍. 多输入多输出正弦扫频试验控制方法研究与实现[D]. 南京: 南京航空航天大学, 2011.YANG Wei. Research and Implementation of Multi Input and Multi Output Sinusoidal Sweep Test Control Method[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2011. (in Chinese)

[10] 刘锡良. 现代空间结构[M]. 天津: 天津大学出版社, 2003. LIU Xiliang. Modern Spatial Structure[M]. Tianjin: Tianjin University Press, 2003. (in Chinese)

[11] GANTES C. Geometric Design of Arbitrarily Curved Bi. Stable Deployable Arches with Discrete Jointsize[J]. International Journal of Solids and Structures, 2004, 41: 5517-5540.

[12] 朱群红. 简支楔形变截面工字钢梁的弹性弯扭屈曲[D]. 杭州: 浙江大学, 2004.ZHU Qunhong. Elastic Flexural Torsional Buckling of Simply Supported Tapered I-beams[D]. Hangzhou: Zhejiang University, 2004. (in Chinese)

[13] 赵艳平, 魏康, 谈蕊. 轴承组件配合问隙的数字化公差分析[J]. 轴承, 2013(2): 10-13.ZHAO Yanping, WEI Kang, TAN Rui. Digital Tolerance Analysis of Bearing Assembly Fit Clearance[J]. Bearing, 2013(2): 10-13. (in Chinese)

[14] 陈向阳. 可展桁架结构展开过程和动力响应分析及结构设计[D]. 杭州: 浙江大学, 2000. CHEN Xiangyang. Development Process, Dynamic Response Analysis and Structural Design of Deployable Truss Structure[D]. Hangzhou: Zhejiang University, 2000. (in Chinese)

[15] 陈金龙, 吴君正, 张能辉. 开孔变截面微悬臂梁传感器的等效刚度和固有频率[J]. 传感技术学报, 2017, 3 (9): 1324-1329.CHEN Jinlong, WU Junzheng, ZHANG Nenghui. Equivalent Stiffness and Natural Frequency of Micro Cantilever Sensor with Variable Cross Section and Opening[J]. Journal of Sensing Technology, 2017, 3 (9): 1324-1329. (in Chinese)

[16] 应玲君. 多自由度平面柔性铰链的动态等效刚度计算方法研究[D]. 兰州: 兰州理工大学, 2018.YING Lingjun. Study on the Calculation Method of Dynamic Equivalent Stiffness of Multi Degree of Freedom Planar Flexure Hinge[D]. Lanzhou: Lanzhou University of Technology, 2018. (in Chinese)

[17] 杨春山, 莫海鸿, 魏立新. 盾构隧道环向接头等效刚度修正计算及其影响因素研究[J]. 铁道科学与工程学报, 2017, 14(7): 1497-1504.YANG Chunshan, MO Haihong, WEI Lixin. Calculation of Equivalent Stiffness of Shield Tunnel Circumferential Joints and Study of Its Influencing Factors[J]. Journal of Railway Science and Engineering, 2017, 14(7): 1497-1504. (in Chinese)

[18] 邹家兴. 用等效刚度法计算变截面梁的变形[J]. 中国农村水利水电, 1995(9): 36-38. ZOU Jiaxing. Calculation of Deformation of Variable Section Beam by Equivalent Stiffness Method[J]. China Rural Water and Hydropower, 1995(9): 36-38. (in Chinese)

[19] LIU G R, DAI K, NGUYEN T. A Smoothed Finite Element Method for Mechanics Problems[J]. Computational Mechanics, 2007, 39(6): 859-877.

[20] 李军, 吴磊, 孙延超, 等. 某火箭发射系统炮口振动等效刚度分析[J]. 南京理工大学学报, 2013, 37(2): 239-250.LI Jun, WU Lei, SUN Yanchao, et al. Analysis of Muzzle Vibration Equivalent Stiffness of a Rocket Launching System [J]. Journal of Nanjing University of Technology, 2013, 37(2): 239-250. (in Chinese)

[21] 石川千, 周徐斌, 张永涛, 等. 点式连接航天器等效刚度模态分析方法[J]. 航天器工程, 2016, 25(1): 31- 39.SHI Chuanqian, ZHOU Xubin, ZHANG Yongtao, et al. Modal Analysis Method of Equivalent Stiffness of Point Connected Spacecraft [J]. Spacecraft Engineering, 2016, 25(1): 31-39. (in Chinese)

[22] 蔡力钢, 马仕明, 赵永胜, 等. 多约束状态下重载机械式主轴有限元建模及模态分析[J]. 机械工程学报, 2012, 48(3): 165-173.CAI Ligang, MA Shiming, ZHAO Yongsheng, et al. Finite Element Modeling and Modal Analysis of Heavy-duty Mechanical Spindle Under Multiple Constraints[J]. Journal of Mechanical Engineering, 2012, 48(3): 165-173. (in Chinese)

[23] 张云涛. 固定桁架可展开结构的设计与仿真分析[D]. 西安: 西安电子科技大学, 2014.ZHANG Yuntao. Design and Simulation Analysis of Fixed Truss Deployable Structure[D]. Xi'an: Xidian University, 2014. (in Chinese)

[24] 张忠, 张正平, 李海波, 等. 正弦扫频试验振动台与负载界面力获取方法[J]. 振动、测试与诊断, 2017, 37(1): 158-162.ZHANG Zhong, ZHANG Zhengping, LI Haibo, et al. Acquisition Method of Interface Force Between Vibration Table and Load in Sine Sweep Test[J]. Vibration, Test and Diagnosis, 2017, 37(1): 158-162. (in Chinese)

[25] 孙忠涛, 车英. 振动试验台夹具设计及频率响应特性研究[J]. 长春理工大学学报(自然科学版), 2010, 33(2): 61-67.SUN Zhongtao, CHE Ying. Research on the Design and Frequency Response Characteristics of Vibration Test-bed Fixture[J]. Journal of Changchun University of Technology (Natural Science Edition), 2010, 33(2): 61-67. (in Chinese)

[26] 沈凤霞. 正弦振动试验及结构响应数据处理方法[J]. 航天器环境工程, 2004, 21(4): 7-13.SHEN Fengxia. Sine Vibration Test and Structure Response Data Processing Method[J]. Spacecraft Environmental Engineering, 2004, 21(4): 7-13. (in Chinese)

The Simulation Design and Test Research on Scissor Type Hinge Expandable Ring

LIANG Hao WANG Liwu TANG Minzhang ZHU Qian LIU Yuanyuan

（Beijing Institute of Space Mechanics & Electricity，Beijing 100094, China）

With the rapid development of space technology, space equipment is becoming larger and larger. The deployable structure is an effective means to overcome the inner envelope limitation. As a traditional deployable structure, scissor-like element has broad application prospects. But the scissor-like element often has many parts, it needs a lot of time in numerical simulation and it is difficult to iterate quickly. Equivalent stiffness method can greatly reduce the size and complexity of finite element meshed and it is a fast calculation method. In this paper, a circular expandable structure is designed, first-order fundamental frequency is calculated by equivalent stiffness method, the experimental verifications is also carried out. The results show that the equivalent stiffness method can greatly reduce the size and complexity of the finite element mesh, it can realize fast design iteration with accuracy less than 4%.

scissor-like element; equivalent stiffness method; deployable structure; sinusoidal oscillation; lens hood; space camera

V11

A

1009-8518(2020)01-0064-09

10.3969/j.issn.1009-8518.2020.01.008

2019-08-10

梁浩, 王立武, 唐明章, 等. 剪式铰可展开圆环设计、仿真与试验[J]. 航天返回与遥感, 2020, 41(1): 64-72.

LIANG Hao, WANG Liwu, TANG Minzhang, et al. The Simulation Design and Test Research on Scissor Type Hinge Expandable Ring[J]. Spacecraft Recovery & Remote Sensing, 2020, 41(1): 64-72. (in Chinese)

梁浩，男，1989年生，2016年获北京交通大学材料科学与工程专业硕士学位，工程师。研究方向为航天回收结构机构设计。E-mail：351465101@qq.com。

（编辑：王丽霞）