小推力航天器的地球—火星转移轨道混合设计方法

彭坤 曾豪 田林 侯振东

小推力航天器的地球—火星转移轨道混合设计方法

彭坤 曾豪 田林 侯振东

（中国空间技术研究院载人航天总体部，北京 100094）

小推力航天器由于其推进系统的高比冲特性，变轨过程可节省大量推进剂，可用于未来火星探测的地球—火星轨道转移任务中。文章提出一种混合设计方法对小推力航天器的地球到火星的转移轨道优化问题进行求解。根据极大值原理确定小推力发动机的最优控制律，舍弃横截条件，将终端状态量误差和终端质量作为评价指标，采用人工免疫算法对伴随变量和飞行时间进行寻优；混合法、间接法和直接法求解结果表明，混合法比直接法的寻优时间缩短33%，推进剂消耗相当；混合法与间接法在推进剂消耗和状态量方面一致性好，表明混合法的结果接近最优。

地球—火星转移轨道 小推力 混合法 人工免疫算法 火星探测

0 引言

在太阳系内，火星与地球相似度最高且距离较近，是进行载人星际探测的首选目标天体。自20世纪60年代起，人类就开始发射无人探测器对火星进行研究[1]，并开展载人火星航行先期技术研究[2]和后续载人火星探测任务规划[3]，以最终实现载人火星探测和驻留。火星探测任务中的一个关键环节是地球—火星转移轨道设计，若采用高比冲的小推力推进系统则可大幅减少推进剂消耗，从而降低运载火箭的发射质量[4-5]。

小推力航天器的地火转移轨道设计的重点是求解最优控制问题，按照使用极大值原理的程度可分为间接法、直接法及混合法[6-7]。间接法是利用极大值原理，引入哈密顿函数和伴随变量，将最优控制问题转化为两点边值问题，并采用打靶法对伴随变量初值进行求解，通过求解伴随变量从而得到最优小推力转移轨道[8-9]。间接法初值难以估计，收敛半径较小。直接法[10]是利用配点法和模拟函数法等方法对最优控制问题的状态变量和控制变量直接进行离散化，将最优控制问题转化为非线性规划问题，并采用SOCS算法[11]、伪光谱法[12]、SQP方法[13]、遗传算法[14]、人工免疫算法[15]以及Ordinal Optimization方法[16]对非线性规划问题进行求解。直接法对初值不敏感，但计算量随计算精度提高而大幅增加，且不严格保证其求解结果的最优性。混合法[17-18]是将间接法和直接法结合起来，保留间接法的最优控制律，采用多重打靶法[19]和SQP方法[20]对伴随变量初值进行寻优，从而得到最优小推力地火转移轨道。混合法计算量比直接法小，收敛性比间接法好。

本文根据地球和火星的轨道特性建立归一化的二维极坐标动力学模型，由极大值原理确定小推力发动机的最优控制律，将伴随变量和飞行时间作为待优化变量，采用终端质量和终端状态量误差作为评价指标，形成小推力地球—火星转移轨道混合法优化模型，并采用智能优化算法——引导型人工免疫算法（Guiding Artificial Immune Algorithm，GAIA）进行优化求解。并将混合法求解结果与直接法和间接法进行比对，验证混合法求解结果的最优性及其寻优性能。

1 系统模型

地球和火星绕太阳旋转的轨道均为近圆轨道且轨道面相近，可简化为共面圆轨道。在二维极坐标系下描述小推力航天器的地火转移过程，期间忽略地球和火星引力摄动，并以小推力航天器从地球出发时刻的日心距0和质量0作为参考量，建立地球—火星转移轨道的归一化动力学方程[15]（物理量上方横线表示归一化）

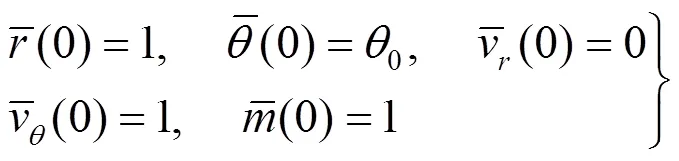
最大则表示推进剂消耗最小，即为最优地球—火星转移轨道。

2 最优控制律

3 混合优化模型

3.1 待优化变量

3.2 状态方程

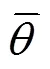
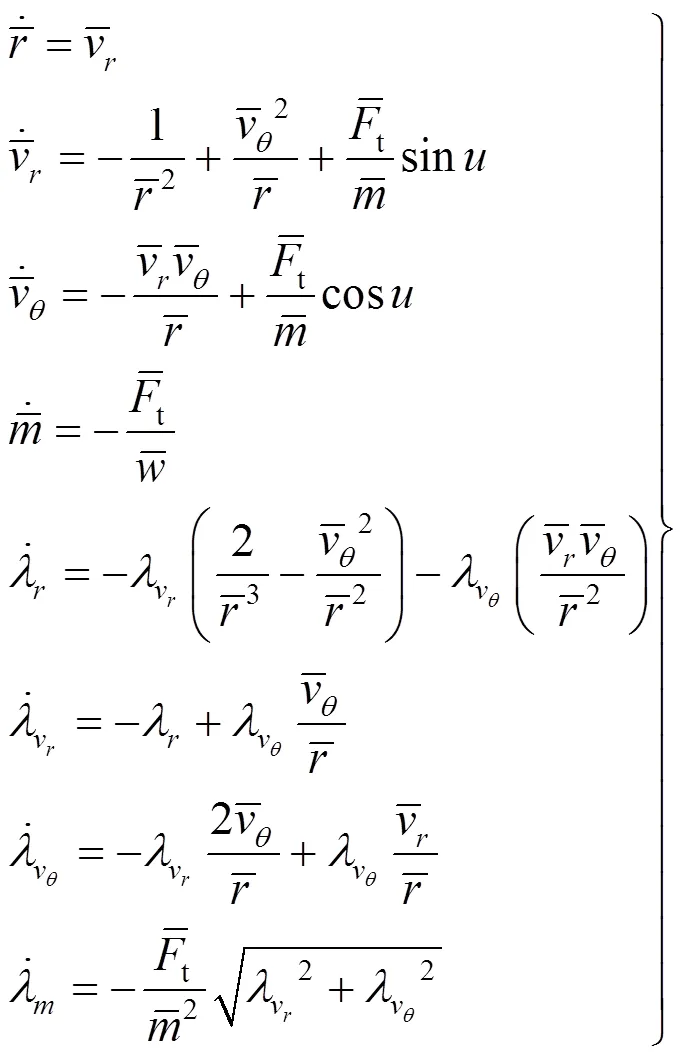
3.3 评价函数

将地球—火星转移轨道的终端约束作为罚函数的形式加入评价指标aff中，如式（10）[15]所示

3.4 优化算法

建立混合优化模型后，需要选取优化算法对其进行求解。由于待优化变量中存在伴随变量初值，仍存在一定敏感性，若采用非线性规划算法则收敛性较差。本文采用智能优化算法——人工免疫算法[15]对优化模型进行求解，增加寻优过程的收敛性。

人工免疫算法是模拟生物免疫系统智能行为而提出的仿生算法，抗体对应待优化变量。其特点是通过激励度计算综合评价抗体亲和度和浓度，并采用种群刷新操作引入新的抗体替换激励度低的抗体，保持抗体多样性，防止陷于局部最优。此外，该算法通过引导型免疫操作快速搜索次优解附近区域，提高局部收敛速度。该算法步骤如下：

1）进行抗原识别，定义亲和度评价函数；2）设置种群中抗体个数，并根据抗体的范围限制随机产生一个初始种群；3）计算抗体的亲和度；4）判断是否满足算法终止条件，如果满足，则终止寻优并输出计算结果，否则继续寻优计算；5）计算抗体的浓度，并进一步计算激励度；6）进行免疫处理，包括免疫选择、克隆、变异和克隆抑制；7）进行种群刷新，并转至第3）步。

4 仿真分析

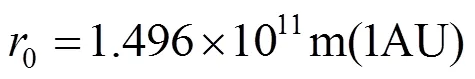
采用GAIA混合法进行10次搜索，9次收敛最优值，1次收敛到最优值附近。将混合法搜索到的最优结果与间接法和GAIA直接法结果[15]进行对比，如表1和图1~图4所示。

表1 间接法、直接法和混合法的寻优结果

Tab.1 Optimization results obtained by indirect, direct and hybrid method

图1为GAIA混合法求得的最优小推力地球—火星转移轨道在日心黄道惯性系中的轨迹示意。轴指向春分点方向，轴指向地球公转轨道角动量方向，轴由右手定则确定。图1中紫色箭头为轨道转移过程中推力方向。由图1可知，小推力航天器先沿着径向正向加速，后沿着径向负向加速，直到航天器到达火星轨道。整个飞行过程耗时215.269天，推进剂消耗为初始质量的31.194%。

将GAIA混合法的归一化结果转化到真实模型，并与GAIA直接法和间接法的结果进行对比。图2为三种方法的状态变量曲线对比。由图2可看出，GAIA混合法求得的4个状态变量曲线与间接法曲线完全重合，证明了其理论最优性。而GAIA直接法的径向速度和横向速度曲线与间接法均有一定偏差，说明其不是理论最优解。图3为三种方法的推力方向角曲线。由图3可知，GAIA混合法由于采用最优控制律，与间接法曲线完全重合；而GAIA直接法由于多项式函数无法完全拟合最优控制律而造成一定偏差，这也造成了其所求解不是理论最优解。

图1 小推力航天器最优地球–火星转移轨道飞行轨迹

图2 间接法、GAIA直接法和GAIA混合法的状态变量变化曲线

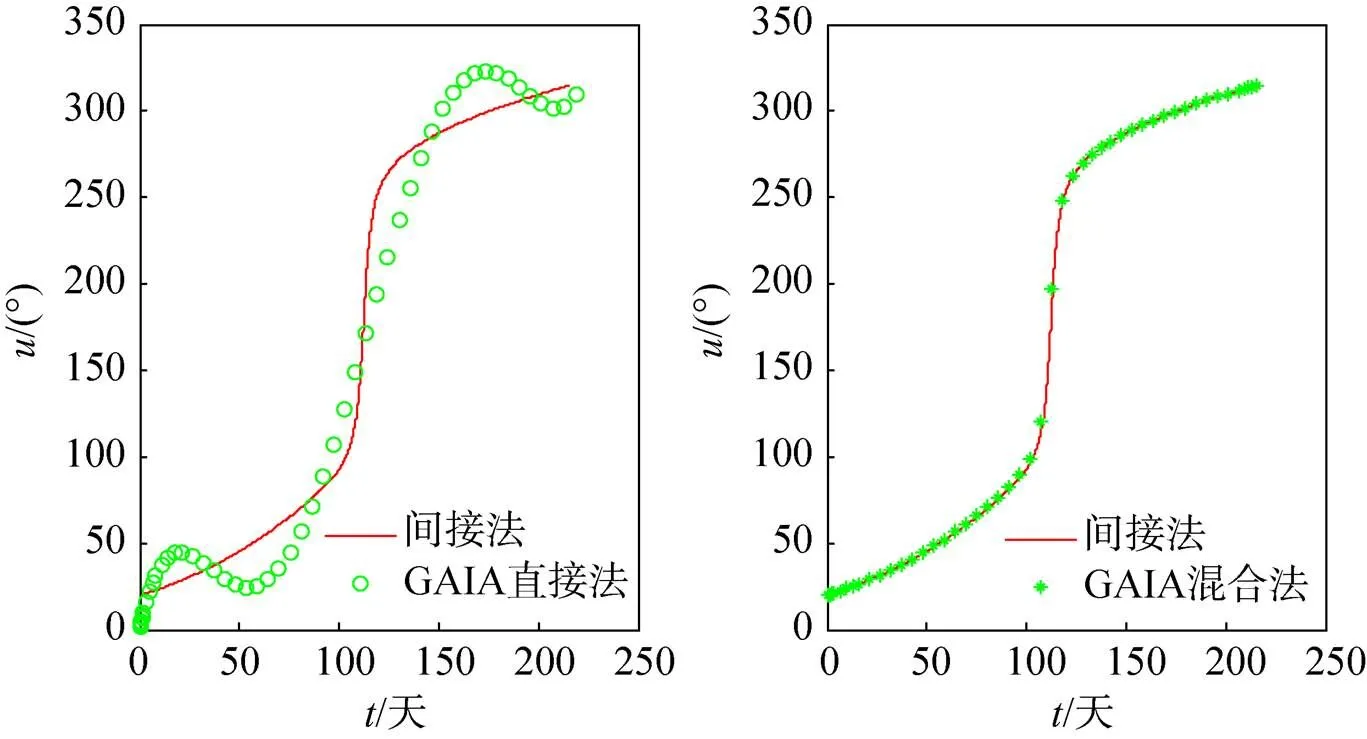
图3 间接法、GAIA直接法和GAIA混合法的推力方向角变化曲线

图4 间接法和GAIA混合法的归一化伴随变量变化曲线

5 结束语

本文针对小推力航天器地球—火星轨道转移过程建立一套混合优化模型，并采用人工免疫算法进行求解，得到了最优小推力地球—火星转移轨道。该混合设计方法比直接法寻优速度快，其单次寻优时间比直接法缩短33%；同时其寻优结果比直接法更优，推进剂消耗比直接法少1.5%。此外，该混合设计方法的状态变量、推力方向角和终端质量与间接法几乎相同，证明了其寻优结果的理论最优性；同时，伴随变量初值不同不影响混合设计方法的寻优正确性，且采用随机优化算法进行优化，有效降低了初值敏感性，收敛性比间接法更好。

[1] 于登云, 孙泽州, 孟林智, 等. 火星探测发展历程与未来展望[J]. 深空探测学报, 2016, 3(2): 108-113. YU Dengyun, SUN Zezhou, MENG Linzhi, et al. The Development Process and Prospects for Mars Exploration[J]. Journal of Deep Space Exploration, 2016, 3(2): 108-113. (in Chinese).

[2] 朱毅麟. 载人火星航行的先期研究[J]. 航天器工程, 2006, 15(2): 1-5. ZHU Yilin. Advance Research on Manned Mars Mission[J]. Spacecraft Engineering, 2006, 15(2): 1-5. (in Chinese).

[3] 李虹琳, 李金钊. NASA发布载人火星探索之路[J]. 中国航天, 2015, 11: 19-20. LI Honglin, LI Jinzhao. NASA Announced the Road of Manned Mars Exploration Mission[J]. Aerospace China, 2015, 11: 19-20. (in Chinese).

[4] LANDAU D F, LONGUSKI J M. Trajectories for Human Missions to Mars, Part 2: Low-thrust Transfers[J]. Journal of Spacecraft and Rockets, 2006, 43(5): 1043-1047.

[5] DERZ U, SEBOLDT W. Mars Sample Return Mission Architectures Utilizing Low Thrust Propulsion[J]. Acta Astronautica, 2012, 77: 83-96.

[6] CHUANG C H, GOODSON T D, LEDSINGER L A. Theory and Computation of Optimal Low- and Medium-thrust Orbit Transfers: NASA-CR-202202[R]. Huntsville, Alabama: Marshall Space Flight Center, 1996.

[7] GAO Y. Advances in Low-thrust Trajectory Optimization and Flight Mechanics[D]. Columbia: University of Missou, 2003.

[8] REDDING D, BREAKWELL J V. Optimal Low-thrust Transfers to Synchronous Orbit[J]. Journal of Guidance, Control, and Dynamics. 1984, 7(2): 148-155.

[9] NAH R S, VADALI S R, BRADEN E. Fuel-optimal Low-thrust Three-dimensional Earth-Mars Trajectories[J]. Journal of Guidance, Control, and Dynamics. 2001, 24(6): 1100-1107.

[10] KLUEVER C A. Optimal Low-thrust Interplanetary Trajectories by Direct Method Techniques[J]. Journal of the Astronautical Sciences, 1997, 45(3): 247-262.

[11] BETTS J T, ERB S O. Optimal Low Thrust Trajectories to the Moon[J]. SIAM Journal of Applied Dynamical Systems. 2003, 2(2): 144-170.

[12] 朱永生. 地球-火星转移轨道设计与优化技术研究[D]. 南京: 南京航空航天大学航天学院, 2013. ZHU Yongsheng. Research on Design and Optimization of Earth-Mars Transfer Orbit[D]. Nanjing: College of Astronautics, Nanjing University of Aeronautics and Astronautics, 2013. (in Chinese).

[13] 尚海滨, 崔平远, 栾恩杰. 地球-火星的燃料最省小推力转移轨道的设计与优化[J]. 宇航学报, 2006, 27(6): 1168-1173. SHANG Haibin, CUI Pingyuan, LUAN Enjie. Design and Optimization of Earth-Mars Optimal-fuel Low-thrust Trajectory[J]. Journal of Astronautics, 2006, 27(6): 1168-1173. (in Chinese).

[14] WALL B, CONWAY B A. Near-optimal Low-thrust Earth-Mars Trajectories via a Genetic Algorithm[J]. Journal of Guidance, Control, and Dynamics. 2005, 28(5): 1027-1031.

[15] 彭坤, 徐世杰, 果琳丽, 等. 基于人工免疫算法的地球-火星小推力转移轨道优化[J]. 中国空间科学技术, 2012, 32(5): 61-68. PENG Kun, XU Shijie, GUO Linli, et al. Optimization of Earth-Mars Low-thrust Trajectory Based on Artificial Immune Algorithm[J]. Chinese Space Science and Technology, 2012, 32(5): 61-68. (in Chinese).

[16] LIU F, LIAO Y, YANG X R. Optimal Design of Earth-Mars Low-thrust Trajectory Transfer Based on Ordinal Optimization Theory [C]//International Conference on Information Engineering and Computer Science, Dec 19-20, 2009, Wuhan, China. IEEE, 2009.

[17] PIERSON B L, KLUEVER C A. Three-stage Approach to Optimal Low-thrust Earth-Moon Trajectories[J]. Journal of Guidance, Control, and Dynamics, 1994, 17(6): 1275-1281.

[18] KLUEVER C A, PIERSON B L. Optimal Low-thrust Three-dimensional Earth-Moon Trajectories[J]. Journal of Guidance, Control, and Dynamics, 1995, 18(4): 830-837.

[19] GAO Y, KLUEVER C A. Low-thrust Interplanetary Orbit Transfers Using Hybrid Trajectory Optimization Method with Multiple Shooting, AIAA 2004-5088[C]//AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Aug 16-19, 2004, Providence, Rhode Island. AIAA, 2004.

[20] 任远, 崔平远, 栾恩杰. 利用混合法进行地球-火星小推力轨道设计[J]. 哈尔滨工业大学学报, 2007, 39(3): 359-362. REN Yuan, CUI Pingyuan, LUAN Enjie. An Earth-Mars Low-thrust Trajectory Design Based on Hybrid Method[J]. Journal of Harbin Institute of Technology, 2007, 39(3): 359-362. (in Chinese).

Hybrid Design Method of Earth-Mars Transfer Trajectory for Low-thrust Spacecraft

PENG Kun ZENG Hao TIAN Lin HOU Zhendong

（Institute of Manned Space System Engineering, China Academy of Space Technology, Beijing 100094, China）

Due to the high specific impulse of the propulsion system, low-thrust spacecraft can save a lot of propellant in orbit maneuvers, which can be used in the Earth-Mars orbit transfer in the future Mars exploration. A hybrid design method is proposed to optimize Earth-Mars transfer trajectory for low-thrust spacecraft in this paper. Optimal control law of low-thrust engine is determined via maximum principle, the transversality condition is abandoned, the terminal state variables errors and terminal mass are chosen as evaluation index, and artificial immune algorithm is applied to optimize the adjoint variables and flight time. The solving results of hybrid method, indirect method and direct method show that the optimization time of the hybrid method is 33% shorter than direct method, and the propellant consumptions of the hybrid method and direct method are almost the same. Furthermore, the propellant consumption and state variables of hybrid method are well consistent with the indirect method, which proves the solving results of hybrid method is very close to the optimal solution.

Earth-Mars transfer trajectory; low-thrust; hybrid method; artificial immune algorithm; Mars exploration

V412.4

A

1009-8518(2020)01-0010-08

10.3969/j.issn.1009-8518.2020.01.002

2019-12-11

载人航天预先研究项目（010201）；中国空间技术研究院杰出青年人才计划

彭坤, 曾豪, 田林, 等. 小推力航天器的地球—火星转移轨道混合设计方法[J]. 航天返回与遥感, 2020, 41(1): 10-17.

PENG Kun, ZENG Hao, TIAN Lin, et al. Hybrid Design Method of Earth-Mars Transfer Trajectory for Low-thrust Spacecraft[J]. Spacecraft Recovery & Remote Sensing, 2020, 41(1): 10-17. (in Chinese)

彭坤，男，1984年生，2010年获北京航空航天大学飞行器设计专业博士学位，高级工程师。研究方向为航天器总体设计、任务规划与轨道设计优化。E-mail：bhkpeng@126.com。

（编辑：王丽霞）