一种新的星载光学遥感器光轴指向运动滤波方法

侯帅 于飞 李超 刘成 黄刚 侯丹 赵丽婷

一种新的星载光学遥感器光轴指向运动滤波方法

侯帅 于飞 李超 刘成 黄刚 侯丹 赵丽婷

（北京空间机电研究所，北京 100094）

针对应用在动中成像的星载光学遥感器光轴指向运动进行准确的运动估计问题，需要在测量出相机光轴的运动信息后对噪声进行滤波，以获得准确的相机光轴指向偏移量。文章对低通滤波、最小均方自适应滤波、卡尔曼滤波和无迹卡尔曼滤波等四种常见方法进行了试验分析，明确了低通滤波方法有更好的效果和适应性，但是性能还需要进一步提升。对相机光轴运动的随机性与所受噪声的统计特征不可预知性，提出了一种根据指向偏移与噪声幅频特性差异自确定截止频率的二次双向低通滤波方法，实现了截止频率的在线估计，解决了常见低通滤波的相位失真问题，滤波效果较四种常见方法更好，满足实际工程应用需求。

动中成像 光轴指向运动 运动估计 运动滤波 光学遥感器 遥感卫星

0 引言

星载动中成像光学遥感器可以按照传统或敏捷机动模式，待卫星平台稳定之后进行稳态成像，也可以按照动中成像模式，通过卫星三轴姿态的持续调整，在机动过程中实现非稳态成像。动中成像模式节省了卫星指向姿态调整所占用的时间，并且实现了非沿迹（不沿着飞行轨迹）成像，可对国境线、岛链等非规则曲线进行异轨观测[1]。

在动中成像遥感观测中，需要获得精确的成像系统光学指向偏移量来实现抖动后模糊图像的复原或者TDI焦面的行转移积分时间的实时准确设置。为准确地获得动中成像过程中相机光轴运动信息，可以通过高帧频图像的成像匹配方法来实现[2-4]。然而，在使用高帧频相机对相机光轴运动的观测过程中，由于相机对卫星平台振动的响应和图像匹配算法的误差等其他影响测量精度的因素，测量出的相机光轴运动信息会带有噪声。为获得高精度的相机光轴运动信息，必须要利用运动滤波算法消除或减小噪声。

1 光轴运动模型与传统滤波方法

1.1 光轴运动分析与建模

卫星平台指向指令输出的运动是一个平滑的曲线。然而在成像过程中，由于卫星姿态的持续调整，如动量轮变速转动、喷气等工作引起的平台振动和卫星的指向控制，如太阳翼、指向反光镜、天线、飞轮等运动部件调整引起的整星振动，会产生震颤。对于高分辨率相机而言，这种震颤的频率较低，幅值较大，是造成相机光轴指向偏移的主要因素，导致相机光轴的运动会与卫星平台指向指令运动存在误差，是影响成像品质的主要原因。通过高帧频图像的成像匹配来观测相机光轴运动的过程中，由于相机对卫星平台振动响应的高频成分导致的相机亚像元模糊以及图像匹配算法的误差等其他影响测量精度的因素，会产生噪声。对于成像系统而言，这种噪声的频率较高，幅值较小[5]，一般为卫星姿态控制精度的千分之一以下。图1为平台指向指令运动曲线和成像过程中与观测到的相机光轴垂直方向的整体和局部放大运动曲线，其中灰色曲线为平台指向指令运动曲线，蓝色曲线是相机在成像过程中由于受到频率较低、幅值较大的震颤影响造成光轴指向随机偏移的实际运动曲线，红色曲线是通过高帧频相机观测相机光轴运动得到的带有频率较高、幅值较小的随机噪声的相机光轴运动曲线。

1.2 常见滤波方法试验与结果分析

为提高对相机光轴运动观测的精度，要消除或减小噪声。由于噪声的能量较低，难以在部件正常工作的限制下进行控制，主动地消除噪声。因此，只有被动地选用滤波的方法来消除或者减小噪声。常见的滤波方法有：低通滤波[6-8]、最小均方（LMS）自适应滤波[9-12]、卡尔曼滤波[13-16]和无迹卡尔曼滤波[17-19]。

使用这四种常见方法对观测到的相机光轴运动曲线进行1 000次随机实时滤波试验，共计123 000个采样点，本次滤波选取1 000个采样点，具体设置如下：

1）随机指向偏移频率范围0.1~100Hz，随机噪声频率范围50~1 000Hz；

2）低通滤波截止频率选取为指向偏移最高频率100Hz，通过峰值匹配方法矫正相位；

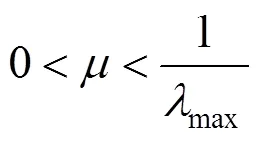
4）卡尔曼滤波和无迹卡尔曼滤波中，设定状态方程为平台垂直方向指向指令运动曲线加上随机指向偏移，即成像过程中相机光轴实际运动曲线，观测方程为在此基础上加上随机噪声，即观测到的相机光轴运动曲线；

对比滤波前后的相机光轴运动曲线如图2所示。计算并记录噪声均方根（RMS）值降低的百分比如表1所示。

图1 平台指向指令运动曲线和成像过程中与观测到的相机光轴垂直方向运动曲线

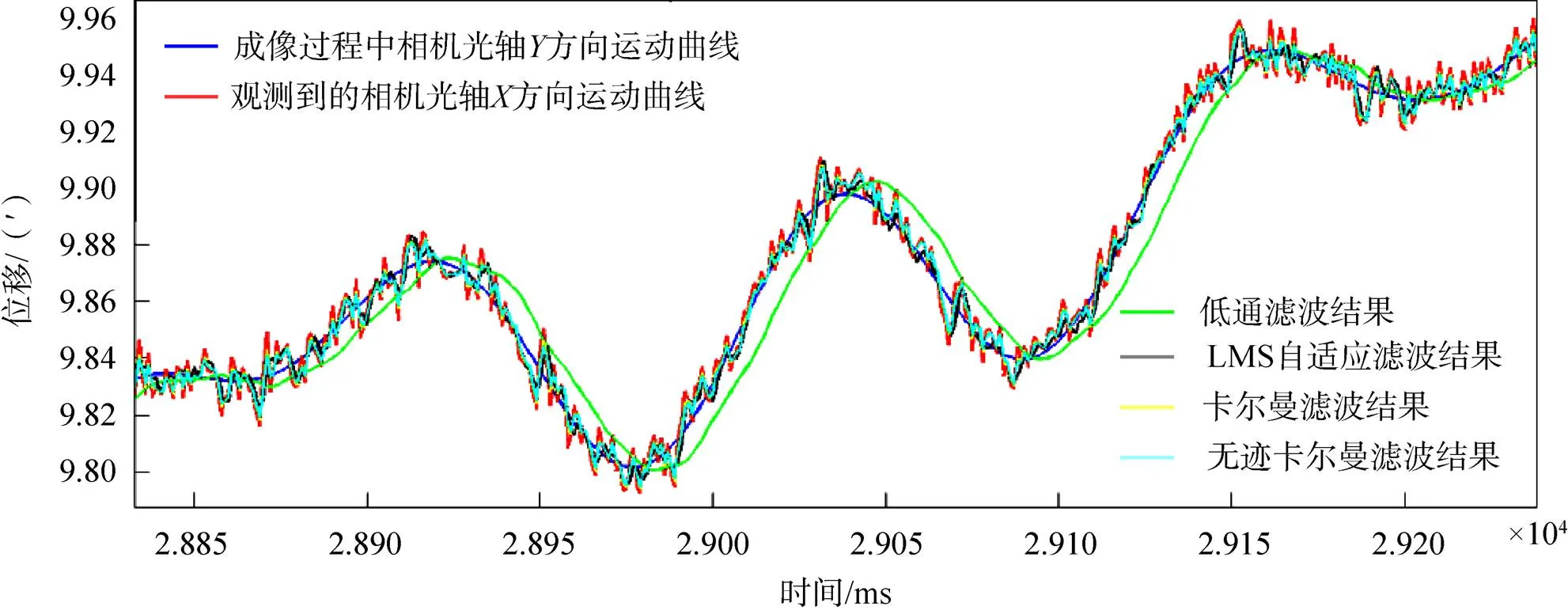
图2 不同方法相机光轴运动滤波结果曲线对比

表1 不同方法滤波结果数据对比

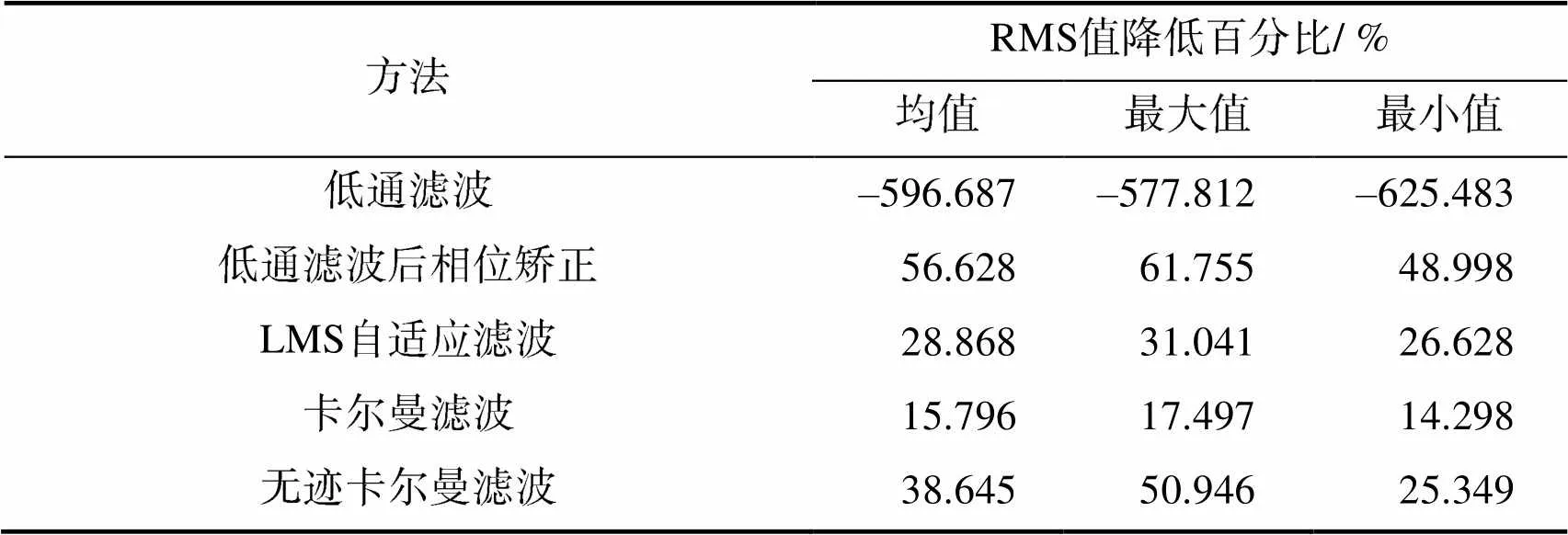
Tab.1 The data comparison of the results in different methods

从上述试验结果可以看出：

1）经过低通滤波后的相机光轴运动曲线变得较为平滑，噪声被较好地抑制，但是发生了较为严重的相位失真。由于相位失真的原因，导致滤波后的噪声RMS值升高；经过相位矫正后，噪声RMS值有所降低。

2）经过LMS自适应滤波后的相机光轴曲线较不平滑，噪声RMS值降低程度较小。

3）经过卡尔曼滤波和无迹卡尔曼滤波后的相机光轴曲线较不平滑，噪声的RMS值有较小幅度的降低。

所以，上述四种常见滤波方法对相机光轴运动曲线的滤波效果均不理想，分析如下：

对于低通滤波方法，首先，由于无限脉冲响应滤波的系统函数中存在着不为零的极点，导致输出只可能实现与输入近似的线性相位特性，存在着相位偏移；其次，在实际情况下，由于极点的变化，很难实现对输出的精确相位矫正；最后，截止频率的选取依赖于对噪声产生源的预先分析与频率估计，会与实际情况下的噪声频率存在偏差，使得滤波效果降低。

对于LMS自适应滤波方法，首先，期望输出应为成像过程中相机光轴运动曲线，在实际情况下这是未知量也是需求；其次，期望输出的平坦程度决定了滤波算法的收敛速度与收敛性，而成像过程中相机光轴运动曲线并不平坦，会导致滤波算法的收敛速度较慢甚至不收敛；最后，收敛因子的选取在实际应用中难以确定最优值，难以保证滤波过程的稳定性。

对于卡尔曼滤波和无迹卡尔曼滤波方法，首先，由于动中成像相机光轴的实际运动较为复杂，具有随机性且随机状态不确定，在这种情况下，会导致协方差预测与滤波增益计算的不准确甚至失效；其次，由于指向偏移和噪声的随机性，他们的统计特性不可提前预知，同样导致了协方差预测与滤波增益的计算不准确；最后，卡尔曼系滤波方法要求噪声为高斯分布的白噪声，而相机光轴运动的指向偏移和噪声均不满足这一限制条件。

从上述的分析可以看出，LMS自适应滤波和卡尔曼系滤波方法的限制条件严重影响了对相机光轴运动滤波的效果，而低通滤波方法基本上没有条件上的限制，只需解决相位失真和截止频率估计的问题，便可以获得较为理想的滤波效果，是一种值得改进的方法。

2 低通滤波方法的改进

2.1 截止频率的确定

常见低通滤波方法的截止频率选取一般是通过前期对于噪声声源的了解分析与试验测试，得到的噪声频率范围从而确定截止频率。而对星载动中成像光学遥感器来说，噪声声源与航天环境均较为复杂，估计到的截止频率会与实际情况存在偏差，导致滤波效果受限。可行的方法是在线测量与分析噪声频谱，使用某种方法辨别噪声与有用信息的频率差异，从而确定截止频率。

将观测到的相机光轴运动与理想情况下的相机光轴运动进行比较可以得到指向偏移和噪声的混合信息，其频谱如图3所示。

图3中可以看到，在低频部分分布的主要为需要保留的指向偏移信息，幅值相对较大；在高频部分主要分布着需要滤除的噪声，幅值相对较小，两者存在着较为明显的幅值差异。根据幅值的差异可以确定截止频率选取的范围。对混合信息频谱进行均值滤波，滤波窗口大小为系统采样频率大小的一半，得到的结果如图4所示。

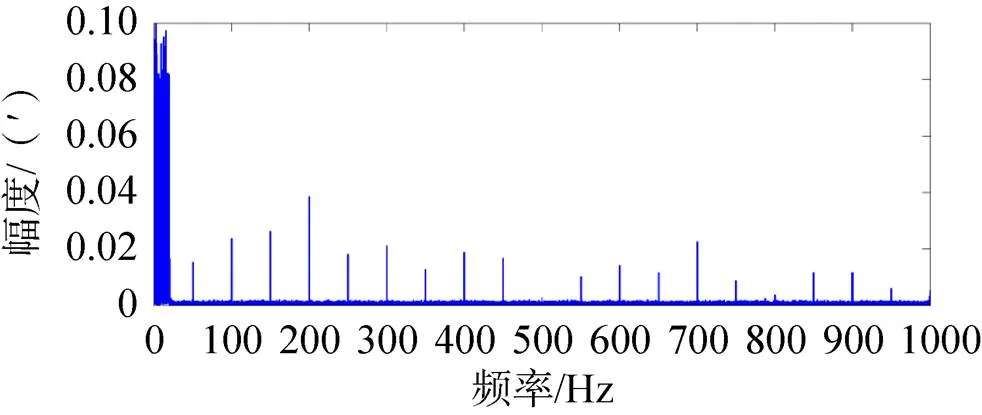
图3 混合信息频谱图

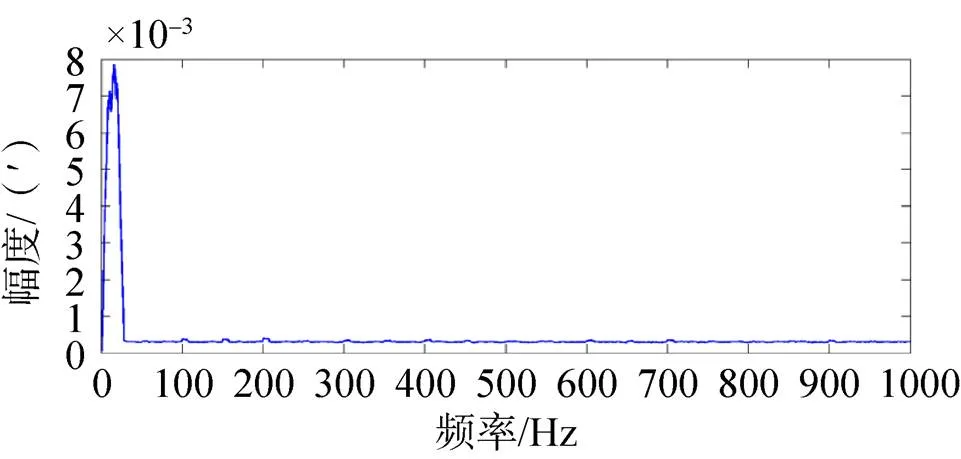
图4 均值滤波后的混合信息频谱图

测量经过均值滤波后的混合信息最大幅值，并计算最大幅值的二分之一处对应的频率，选取其中较大的一个作为截止频率，记录截止频率与指向偏移和噪声的频率范围如表2所示，并进行比较分析。

表2 频率范围与截止频率

Tab.2 The frequency range and the cut-off frequency 单位：Hz

可以看出，指向偏移和噪声的频率范围在相距较近、混叠和相距较远三种不同类型下，该方法确定的截止频率均为合理，完全保留指向偏移信息的同时对观测噪声有着较好地抑制。

2.2 消除相位失真

常见的低通滤波方法的输出会与输入存在非线性的相位偏差，这是由于无限脉冲响应滤波器，其单位脉冲响应是无限长的，其系统的差分方程可以写为[20]

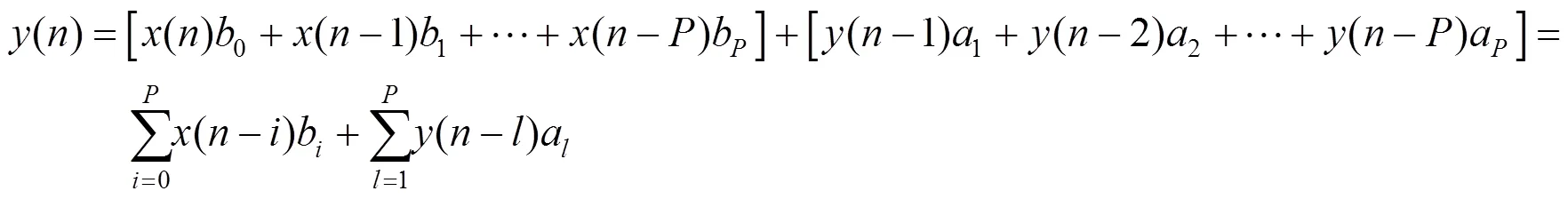
式中()为滤波器输出序列；()为滤波器输入序列；为序列号；为滤波器阶数；a，b为滤波系数，，为差分阶数。

经过变换可以得到

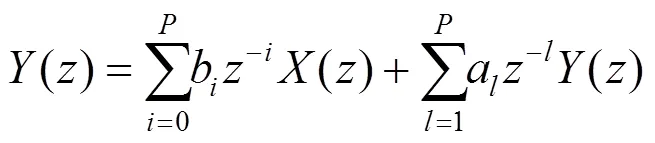
则滤波器的系统函数()为

可以看出，无限脉冲响应滤波器的系统函数()存在着不为零的极点，因此输出只可能实现近似的线性相位特性，会与输入的相位发生偏移。在实际应用过程中，使用峰值匹配方法对相位进行矫正，或用其他方法对输出相位进行测量与调整不仅耗费额外时间，还会引入新的误差，因此应设计一种没有相位失真的低通滤波方法。

双向低通滤波的过程是先将输入按照顺序进行低通滤波，然后将所得的结果时域翻转后再次进行低通滤波，将所得的结果逆再次时域翻转后输出，得到的结果便是无相位失真的低通滤波结果，原理推证如下：

(1) 时域翻转

设输入序列()长度为，经过变换得到

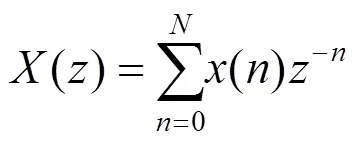
将()进行时域翻转得到()，则()的变换为

（5）

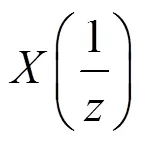
（2）双向低通滤波

根据上述输入序列()进行时域翻转前后的变换关系，双向低通滤波过程可以表述如下：

第一步，将输入()顺序经过低通滤波器()，得到()，即

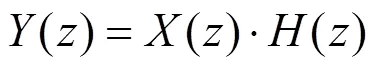
第二步，将()进行时域翻转，得到()，由式（5）、（6）得

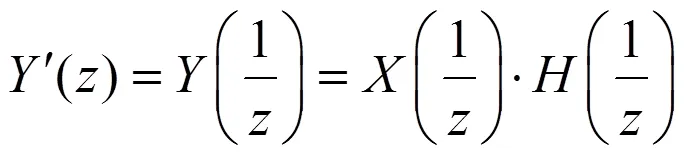
第三步，将()再次通过低通滤波器()，得到()，即

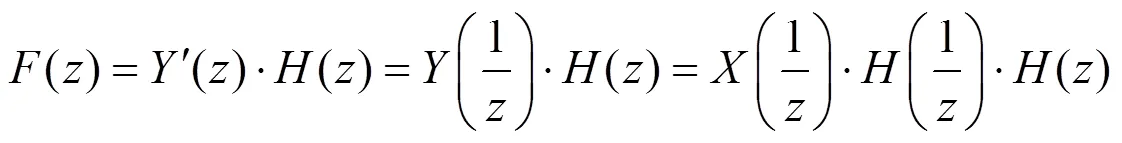
第四步，将()再次进行时域翻转，得到最终输出()，由式（5）、（8）得

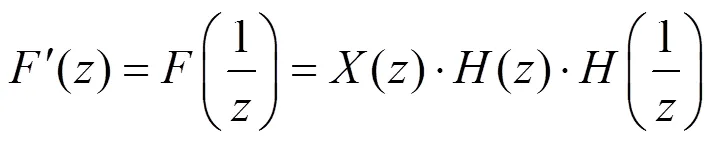
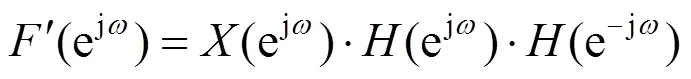
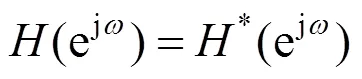
可以看出，经过双向低通滤波的最终输出与输入只是在幅度上的改变，而与输入的相位没有发生变化。

对观测到的相机光轴运动曲线进行自确定截止频率双向低通滤波试验，对比滤波前后的相机光轴运动曲线如图5所示。

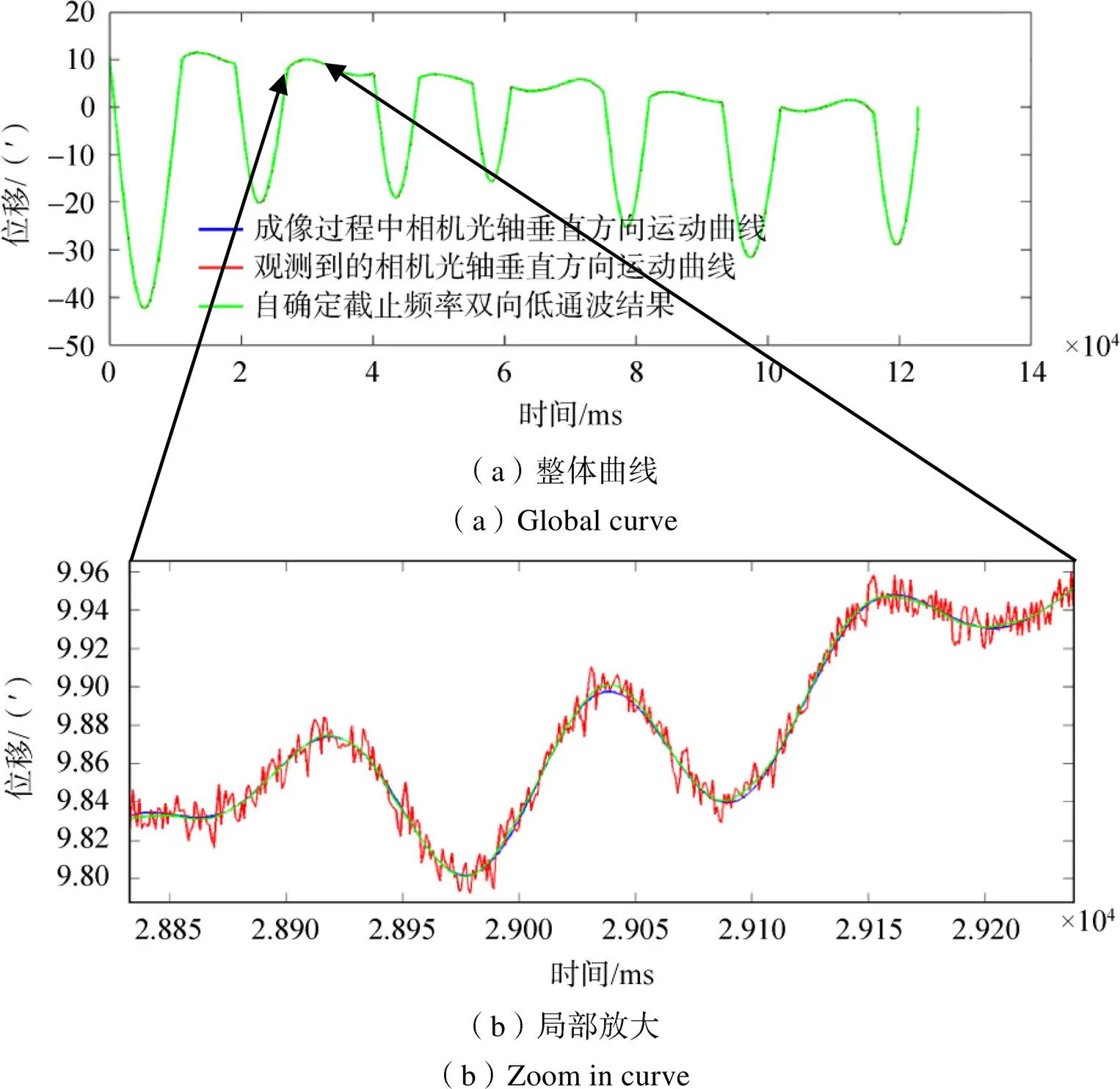
图5 双向低通滤波后的相机光轴运动曲线

可以看出，滤波后的相机光轴运动曲线没有发生相位失真，证明了双向低通滤波方法可以解决传统低通滤波相位失真的问题。

3 试验结果对比与结论

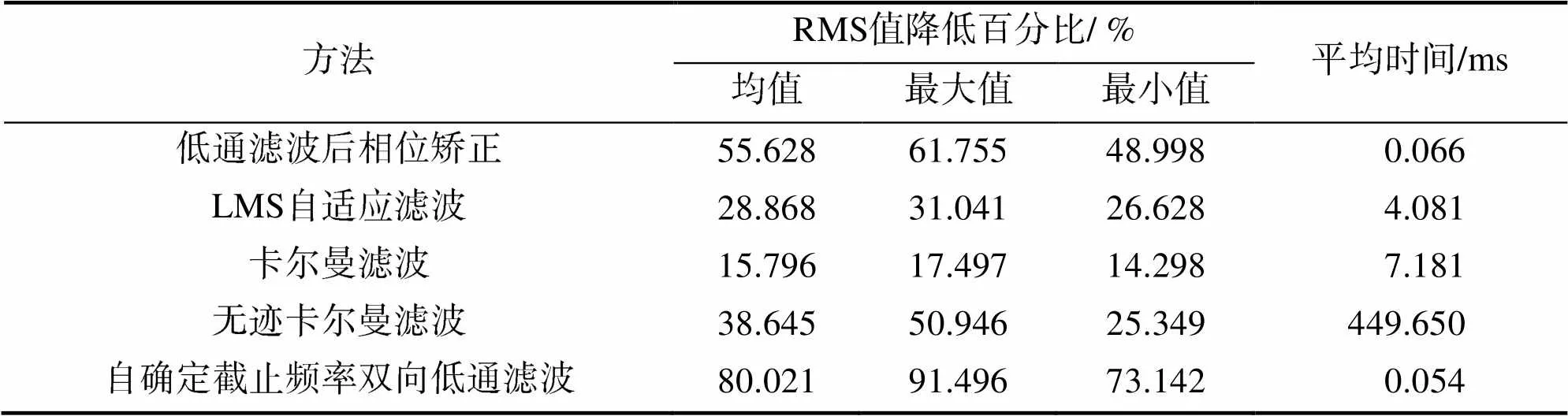
使用低通滤波、LMS自适应滤波、卡尔曼滤波、无迹卡尔曼滤波和自确定截止频率双向低通滤波方法对观测到的相机光轴运动曲线，使用与1.2节中相同的试验进行1 000次滤波试验，计算噪声RMS值降低的百分比，如表3所示。

可以看出，自确定截止频率双向低通滤波方法对于相机光轴运动滤波的效果优于四种常见方法。在1000次随机试验中，该方法对于噪声RMS值降低程度平均达到了80%，最大达到了91%。可见自确定截止频率双向低通滤波方法有良好的滤波效果。同时，在计算时间上，该方法具有较强的实时性，能够满足后续工程应用需求。

表3 不同方法滤波结果数据对比

Tab.3 The data comparison of the results in different filtering methods

4 结束语

本文根据对星载动中成像光学遥感器光轴运动特性与测量过程中所受噪声特性进行分析，使用四种常见方法进行试验，结果表明这四种方法对该问题的滤波效果均不理想，为此，针对低通滤波方法的截止频率确定与相位失真问题，提出了自确定截止频率双向低通滤波方法，试验结果表明该方法获得了较好的滤波效果，具有较好的实用性。

[1] 吴俊, 李娜, 许云飞, 等. 超敏捷卫星动中成像模式下成像质量研究[J]. 光学与光电技术, 2018, 16(5): 83-89. WU Jun, LI Na, XU Yunfei, et al. Research on Imaging Quality of Super Agile Satellite with Dynamic Imaging Mode[J]. Optics & Optoelectronic Technology, 2018, 16(5): 83-89. (in Chinese)

[2] 李超, 于飞, 康晓军. 一种模板匹配的快速实现方法[J]. 航天返回与遥感, 2016, 37(1): 63-70. LI Chao, YU Fei, KANG Xiaojun. A Fast Method of Template Matching[J]. Spacecraft Recovery & Remote Sensing, 2016, 37(1): 63-70. (in Chinese)

[3] 王恺, 陈世平, 曾湧. 一种频域亚像元影像匹配方法[J]. 航天返回与遥感, 2015, 36(1): 81-86. WANG Kai, CHEN Shiping, ZENG Yong. A Subpixel Matching in Frequnecy Domain[J]. Spacecraft Recovery & Remote Sensing, 2015, 36(1): 81-86. (in Chinese)

[4] 蔡晓东, 叶培建. 卫星遥感图像信息作为姿态敏感器的应用研究[J]. 中国空间科学技术, 2005, 25(6): 8-13. CAI Xiaodong, YE Peijian. Research on Satellite Attitude Sensor Applying Remote Sensing Image Information [J]. Chinese Space Science and Technology, 2005, 25(6): 8-13. (in Chinses)

[5] 王密. 高分辨率光学卫星遥感影像平台震颤分析与精确处理方法[M]. 北京: 科学出版社, 2018: 10-11. WANG Mi. High Resolution Optical Satellite Remote Sensing Image Platform Fremitus Analysis and Precision Treatment Method[M]. Beijing: Science Press, 2018: 10-11. (in Chinese)

[6] 郎骏健, 梁星辉, 柳林涛, 等. 航空重力傅里叶基追踪低通滤波方法研究[J]. 地球物理学报, 2018, 61(12): 4737-4745. LANG Junjian, LIANG Xinghui, LIU Lintao, et al. Research on the Fourier Basis Pursuit Low Pass Filter Airbone Gravity[J]. Chinese Journal of Geophysics, 2018, 61(12): 4737-4745. (in Chinese)

[7] 张召磊, 孙晓伟, 夏德新, 等. 高精度频率分辨在振动信号辨识中的应用[J]. 火箭推进, 2017, 43(2): 66-71. ZHANG Zhaolei, SUN Xiaowei, XIA Dexin, et al. Application of High-precision Frequency Resolution in Vibration Signal Identification[J]. Journal of Rocket Propulsion, 2017, 43(2): 66-71. (in Chinese)

[8] 刘云鹏, 马国明, 刘肇鸥, 等. 低通滤波在紫外成像降噪处理中的应用[J]. 高压电技术, 2007, 33(6): 129-113. LIU Yunpeng, MA Guoming, LIU Zhaoqing, et al. Application of Low Pass Filter Technology in Electric Equipment UV Detection[J]. High Voltage Engineering, 2007, 33(6): 129-113. (in Chinese)

[9] 陈琳, 李建勋, 戴虎, 等. 自适应滤波在动态推力测量中的应用[J]. 宇航学报, 2010, 31(7): 1819-1824. CHEN Lin, LI Jianxun, DAI Hu, et al. Application of Adaptive Filter in Dynamic Thrust Measurement[J]. Journal of Astronautics, 2010, 31(7): 1819-1824. (in Chinese)

[10] 王洁, 熊智, 邢丽, 等. 基于新息自适应滤波的惯性测量单元误差在线标定方法研究[J]. 兵工学报, 2016, 37(7): 1203-1213. WANG Jie, XIONG Zhi, XING Li, et al. Online Calibration of IMU Errors of Inertial Navigation System Based on Innovation-based Adaptive Filtering[J]. Acta Armamentarii, 2016, 37(7): 1203-1213. (in Chinese)

[11] 王晓亮, 邵晓巍, 龚德仁, 等. 改进的量测噪声自适应滤波在空间非合作目标视觉导航中的应用[J]. 航天控制, 2011, 29(2): 37-41. WANG Xiaoliang, SHAO Xiaowei, GONG Deren, et al. Application of an Improved Measurement Noise Adaptive Filter in Vision Navigation for Non-cooperative Target in Space[J]. Aerospace Control, 2011, 29(2): 37-41. (in Chinese)

[12] 仇立成, 祝程程. 自适应滤波在GPS测速中的应用[J]. 全球定位系统, 2013, 38(1): 15-17. QIU Licheng, ZHU Chengcheng. The Application of Adaptive Filter in Velocity Measurement with GPS[J]. GNSS World of China, 2013, 38(1): 15-17. (in Chinese)

[13] 王向华, 覃征, 杨新宇, 等. 基于两次Kalman滤波的观测噪声自适应调整算法[J]. 系统工程与电子技术, 2010, 32(2): 232-234. WANG Xianghua, QIN Zheng, YANG Xinyu, et al. Adaptive Algorithm for Adajusting Observation Noises Based on Double-Kalman Filter[J]. Systems Engineering and Elcronics, 2010, 32(2): 232-234. (in Chinese)

[14] 黄磊. 光纤陀螺随机噪声的建模与滤波[J]. 弹箭与制导学报, 2013, 33(6): 27-30. HUANG Lei. Modeling and Filtering Methods of FOG Random Noise[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2013, 33(6): 27-30. (in Chinese)

[15] 张文博, 范大鹏, 张智永, 等. 光电稳定跟踪装置中微机电陀螺应用研究[J]. 光学精密工程, 2006, 14(4): 689-696. ZHANG Wenbo, FAN Dapeng, ZHANG Zhiyong, et al. Research on Application of MEMS Gyro to Servo System for E-O Stabilization and Tracking Devices[J]. Optics and Precision Engineering, 2006, 14(4): 689-696. (in Chinese)

[16] 刘少轩, 马琰, 吴旭光, 等. 稳定跟踪平台陀螺噪声及滤波去噪方法[J]. 工业仪表与自动化装置, 2013(3): 62-66. LIU Shaoxuan, MA Yan, WU Xuguang, et al. Research on Gyro Noise and Filtering of Stabilization and Tracking Platform[J]. Industrial Instrumentation and Automation, 2013 (3): 62-66. (in Chinese)

[17] 刘光明, 徐帆江. 抗差自适应UKF算法在地基光学跟踪空间目标中的应用[J]. 系统工程与电子技术, 2018, 40(3): 623-629. LIU Guangming, XU Fanjiang. Application of Robustly Adptive UKF Algorithm in Ground-based Bearings-only Tracking for Space Targets[J]. Systems Engineering and Elctronics, 2018, 40(3): 623-629. (in Chinese)

[18] 袁丹丹, 易文俊, 管军, 等. 基于UKF弹体滚转姿态测量方法研究[J]. 弹道学报, 2017, 29(2): 8-12. YUAN Dandan, YI Wenjun, GUAN Jun, et al. Study of Projectile Roll-attitude Measurement Method Based on Unscented Kalman Filter[J]. Journal of Ballistics, 2017, 29(2): 8-12. (in Chinese)

[19] 姜雪原, 马广富, 胡庆雷. 改进型UKF滤波算法的卫星姿态估计[J]. 哈尔滨工程大学学报, 2005, 26(4): 544-549. JIANG Xueyuan, MA Guangfu, HU Qinglei. Modified Unscented Kalman Filter for Satellite Attitude Estimation[J]. Journal of Harbin Engineering University, 2005, 26(4): 544-549. (in Chinese)

[20] 杜勇. 数字滤波器的MATLAB与FPGA实现：Xilinx/VHDL版[M]. 北京: 电子工业出版社, 2017: 166. DU Yong. The Implementation of Digital Filter on MATLAB and FPGA: Version of Xilinx/VHDL[M]. Beijing: Publishing House of Electronics Industry, 2017: 166. (in Chinese)

A New Filter Method for Optic Axis Pointing Motion of Spaceborne Optical Remote Sensors

HOU Shuai YU Fei LI Chao LIU Cheng HUANG Gang HOU Dan ZHAO Liting

（Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China）

Aiming at the problem of accurate estimation of the optical axis pointing motion of spaceborne optical remote sensors imaging in motion state, it’s necessary to filter the noise from the measurement information to obtain accurate pointing offset of the optical axis. Four common methods, i.e. low-pass filter, least mean square (LMS) filter, Kalman filter and unscented Kalman filter, are analyzed, and the results show that the low-pass filter method is better in efficiency and adaption, and has potential in improving performance. Considering the randomness of camera optical axis motion and the unpredictability of statistical characteristics of the received noise, a two-way low-pass filter method with self-determined cut-off frequency is proposed according to the difference of amplitude frequency characteristics between the camera optical axis pointing offset and the noise.The experimental results show that this method realizes on-line estimation of cut-off frequency and solves the problem of phase distortion in low-pass filter method, with filtering effect better than the traditional four methods, meeting the needs of practical engineering application.

imaging in motion state; optical axis pointing motion; motion estimation; motion filtering; optical remote sensor; remote sensing satellite

TP79

A

1009-8518(2020)01-0047-09

10.3969/j.issn.1009-8518.2020.01.006

2019-11-20

国家重大科技专项工程

侯帅, 于飞, 李超, 等. 一种新的星载光学遥感器光轴指向运动滤波方法[J]. 航天返回与遥感, 2020, 41(1): 47-55.

HOU Shuai, YU Fei, LI Chao, et al. A New Filter Method for Optic Axis Pointing Motion of Spaceborne Optical Remote Sensors[J]. Spacecraft Recovery & Remote Sensing, 2020, 41(1): 47-55. (in Chinese)

侯帅，男，1995年生，2017年获哈尔滨工程大学学士学位，现在中国空间技术研究院光学工程专业攻读硕士学位。研究方向为精密光电仪器控制。E-mail：137166379@qq.com。

（编辑：王丽霞）