基于混合全局池化的回环检测算法
宋周锐
(北京邮电大学可信分布式计算与服务教育部重点实验室,北京 100876)
0 引 言
移动机器人需要较高的定位精度和效率,它是机器人正确执行其他复杂任务的基础。在全局定位系统(如GPS、北斗等)不能正常工作的场景中(如隧道、室内和其他复杂环境),机器人定位的误差会随时间积累而增大。回环检测技术是指使得机器人识别二次经过某个地点的技术,它可以在一定程度上解决累积误差问题,是移动机器人可靠工作的重要保障。回环检测通过将第二次经过时的位姿与第一次经过时的位姿联合起来,对移动机器人的全局位姿增添新的约束,达到优化全局轨迹的目标,从而消除累积误差,图1展示了回环检测前后累计误差的对比,可以看出经过回环检测以后轨迹更加准确。

图1 回环检测校正全局地图
传统的回环检测算法依赖于人工设计的特征点描述子,采用类似于文本检索的方法将图片中的特征点描述子编码为图片特征向量。然而,人工设计的特征往往只能提取角点、线段等低级特征,不具备高级语义信息,在弱纹理、重复纹理场景中表现较差。近年来,深度学习技术在计算机视觉的多个领域中都取得了令人瞩目的成就,将深度学习应用于回环检测成为机器人领域的研究热点之一。基于深度学习框架的回环检测算法能够提取高级语义特征,相比于传统算法更加鲁棒,而且能够更方便地针对机器人运行环境做出改进。
然而,由于移动机器人能提供的计算资源相对有限,难以支撑大型卷积神经网络实时运行,基于深度学习的回环检测一般都采用较浅的卷积神经网络。显然,小型卷积神经网络难以应用到大型场景中,当机器人运动范围较大时,小型网络提取出的描述子可能不具备足够的区分度。
基于图片相似度的回环检测本质是一种基于图像内容的图片检索问题,因此可以借鉴图像检索的方法和评价标准来设计回环检测算法并对其进行评价。本文选取了图像检索中常用的评价标准衡量算法性能。两者的不同之处在于图像检索任务一般运行在服务器集群上,因此它可以采用大型卷积神经网络在超大规模的图像集中取得很高的精度。如果可以把在大规模数据集上训练好的图像检索模型部署到移动机器人上,显然可以取得非常好的成绩。可不可以将图像检索的模型部署到移动机器人上呢?
文献[1]在图像检索任务上取得了世界领先的精度,其中关键算法是GeM(Generalized Mean),但是GeM引入了复杂的非整数幂运算,不利于移动机器人平台部署。在文献[1]的基础上,本文提出一种解决方案,即混合全局池化层来近似GeM,去除GeM中复杂的非整数幂运算,简化运算复杂度,并达到与之相当的精度;同时,本文还提出一种基于块浮点数的卷积神经网络加速引擎,可以将卷积层中浮点数运算替换为定点数运算。与32位浮点算法相比,采用块浮点算法可将加法运算的硬件能耗减少80%以上,乘法运算能耗减少20%。通过这2点改进,可以将图像检索算法部署到移动机器人上。
1 相关工作
1.1 基于深度学习的图像特征提取相关工作
人为设计的特征点描述算法往往对光照变化较为敏感[2],因此学者们开始探索通过卷积神经网络(CNN)来学习图像描述子的方法[3-5]。文献[6]将CNN运算过程中各卷积层的输出结果作为图片描述子,它将图片输入已经训练好的CNN模型中,把CNN计算过程中各层的中间结果取出来,发现越深的层结果就越抽象。这种高度抽象的能力使得利用CNN提取图片中的语义信息并保持高度的稳定性成为可能。
文献[7]采用了一种基于自编码网络的方法,它将原始图片输入到SDA(Stacked Denoising Auto-encoder)中,编码网络会学习一种对图片的压缩编码方式,并根据解码网络解码所得结果与原图片的差异来调整编解码网络参数。本文使用自编码网络输出的压缩编码作为图片描述子,并在多个数据集上取得了state-of-art的效果。但是由于SDA的训练与测试使用的是相同的数据集,缺乏对SDA的泛化能力的实验论证。文献[8]提出了一种轻量的回环检测框架,它通过对图片进行裁剪、旋转构造训练集训练了一个较浅的卷积神经网络用于回环检测,它结构简单、计算复杂度低,对移动机器人等计算资源受限平台友好,但是它在大型数据集上表现不够好,难以应对移动机器人长时间运行的场景。
文献[9]将孪生网络(siamese convolutional neural network)应用于回环检测任务,提出了一种端到端(end-to-end)的解决方案。通过将图片对输入到孪生网络中,调整网络参数使得回环的图片对在距离空间中更近。该方法使用了图片对在网络各层的输出结果作为特征,形成层级化的图片描述子,达到了既能利用低级特征也能利用高级特征的目标。同时,通过对这些特征进行加权处理使之保持在256维,降低了后续匹配的计算代价,整个模块能以较快的速度运行。但是也正因为该网络较浅,缺乏表达复杂多样环境的能力,在大型场景中表现不够理想。
1.2 卷积神经网络加速相关工作
深度学习模型压缩和剪枝技术主要用来降低深度学习模型的带宽需求并缩小其存储规模。压缩和剪枝法的理论基础是卷积神经网络本身所带有的冗余性,这2项技术通常结合使用。文献[10]提出了一种在168个处理元素上的数据流存储方式,通过只复用局部数据,达到了提升功率效率的目标。文献[11]提出了一种屋顶模型(roofline model)来分析一个具体的CNN模型的计算和内存需求曲线,从而确定在指定FPGA或者专用芯片平台上的最优部署方法。另一种流行的思路是稀疏化CNN模型的参数。文献[12-13]提出了一种3段式的压缩方法,这3段分别是剪枝、量化参数再训练、对量化后的参数进行哈夫曼编码(Huffman coding)。通过这3段处理,显著地压缩了DNN的大小,并几乎没有精度损耗。然而该方法的问题在于重新训练稀疏模型是非常耗时的,而且每次调整神经网络架构都需要重复这一过程。同时,在导入FPGA之后,进行计算时依然使用的是浮点数运算。使用哈夫曼编码在缩小了模型体积的同时也带来了解码的开销,这就导致了模型加载时的额外开销。文献[14]使用的剪枝技术同样有需要重新训练的弊端,因为剪枝技术的本质在于通过反复尝试找到关键连接并摒弃非关键连接,达到减少连接数目的目标。
与上述思路不同的是,替换数值表示形式[15-18]这种方法的主要出发点是定点运算所需要的硬件资源远远少于浮点运算所需要的计算资源。因此,如果将浮点数运算替换成定点数运算,那么,设计ASIC或FPGA就能够有比较高的处理速度,同时获得更高的能效比。然而,这种方法的难点在于如何设计一种数值表示方法使其兼具浮点数的范围与定点数运算的简便。这个领域的学者多采用定点数的方案,这种方案在网络规模较小时尚能取得较好的效果,但是当网络加深,维持原精度所需的数值长度就会快速增长。
上述2种方案还有一个共同的缺陷,它们都需要重新训练,不利于快速部署模型,同时也不够灵活,优化效果因网络模型而异。因此,本文提出一种基于块浮点数[19]的数值表示方案,块浮点数是一种兼具了浮点数的表示范围和定点数的运算复杂度的表示形式,而且基于块浮点数的优化也不需要重新训练网络,使得网络调整和部署非常方便。
2 基于卷积神经网络的特征提取
2.1 损失函数
孪生网络是一种用于衡量2个输入相似程度的网络,它将2个输入映射到新的特征空间中,实现输入的特征提取并在该特征空间中计算相似程度。它的特点是有2个权重共享的特征提取网络,同时输入2幅图片,分别经过2个特征提取网络后,计算特征之间的距离,以此来判断2幅图片之间的相似程度。孪生网络使用Contrastive Loss,该目标函数一方面尽量减小属于一个类别的2幅图片(正样本)之间的距离,另一方面尽可能加大不属于同一个类别的图片(负样本)之间的距离,它的计算公式如下:
其中,d为2幅图片特征向量之间的距离,一般定义为欧氏距离,计算公式如下:
d=||an-bn||2
margin是需要设定的参数,它控制着正负样本距离的分水岭,是后续根据网络输出距离判断输入样本是正样本还是负样本的重要参考。y是样本标签,等于“1”时表明是正样本,此时损失函数的值为距离平方,因此起到最小化正样本之间距离的作用;y等于“0”时,表明为负样本,此时损失函数中的后半项起作用,当网络计算出负样本之间的距离大于阈值时,损失函数达到最小值,因此可以起到将负样本之间距离拉伸到阈值之上的作用。本文设定margin值为0.75。
2.2 特征提取网络
VGG[20]系列网络在2014年ILSVRC竞赛亚军迁移学习等任务中表现优异,同时也是提取图像特征的首选网络之一。本文采用VGG16作为特征提取网络,VGG16包括13层卷积层和4层最大池化层,足够多的卷积层使得该网络能够提取到高级语义信息,较小的kernel size使得最后一层卷积层的感受野也在合理范围内。
为了支持不同尺寸的图片输入,方便适应不同机器人的计算能力,本文去除VGG16中的全连接层,并将最后一层最大值池化层替换成了混合全局池化层,借助全局池化层将最后一层卷积层的输出变成了向量,作为图片描述子。
2.3 混合全局池化层
文献[21]提出了一种拓展的局部池化层,结合了最大值池化和平均值池化的优点,在图像分类任务上取得了明显的提升,并且引入的额外参数和计算量都非常小。本文借鉴这种拓展的池化层的思路,改进了全局池化层,成功应用在回环检测任务中。拓展的全局池化层(Mixed Pooling, MXP),计算公式如下:
fmix(x)=a·fmax(x)+(1-a)favg(x)
其中,
可见,当a取1时,MXP层的表现为最大值池化,当a等于0时,MXP的表现为平均值池化。在进行梯度更新时,后传公式为:

其中,1[·]表示括号内等式成立时取1,否则取0。
3 基于块浮点数的卷积神经网络加速
3.1 块浮点数的定义
使用块浮点数表示数值时,隶属于同一个块的n个数共享同一个乘数因子,称之为块指数。块指数是由n个数中绝对值最大的数确定的,并且,其余的数将会进行移位操作向绝对值最大数对齐。确定块指数并对齐其他数的过程称为块化。
为简化后续行文表述,在此预先引入一些符号,同时使用数学语言阐述块浮点数的定义。对于某一群数,记作X,xi是X中的第i个数,xi的尾数部分和指数部分分别记作mi和ei。对X进行块化后结果记为X′,该块的尾数部分和块指数分别表示为M′X和εX。以下举例说明块化过程,给定一个包含有N个数的块X,可以表示为:
X=(x1,…,xi,…,xN)
=(m1×2e1,…,mi×2ei,…,mN×2eN)
使用块浮点数表示时,X块化为X′,写作:
X′=(x′1,…,x′i,…,x′N)=M′X×2εX
其中:
M′X=(m′1,…,m′i,…,m′N)
εX是块X中最大的指数值,mi是各个块中各个元素对齐后的尾数部分,它是根据下式计算的:
m′i=mi≫(εX-ei)
其中,a≫b表示将a向右移动b位。
3.2 块浮点数矩阵乘法数据流
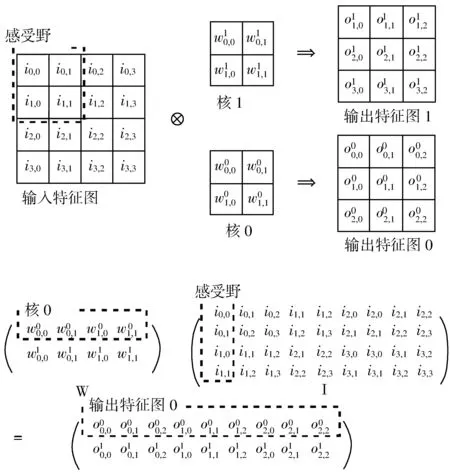
图2 卷积运算展开为矩阵乘法
为了更好地理解块浮点数在卷积神经网络中的应用方式,本文首先介绍一种将卷积运算变换为矩阵运算的方法。在转换为矩阵运算后,卷积核和输入特征图展开为2个矩阵,分别记作W以及I。具体来讲,归属于同一输出特征图的卷积核展开成W中的一个行向量,归属于同一个输出像素点的输入特征图中对应的感受野组成了I中的列向量。如图2所示,输出矩阵O的第m行、第n列元素对应着第m个卷积核在第n个感受野上卷积对应的输出。需要指出的是,将卷积运算转换为矩阵运算的开销是不容忽略的,在高性能CNN加速器的设计中,都采用的是按照卷积方式读取数据流[22]。在本文中,采用矩阵的形式进行计算的目的是方便核心思想的表达,不需引入复杂的数据调度。
为说明矩阵W和I块化的过程,考虑最简单的例子,令:
W=((1.00)2×2-1(1.01)2×20)
分别将矩阵W和I的块尾数字长记作LW和LI,并均赋值为3(不包括符号位)。扫描矩阵I中的元素,得到块指数为εI=2,然后对矩阵I中的元素进行移位并使用四舍五入法处理最后一位,那么,块化后的结果为:
类似地可以得到矩阵W的块化结果为:
W=((0.10)2(1.01)2)×20
因此,对矩阵W和I的乘积,记作O,可以近似为:
O≈W′I′=2M′O
其中,M′O=M′WM′I,εO=εW+εI。
在计算M′O=M′WM′I的过程中,为避免溢出和运算器位数不足导致的舍入误差,需要保证乘法器字长大于等于LW+LI+2,此字长包括符号位在内;加法器的字长不小于LW+LI+S,其中S=floor(log2(K)),以防止加法过程中溢出。具体流程如图3所示,图中“FP2BFP”“BFP2FP”分别代表块化和从块浮点数转回浮点数。
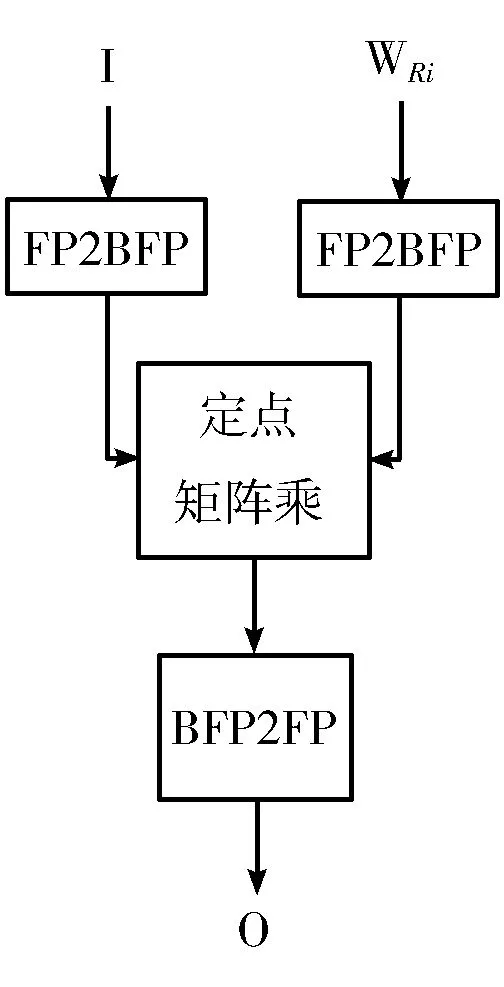
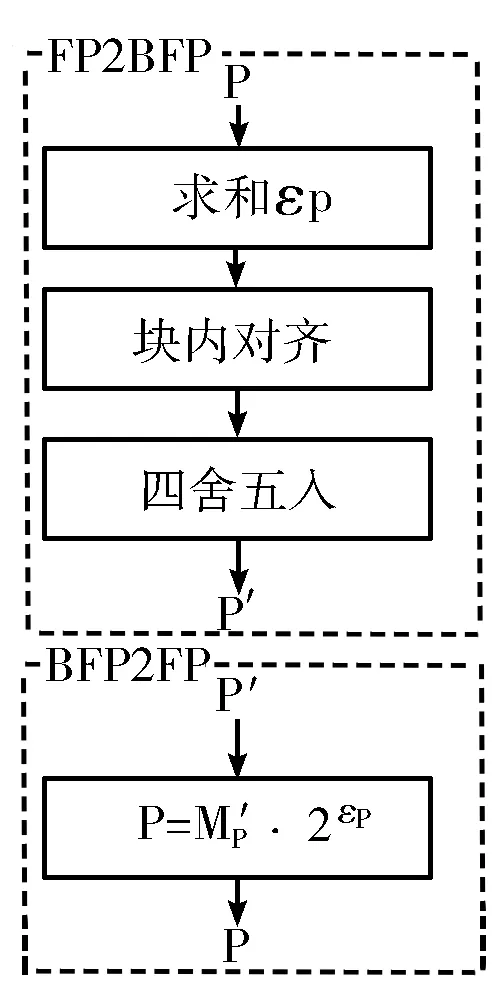
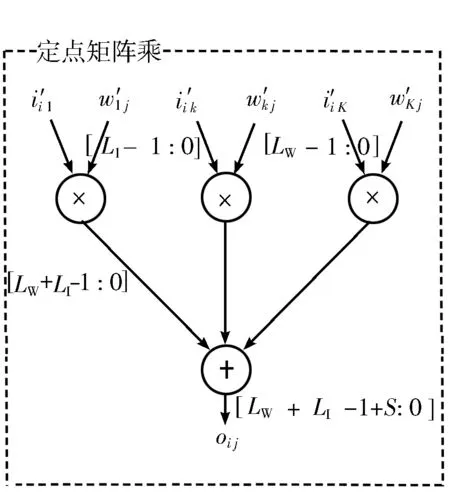
图3 块浮点数矩阵乘法流程
4 实 验
4.1 数据集
本文采用文献[1]提供的训练集sfm120k和测试集Oxford5k、Paris6k。训练集与测试集都隶属于一个大型地标建筑图片集,该数据集包括740万幅图片,利用这740万幅图片进行3D重建,去除3D模型中重复的部分剩下大约16万幅图片,再去除Oxford5k和Paris6k的相关图片,保证训练集中不包括任何测试集图片,最终训练集中包括大约12万幅图片。回环检测与图像检索任务有很多共同之处,他们都是基于图像内容进行图像检索,但是回环检测任务也有其特殊性,回环检测需要考虑一定程度的尺度不变性和旋转不变性。因此,本文对数据集做了数据增强,具体来说,在读取数据集时,对数据集中的图片进行了随机射影变换,以增强特征对射影变换的鲁棒性;同时,对查询图片进行了尺度变换,以增强对尺度变化的鲁棒性。
本文使用ImageNet[23]上预训练好的模型作为模型权重初值,然后在sfm120k数据集上进行调优(finetune)。在调优该网络时,设置基础学习率为1e-6,冲量设置为0.9,惩罚系数为1e-4,迭代100个epoch。在本文中,Contrastive Loss的输入为2个归一化之后的向量和标签,而2个归一化的向量的欧氏距离与余弦距离存在一定的映射关系,具体如下:
Deu=∑(ai-bi)2
=2-2cosθ
4.2 输入图片尺寸对精度及时间的影响
由于图片尺寸大小会直接影响到特征提取所需要的时间,本文首先研究图片大小对精度(mean Average Precision, mPA)的影响,方便移动机器人根据自身的计算能力挑选合适的图片尺寸。图片尺寸越大,保留的细节越多,回环检测的精度就越高,但也会更耗时;图片尺寸越小,丢失的信息越多,对应着精度就会降低,但更能适应移动平台的计算能力要求。在GeForce RTX2070上测试的结果如表1所示。

表1 图片尺寸与耗时、精度(mAP)关系
在实验过程中,图片大小重整为最长边不超过图片尺寸所列数值,用时包括了特征提取和查询的时间,完整地模拟了回环检测过程。可以看出,1024 px的图片达到了最高的准确度,但是需要超过60 ms的处理时间,勉强接近SLAM的实时性要求。但是移动机器人上往往难以提供RTX2070所能提供的计算能力,因此1024 px的图片难以直接应用在移动机器人上。尺寸更小的图片虽然速度更快,但是精度损失过大,如224 px的精度损失接近30%,大幅降低了性能。512 px的图片处理时间为18.4 ms,假设移动机器人能够提供的计算能力为RTX2070的一半,512 px尺寸的图片也可以保证实时运行,同时,精度下降在可接受范围内,因此本文选用512 px尺寸的图片进行后续实验。
4.3 不同池化层的影响
本节对比分析多种不同的池化策略对回环检测精度的影响。选取GeM[1]以及直接使用最大值池化(max)和均值池化(mean)作为对比,还选取一种非参数化为特征图各个维度加权的方法(Cross-Dimensional Weighting, CDW)[24]作为对比。GeM是当前世界领先的图像检索算法,以下先简要介绍GeM和CDW方法。
GeM的结果由以下公式给出:
由上式可以看出,通过学习参数Pk可以令fGeM表现出不同的行为,Pk取0和∞对应着平均池化和最大值池化。但是,如上式所示,该方法引入了大量指数运算,对于移动计算平台来说,开销较大。
CDW是一种非参数化的方法,从纹理出现频次的角度出发,笔者认为,出现频次越少对图片检索的重要性越高,表现在特征图上即该特征图上0的比例越高,该特征图就应当有更高的权重,另一方面,笔者还考虑到了各个感受野上特征种类分布,如果该感受野上特征种类越多,即特征越丰富,在不同的通道上都有响应值,表明该位置应该有较高的权重。
在文献[1]的基础上,本文实现了MXP和CDW,并分别对他们进行了调优,同时,选取最大值池化和均值池化作为比较基准,也进行了调优。表2列出了不同策略对最终精度的影响,可以看出GeM的精度相对最高,本文所用的MXP次之,在不同的数据集上互有优势,效果相当。CDW相对均值池化取得了不错的提高,但是不如GeM和MXP。最大值池化表现比均值池化更好,这可能是因为最大值池化更关注最突出的特征,比均值池化具备更高的表达能力。rOxford5k和rParis6k是按数据集原有4等级进行了划分,除第4等级完全没有目标图片外,其余3个等级分别对应着表中的E、M、H这3项,表示回环检测的难度为容易、中等和困难,如表2所示。

表2 rOxford5k、rParis6k上的精度(mAP) 单位:%
从表3可以看出,MXP和GeM在不同的数据集上有不同的表现:MXP在Oxford5k上的表现优于GeM,在Paris6k上则不如GeM。这主要是2个数据集图片特征差异引起的:Oxford5k中的图片大多纹理复杂,有相当多的重复特征,此时最大值池化可以抛弃许多不显著的细节,表现更好,如表3中max远远好于mean,甚至好于CDW;而Paris6k则恰好相反,其中图片大都背景空旷,此时使用max会导致纹理丢失,因此在该数据集上max与mean精度相当,不如CDW表现好。由于MXP是max和mean的线性组合,并且max在MXP中占有更大比重,因此在mean也能提取重要信息的数据集上,如Paris6k数据集上表现不如GeM。另一方面,GeM可以认为是max和mean的非线性组合,在max和mean均有贡献的数据集上表现更优,在只有max可以提取有效信息的数据集上反而会受mean的负面影响。

表3 Oxford5k、Paris6k上的精度(mAP) 单位:%
4.4 加速后的回环检测精度
本文在CPU上模拟了块浮点数(权重矩阵块尾数与输入特征图矩阵尾数均为8位,包括符号位)的计算过程。并将PyTorch模型转换为Caffe[22]模型,测试结果如表4和表5所示,与表2、表3相比,几乎没有任何精度损失,表明了加速方案的可行性。

表4 加速后Oxford5k、Paris6k上的精度(mAP) 单位:%
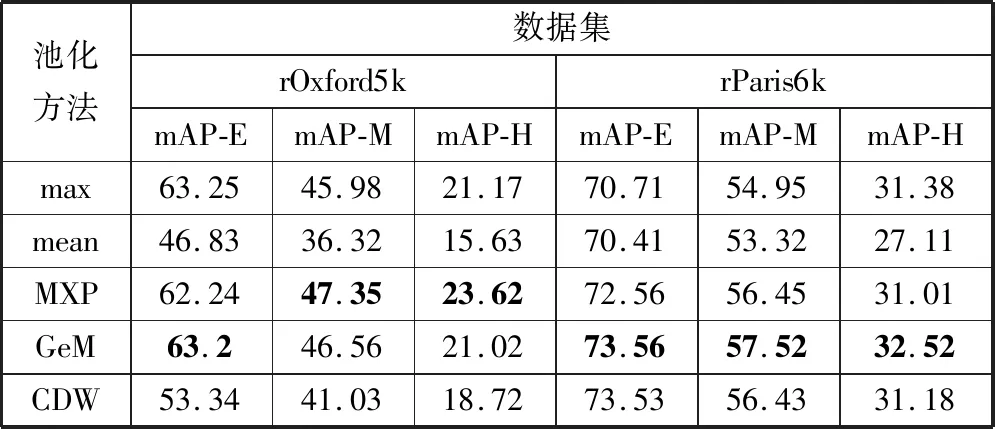
表5 加速后rOxford5k、rParis6k上的精度(mAP) 单位:%
5 结束语
通过对比分析多种不同的将特征图转变为特征向量的方法,可以发现本文使用的混合全局池化方法计算简便、硬件实现简单并且精度与复杂的池化方法相当,表现出了良好的性能。本文提出的基于块浮点数的深度学习加速技术能够将卷积中的浮点运算转变为定点数运算,降低了对运算资源的要求,并且对精度的影响很小。

