基于信道特征和随机插值的物理层算法
吴 游,陈 诚,金 龙
(江苏科技大学电子信息学院,江苏 镇江 212000)
0 引 言
随着信息时代与电子科技的飞速发展,无线通信因其灵活性、开放性等特点被广泛应用于军事和民用领域,然而无线通信系统中传输媒介的广播特性和不稳定的网络结构会使其安全性面临非常严重的威胁[1-3]。以往的解决办法是在链路层及上层利用密钥对数据实施加密,但是在动态无线网络系统中,对称加密将会面临密钥分发的难题。此外,传统加密方式基本是基于有限的计算资源难以在秘密信息的时效期内对其破译。随着量子计算机的诞生,其较快的运行速度和强大的信息处理能力将使传统加密方法不再安全[4],因此,人们迫切需要找寻一种理论上牢不可破且在实际应用中切实可行的安全机制。
当前,无线通信系统的安全策略均建立在链路层及链路层以上,而较为重要的物理层存在一定的漏洞[5]。近年来,一些物理层安全方案[6-8]相继被提出,表明物理层安全正逐渐受到人们的重视。文献[9]提出了一种基于相位旋转和小波变换的物理层安全噪声伪装方案,利用空闲带宽中的宽带噪声信号作为传输数字信号的载体,使调制后的信号与环境噪声相似,能够隐藏在无线环境中难以检测。仿真实验的结果表明,该方法对授权接收机具有较高的可靠性,对窃听者具有良好的保密性。文献[10]提出了通过扰乱正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)系统星座映射符号实现对传输信息加密的物理层安全方法。该方法能提供较好的安全性,但不足之处在于串行的扰码矩阵生成方式会给算法的实现复杂度及加密速率带来不利影响。在文献[11]中为保护OFDM调制过程而选择大量酉矩阵当作控制密钥,不仅使系统的峰均比得到改善,而且也提升了安全性。然而该方法往往将密钥值选择得太大,给密钥传输和存储造成困难。
现有的及新一代的无线通信技术都采用OFDM调制方式,其强抗干扰能力和高频谱利用率的特点符合无线通信业务的需求。然而过往的研究并没有很好地结合OFDM并行调制的特性,在算法的实现上比较繁琐,不能满足当前的宽带高速无线通信系统对高速率的要求。因此,本文从物理层安全角度考虑,提出一种基于OFDM调制特点的新安全算法,利用无线信道特征生成共享密钥,在多路低速并行的数据上完成数据符号随机插值加解密,极大地减小了该算法实现的复杂度。理论分析和仿真表明该算法不会对系统的原有性能造成负面影响,且对各种窃听攻击抵御能力较强。
1 无线信道的密钥生成方法
现有研究得出,短时互易性、时空唯一性、快速时变性和不可预测性是无线信道具有的主要特性,为基于无线信道特征的密钥提取方案提供了理论依据[12-17]。基于无线信道特征的密钥生成方法利用信道的互易性等特性,使合法通信双方可独立同时生成相同密钥并频繁更新,不仅可以避免密钥传输,成功解决密钥管理难的问题,而且只需结合一些非常简单的加解密算法就可提供必要的安全性,更适合将来的高速无线通信系统[18]。已有学者对无线信道在不同环境中进行了测量,验证了将信道特征当作随机源获取共享密钥的可行性[19-21]。当前生成共享密钥的主要过程如图1所示,具体包含以下步骤[4]:
1)信道估计。在时分双工(Time Division Duplexing, TDD)模式下,合法通信的双方Alice与Bob在相关时间内先发送训练序列到对端再测量信道的某些特征,如信道冲激响应(Channel Impulse Response, CIR)、接收信号强度(Received Signal Strength, RSS)等来提取两者之间无线信道随时间的变化值[22],由于噪声等因素的影响,提取的信道特征高度相关但不完全相同。
2)量化。把测量的特征值用不同量化方法转变成一串二进制密钥比特。
3)密钥协商。按照某种信息调和协议来纠正或丢弃通信双方获取的密钥差异。
4)密钥增强。进行密钥一致性校正,舍弃部分一致的密钥比特或采取某种比特转换用来增强密钥,增大密钥熵的同时模糊非法通信方在之前密钥协商的过程中有可能获得的部分信息。
多轮协商仍无法达成一致的初始密钥会被丢弃,因此,经过协商和一致性校验后最终生成的加解密密钥必然满足完全一致性。
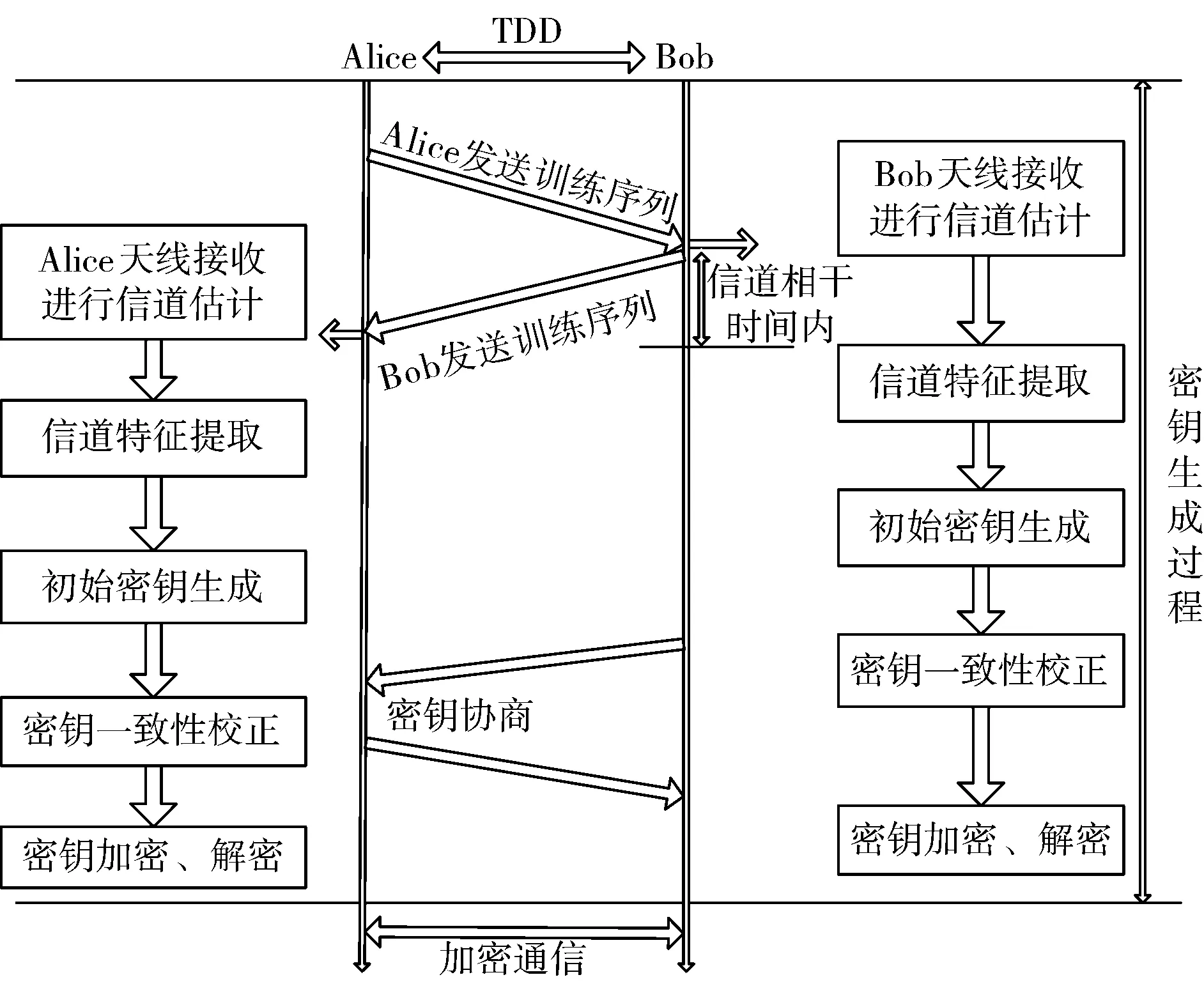
图1 共享密钥生成流程
现行密钥生成算法有很多,本文针对文献[23]中传统的多比特自适应量化(Multi-bit Adaptive Quantization, MAQ)算法选取所有特征值进行量化导致初始密钥不一致率较高的弊端,提出一种m窗口筛选机制对特征序列预处理的方案,如图2所示。只有连续m个或大于m个特征值才能保留为一个特征值。图中ha和hb为合法通信双方所提取的信道特征序列,l为量化比特数位。仿真表明改进的MAQ算法提高了密钥生成速率且大大降低了初始密钥的不一致率。
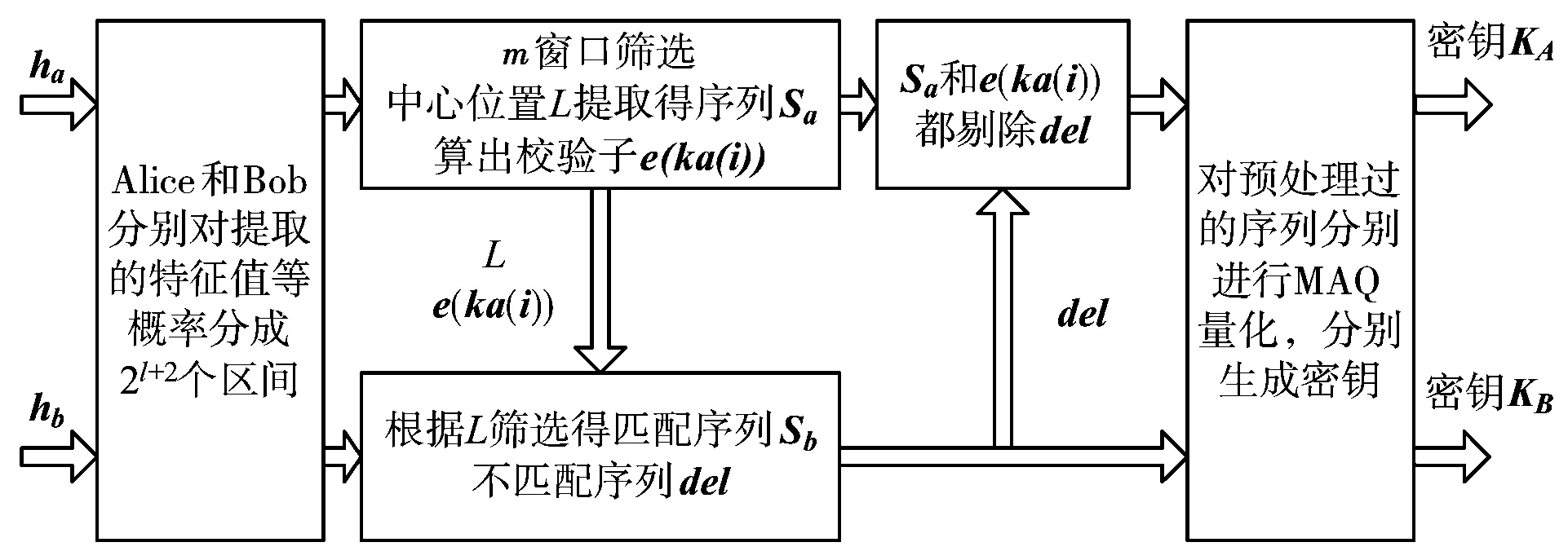
图2 改进的MAQ算法方案
2 OFDM系统插值加解密算法
2.1 算法基本原理
根据OFDM调制过程的特点,本文提出一种基于随机插值的物理层加解密算法,如图3所示。该算法的主要思想是利用在快速傅里叶逆变换(Inverse Fast Fourier Transform, IFFT)后输出的数据符号中随机插入部分数据符号的方式,对原OFDM符号插值加密重构,使得非法用户难以有效破译,实现对信息的安全保护。
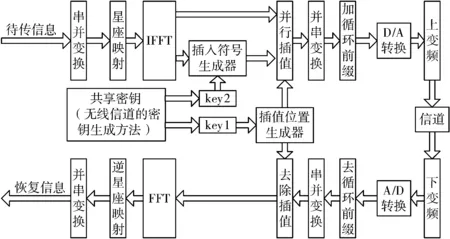
图3 OFDM系统插值加解密算法原理
本文算法的实现包含密钥生成、插入位置生成和插入符号生成等重要过程,其余与OFDM各环节基本相同,如IFFT前的串并变换及星座映射,IFFT后的并串变换及添加循环前缀(Cyclic Prefix, CP)等。首先确定好计划插入的数据符号个数L;然后利用密钥key1产生L个插入位置;再利用密钥key2另外生成L个位置,并将原OFDM符号中对应位置的L个数据符号取出,得到插入符号向量;最后依据插值位置将确定好的插入符号按次序插入即可完成物理层加密。解密时,合法通信方只需根据密钥key1逐个去除插入的符号便可。
2.2 插值位置和插入符号的生成过程
插值位置向量和插入符号向量的生成方式如图4所示。前文已提到基于无线信道的密钥生成方案使合法通信双方可独立同时生成相同密钥并频繁更新,无须进行密钥传输。将生成的共享密钥(二进制比特串)以log2N(N是OFDM系统的子载波数)为分组长度进行分组取值;然后将与2倍插值符号数量相等的2L组取出,前L组组成key1,后L组组成key2,接着完成由二进制~十进制的进制转换,得到[0,N-1]之间的整数。将由key1得到的L个整数从小到大排序,即生成插值位置向量A,A=[A0,A1,…,AL-1]。由key2得到L个位置向量,取原OFDM符号中对应位置的L个数据符号,形成插入符号向量B,B=[B0,B1,…,BL-1]。
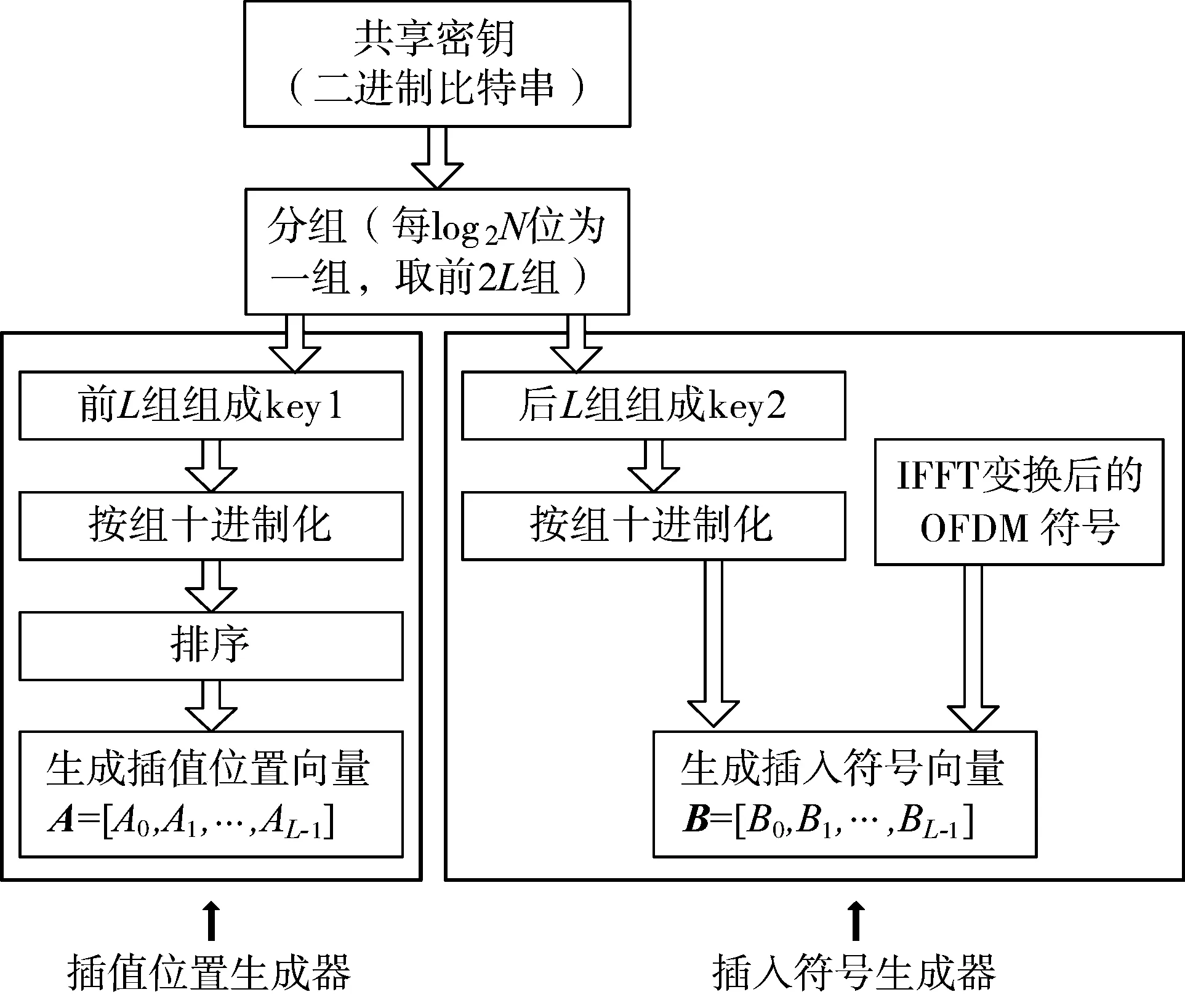
图4 插值位置和插入符号的生成过程
2.3 插值加解密算法主要流程

图5 随机插值加密算法流程
安全算法的加密操作过程如图5所示,步骤如下:
步骤1得到未经加密的OFDM符号。N为子载波个数,符号首先通过串并变换、星座映射,转换后生成复数列向量X,X=[X0,X1,…,XN-1]T,X为IFFT变换的输入信号。再对X做IFFT变换后得到复数列向量Y=[Y0,Y1,…,YN-1]。
步骤2确定好计划插入的数据符号数量L,然后生成密钥key1、key2。
步骤3在key1的控制下得到插值位置向量A,A=[A0,A1,…,AL-1]。
步骤4在key2的控制下产生L个位置向量,取原OFDM符号中对应位置的L个数据符号,形成插入符号向量B,B=[B0,B1,…,BL-1]。
步骤5依据插值位置向量A,把插入符号向量B中的值按次序插入,得到加密后的OFDM符号向量Y′,Y′=[Y0,…,B0,…,B1,…,BL-1,…,YN-1]。
步骤6将加密后的OFDM符号向量Y′添加CP发送出去。
解密时,合法接收方只需根据密钥key1确定加密时插入符号的具体位置,依次去除插入的数据符号就能实现OFDM符号的解密工作,进而成功得出传输的原始信息。
2.4 算法的相关理论分析
1)算法的加密效率。本文方法是利用IFFT变换后随机插入数据符号来完成OFDM符号的加密。整个过程是在多路并行低速数据上进行,并行符号时间周期至少是输入数据时间周期的N倍。插入的数据符号是计算IFFT变换后的相应位置的符号值,计算量小,操作简便。本文算法拥有较高的加密效率,因为其利用的是并行输出时的富余时间来完成简单的插值操作。
2)算法对系统同步的影响。载波同步及时间同步是OFDM系统的2种同步技术。本文算法对IFFT变换后的数据符号进行随机插值加密,在接收端,先去除插入的符号,再完成快速傅里叶变换(Fast Fourier Transform, FFT)的解调过程,因而载波同步不会受到干扰。安全算法中先进行插值加密,再插入CP,因此利用CP和导频信号来估计定时同步也同样不会受影响。
3)算法对系统带宽的影响。IFFT变换后,在OFDM符号中随机插进若干数据符号的做法,一定程度上扩展了时间域,使加密后的OFDM符号周期变长,另一方面也等同于增加子载波数,使频谱得到扩展,因此系统的带宽会增加,并且增加的带宽和插入符号的数量成正比,同时插入符号的数量也与算法的安全性紧密相关。为了在确保安全的前提下,尽可能减少带宽的增加,本文将通过仿真实验来确定插入符号数量。
4)算法的密钥空间。将L个数据符号插入长度为N的OFDM符号中,N为子载波数。若插入位置不重复,共有N!种可能,即密钥空间达到了N!,N!=N·(N-1)·…·(N-L+1)。若插入位置可重复,可能性有NL种,此时密钥空间的大小应为NL。如N=64、L=12时,2种方式的密钥空间经计算分别为270和272。密钥空间越大算法越安全,本文算法显然具有较大的密钥空间,因此具有较高的安全性。
3 仿真实验和分析
仿真实验主要采用64个子载波、正交相移键控(Quadrature Phase Shift Keying, QPSK)星座映射方式的OFDM系统。信道为2径Rayleigh衰落信道,最大多普勒频移为100 Hz,信道上叠加高斯白噪声。加解密时,密钥取自基于合法通信双方无线信道特征生成的共享密钥,按改进的文献[23]MAQ算法生成。
3.1 算法安全性受插入符号个数的影响

图6 子载波数为64时,OFDM符号解调后的误符号率
插入符号个数的多少会对算法的安全性造成影响,只有合理确定插入符号的数目,才能让算法拥有比较好的安全性能。实验过程中的误符号率是根据对6000个OFDM符号的统计得出的。仿真结果如图6所示,其中横坐标表示插入符号的数量,纵坐标表示非法用户解调后的误符号率,非法用户采用随机密钥解密。由图6可知,初始阶段随着插入符号数量逐渐增加非法用户的误符号率不断变高,此后保持在75%以下并趋于平稳。当插入符号为8个时,误符号率变为60%左右;当插入符号为16个时,误符号率变为70%左右;当插入符号超出16个时,误符号率就不会明显增长,始终处在70%~73%之间。理论上QPSK星座映射随机猜错的概率是75%,当插入符号超出16个时,非法通信方能够成功解调得到原信息的机率已近乎随机猜测。因此,插入太多数据符号并不能显著提高安全性能,反而会造成峰均比和系统带宽增加的不利影响。为了尽可能少地在增加带宽的前提下实现算法的安全性,插入符号数量可控制在8~16个,非法用户的误符号率将始终处于60%以上。不同子载波个数的OFDM系统插值个数参考如表1所示。

表1 不同子载波个数的OFDM系统插值个数参考
3.2 安全算法抗攻击能力仿真分析
信息在自由空间中是以连续信号的形式进行传输。合法用户在接收端利用导频及循环前缀完成定时同步后,会截取一个周期为T′的OFDM模拟信号。由采样定理可得长度为N+L的OFDM离散符号,采样间隔为T′/(N+L)。解密时由密钥key1控制插值位置生成器获得插入符号的位置信息,直接去除插入的数据符号便可完成OFDM符号的解密。而非法用户窃取到加密后的OFDM符号时会面对2类情况:1)并不知晓有符号插入;2)确定插入L个符号,却不清楚具体位置。
3.2.1 未知有符号插入
设原OFDM符号周期为T,采样间隔TS=T/N,则T=NTS,系统带宽B=(N+1)/(NTS),则TS=(N+1)/(NB)。IFFT后随机插入L个数据符号时,OFDM符号周期变为T′=NTS+LTS=(N+L)TS。此时在窃听端,由于不知道有符号插入,在完成定时同步得到一个周期的模拟信号后,非法通信方会忽视插进的符号向量,并直接对信号做相应处理。先通过分析接收信号的频谱得到带宽B′,亦或是分析信号的持续时间获得周期T′,然后根据子载波数N,就会得到错误的采样间隔TS′=(N+1)/(NB′)或TS′=T′/N,而正确的采样间隔应为TS′=(N+L+1)/[(N+L)B′]或TS′=T′/(N+L),采样间隔直接关系到子载波间的正交性和能否正确解调。所以按照错误的采样间隔对接收信号离散化,子载波间原有正交性无法保持,非法用户难以恢复信息。表2是该情况下实验仿真后得到的误符号率信息,插入符号数为8~20个。从表2可清晰看出误符号率均在60%以上,由此说明在忽略插入符号直接进行相关处理的方式下要想破译出传输信息是极其困难的。

表2 未知插值加密情况下的误符号率信息统计
3.2.2 已知有L个数据符号插入,但不清楚位置
该情况下非法用户的破译方式有2种:1)在FFT前将L个符号随机去除,这会导致原符号的排列顺序和大小分布被打乱。由OFDM子载波之间的叠加特性可得,该做法也必将严重破坏子载波之间的正交性,随机去除的方式必然会对原信号造成巨大影响,使FFT后恢复出来的信息严重失真。2)即不去除插值,直接将加密后的符号进行FFT变换。虽确保原子载波间的正交性不会被破坏,但解调得到的符号有N+L个,原信息符号数目仅为N个,使得非法通信方很难做出选择。
1)FFT前随机去除。因为符号插入位置由密钥key1控制,在无法获知密钥的前提下,为破译信息,非法用户只能对密钥采取随机猜测的方式,根据猜测的密钥确定插值位置。表3为该情况下的误符号率统计表,L取12,分别统计非法用户在随机序列生成的7个随机密钥下的误符号率。由表3可知误符号率均维持在60%以上,因此,随机去除插值的破译方式无法对信息传输产生较大的安全影响。

表3 FFT前随机去除时的误符号率信息统计
2)先FFT后再去除。非法用户对截取的长度为N+L的OFDM符号,先不解密直接进行FFT变换,然后对变换后的符号随机去除L个。表4是非法用户在该情况下的误符号率统计,从表4可看出非法用户的误符号率始终在70%以上。表中还存在某些误符号率大于75%的情况,主要是因为对插值加密后的符号先FFT然后进行插入符号的去除,会造成输入符号不再满足等概率分布,误符号率也随之上升。所以该方式下非法用户同样无法获得正确的传输信息。

表4 FFT后随机去除时的误符号率信息统计
3.3 安全算法对OFDM峰均比的影响
由于插入的数据符号取值于原OFDM符号,因而不会产生新的峰值功率,所以信号原有的平稳性基本可以得到维持。图7是OFDM符号插值加密前后峰均比(Peak to Average Power Ratio, PAPR)的互补累积分布函数(Complementary Cumulative Distribution Function, CCDF)仿真图。从图7可看出这几条曲线十分接近,所以插值加解密算法不会对OFDM符号本身造成明显的峰均比的影响。随着插入符号数量的增加,OFDM峰均比会略有增加。毕竟插值加密等同于增加了子载波数,而子载波个数N越大则峰均比高出某个门限值的机率也就越大。只要适当控制插入数据符号的个数,原有系统的峰均比就不会受到明显影响。

图7 插值加密前后峰均比对比
3.4 安全算法对多径信道模型的适应性分析
OFDM系统的主要优点是各子载波之间相互正交,同时循环前缀的添加也有助于消除子载波之间的干扰及符号间干扰,使得通信系统具备良好的抵抗多径衰落的能力。图8是原OFDM符号和插值加密后的OFDM符号分别通过2径衰落信道并加入高斯白噪声后的误码特性曲线。从图8能清晰地得出,通过信道模型之后,在信噪比不超过4 dB时,插值加密后的OFDM符号同原OFDM符号的误码性能曲线近乎重合,当信噪比超过4 dB的时候,加密之后的OFDM符号整体误码率要低于原OFDM符号。因此,在误码性能上,采用插值加解密算法会比原系统有一定的改善,其抗多径衰落及噪声干扰的能力得到了提高。这是因为多径效应可造成信号衰落,多径及噪声的干扰导致部分符号产生错误,如果错误的符号之中恰好有插入的符号,在接收端解密时将插入的符号去除后,就能够减小多径及噪声的干扰。由此可见,基于OFDM调制特点插值加密的新方案对噪声和多径衰落信道有较好的适应性,且从图8上可以看出,调制过程中即使采取不同的星座映射方法也不会对系统误码性能产生不利影响。
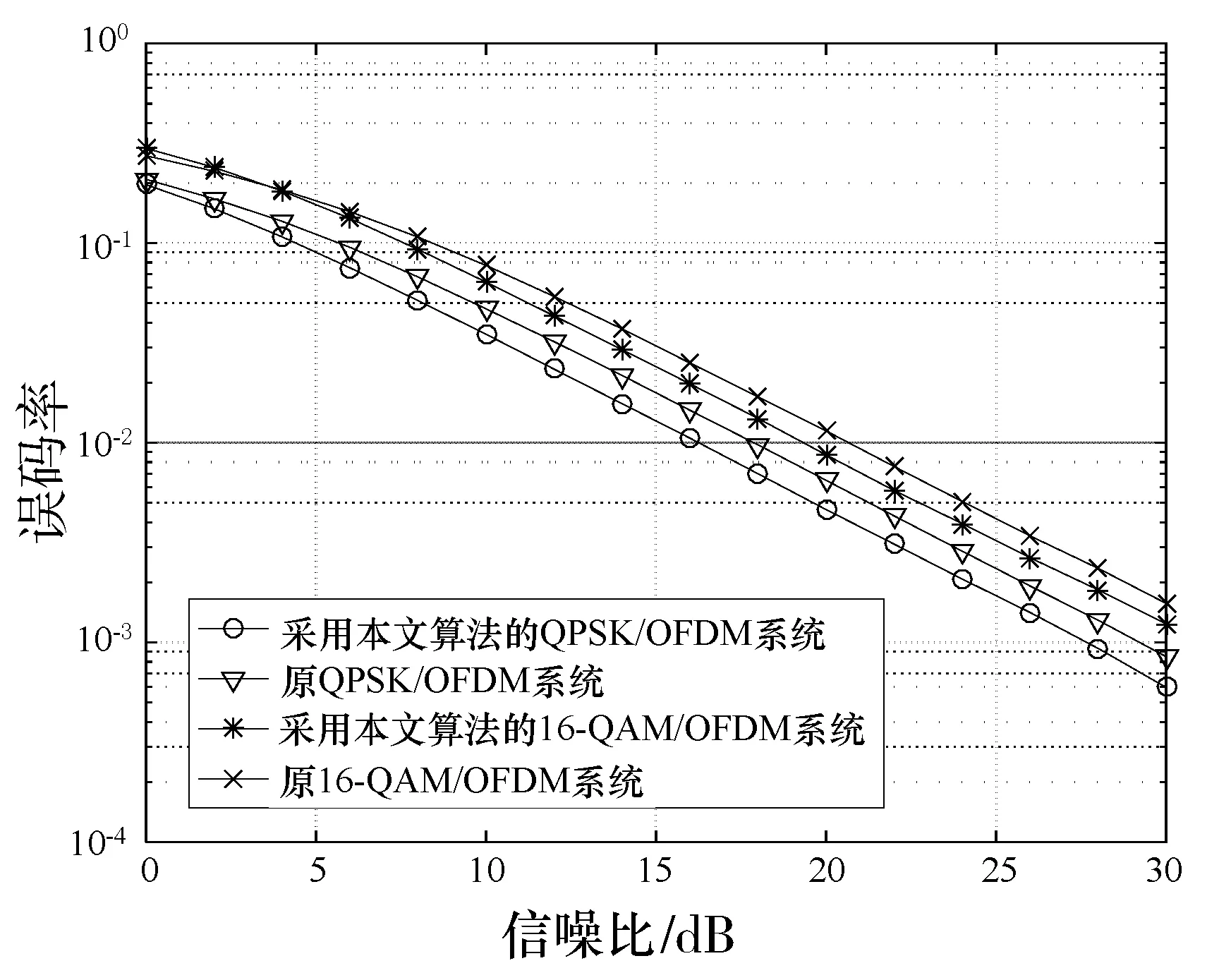
图8 加密前后多径信道下的误码特性曲线
4 结束语
现有的物理层安全算法通常都是针对信道加噪、相位旋转等具体特点提出的,属于串行加密方式并不适合4G乃至未来5G的高速传输系统。以往针对调制方式加密的相关研究也多是利用混沌序列产生伪随机加解密序列的方式应用到保密通信中,虽然混沌序列具有较好的伪随机性,作为通信密钥的序列生成器初值却有泄密的风险,一旦被窃听方获取,通信的安全性将无从保证。基于无线信道特征生成的共享密钥无须进行密钥传输,密钥无任何泄露风险,随机性强且更新频繁,窃听方根本无从破译。本文根据OFDM技术相关原理,提出了同OFDM调制特点相结合的并行插值的物理层安全算法。新算法利用共享密钥加密调制的过程,通过对IFFT的输出数据符号随机插值实现数据安全。理论分析及仿真实验均表明该算法可实现对信息的整体加密,具有可靠的安全性。与现有的物理层算法相比,并行插值方式会有效减小系统实现的复杂程度。安全算法仅仅略微增加了些带宽,对系统的原有性能如误码率、峰均比等影响较小,在多径信道中展现出了很好的适应性。本算法实现过程简单且采用并行符号加密方式非常适合当下及未来的高速传输系统。

