基于时间稳定性和降维因子分析的土壤水分监测优化

闵俊杰，蒋立新

(1.国电环境保护研究院有限公司，南京 210031；2.无锡市城市防洪工程管理处，江苏 无锡 214000)

1 研究区域的概况和方法

1.1 研究区域的概况

本次用于研究的区域属于亚热带的季节气候，每年的四季比较分明，且气候属于温和，每年的平均气温均保持在16℃左右，而每年的降水量则为1203.5mm，一年的降雨基本维持在6月至9月间，此时段的降雨量点全年的60%，年日照数则为2137.6h，本区域内的光热能量十分充足，对农作物的生长非常有利。本地区的海拔则牌15-35m间，属于低丘倾斜的平原地带，两个研究区域平均的坡度大概在12%左右，土地主要用来种茶和竹林，监测点的土壤类型则属于薄层的粗骨土。该土壤的土层比较浅，一般情况下厚度≤1m，并且土质十分松散，其中含有30%的砾石[1]。

通过依据现场的实际情况以及土地的利用性质决定按照8m的间距设立共计77个监测点，在茶园区域内设立39个，具体编号则从1-40号，并且将30号予以空缺，而在竹林区域中设立38，具体编号则从41-79号，并将69号予以空缺。本次监测仪器运用剖面土壤水分的传感器，其主要以是TDR时域反射仪技术，其可以对土壤进行测量介电常数，然后将其加以转变得出土壤中的水份含量。利用剖面土壤水分传感器对监测点进行定期的测量，主要测量深度为10cm、30cm深土壤内的水分，并且每月一次和覆盖干湿季节，对于降雨特别多的雨季更加强监测的资料，比如在5月份的10号和13号以及15号开展监测，未得到监测13号、21号、44号、65号点的30cm位置水分的含量。而在2016年12月到2017年12月间总共测量的14次左右。通过利用在2017年3月到l0月间测量的10次详细数据融入建立样点测量土壤水分回归的模型之中，然后运用2016年12月和2017年1月、11月、12月的4次监测数据对结果进行验证。

1.2 具体研究的方法

研究区域土壤水分的时间稳定性计算公式为：

(1)

(2)

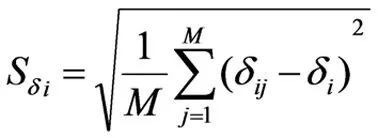
(3)

如果δi=0则表示此监测点代表研究区域内的平均湿润；δi为正值则表示监测点的湿润度要超出研究区域平均的湿润度，δi为负值则与之相反。Sδi越大则表时监测样点的土壤水分时间方面非常的不稳定[2]。

通过以时间稳定性为重要的研究基础，并加以利用统计学软件对所有监测点的土壤中水分的特征进行分析。本次使用SPSS22.0统计软件并采用降维因子进行相应的分析，主要对茶园区域与竹林区域的相关监测点在3月至10月间对土壤进行监测的详细数据加以分析研究，利用主成分相关性的分析方法进而分析得出成分图。在图中一些相关性非常强的监测样点聚集在一起，然后与通过时间稳定性分析得出典型样点加以有效的结合进而选择合理的监测点，最终实现选择的监测典型点可以体现出本次研究区域中全部样点。通过有效的利用逐步多元线性回归(P<0.1)，然后选择自变量为典型监测样点的土壤水分，而因变量则是其它监测样点，由此最终建立用于研究区域典型样点和样点的土壤水分具有关系的相应模型[3]。利用典型监测样点获取的监测数值，并经过关系模型详细的计算，最得出本次研究区域内所有样点的土壤水分含量，然后通过实际的测量数据加以校验，最终对预测结果的精度利用均方根误差开展相对应的综合评定。

2 结果与分析

2.1 时间的稳定性分析

通过对2017年3月到10月间对茶园区域和竹林区域的所有监测点进行监测得来的详细据开展时间稳定性特征的相应分析。研究区域所有样点平均的土壤含水相对偏差具体如图1显示进行分布，对所有样点标准差的标注采取垂直误差线加以显示。土壤内的平均含水相对偏差，茶园区域基本分布-0.5-0.5之间，如图1(A)所示，其中有15个监测点的时间稳定性比较好，其土壤含水相对偏差的标准差是Sδi<0.1；有20个监测点的时间稳定性一般，土壤含水相对偏差的标准差是Sδi在0.1-0.2；有4个监测点的时间稳定性较差，Sδi>0.2。而竹林区域内则主要分布在-0.4-0.4之间，具体如图1B所示，有22个监测样点的土壤含水量具有较好的时间稳定性，13个监测样点时间稳定性则为一般，还有3个监测样点的时间稳定性表现较差。

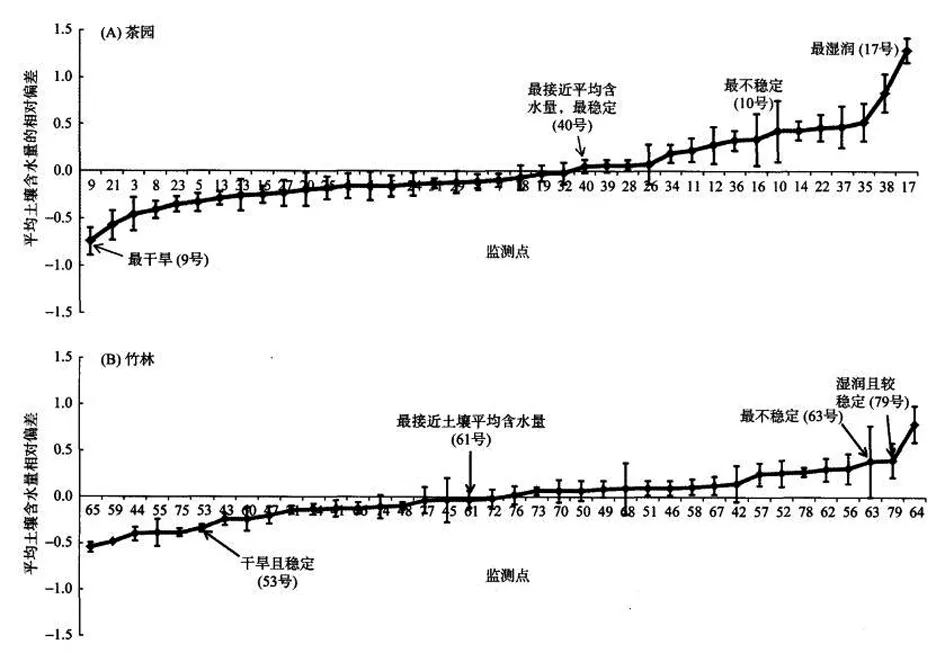
图1 茶园区域(A)和竹林区域(B)监测点平均土壤的水分相对偏差

通过选择茶园区域中的监测点17号较为典型的样点作为湿润的代表，而40号监测点的时间稳定性特别好，其可作为接近土壤水分平均含量的样点，而干旱样点则由9号监测点加以代表；时间稳定性最差的监测样点则由l0号表示。与上述基本相同，在竹林区域内由79号监测点作为湿润的代表，而接近土壤平均含量最好的则为61号监测点，干旱监测样点为53号，时间稳定性比较差的样点为63号监测点、通过以时间稳定性为基础进行选取典型样点4个点建立分析的线性回归模型，其无法有效的对研究区域内的全部监测样点的土壤水分进行精确模拟。本次在茶园区域内，在30cm深处共有22个监测点取得了较好的模拟精度(如表1所示)，而在10cm的位置，有29个监测取得较好的模拟精度，另外还有3个监测样点比较差。在竹林区域内，，在30cm深处共有26个监测点取得了较好的模拟精度，另外还有2个监测样点的精度比较差(如表2所示)；在10cm的位置，有35个监测取得较好的模拟精度，另外还有2个监测样点比较差。由此表时，当分析自变量选择由时间稳定性加以选择的4个典型样点时，无法对研究区域内的所有监测样点的土壤水分进行精确的模拟[4]。

表1 茶园区域典型监测样点回归模型所制定系数R2的分布数据

表2 竹林区域典型监测样点回归模型所制定系数R2的分布数据

2.2 降维因子分析

通过对2017年3月至10月间的10次土壤水分的数据开展降维因子分析而得出图2(旋转空间成分图)。从该图中可以看出，监测样点的位置和其之间的距离远近可以表明监测点具有相关性的高低，经过综合性的考虑和分析所有的监测样点的相关性和典型样点，竹林区域选择的监测样占为55和45号，而茶园区域则选择23和12以及3号。

图2 茶园区域(A)和竹林区域(B)监测点旋转空间成分图

通过在已经选择监测典型的样点为基础之上加以融入利用降维因子进行分析得出的监测样点当作建立回归模型时的自变量，观察回归模型的决定系数R2数据。通过对茶园区域融入添加典型监测样点之后，R2见表1。通过将3号、9号、10号、17号、23号、40号、12号等监测样占当作回归模型的自变量时，在30cm深度位置有29个较好的模拟精度，具体见表1所示，而在10cm深处则有35个较好的模拟精度。并且在总监测中，10cm深处位置和30cm深处位置较好的模拟精度分别占总量的89.7%和78.4%，由此表明可以对本次研究区域内的土壤水分加以有效的监测。

而在竹林区域之中融入55号监测样后，见表2，其在30cm深度位置则有32个监测样点具有较好的模拟精度，在10cm深度位置则有36个监测样占具有较好的模拟精度，以及1个较差的模拟精度。在总监测中，10cm深处位置和30cm深处位置较好的模拟精度分别占总量的94.7%和88.89%，由此表明竹林区域中只有5个监测样点便具有较好的模拟精度。

3 结 论

综上所述，利用时间稳定性与降维因子的结合而对土壤水分展开相应的分析，并选择科学合理的典型监测样点的相应组合，最终可以有效的利用多元线性回归模型对监测点的土壤水分进行准确的模拟。当只运用时间稳定性作为回归模型的自变量时，模拟的精度并不能实现对研究区域内的土壤水分进行准确的模拟，而当时间稳定性与因子进行结合后，建立模型时所选择的典型监测样点可以实现该模型具有非常准确的模拟精度。