基于PCA 和BP 神经网络的中南公路岩质边坡稳定性预测

牛鹏飞，周爱红

(1.河北地质大学 勘查技术与工程学院，河北 石家庄 050031；2.河北地质大学 河北省高校生态环境地质应用技术研发中心，河北 石家庄 050031)

0 引言

随着社会经济的发展，人们对自然资源的需求量越来越大，不可避免地对山区矿山进行开采，特别是沿公路沿线露天开采矿产资源、煤炭资源等，对公路及公路边坡稳定性造成了很严重的影响。 因此，对山区公路边坡稳定性预测具有重要意义。

公路边坡稳定性的状态受多个因素共同影响[1-2]，且影响因素间有较强的非线性关系[3]，所以对预测模型的挑选更加严格。 长期以来，针对公路边坡稳定性的预测研究，国内外专家学者们提出了众多的预测模型[4-8]，并取得了良好的效果。 但由于影响因素的随机性和时效性，难以准确地预测公路边坡稳定性。

针对以上分析，本文综合利用主成分分析法[9-10](Principle Component Analysis，PCA)的特征提取能力，LM 算法[11-12](Levenberg-Marquardt)全局寻优的能力，以及BP 神经网络方法[13-14]较强的非线性映射能力和自适应能力的特点，以辽宁省阜新市中南公路的岩质边坡工程为例[15]，建立了基于PCA-LM-BP 神经网络的公路边坡稳定性预测模型，为公路边坡稳定性预测提供了一种新方法。

1 模型简介

PCA[16-17]是一种有效的降维手段，其目的就是在原始变量损失较少的情况下，重新线性组合出一组线性无关变量代替原来具有一定相关性的变量。

LM 算法是[18-19]梯度下降法和高斯-牛顿法的结合， 同时具有梯度下降法的保证收敛特性和高斯-牛顿法的快速收敛特性。

BP 神经网络[20-21]由一个输入层、一个或多个隐含层、一个输出层组成，各层次的神经元之间单向全互联连接，是一种由非线性变换单元组成的前馈型网络。

2 预测模型的建立

2.1 公路边破稳定性评价指标的确定

以文献[15]中的辽宁省阜新市中南公路边坡稳定性实测数据为例，选取重度(kN·m-3)、内聚力(MPa)、摩擦角(°)、边坡角(°)、边坡高度(m)、日降水量(mm)这6 个因素作为影响中南公路边坡稳定性的评价指标，评价结果为边坡状态是否发生破坏。 将样本数据归一化处理后从23 组数据中随机选取18 组数据作为学习样本(表1)，剩下的5 组作为预测样本(表2)。 表中“1”表示边坡稳定，“-1”表示边坡破坏。

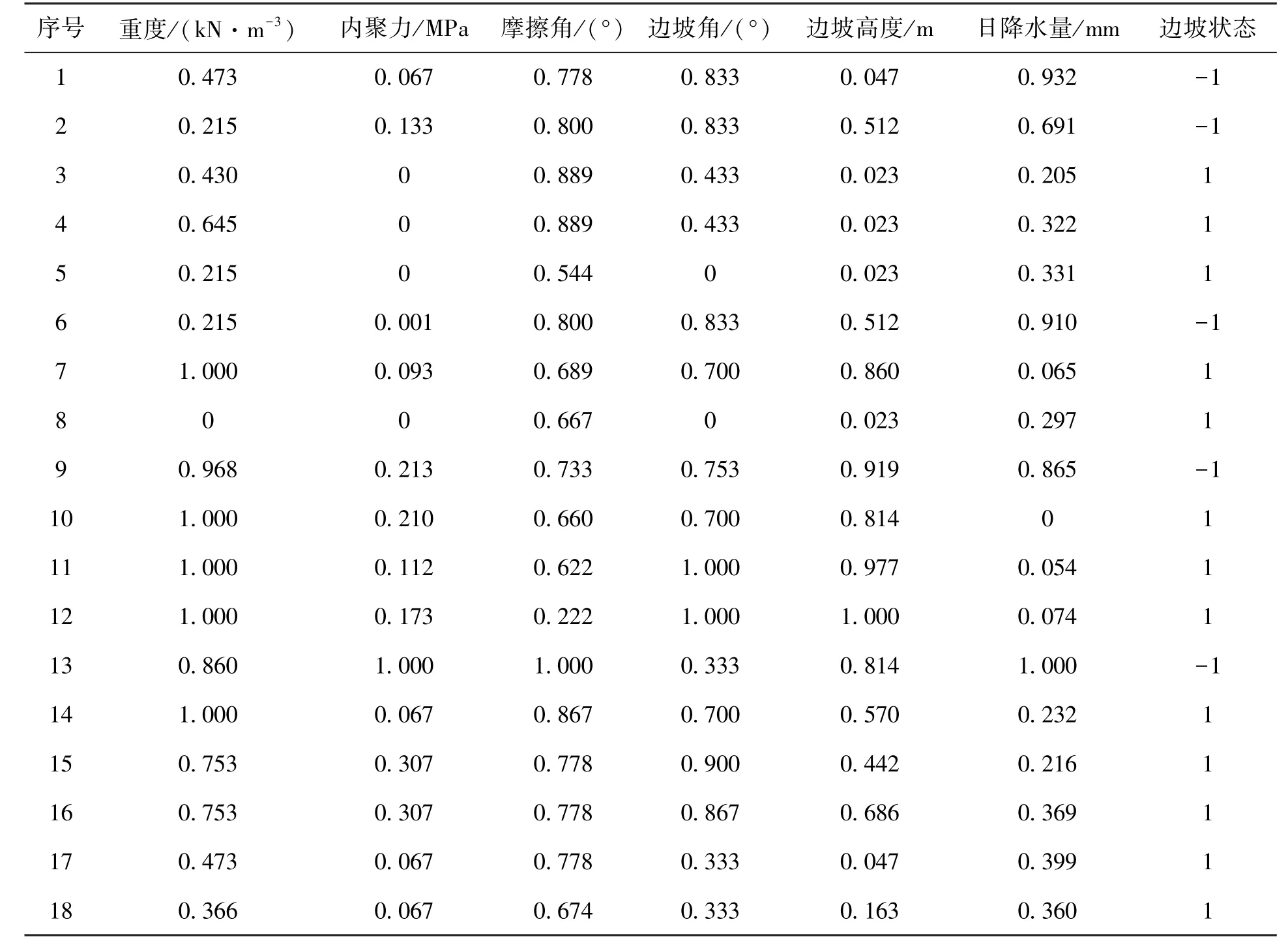
表1 学习样本归一化处理Tab.1 Normalization of learning samples

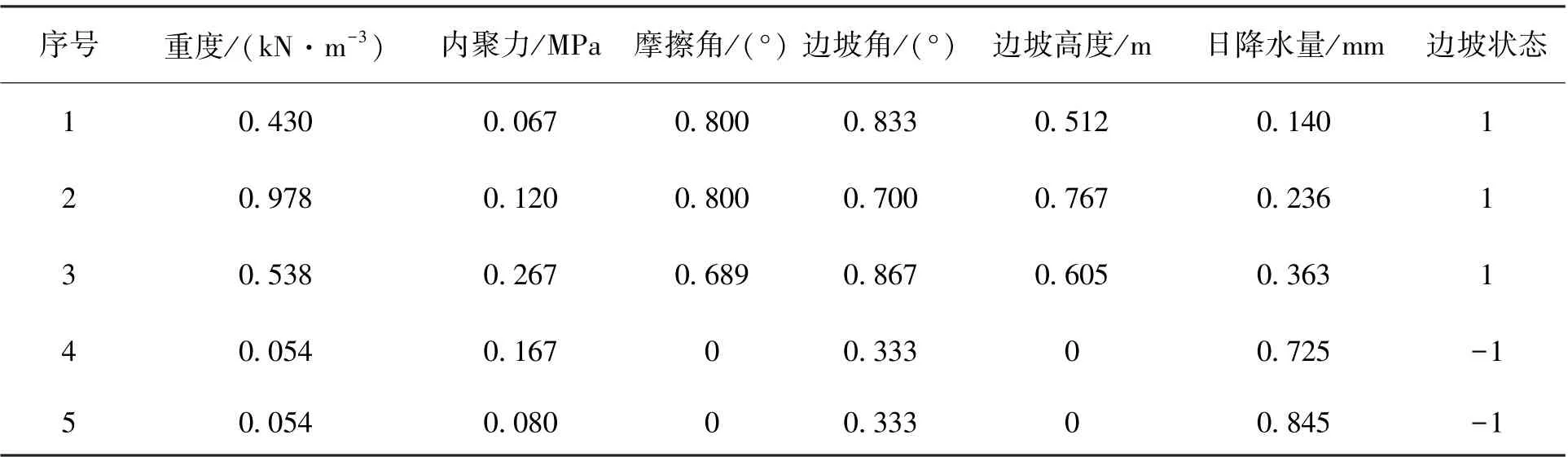
表2 预测样本归一化处理Tab.2 Normalization of prediction samples

2.2 公路边破稳定性评价指标的主成分分析

表3 为对表1 和表2 中的6 个影响因素进行主成分分析得到的相关系数矩阵，由表3 可知，重度与边坡角、边坡高度有较强相关性；内聚力与边坡高度有较强相关性；摩擦角与日降水量有较强相关性。 若直接对这些影响因素进行分析，可能会出现共线性的问题，影响后续模型的预测精度。

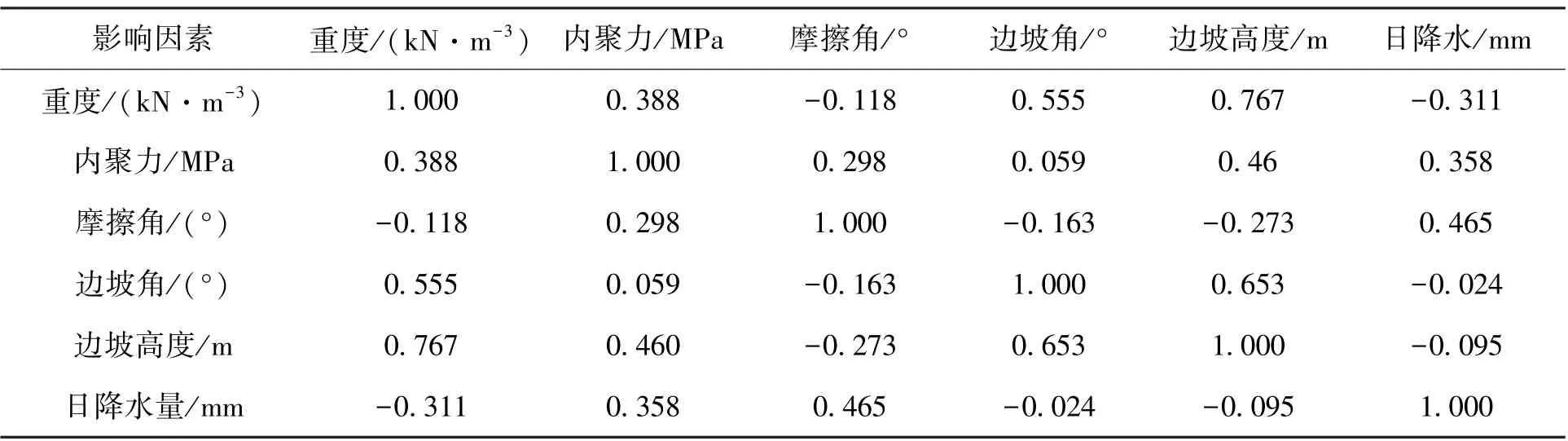
表3 相关系数矩阵Tab.3 Correlation coefficient matrix

表4 为6 个影响因素的公因子方差比。 由表4 可知，除了重度和边坡高度有8.3%的信息未被提取外，其他4 个影响因素的信息被提取得较为充分。

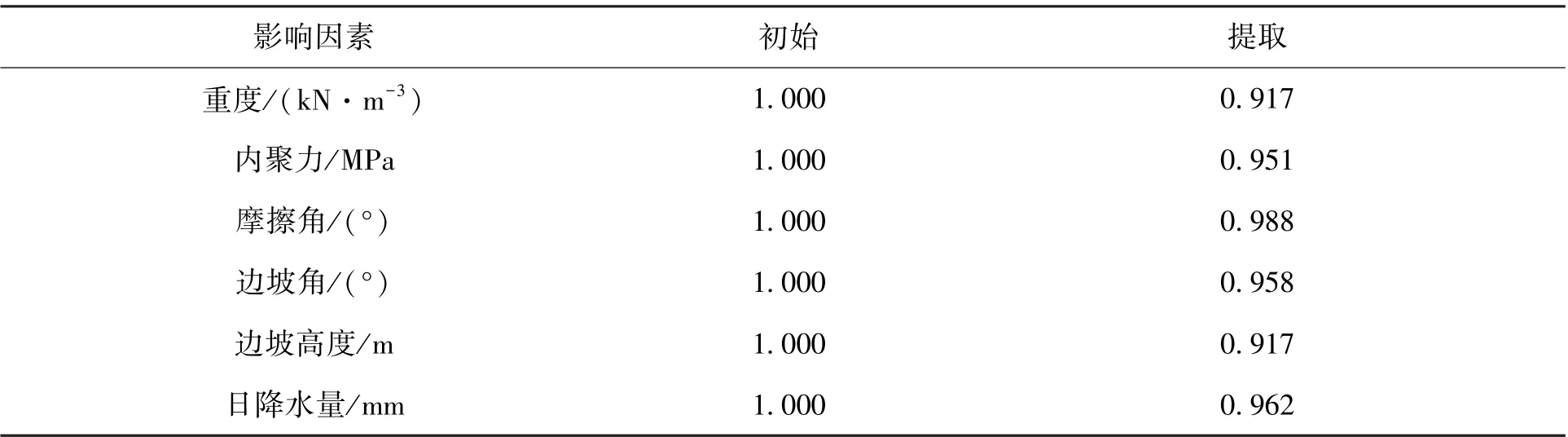
表4 公因子方差比Tab.4 Variance ratio of common factors

表5 为对6 个影响因素进行主成分分析得到的各主成分特征值及贡献率。 由表5 可知，前4个主成分的累积贡献率为94.881%＞85%。 结合图1 可知，从第4 个主成分开始，后面主成分的特征值较低，因此取前4 个主成分代替原始6 个影响因素的信息量。

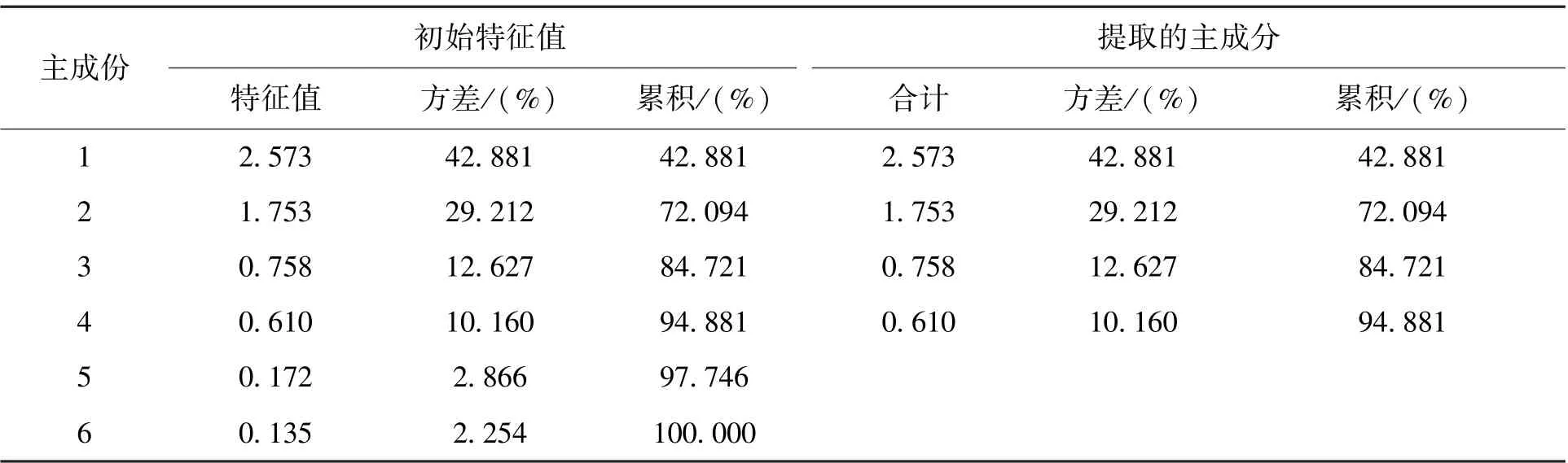
表5 主成分特征值及贡献率Tab.5 Characteristic value and contribution rate of main components

表6 为通过主成分分析得到的因子得分系数矩阵，提取的4 个主成分为原始数据通过该系数矩阵重新线性组合的结果，4 个主成分的表达式见式(1)。 其中，S1、S2、S3、S4分别表示第1 主成分、第2 主成分、第3 主成分和第4 主成分， x1、x2、x3、x4、x5、x6分别表示重度(kN·m-3)、内聚力(MPa)、摩擦角(°)、边坡角(°)、边坡高度(m)、日降水量(mm)。

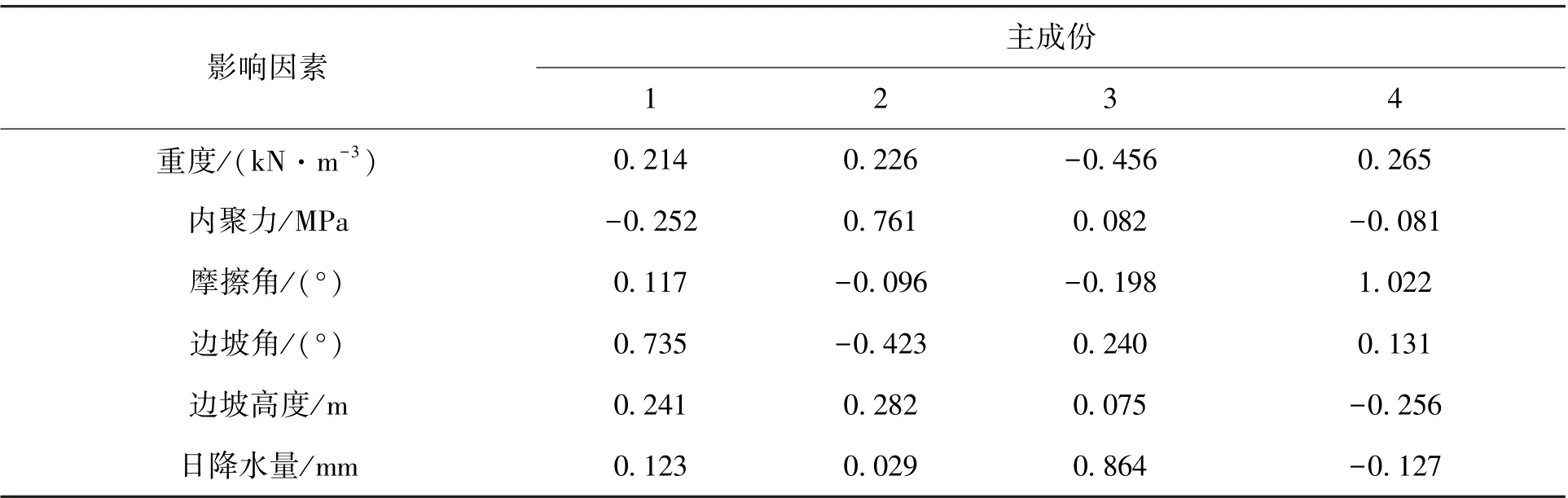
表6 因子得分系数矩阵Tab.6 Factor score coefficient matrix

通过主成分分析法对学习样本和预测样本进行分析，将提取的4 个主成分( S1、S2、S3、S4)代替原来的6 个影响因素，作为BP 神经网络模型的输入变量，既解决了影响因素间的共线性问题，也提高了预测模型的运算效率。

2.3 模型的建立

通过主成分分析后，以式(1)确定的4 个主成分( S1、S2、S3、S4)作为输入变量，用LM 算法优化的BP 神经网络模型对学习样本进行回归仿真训练，对学习样本的预测结果与实际结果进行对比，如图3 所示。 由图3 可以看出，预测结果与实际结果较为接近，预测精度能够满足实际工作的要求。

2.4 预测结果与分析

基于PCA-LM-BP 神经网络模型对表2 的预测样本进行预测，并与原始数据的实际结果进行对比，如图4 所示。 该模型预测结果误差与LMBP 神经网络模型、BP 神经网络模型预测结果误差进行对比见表7。

结合图4 和表7 可以看出，基于PCA-LM-BP神经网络的中南公路边坡稳定性预测模型的最大误差为0.041，最大相对误差为4.10%，而LM-BP神经网络模型最大误差为0.063，最大相对误差为6.30%；BP 神经网络模型最大误差为0.102，最大相对误差为10.20%。 通过对比三种模型的预测结果可以看出，基于PCA-LM-BP 神经网络模型能够较为准确地预测中南公路边坡稳定性的状态，在精度上优于LM-BP 神经网络模型和BP神经网络模型。

表7 三种模型误差对比Tab.7 Comparison of errors of three models

3 结论

本文综合利用主成分分析法对影响公路岩质边坡稳定性的6 个因素进行主成分提取，并建立了基于PCA-LM-BP 神经网络的公路边坡稳定预测模型，得到如下结论:

(1)中南公路岩质边坡稳定性的状态受多个因素共同影响，常规简单的数学模型较难反映因素间的非线性关系，本文采用主成分分析法较好地解释了影响因素间的复杂关系。

(2)利用基于PCA-LM-BP 神经网络的边坡稳定性预测模型，对中南公路地区23 组实测数据进行训练并预测，结果显示23 组公路边坡样本中，边坡状态为破坏的7 个，边坡状态为稳定的16 个，该结果与当地实测结果较吻合。

(3)基于PCA-LM-BP 神经网络的中南公路边坡稳定性预测模型的建立，为分析和研究公路边坡稳定性提供了一种新思路，该模型预测精度高，具有一定的可行性。