基于改进滑模控制的动车组网侧PWM整流器

郭志强 张新燕 高亮 童涛,2 张家军

（1.新疆大学 新疆维吾尔自治区乌鲁木齐市 830047 2.中国航空工业集团第六三一研究所 陕西省西安市 710065）

1 研究背景及意义

近年来，随着国民经济快速发展对铁路运输的需要及国家战略需求，在2016年至2025年（远期至2030年）期间规划建设以八条纵线和八条横线主干通道为骨架、区域连接线衔接、城际铁路为补充的高速铁路网。中国铁路朝着更多、更快、更好的方向发展。一方面，中国高速铁路营业总里程达到3.5万公里，位居世界第一（截止2019年底）；另一方面，既有铁路线迎来了第六次大规模提速[1]。我国动车组从引进、消化吸收，再到自主研发，经历非同寻常的技术变革。目前在中国交-直-交动车组大批量的投入运营，牵引供电系统的多样性也在不断增加。PWM 整流器作为动车组网侧变流器通过牵引变压器与供电网撮合，其整流器网侧电流中的谐波将注入供电网[2]，给电网造成谐波污染。该谐波畸变电流通常包括低次谐波和高次谐波；低次谐波成分一般较大，会造成较为严重的网压畸变，对运行于同一供电线路上的其他列车可靠运行造成威胁。传统动车组网侧PWM 整流器一般采用传统PI 控制，动车组网侧PWM 整流器采用的是双闭环PI 控制，通常在理想情况下，在参数匹配的情况下整流器能够具有较好的性能，一旦系统参数发生变化，出现了内部或者外部的干扰，由于其极点不能任意配置，将会导致整流器的性能就会降低，鲁棒性降低。主要表现为动态响应慢，网侧电流谐波畸变率较大，其次直流侧电压波形波动较大。现有研究表明车网稳定性主要是由PWM 整流器控制决定的[3]所以整流器控制性能的提升，谐波治理问题，受到广大学者的关注，对其控制策略的研究以及控制性能的改善与提高具有现实意义。

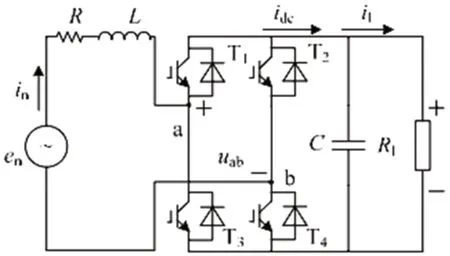
图1：动车组网侧PWM 整流器拓扑结构

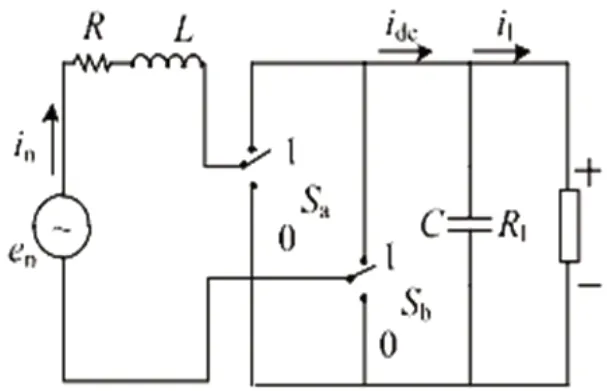
图2：动车组网侧整流器等效拓扑结构

文献[4]为了改善PI 调节的滞后性及三相电压型 PWM 整流器的非线性特征，使得 PWM 整流器在扰动下获得良好的动态性能，首先建立PWM 整流器在两相同步旋转坐标系下的数学模型，设计了一种适用的变结构控制算法，当系统出现干扰，以及系统参数发生变化时，基于滑模变结构控制算法下的系统，具有很强的鲁棒性。在 Matlab /Simulink 环境下搭建了PWM 整流器控制系统仿真模型，验证了滑模变结构控制算法具有更好的动态性能。文献[5]详细介绍了滑模变结构的参数设计，以及可选择功能的滑模控制器的分析。在 Matlab/Simulink 中搭建全二阶解耦双闭环仿真模型，分析双闭环控制系统的响应时间和抗干扰性能，并与三相电压型 PWM 整流器的传统 PI 控制进行比较。仿真结果表明，基于滑模控制的方法是有效的，提高系统动态性能，改善了系统的稳定性。文献[6]针对传统PI 控制器在负载突变，电流内环参考指令跟踪调节速度慢、存在静态误差等问题，提出基于电流内环的优化比例谐振（Proportional Resonant，PR）控制器，并结合具有开关特性的滑模控制器，以此来降低PI 控制的电压外环控制器，对电流内环控制精度的影响。最后，搭建实物平台，对所提方法进行验证，实验结果表明滑模PR 控制策略的可行性和有效性，且具有较好的工程实际应用价值。文献[7]通过对滑模变结构和内模控制理论的研究，设计出电压外环滑模变结构控制器和电流内环内模控制器。搭建三相可控整流器的实验电路，采用滑模变结构及内模控制算法进行整流器满载、半载及半载转满载实验，验证元器件参数计算及选型合理性以及系统软硬件设计的可行性。实验及仿真结果表明，基于滑模变结构及内模控制的三相可控整流器，具有良好动静态性能且交流侧谐波畸变率低，能够实现单位功率运行，对电网污染小。文献[8]设计出基于滑模变结构控制的三相整流器双闭环控制方案。在理论研究的基础上，釆用对设计方案进行仿真实验，与传统的控制方案进行比较及分析。实验结果表明该系统能够实现快速响应并在最短的时间内达到稳定值。文献[9]针对三相 PWM 整流器提出一种新型滑模控制策略，建立控制模型，与传统双闭环 PI 控制算法进行对比分析，结果表明所提方法增强了控制系统的鲁棒性。文献[10]将采用滑模控制成功的抑制了牵引网低频振荡现象，但直流侧电压波动较大，谐波分散。可见滑模变结构控制能够很好的应用于各种领域和PWM 整流器当中，并且提高了被控系统的动静态特性，具有较强的鲁棒性。

综上所述本文考虑将滑模控制策略运用的动车组网侧PWM 整流器当中，以此来改善整流器控制性能。

2 动车组网侧PWM整流器模型

本文以动车组网侧去除LC 滤波装置的单相电压型PWM 整流器作为研究对象，其拓扑结构图如1 所示。图1 中：L 和R 分别为车载变压器等效到次边的漏电感和漏电阻；C 为直流侧支撑电容；Rl 为负载等效电阻；Udc 为中间直流侧负载电压；uab为上图a 与b之间的电压值，即动车组网侧整流器输入电压；en为网侧电动势；in为网侧电流；il为负载电流；idc为il与电容C 的电流之和；T1～T4为绝缘栅双极型晶体管与二极管并联形成的桥臂。根据其拓扑结构，得到下列状态空间方程：

对整流器工作状态分析可知，上下桥臂的开关信号必须互反，所以理想开关函数只存在 1、0 两种状态，因此定义了理想开关函数Sa 、Sb 如下：

整流器等效结构图如图2 所示。

理想开关下的等效拓扑结构，开关状态一般有四种状态，分别为SaSb=00、01、10、11。其中SaSb=00、11 时，uab取值为0。不同的情况：udc、0、-udc。在实际工作中， 动车组网侧PWM 整流器，在控制系统的作用下，对上述三种不同工作模式的选择，以此来控制开关管的通断，实现能量的双向流动和输出电压稳定。通过对单相脉冲整流器不同工作模式的分析，根据上面所定义的开关函数，动车组网侧 PWM 整流器输入端电压如下式所示：

由于整流器电气量之间存在耦合关系，因此在应用滑模变结构控制策略前，需要对整流器相互存在耦合的电气量进行解耦。针对被控制系统，需要在原有变量的基础上，构建一个in的虚拟正交信号iβ，并将表示为in，得到单相交流信号在两相静止坐标系的分量，其他电气量则与in同理。再通过式（4）的坐标变换，实现交流信号到直流信号的转换。

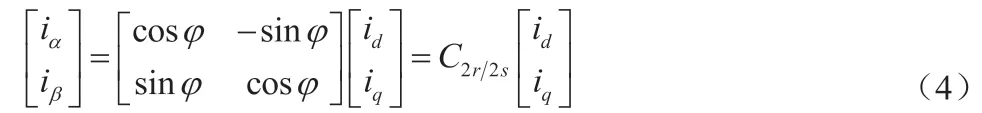
对式（1）进行式（4）的坐标变换，得到：

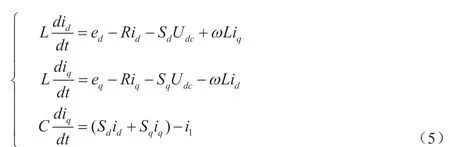
式中ed、eq为eα、eβ转换到两相旋转坐标系下的有功无功解耦分量。式（5）为动车组网侧整流器在两相旋转坐标系下的数学模型。

3 整流器滑模控制器设计

首先滑模控制的实现是建立在滑动模态存在的基础之上的。按照滑动模态区上的运动点都必须是终止点这一要求，当运动点到达切换面s(x)=0 附近时,必有：

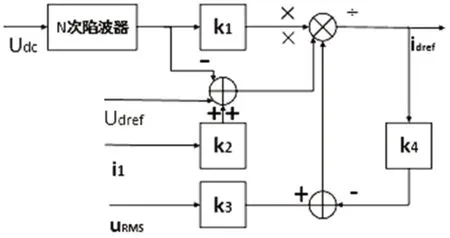
图3：加入N 次陷波器电压环控制结构图

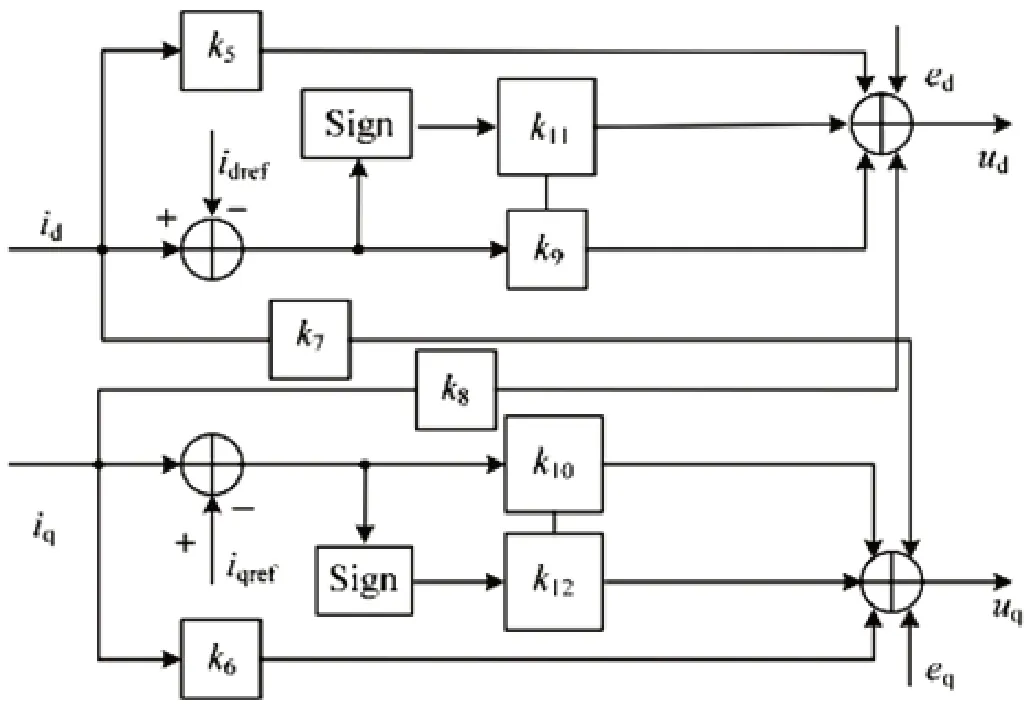
图4：采用Sign 函数的电流内环控制结构图

上式s 与 符号相反。滑模控制器设计主要分为两步：首先选取合适的切换函数；其次，选取合适的控制率。PWM 整流器控制目标为Udc和iq：维持直流侧的电压Udc相对稳定；其次，功率因数为1，即无功功率为接近0，理想情况下使得iq=0。

3.1 外环电压控制率求取

电压环控制器的结构如图3 所示。由于直流侧二次纹波会诱发网侧电流中产生3 次电流谐波，牵引网压或网流中的3 次谐波又会导致直流侧电压中出现四次纹波。为此，根据PWM 整流器控制系统的特点，由图3 所示：选取陷波中也频率为2、4、6 倍电网电压频率的3 组陷波器，并将其串联后加于直流电压反馈通道，来消除反馈信号中的2、4、6 次电压纹波，并实现电压外环输出控制量恒定的目的。在电压反馈通道中采用N 次陷波滤波器，具有动态响应快和易数字化实现的优点。直流侧电压 Udc 与负载电流il 由传感器获得；Udc的参考为值Udcref；uRMS为网侧电压有效值；k1、k2、k4为与动车组网侧整流器参数有关的常数，k3为2。

基于滑模控制的电压环控制器的一般设计方法如下：首先，根据动车组网侧整流器的控制目标选择Udc、iq为控制系统的输出。设分别表示的误差值：

其次，建立滑模面s1、s2：

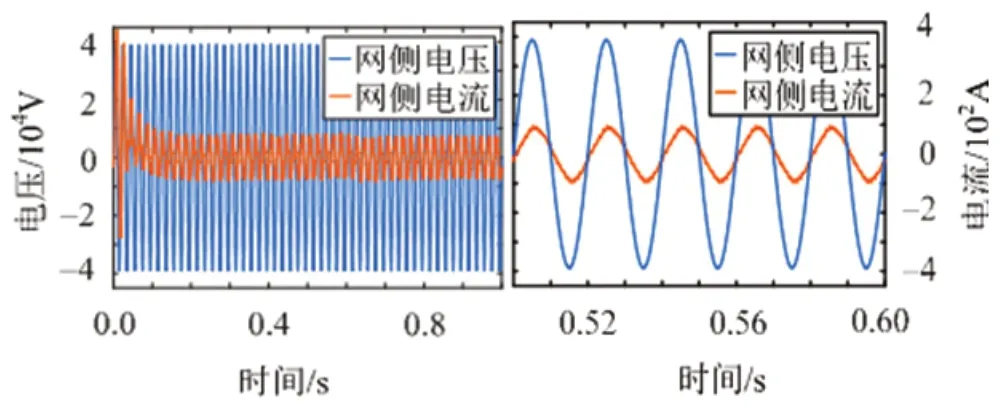
图5：基于滑模控制的牵引网电压电流波形

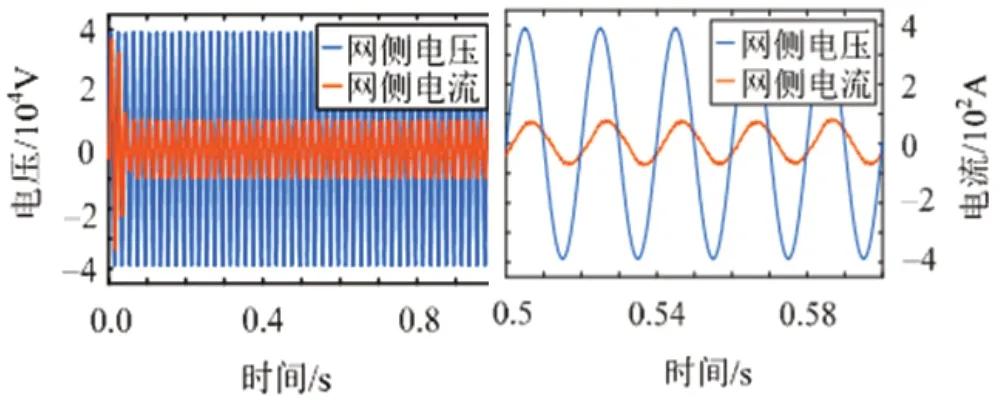
图6：基于 PI 控制的牵引网电压电流波形

式中 α、α1、α2为增益。将滑模面s2的表达式中的用β 代替，得到id的表达式：

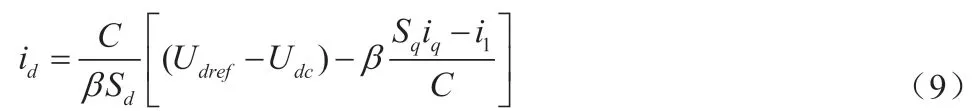
将式（10）带入式（9）可得：

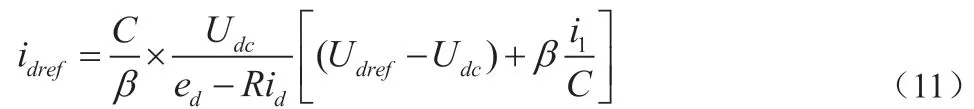
式（11）为搭建电压控制模块提供了理论依据。

3.2 内环电流控制率求取

电流环控制器的结构如图4所示。ed、eq为网侧电压 d、q 轴分量；有功电流参考值idref为电压环控制器的输出；设置无功电流参考值iqref 为 0 来达到功率因数接近1 的控制目标；k5-k12均为与系统参数有关的常数。

sgn 模块为符号函数：

为使系统同时具有较好的动态性能与稳态性能，选择指数趋近率，指数趋近率的形式为s·=-ε sgn(s) -ks(ε>0, k>0)，由于Signum函数本身是不连续的，进而影响系统的稳定性，造成直流侧输出电压在达到稳态后电压的波动幅值较大。为了减小抖振，本文采用连续的Sigmoid 函数代替Signum 函数来减少抖振，进而改善输出电压波形的波动。Sigmoid 函数定义为：

式中a 为大于0 的可调参数。取两个滑模面，采取指数趋近律的形式，可得：

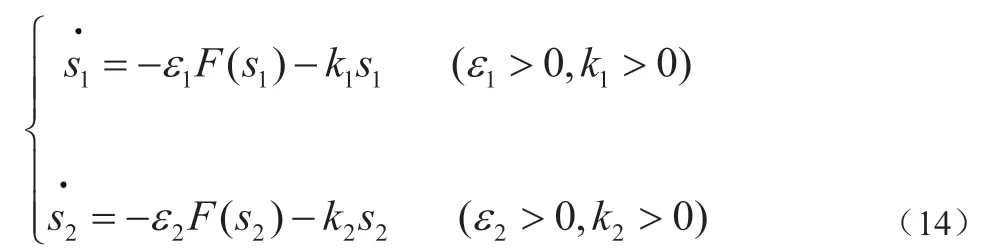
将式（7）代入上式，得到：

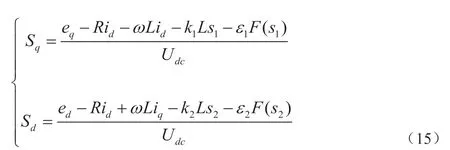
最后，将式（15）进行坐标变换可得到脉冲调制波信号，直接输入脉冲调制模块。

4 仿真分析

在MATLAB/simulink 搭建基于滑模控制的动车组网侧PWM整流器仿真模型，与传统PI 控制的动车组网侧PWM 整流器进行对比仿真分析。牵引网网压有效值为27500V；给定直流侧电压为3600V；车载变压器漏电阻为0.145Ω；直流侧负载等效电阻25Ω；车载变压器漏电感为0.0054Н；直流侧支撑电容为0.009F；仿真步长为5×10-5s；采样频率为10kНZ，调制方式采用SPWM 正弦脉宽调制。首先从四个方面对针对两种控制方式下的PWM 整流器直流侧电压控制效果进行对比分析，具体指标包括超调量、峰值时间、调节时间、电压波动。然后利用MATLAB/simulink 当中power gui里的工具FFT Analysis 分析了两种控制方式下网侧电流的畸变率。考虑注入3、5、7 次谐波。以此来检验检验整流器的抗网压畸变能力。

由图5 和6 所示：左侧为¬0-1s 内电压电流的波形，右侧为稳定后，0-0.6s 电压电流的波形，可以看出两种控制方式下的波形接近正弦波，且比较平滑，电压电流无明显畸变，PI 控制下的电流峰值超过了400A，而滑模控制下的电流峰值小于400A。

图7 与图8 为基于滑模控制与PI 控制的直流侧电压波形。由图7 和图8 可以看出，在动态响应速度方面，滑模控制是明显优于PI 控制，滑模控制在0.1s 内实现稳定，而PI 控制接近0.8 秒才实现稳定；PI 控制是有

超调量的，而滑模控制无超调量。达到稳态后，PI 控制下的电压波动为70V，优化滑模控制下的直流侧电压波动仅为40V。

在实际工作环境当中电网是含有谐波的，一般含有低次谐波。所以本文考虑在网侧注入10%的3、5、7 次谐波，来检验两种控制方式下的网侧电流畸变率。4-13 和图4-14 为当牵引网侧注入3、5、7 次谐波时，通过对网侧电流FFT 分析。由图9 和图10 可以看出：当电网网压发生畸变时，基于滑模控制的网侧电流畸变率为2.3%，PI 控制的网侧电流畸变率为4.54%。基于滑模控制的整流器具有更小的网侧电流畸变率。

图7：基于优化滑模控制的直流侧电压波形

图8：PI 控制的直流侧电压波形

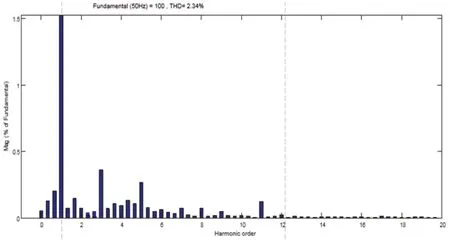
图9：基于滑模控制的网侧电流FFT 分析

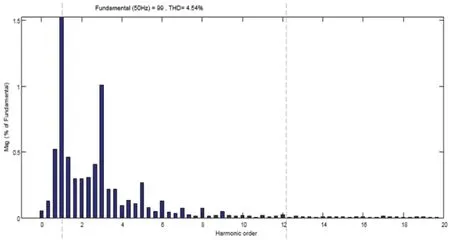
图10：基于PI 控制的网侧电流FFT 分析

5 结论

针对传统PI 控制动态响应速度慢，本文考虑引入高鲁棒性的滑模变结构控制策略，针对网侧电流畸变率大的问题，本文在传统滑模控制策略的基础上加以改进，在直流侧电压反馈控制环节加入了陷波器来抑制直流侧的脉动。依据滑模控制器设计的基本步骤，针对本文所研究的对象以及控制目标，设计出了适用于整流器的滑模控制器，针对滑模控制的抖振问题，采用连续的Sigmoid 函数来代替滑动模态当中的不连续的Signum 切换函数函数，以此来降低滑模控制固有的抖振。通过仿真分析，验证了本文所提方法的有效性。