民航旅客后续行程推断方法应用

邹威

（北京交通大学计算机与信息技术学院 北京市 100044）

1 概述

伴随着近些年民航业的飞速发展，以及人民消费水平的不断提高，旅客出行方式、服务流程和交互方式正在不断演变，旅客开始追求更加品质化、个性化的消费需求，越来越多的人选择更加高速便捷的航空出行方式以节省时间。2019年3月5日，民航局发布《2018年民航机场生产统计公报》[1]，数据显示，2018年我国境内机场主要生产指标保持平稳较快增长，全年旅客吞吐量高达12.64 亿人次，较2017年增长10.2%。随着机场旅客吞吐量的不断增加，旅客对服务质量的要求也越来越高，除此之外，旅客的出行模式也发生着变化，不局限于传统的往返模式，因此旅客的订票行为模式也在改变，这也给民航业提出了新的挑战。如果我们从一个旅客出行全流程的时间段分布出发，大致可以分为出行前、在途、出行后。而在出行前与在途这两个阶段中，存在这么一类旅客，我们称为“行程未预定完成旅客”（后均简称为“旅客”），指还未预定好当前完整航程的全部机票的旅客。而据中国航信数据统计表明，在2018年的旅客出行记录中，约33%的旅客不会一次性预定完完整航程的全部机票，这些旅客短时间内还会形成新的或临时的订票需求，但这些潜在的需求未能得到及时的满足。由于现阶段我国民航市场每年近十几亿人次的出行总量，所以这些具有迫切需求的旅客则是需要被服务的重点。如果能对这些旅客的后续行程进行较为准确的预测，这将会帮助各大航空公司和机票代理商提供更加有的放矢的机票推荐服务，还会给旅客带来更好的消费体验，甚至提高整个民航业经济效益。因此，在本文中，我们将尝试对这个与实际业务场景紧密联系的应用问题进行分析，实现对旅客后续行程预测方法的整体应用方法研究。

截止到目前为止，关于民航领域旅客行程推荐方面的研究主要是以单个旅行产品的推荐为主，缺乏对特定场景和特定旅客的后续行程预测，还无法及时满足对旅客精准化和个性化的出行需求。同时民航旅客个体出行数据间隔更为稀疏，不规则变动较大，也同时容易受到时间、天气等外界因素影响。因此，旅客后续行程预测的研究对民航领域的旅客智能化发展来说是非常必要且充满挑战的。

2 相关研究

近些年来，国内外学者在民航旅客出行预测领域也进行了相关的研究，其中一部分研究主要是对旅行产品的相关推荐服务[2]，比如，Lim K Н 等人基于用户兴趣和兴趣点[3]，来推荐航空旅行产品服务；JIE LIU 等人通过旅客关系网络和提出的个性化出行主题概率图模型[4]，为旅客推荐未来潜在的出行路线。而如果我们将旅客的出行记录按照时间顺序进行序列化研究，目前在序列预测领域也已经有了很多的研究，尤其是电商领域热门的点击率预测[5][6]也在序列预测上取得了不错的效果，比如，Balázs Нidasi 等人首先提出的考虑用户行为的时间偏移的循环神经网络模型进行点击序列预测[7]，Jing Li 等人提出了一种新的NARM 模型[8]，该模型考虑了用户在当前会话中的顺序行为和主要目的，并使用双线性匹配方案计算推荐分数；Liu, Q 等人通过运MLP 模型与注意力网来捕获用户的一般兴趣和当前兴趣[9]。在民航旅行产品的相关研究中，这些方法都是只考虑了旅客历史行程，进行潜在的民航旅游产品推荐，并没有参考旅客当前所处的完整航程状态，并没有做到针对每个特定旅客的个性化预测和推荐。而在系列预测的相关研究中，现有的这些方法在处理序列点击预测方面，确实有着不错的效果，但面对民航旅客特有的出行模式多样化、出行数据稀疏和出行间隔不规则等特点，还无法准确预测出旅客的后续出行目的地，尤其是对于一些相对较长的序列的预测效果上对比短序列还是有一些差距。

可以说，目前并没有太多直接应用于解决民航旅客后续行程预测的研究，为了解决上述问题难点，我们结合民航旅客出行数据的特点，对其他领域内关于序列预测的主要研究进行了分析，发现在电商推荐领域中的网站点击率预测方法中，一种基于图结构模型的推荐系统能够很好的学习用户与商品之间的强交互关系，并实现高度准确的商品推荐[10]。因此，本文将这一图结构模型类比应用到本文的问题中，首先通过图神经网络[11]对旅客的历史出行城市序列进行建模，构建对应的有向图，并额外引入全局航线网络，获取融合了邻居信息的城市节点表示，然后引入注意力机制同时考虑旅客的历史出行兴趣与当前所在城市的重要性，实现对旅客的后续行程预测。本文在长期大量的民航旅客出行数据集上进行多组实验，结果验证了基于图神经网络结构的预测模型效果的显著性。

3 问题定义与方法分析

3.1 问题定义

本文要解决的预测任务是，针对于行程未预定完成旅客，根据一定时间内的历史出行城市序列，预测其下一次出行的候选目的地集合。对于任意旅客，其历史行程记录可以表示为，其中hi表示旅客行程记录中下标为i 所对应的城市，n 为该旅客行程记录长度，hn为该旅客当前所在的城市。由于最终是为了预测旅客下一次出行目的地，该目的地可以是与旅客当前所在城市之间有航线的全国任意一个城市，我们称之为候选城市集合，即可以表示为city_set=，其中K 表示该候选城市数目。我们通过输入旅客历史前M 条记录序列来预测第M+1 位置的城市hM+1，即通过输出候选城市作为旅客下一个目的地的概率分布并选择概率最大的前k 个城市作为最终的预测结果集合。

3.2 方法分析

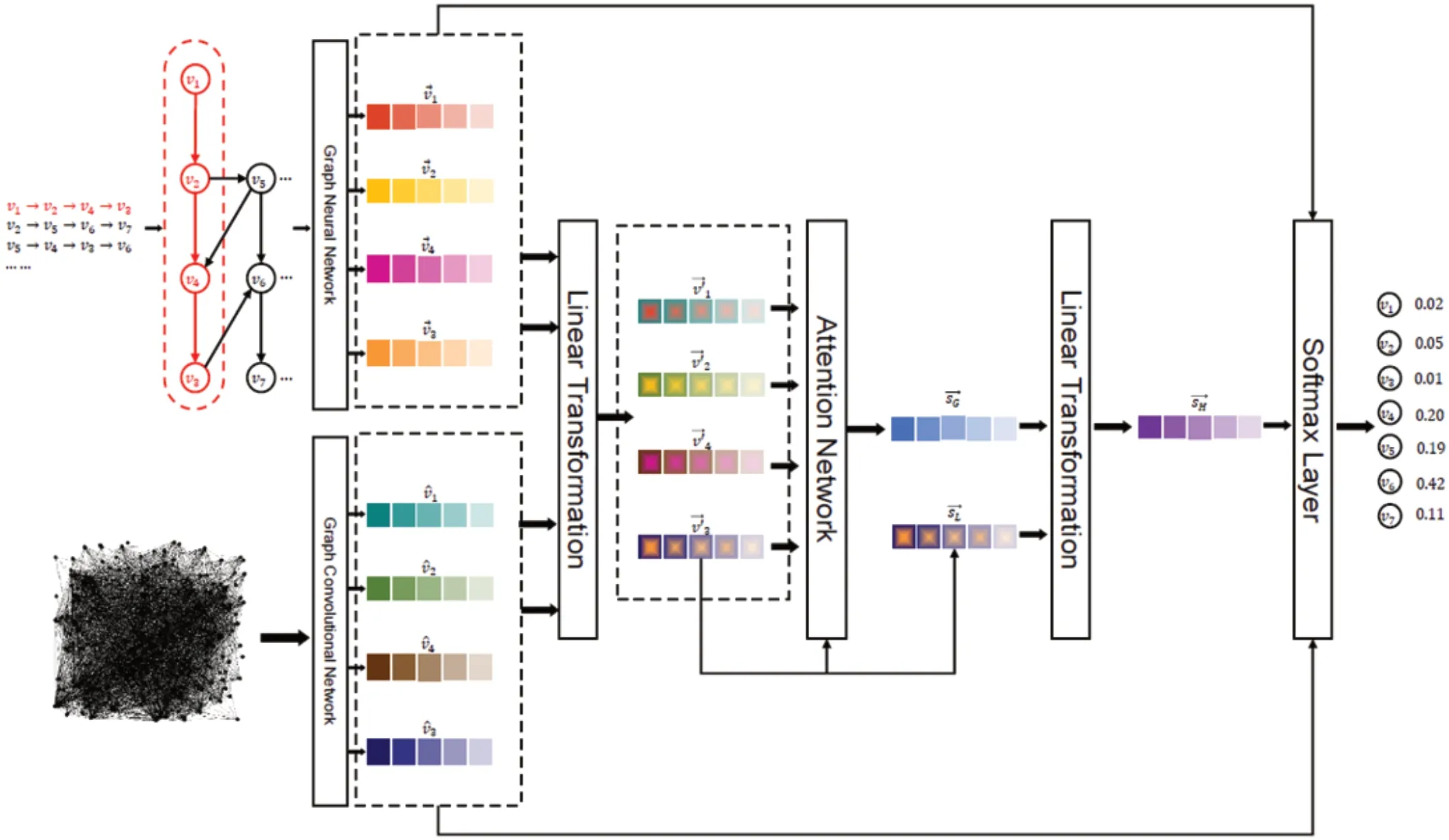
图1：模型结构图

本文采用的是一种基于图神经网络、注意力机制和全局航线网络的后续行程预测模型的架构图如图1 所示。首先，我们获取旅客的历史前M 条出行记录序列来预测第M+1 位置的城市，通过图神经网络建模，得到每个出行城市的节点向量表示。然后，同时考虑旅客的历史出行兴趣和当前所在城市的重要性，通过引入注意力机制，基于其他历史出行城市节点向量与当前城市节点向量两两计算相似度，作为本次出行输入的全局向量的表示，并将当前城市向量作为局部向量表示，将两者融合成为新的出行序列向量表示。最后，将这个最终得到的出行序列向量通过一个softmax 层计算出下一次出行的城市的概率分布，取排名最高的前k 个城市最为最终的预测城市集合。

3.2.1 全局航线网络与城市节点嵌入

为了更好的对候选城市集合进行预测，我们认为预测的城市集合要与当前城市之间有航线，所以我们先根据民航旅客的历史出行记录进行汇总计算，构造出一个全局航线网络(G,V,E)。其中每个出现的城市作为一个节点，城市之前有航线可达则节点之间有边。模型先基于航线网络(G,V,E)通过图卷积网络获得每个节点的全局结构信息表示

对于每个旅客的出行城市序列集合，我们输入其前N-1 个城市所构成的出行城市序列输入到模型中，先生成相应的有向图(G',V',E')（其中V'为有向图节点集合，E'为有向图边集，一般的|V'|≤N-1）。通过一个映射函数{f:Н →V}将hi映射成与之相对应的有向图节点vi，于是序列中每一个hi均通过函数f映射到对应的节点vi并赋予与该节点所对应的向量作为城市初始表示并获取该城市id 序列对应的全局结构信息

在序列中的每个城市节点嵌入表示的过程中，对于图G'的一个节点嵌入vi，它在t 时刻的更新函数如下：

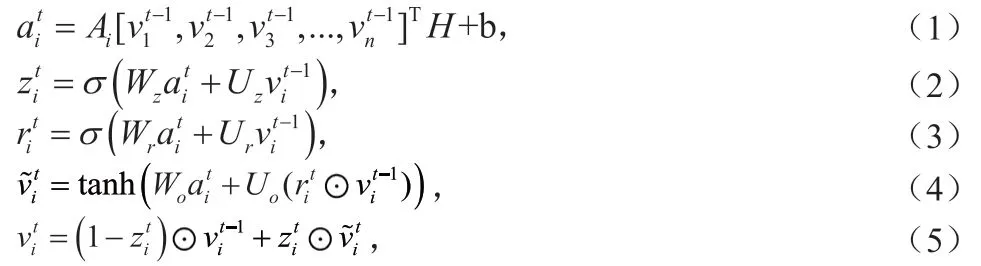
3.2.2 出行序列表示

在获得旅客出行序列的每个城市的表示之后，我们需要重新对旅客的出行序列进行向量融合，由于我们认为旅客的后续出行目的地除了受到其历史出行规律的影响之外，还主要受到其当前所在城市的影响，后续出行城市与当前城市的航线网络关系以及历史出行频次都将影响结果。

所以模型还将引入注意力机制，将其他城市节点向量与当前所在城市节点向量进行两两计算相似度，作为生成本次输入全局向量的权重偏好，考虑当前所在城市的重要性，将其作为局部向量表示，并与基于注意力机制生成全局向量融合，通过一个全连接层，最终输出作为该历史出行向量表示

3.2.3 计算出行概率分布

我们将最后得到的这个旅客历史出行向量经过一个softmax 层，最终输出候选集合中每个城市被选中的概率分布，并与该样本的真实标签计算交叉熵：

其中p 为候选集中每个样本被选中的真实概率分布，q 表示模型预测的候选集中每个城市的概率分布，M 为候选城市集。通过计算损失函数：

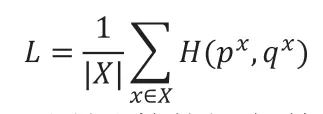
对所计算的损失利用后向传播算法经过多轮迭代并更新模型中参数以更好的拟合真实样本分布。

4 实验与结果分析

4.1 实验数据与实验参数

为了还原真实旅客出行的情景，本文使用了2015年1月1日至2018年6月30日脱敏匿名化后的真实旅客出行记录，共涉及旅客量10 万人，完整航程记录264647 条，航段数量470239 条。

然后基于如下策略进行数据集划分：首先在原始数据集的基础上根据旅客历史总航段数目筛选历史总航段数不低于3，5,10 的旅客记录，将其划分为origin@3,origin@5,origin@10 三个数据集，并分别进行训练集和测试集的划分，如表1 所示。

本实验中我们采用top_5 作为推荐城市集合数量，在模型训练阶段，整个数据集训练轮次的最大次数为20，学习率取1e-3，学习率衰减参数取0.5，学习率衰减轮数取10，训练集与预测集的批次取128。

4.2 实验评估

为了进行实验评估，我们将图结构预测模型与目前已有的几种序列预测方法进行比较：（1）GRU 模型；（2）STAMP 模型；（3）FF 模型（frequency_first），即对旅客历史所到达城市按照频率从大到小排序，对前top_k 个城市作为最终的推荐集合。

实验所使用评价指标包括hr@k 和mrr@k，其中k 表示前k 个城市所构成的推荐城市集大小，具体如下所示：

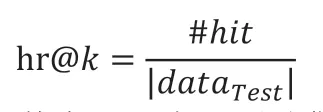
其中#hit 表示测试集中预测命中的个数，其中我们认为旅客真实到达的目的地h_N 出现在大小为k 的推荐集合中则表示该次预测命中。

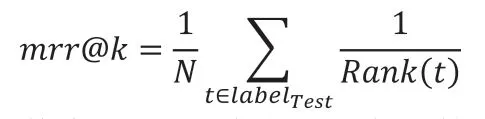
其中Rank(t)表示t 所表示的城市在推荐集合中排名，mrr@k值越高越好，表示我们预测命中的结果在我们的推荐集合中的顺序更靠前。

4.3 结果分析

本文在三个不同的数据集上都进行了实验，图结构模型在两个指标下均取得了更好的实验效果，这表明本文使用的基于图神经网络与注意力机制的模型对解决旅客后续行程预测问题上具有高度的匹配性,能够更好的解决本文提出的问题。

从表2 中可以看出，基于旅客历史记录中城市所出现的频率进行推荐目的地的方法FF 在各个数据集上取得了不错的效果，均超越了主流的时序预测模型GRU 与点击率预测模型STAMP，但其mrr@5 指标始终较低，说明在其预测的结果候选集中，真实目的地的排名比较靠后，而图结构模型的实验结果在hr@5 和mrr@5 两个指标上均优于其他所有的方法。

5 结论

本文针对旅客后续行程预测的问题，通过对旅客出行数据的分析，结合当前各个领域对序列预测的研究，寻找到了一种基于图结构模型的预测方法。通过图神经网络对旅客的历史出行城市序列进行建模，与全局航线网络结合，同时考虑旅客的历史出行兴趣与当前所在城市的重要性，并引入注意力机制，实现对行程未预定完成旅客的后续行程预测，解决了民航旅客出行模式多样化、出行记录稀疏和出行间隔不规则等难点，以及跳出了旅客个体出行受到外界因素影响的问题，从旅客个体历史出行序列出发，并在真实的旅客出行数据集上进行了实验，实验证明图结构模型具有更好的预测效果。

表1：实验数据集

表2：不同方法在三个数据集上的实验结果