二级剪叉式液压升降机液压缸布置方式研究

□ 西庆坤 □ 杨德辉 □ 李兴慧

四川工程职业技术学院 机电工程系 四川德阳 618000

1 研究目标

剪叉式升降机具有结构简单、运行平稳、操作简便等优点,广泛应用于航空航天、交通运输等各种升降设备中[1-2]。近年来,很多学者对不同形式的剪叉式液压升降机进行了研究。于永江等[3]应用虚位移原理,对多级剪叉式液压升降机液压缸推力进行了求解,并对剪叉杆进行了受力分析和强度校核。文献[4]应用MATLAB软件综合分析了一级剪叉式升降机的关键参数。郑玉巧等[5]对一级剪叉机构进行了力学分析,并对液压缸安装位置进行了优化设计。胡小舟等[6]对小承载力的二级剪叉式液压升降机进行力学分析,推导出液压缸推力、载重力与机构尺寸参数之间的关系。在剪叉式液压升降机设计过程中,设计参数不同,剪叉式液压升降机剪叉级数不同，液压缸安装位置也不同。笔者对二级剪叉式液压升降机液压缸布置方式进行研究,分析计算大承载力二级剪叉式液压升降机液压缸的推力,并应用MATLAB软件对液压缸的安装位置进行优化设计,进而减小液压缸推力,减少能源消耗。

二级剪叉式液压升降机设计参数见表1。台面尺寸为3 600 mm×2 000 mm,最低高度为700 mm,上升高度为4 800 mm,载重力P为2 000 N,经计算得剪叉杆两端铰接孔中心距L为3 000 mm。剪叉机构处于最低位置时，液压缸的推力最大[7],此时剪叉杆与水平方向的起始角αmin为6.7°。剪叉机构处于最高位置时，剪叉杆与水平方向的夹角αmax为66°。

表1 二级剪叉式液压升降机设计参数

2 液压缸布置方式

二级剪叉式液压升降机中，液压缸布置方式主要有三种。

(1) 液压缸竖直布置。液压缸下端固定在机架上,液压缸上端活塞与上板连接。采用此种布置方式，液压缸的升降行程等于升降机的提升高度,整机结构庞大。

(2) 液压缸水平布置。通过分析计算可知,此时液压缸的推力最大,且液压缸受横向力作用,影响密封件的使用寿命[8]。

(3) 液压缸倾斜布置。采用双铰接结构,避免上述两种布置方式的缺点,并且平台的升降行程可以达到液压缸行程的两倍以上。在工程中常采用液压缸倾斜布置方式，因此笔者重点研究此种布置方式。

液压缸倾斜布置具体可细分为两种形式[8]。第一种，液压缸底端固定在靠近剪叉机构固定铰接支座一端,液压缸的行程比较短,但液压缸推力较大,使液压缸的直径增大,进而使机构难以布置。第二种，液压缸底端固定在靠近剪叉机构活动铰接支座一端,液压缸推力小,且直径小,便于整机布置,此时液压缸的升降行程长,但如果整机升降高度不大,那么液压缸行程的增量也是有限的。

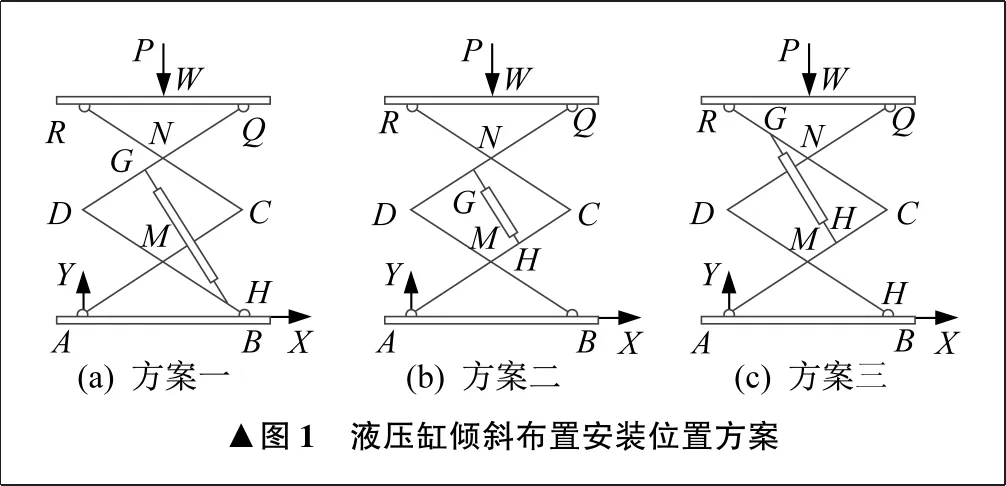
笔者分析的液压缸,底端固定在靠近剪叉机构活动铰接支座一端。此时又有如图1所示三种液压缸安装方案。C点、D点为上下两级剪叉杆的铰接点，R点、Q点为升降平台与剪叉杆的铰接点，N点为剪叉杆RC与QD的铰接点，M点为剪叉杆BD与AC的铰接点，A点、B点为机架与剪叉杆的铰接点，W点为载重力P作用点，G点、H点为液压缸活塞杆铰接处。液压缸下端常安装在底层剪叉机构上,方便液压元件的安装,所以方案三与方案一相比不可取。方案二液压缸的安装距离和行程小于方案一,举升力和举升高度小于方案一。通常采用双液压缸并联形式,但要解决液压缸的同步问题。相对而言，方案二适用于小型升降装置。对于大型升降装置,液压缸安装均采用方案一,且方案一液压缸安装接近底板,较为方便。综上所述,对于二级剪叉式液压升降机,液压缸安装常采用方案一与方案二,方案一适用于承载力大和升降高度大的场合,方案二适用于承载力小和升降高度小的场合。

笔者研究的二级剪叉式液压升降机液压缸采用安装方案一，而对于液压缸具体安装在哪个位置时推力最小,现有文献则尚未进行研究。对此，笔者应用虚位移原理来计算求解液压缸推力,然后以液压缸推力最小为目标，建立优化设计数学模型,应用MATLAB软件进行优化设计,得到液压缸推力最小时对应的安装位置。

3 液压缸推力求解

二级剪叉式液压升降机的动力学分析模型如图2所示,整个剪叉机构为平衡对象,载重力P和液压缸推力F为主动力,铰接约束为理想约束。根据虚位移原理，作用于质点系的主动力在任何位移中所做虚功的和等于零[9]，即:

∑(Xiδxi+Yiδyi+Ziδzi)=0

(1)

式中:Xi、Yi、Zi为作用于质点系mi的主动力Fi在直角坐标轴上的投影；δxi、δyi、δzi为虚位移δri在直角坐标轴上的投影。

图2中θ为液压缸安装位置与水平方向的夹角，a为液压缸上端距上层两剪叉杆铰接点的距离，b为液压缸下端距下层两剪叉杆铰接点的距离，W点Y轴方向的坐标Wy为:

Wy=2Lsinα

(2)

式中:α为剪叉机构剪叉杆与水平方向的夹角。

式(2)经变分运算得:

δWy=2Lδαcosα

(3)

式中：δWy为W点在Y轴方向的微位移；δα为角α的微角位移。

H点坐标(Hx,Hy)、G点坐标(Gx,Gy)为:

(4)

(5)

式(4)、式(5)经变分运算得:

(6)

(7)

式中：δHx为H点在X轴方向的微位移；δHy为H点在Y轴方向的微位移；δGx为G点在X轴方向的微位移；δGx为G点在Y轴方向的微位移。

在G点处,Y轴方向微位移与X轴方向微位移之间的夹角为β。在H点处,Y轴方向微位移与X轴方向微位移之间的夹角为ψ。于是有:

(8)

(9)

虚功方程为:

-PδWy+FcosβδGx+FsinβδGy-FcosψδHx

-FsinψδHy=0

(10)

式(10)化简得:

(11)

将式(3)、式(6)、式(7)代入式(11),得:

F=2PLcosα/{cosβ[(L/2-a)sinα]

-sinβ[Lcosα+(L/2-a)cosα]

-cosψ[(L/2+b)sinα]

+sinψ[(L/2-b)cosα]}

(12)

式(12)为液压缸推力F与载重力P的关系式。若载重力P确定,且剪叉杆两端铰接孔中心距L、液压缸上端距上层两剪叉杆铰接点距离a、液压缸下端距下层两剪叉杆铰接点距离b、剪叉杆与水平方向夹角α已知,则可由式(12)求出液压缸推力F。

4 优化设计数学模型

4.1 设计变量

笔者对二级剪叉式液压升降机液压缸的安装位置进行优化设计,将液压缸上端距上层两剪叉杆铰接点距离a作为设计变量x1,将液压缸下端距下层两剪叉杆铰接点距离b作为设计变量x2,则优化设计变量X为:

X=(x1,x2)T=(a,b)T

(13)

4.2 目标函数

在载重力P和剪叉杆两端铰接孔中心距L一定的条件下,以液压缸推力F为目标函数F(x),即:

F(x)=Minf(x)=2PLcosα/

{cosβ[(L/2-a)sinα2]

-sinβ[Lcosα+(L/2-a)cosα]

-cosψ[(L/2+b)sinα]

+sinψ[(L/2-b)cosα]}

(14)

4.3 约束条件

液压缸上端应安装在铰接点N和铰接点G之间或之上，则约束条件g1(X)和g2(X)为:

g1(X)=0-a≤0

(15)

g2(X)=L/2-a≤0

(16)

液压缸下端应安装在铰接点M和铰接点H之间或之上，则约束条件g3(X)和g4(X)为:

g3(X)=0-b≤0

(17)

g4(X)=L/2-b≤0

(18)

4.4 数学模型

综上所述,以液压缸推力F最小为目标函数的优化设计数学模型为:

X=(x1,x2)T=(a,b)T

F(x)=minf(x)=2PLcosα/

{cosβ[(L/2-a)sinα2]

-sinβ[Lcosα+(L/2-a)cosα]

-cosψ[(L/2+b)sinα]

+sinψ[(L/2-b)cosα]}

5 优化结果

应用MATLAB软件对液压缸安装位置进行优化设计[10]，子程序为：

function F=myfun113(x)

L=3000;

P=20000;

a=pi*8.06/180;

b=pi+atan((L*cos(a)+(L/2-x(1))*cos(a))/((x(1)-L/2)*sin(a)));

u=pi+atan((L/2-x(2)*cos(a))/(-(L/2+x(2))*sin(a)));

F=-P*L*cos(a)/(-cos(b)*(x(1)-L/2)*sin(a)-sin(b)*(L*cos(a)+(L/2-x(1))*cos(a))-cos(u)*(L/2+x(2))*sin(a)+sin(u)*((L/2-x(2))*cos(a)));

>> clear all

L=3000;

P=2000;

a=pi*6.7/180;

A=[-1,0;0,-1;1,0;0,1];

B=[0;0;L/2;L/2];

x0=[1000,700]

[x,F]=fmincon(@myfun1113,x0,A,B)

运行结果为：

x= 0 1441.1

F=1.4689e+004

优化设计结果见表2。由表2可知，a为0 mm,b为1 400 mm,液压缸上端安装在上层两剪叉杆的铰接N点,液压缸下端安装在距离下层两剪叉杆的铰接M点1 400 mm处。剪叉式液压升降机通常有前后两套剪叉机构,所以液压缸上端应安装在前后N点处两连杆的中间,下端应安装在下层前后H点处两连杆的中间。优化后液压缸活塞推力减小了35.3%,提高了二级剪叉式液压升降机的效率和传动质量。

6 液压缸行程

表2 液压缸安装位置优化设计结果

设液压缸长度为I,行程为S，通过底层剪叉杆与水平方向的夹角最小值αmin可以求出液压缸的最小长度Imin,通过底层剪叉杆与水平方向的夹角最大值αmax可以求出液压缸的最大长度Imax,则液压缸的行程S为:

S=Imax-Imin

(19)

由图2有：

(20)

(21)

根据设计参数,αmin为6.7°,αmax为66°,a为0,b为1 400 mm,L为3 000 mm，代入式(20)、式(21)，可求得:

Imin=1 482 mm

Imax=4 060 mm

由式(19)求得液压缸行程为2 578 mm。

7 结束语

二级剪叉式液压升降机液压缸采用两铰接方式,液压缸底端铰接在滑动端是理想的安装位置。

根据虚位移原理，得到二级剪叉式液压升降机液压缸推力公式。以液压缸推力最小为目标函数,应用MATLAB软件进行优化设计，求解液压缸的最佳安装位置,从而减少能源消耗。

对于一级、小型或大型二级，以及多级剪叉式液压升降机，液压缸推力都可以采用虚位移原理进行求解,笔者所采用的方法具有推广价值。