细砾质斜坡海床上波浪的传播特性试验

张继生,钱方舒,童林龙,韦 超,蒋裕丰

(1.河海大学海岸灾害及防护教育部重点实验室,江苏 南京 210098;2.河海大学港口海岸与近海工程学院,江苏 南京 210098; 3.南京河海科技有限公司,江苏 南京 210016)

波浪与海床之间的相互作用是土动力学和海岸动力学间的交叉学科,是海岸动力学研究领域的前沿和重点课题[1-2]。波浪与海床之间的相互作用机制十分复杂,一方面,波浪作用下海床动力响应规律与海床土体的性质密切相关,不同类型海床在相同波浪荷载作用下的响应机制具有明显差异[3];另一方面,海床土体动力响应对波浪传播过程中水底边界条件影响显著,进而对波浪的传播演变规律也具有重要影响[4-5]。

海床的稳定性与波浪作用下的海床动力响应有关。波浪传播过程中在波浪与海床交界面上产生动水压强,从而引起海床土体中有效应力和孔隙水压力在时间及空间上的不均匀变化。当波浪作用于砂质海床时,由于海床土体粒径较大,渗透性较好,在波浪作用下超静孔隙水压力的响应具有周期性振荡特征[6];当波浪作用于粉砂质或黏土海床时,细粒土的渗流通道狭窄,孔隙流体较难排除且波浪荷载作用土骨架会发生残余变形,导致孔隙水压力逐渐累积[7-8]。海床土体内有效应力及孔隙水压力的上述变化可能导致土骨架发生剪切破坏或者液化,导致海工结构物失稳。

传统波浪理论中通常假设海床表面为刚性、不可渗透边界,而海洋土体属于可渗透的多孔介质[9],海床表面法向速度分量不为零。当海床土体为松散的细颗粒泥沙时,渗流作用较弱,波浪的传播规律受床面变形的作用更为显著[10-11];但当海床土体由粗颗粒泥沙构成时,床面变形较小,渗流作用对波浪传播特性的影响更加显著[12-13]。基于线性波浪理论,Putnam[5]推导了波浪运动过程中受渗流作用而引起的波能耗散率。由于波峰波谷的压力差,水质点会透过可渗透介质的孔隙流进和流出而发生渗流损失,但只适用于渗流较小的情况。Reid等[14]指出Putnam[5]的结果只适用于渗流引起能量耗散较弱的情况。Liu[15]研究了波浪传播过程中的黏性耗散和渗流耗散作用。刘忠波等[12]推导出了适用于渗透海床的Boussinesq方程,改进后模型的计算结果与前人的解析结果更加吻合。在海床渗透系数对波浪传播的影响方面,王忠涛等[9]用理论分析方法讨论了海床条件对波幅衰减和波长变化的影响。唐志波等[13]通过数值算法研究了不同渗透系数以及不同水深条件下波浪传播过程中波高的衰减规律。Tong等[11]通过试验研究了海床发生液化时波高沿程的衰减,入射波浪条件对波高衰减有一定的影响。

上述研究侧重于探讨常水深条件下渗流对波浪传播特性的影响机理,而近岸地区多为斜坡地形。波浪在斜坡上传播时,随着相对水深的减小,波浪发生浅水变形,变形过程伴随着渗流耗散作用,波浪的演变机制十分复杂。为了增进波浪在渗透性良好的斜坡海床上传播演变机制的认识,笔者在水槽中开展斜坡海床上波浪传播特性试验,观测波浪与细砾质海床相互作用过程中的海床动力变化、近底流速和自由液面变化,研究波浪在可渗透斜坡海床上的传播演变规律。

1 试 验 方 案

1.1 试验布置

图1 试验布置(单位:m)Fig.1 Experiment layout (units: m)

试验在海岸灾害及防护教育部重点实验室波浪水槽中进行,水槽长35 m、宽0.5 m、高1 m,水槽两侧为光滑透明的钢化玻璃,一端布置了多孔泡沫用于消波,另一端安装有液压活塞式造波机用于造波。试验水槽中间布置有5 m长的砂槽,试验通过在砂槽中铺设细砾质土模拟细砾质海床。为了方便,采用笛卡尔直角坐标系对水槽进行划分,波浪传播方向为x轴正方向,水槽横断面方向为y轴正方向,z轴为竖直方向(图1),y轴和z轴正方向根据右手定则确定,坐标原点O位于砂床表面处。在砂槽上方布置11个电容式浪高仪,测量沿程自由水面位移;在斜坡上x=3.5 m处沿垂向布置了3个微型芯片式孔隙水压力传感器(探头直径0.6 cm,长1 cm,下文简称孔压传感器),孔压传感器的间隔为8 cm,用于测量波浪运动过程中海床内超静孔隙水压力;为研究波浪边界层附近的水动力特征,采用小威龙剖面流速仪(简称流速仪)测量了斜坡上沿波浪传播方向4个剖面(P1、P2、P3、P4)处的近底流速,每2个剖面之间的间隔为0.5 m。浪高仪和孔压传感器的精度均为0.1%,流速仪可以单次测量探头以下4 cm的剖面上30个点的流速,剖面分辨率为1 mm,测量精度为0.5%。试验中浪高仪和孔压传感器布置的具体位置如图1所示,流速仪布置所选4个剖面分别位于距离斜坡起点1.75 m、2.25 m、2.75 m、3.25 m处(x=2.75 m、x=3.25 m、x=3.75 m、x=4.25 m,图1)。采用电容式浪高仪和流速仪同步测量波浪传播过程中的自由液面位置和近底流速,流速仪的采样频率设置为50 Hz,浪高仪和孔隙水压力传感器的采样频率均设置为100 Hz。

1.2 试验条件

试验中所用的砂砾为经过筛选的石英细砾,其平均粒径d50为3.71 mm,相对密度Dr为0.69,孔隙率ns为0.39,土样的颗粒密度ρs为2.66×103kg/m3,渗透系数ks为1.4×10-2m/s。波浪与细砾质海床相互作用过程中,海床内的细砾质颗粒位移并不明显,水体十分清澈,无沙纹产生,在埋设孔压传感器断面处的海床地形高程也无变化。为了讨论斜坡前水深h、特征波高H和波浪周期T的影响,设置了7组工况,各组次所对应的试验条件和无量纲参数见表1,表中H和T为砂槽入口处的特征波高和波浪周期,L为按照线形波浪理论计算的砂槽入口处的特征波长,这7组试验工况均无波浪破碎现象。为了描述砂槽入口处波浪的非线性程度,引入描述波浪特性的无量纲参数:波浪的非线性参数ε=H/(2h)、相对水深μ=kh(其中波数k=2π/L)和厄塞尔数Ur=HL2/h3,各工况具体参数见表1。

表1 试验条件和无量纲参数

图2 试验中超静孔隙水压力的幅值沿垂向的分布Fig.2 Vertical distributions of the amplitude of wave-induced excess pore water pressure

2 试验结果与讨论

2.1 超静孔隙水压力

海床在正负交变的波浪荷载作用下,内部会形成渗流,同时海床内的超静孔隙水压力也会相应发生改变。由图2可知,改变波浪入射波高和周期,海床中超静孔隙水压力幅值|p|max变化趋势基本相同,波浪引起的超静孔隙水压力幅值均随波高和周期的增加而增加。图2中z表示埋设孔压计剖面位置处以砂床表面为原点竖直向上的距离。根据Liu等[16]的研究,当海床厚度一定时,超静孔隙水压力在海床中的扩散距离可以表示为

(1)

式中:Lz——海床中超静孔压扩散的垂直距离;K——波浪的有效体积弹性模量;ρ——流体密度;g——重力加速度。

根据式(1),当入射波浪周期增大时,超静孔隙水压力垂直扩散距离增大,在海床中可以扩散更深的距离。海床中超静孔隙水压力随着扩散深度的增加而减小,且周期大的波浪作用下海床中超静孔隙水压力较大。当入射波浪波高增大时,波浪与海床交界面处的孔隙水压力增大,则海床中的超静孔压也相应增大。由图2可知,在本试验海床超静孔压的测量范围内,海床内波浪引起的超静孔隙水压力在床面附近衰减较快,海床8 cm以下超静孔隙水压力衰减较慢,这表明在海床表层处,超静孔隙水压力扩散较快,随着扩散距离的增大,超静孔隙水压力衰减逐渐缓慢,即海床中的渗流速度随着海床深度的增加而逐渐减小。

2.2 近底水平流速特征

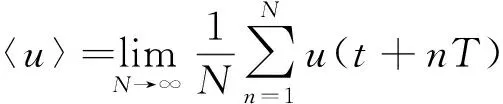
(2)

式中:N——统计波数,试验中采用连续的10个周期内时均流速进行分析,即取N=10;t——试验测量时间。

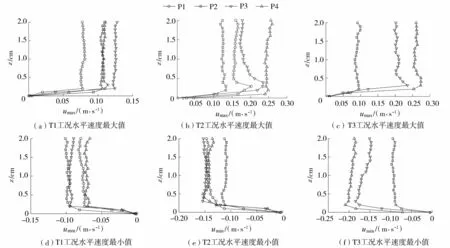
图3 近底边界层内水平速度最大值和最小值沿水深方向的分布Fig.3 Vertical distributions of maximum and minimum horizontal velocities in near-bottom boundary layer

研究中根据式(2)计算4个剖面的近底水平流速,图3分别给出了T1、T2、T3工况近底水平流速最大值和最小值沿水深方向的分布。由图3可以看出,当波浪经过1 m长的平坡进入斜坡海床发生浅化后,受到非线性的影响,近底水平流速具有明显不对称特征。其中T3工况的P4剖面处由于水面接触流速仪,产生碎波无法测量,故只测量了前3个剖面的流速变化特征,如图3(c) (f)所示,图中正值表示向岸流速,负值表示离岸流速。对比各剖面最大和最小流速分布,近底水平流速分布呈现向岸方向的速度幅值大于离岸方向的速度幅值的特征。随着波浪在斜坡上传播距离增加,波浪浅化特征越来越明显,近底水平流速的幅值也随之增大。出现P1处近底水平流速幅值比P2处大的情况是因为P1剖面位于斜坡前缘,波浪经过1 m长平坡的传播,斜坡对它的影响还比较小,波浪传播到P2剖面时,由于斜坡上细砾质海床的渗流更大,波浪能量会有一定程度的衰减,底部波浪近底层内的流速相应变小。图3(a)～(c)可以看出,在同一入射波浪周期条件下,入射波高越大,波浪近底水平流速越大。这是因为入射波高的增大使得波浪在斜坡上的浅化增强,加剧了波浪波峰和波谷的不对称性,因此近底水平流速也会相应变大。

此外,波浪在细砾质海床上传播时,受海床内渗流的影响,水质点会通过细砾质海床的孔隙进入海床内部,因此在波浪与海床交界面上的流速并非为0,而是在床面处存在一个较小的速度。例如图3(b)(d)所示,P1床面处的最大向岸流速和最大离岸流速分别为0.002 m/s和0.004 m/s,P2中床面处分别为0.005 m/s和0.004 m/s,P3中床面处分别为0.008 m/s和0.006 m/s,P4中床面处分别为0.009 m/s和0.011 m/s。

2.3 自由液面变化特征

由于受到近岸海床地形和浅水变形的影响,浅水地区波浪的非线性特征会愈加显著,而波浪浅水变形的几何特征是描述波浪非线性性的重要依据之一。

图4分别为T1、T2、T3、T5工况同一相位的波浪经过入口处(1号浪高仪)和出口处(11号浪高仪)的波形图。由图4可知,这4组试验中入射波浪较为规则,具有斯托克斯波波形特征,且随着波高、周期的增大,波峰波谷不对称更加明显。波浪经过斜坡后,受浅水变形作用,波形水平不对称和峰谷不对称现象更加显著。如图4(a)～(c)所示,当入射波高为5.66 cm时,11号浪高仪处波形较为光滑,波高较为陡峭,波谷较为平坦;而当波高增大到7.00 cm和8.12 cm时,11号浪高仪的波形较为不规则。结合砂槽入口处(1号浪高仪)的波浪厄塞尔数进行分析,试验T1工况中,砂槽入口处波浪的厄塞尔数为8.23,波谷传播时间与波峰相比稍有延长,峰谷时间比为0.67;在试验T2工况中,入口处的厄塞尔数增大到10.18,出口处的波形与入口处相比有较大差异,波峰传播时间缩短至0.63 s,波谷传播时间增长至1.07 s,峰谷时间比减小至0.59; T3工况,入口处的厄塞尔数进一步增大到11.80,出口处的波形在进入波谷时有一处明显的凹陷,波峰更加尖陡,峰谷时间比仅为0.50。综上,随着斜坡入口处厄塞尔数的增加,波浪的非线性特征越来越明显,即波浪浅水变形程度越来越剧烈。当周期增大时,波形呈现同样的变化特征,如图4(d)所示。

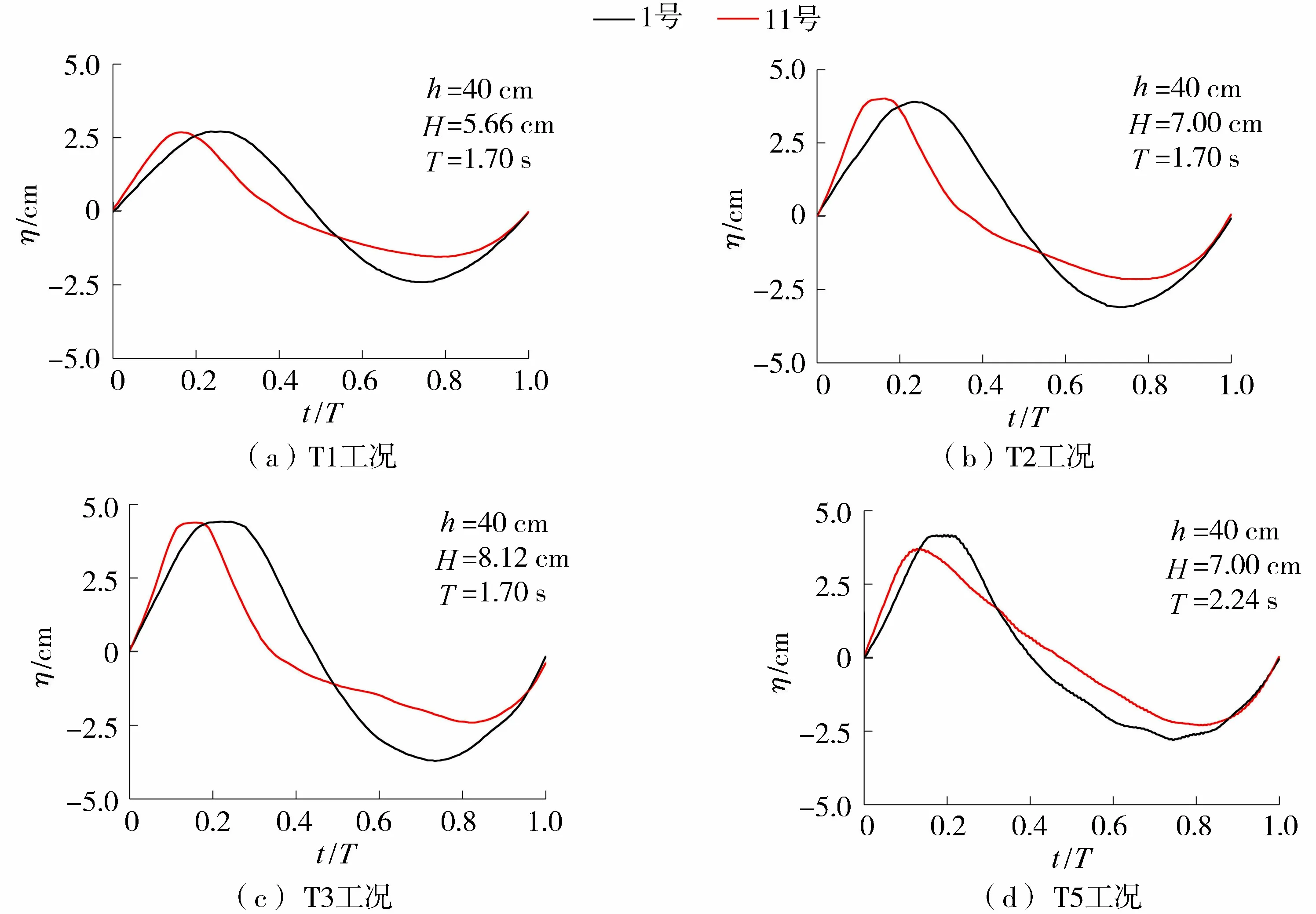
图4 细砾质海床试验自由液面曲线Fig.4 Free surface elevation curves of waves over the fine gravel seabed

为了深入研究波浪在斜坡海床上传播过程中的能量变化,将沿程11根浪高仪所测得的波形进行模态分析,计算各阶谐波的波高和能量,阐明波浪在砂槽上方传播过程中各阶谐波波幅的沿程变化特征,进一步揭示波浪的运动规律。波面η的变化函数采用特征波幅进行无量纲化,可以展开为如下傅里叶级数的形式:

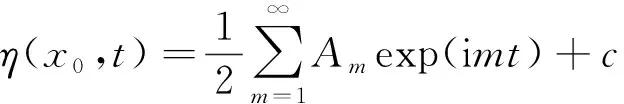
(3)

式中:x0——固定的水平位置;Am(m=1, 2, 3,…)——第m阶谐波的波幅;c——前一项的转置。

波浪总能量E的计算公式定义为

(4)

基于式(3)(4)的模态分析发现,10阶以上谐波对波形的影响小于1%,因此只计算前10阶谐波的波幅,且四阶以上谐波较小可以忽略。由图5可知,一阶谐波的波幅在试验中较大,相应地,一阶谐波的能量占总能量的主要部分。在砂槽入口处,|A1|接近于1,二阶谐波波幅相对较小,基本小于0.2,三阶及四阶谐波波幅更小,分别为0.04和0.02,图5(d)中三阶和四阶谐波分别达到了最大值0.04和0.08。随着波浪在砂槽上方传播距离的增加,一阶谐波的幅值减小,二阶及以上谐波的幅值逐渐增大且该现象在斜坡上方更加明显,对砂槽入口和出口处的能量计算发现波浪能量也有所衰减,这说明波浪的各阶谐波之间可以发生能量交换,能量是从一阶谐波逐渐转移到二阶及以上谐波波浪中的,同时波浪总能量受渗流和黏性耗散影响会出现衰减。对比图5(a)～(c),入射波高从5.66 cm增大到7 cm和8.12 cm时,砂槽入口处厄塞尔数相应从8.23增大到10.18和11.80,在砂槽出口处一阶谐波波幅从0.88分别减小至0.84和0.79,二阶谐波波幅从0.30分别增大到0.35和0.40,三阶、四阶谐波波幅也呈现同样的趋势,因此入射波浪的厄塞尔数越大,波浪传播过程中的波-波相互作用也越剧烈。相应地3组试验中波浪在砂槽上方传播过程中波能损失分别为11.9%、13.3%、20.6%。图5(f)(b)(e)分别展示了斜坡前水深为45 cm、40 cm、37.5 cm时前四阶谐波波幅的空间分布规律,斜坡前水深越小,入射波浪相应的厄塞尔数则相对较大。当斜坡前水深为37.5 cm时,砂槽出口处一阶谐波波幅减小至0.74,二阶和三阶谐波波幅分别增大至0.40和0.16,这3种工况的波浪经过砂槽的能量耗散分别为6.3%、13.3%、22.9%。对于周期较大即厄塞尔数较大的波浪,各谐波之间的相互作用时间也随之增加,波-波相互作用相对较强,如图5(d)所示。上述结果表明,波-波相互作用的本质是各阶谐波之间的能量交换,随着厄塞尔数的增大即波浪浅水变形的增强,波浪的各谐波之间的波-波相互作用剧烈,同时波浪在渗透性良好的斜坡海床上的浅水变形还需要考虑渗流耗散的影响。

图5 波浪前四阶谐波波幅在砂槽上方的分布Fig.5 Distributions of wave amplitudes of first four harmonics along the flume

2.4 波浪的衰减和浅水变形

图6展现了斜坡前水深为40 cm时,波浪在细砾质海床沿程波幅变化的理论解和试验结果的对比图。根据Liu等[18]的研究,当不考虑海床的渗透性时,波浪在平坡海床上的波幅衰减的解析表达式为

(5)

式中:a0——入射波浪的波幅;a1——x=1 m处波浪的波幅;2W——水槽宽度;ν——水的黏度。

图6 波浪沿程波幅变化的理论解和试验结果对比Fig.6 Comparison of theoretical and experimental results of wave amplitude variation along the flume

斜坡海床上波浪由浅水变形导致的波幅变化的解析表达式为

(6)

式中:a′——波浪在斜坡海床上的波幅;h′——斜坡海床上的水深。

对比图6(a)～(c)中0～1 m的波幅变化,理论结果显示无渗透性平坡海床对波浪传播作用较小,x=1 m处波幅与入射波浪波幅相比略有减小;而细砾质平坡海床波浪传播的试验结果显示,x=1 m处波幅出现较明显的衰减。入射波高为5.66 cm时,在x=1 m处的波幅衰减了1.5%。当入射波高增大到7.00 cm和8.12 cm时,x=1 m处的波幅衰减相应为1.9%和2.1%。

当波浪在斜坡海床上传播时,理论结果显示波浪由于浅水变形的作用,波幅呈现稳定增大的趋势,入射波高分别为5.66 cm、7.00 cm和8.12 cm的波浪传播到x=4.5 m处的波浪波幅分别增大了14.1%、15.2%和15.5%。而对比细砾质海床的试验结果,在渗透性和浅水变形共同作用下,波浪在斜坡的前半段(x<3.5 m)即浅水变形的初段,波幅呈现先增大后减小的趋势;在x=3.5 m左右处,波幅衰减到最小,即海床的渗透作用大于波浪浅水变形作用。由图6可知,波幅分别减小了4.0%、2.6%和2.6%;波浪继续在斜坡上传播(3.5 m

3 结 论

a. 海床中超静孔隙水压力的垂直扩散距离随着波浪周期的增大而增大,即入射周期较大的波浪作用下海床中超静孔隙水压力较大;入射波高的增加使海床表面处的孔压增大,同样导致海床中的超静孔隙水压力较大。

b. 波浪近底水平流速随着波浪浅水变形程度的增大而增大,且受海床渗流的影响,在波浪与海床交界面上的流速并非为0,而是在床面处存在一个较小的速度。

c. 入射波浪厄塞尔数越大,斜坡上波浪浅水变形越明显;波-波相互作用的本质是各阶谐波之间的能量交换,厄塞尔数大的波浪各谐波之间的波-波相互作用剧烈,同时波浪在渗透性良好的斜坡海床上的浅水变形还需要考虑波能耗散的影响。

d. 在浅水变形初段,海床渗透作用大于波浪浅水变形作用,在浅水变形剧烈区域,波浪浅水变形作用大于海床渗透作用。