基于OpenFOAM的异重流数值模拟分析

丁伟业，金 生，林金波

(大连理工大学 海岸和近海工程国家重点实验室，大连 116024)

异重流是指密度相差不大的两种可以相混的流体在适宜条件下因密度差异而产生的相对运动。在运动过程中，各种流体基本能够保持原有的面貌，不因交界面上存在的紊动掺混作用而发生全局性的混合现象。1892年Forel[1]在莱曼湖中首次观察到了携沙水流在注入湖水中时并未与湖水混合，而是潜入到湖水底部形成异重流的现象。作为河流注入汇水体三种方式之一的异重流，1953年由Bates[2]在研究三角洲时给出定义。Mulder和Syvitski[3]于1995年重新修订了Bates关于异重流的定义。他们将异重流定义为一种负浮力的流体。按照产生的原因，异重流可以分为温差异重流(如热电厂冷却池)、盐水异重流(如河口盐水楔)以及浑水异重流(如挖入式港池，水库等)。对于河口地区，上游淡水泄入海洋中，与随潮上溯的咸水混合形成异重流。异重流在其流动的过程中会携带大量的泥沙，随着泥沙浓度的增加，泥沙颗粒构成絮凝团,引起沉降，最终形成淤积。因为港池、船闸、渠道中的流体常常是静止的，具有形成异重流的条件，容易因为异重流的入侵形成淤积进而阻碍航行。因此，关于异重流的研究对于水道港口的正常运行，乃至河口海岸演变有着重要的实际意义。

Keulegan[4]采用实验的方式，获得了一系列的关于异重流锋头速度特性的曲线。Benjanmin[5]指出，当上、下层流体达到渠道半深时，上、下层流体分别以不同的速度前进。在研究异重流流动的过程中Benjanmin发现，能量损失的最大值约为10%，能量损失较少。Shin[6]在完善Benjamin的理论的基础上指出，当Re较大时，异重流的能量耗散可以忽略不计。Hartel[7-9]采用直接数值模拟(DNS)，更细致准确的观察了异重流锋头的形状与特性。Birman[10]在研究异重流锋头空间结构的过程中观察到了Kelvin-Helmholtz (KH)不稳定，与Hartel所观察到的一样，KH涌浪都是成对出现的。Cantero[11]通过二维和三维数值模拟对异重流的锋头结构与速度等相关特性进行了研究。他指出通常高Re情况下，二维异重流的模拟中界面处翻滚的涡更为强烈。

为了更清楚的了解异重流的结构以及相关特性，本文利用开源计算软件OpenFOAM对异重流的进行数值模拟。利用有限体积法对控制方程进行离散，PISO算法对方程进行求解。每一个PISO算法的内迭代步中的压力梯度通过压力泊松方程来求解[12]。

1 数值模型

本文研究的异重流是由不同密度的流体相对运动引起的。相应的数值模型的基本微分方程包括连续方程，雷诺时均方程以及输运方程。

▽·u=0

(1)

(2)

其中：t为时间；u=(u,v)为笛卡尔坐标系下的速度矢量场；ν为动力粘度；ρ为流体密度；p*=p-ρg·x为修正压力；g为重力加速度；x=(x,y)为笛卡尔坐标。

流体密度的变化是一个对流-扩散的过程。相应的方程为

(3)

式中：Dm为分子耗散系数；Sct=νt/Dk为紊流施密特数；νt为涡粘度；Dk为涡耗散。

2 模型验证

如图1所示，在平底渠道中两种不同密度的流体被闸门分隔。当闸门被抽取后，密度大的流体向下流动，密度小的流体向上流动，此过程被称作异重流。许多研究人员花费大量的精力通过实验[13]或者数值模拟[9, 14-16]来研究异重流发生过程中的细节。作为经典算例，异重流特别适合用来验证非静压海洋模型。在异重流发生的过程中，包含了切应力驱动的流体混合和内波。流体粘性的大小以及模型的精度均会对异重流产生明显的影响。

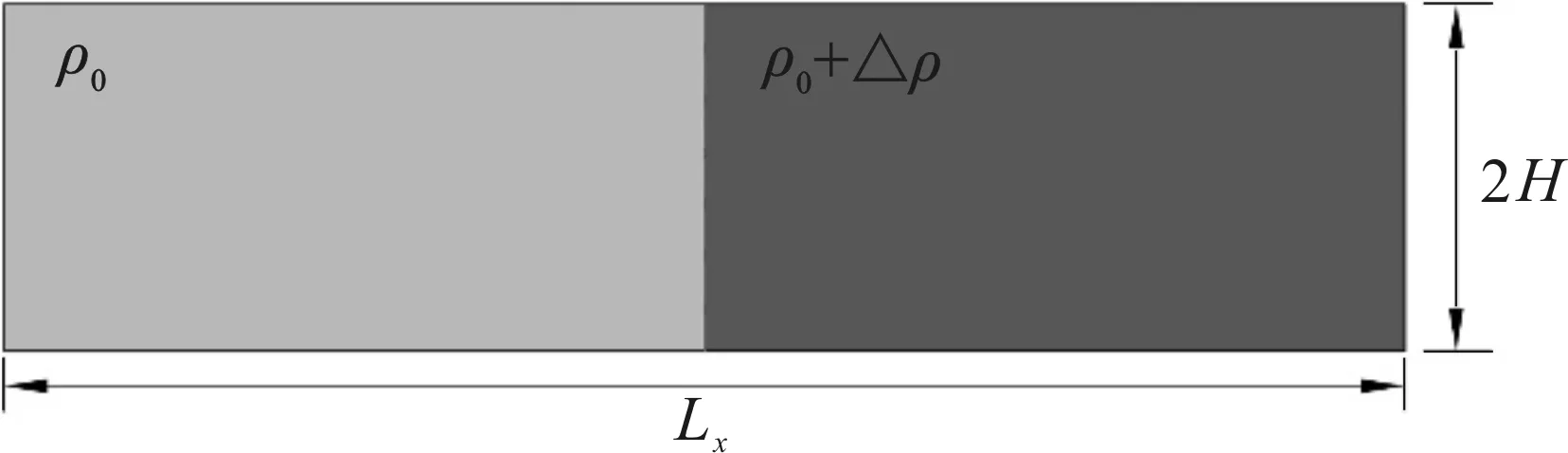
图1 计算域示意图Fig.1 Schematic illustration of lock-exchange

表1为5T时刻不同计算域离散尺度的异重流特征值收敛性分析。根据Berntsen[14]描述，xf=(x-Lx/2)/H为ρ0+△ρ/2处最小的x值。大密度流体运动最前端的位置，Umax,min为水平速度的最大值和最小值，Wmax,min为垂向速度的最大值和最小值。在收敛性分析算例中粘度为1E-6 m2/s。由表中结果可知，模拟结果的稳定性与网格精度相关。随着网格精度的增加，采用MS和SS两种离散方法得到的计算结果之间的误差逐渐减小。当网格精度达到1 600×200时，两种离散方法的计算结果最为相近。在后文的模拟过程中，均采用1 600×200网格精度。

表1 收敛性分析， γ= 1E-6 m2/sTab.1 Convergence analysis with 1E-6 m2/s

表2 v= 1E-6 m2/s时本文的数值模拟结果与Berntsen的结果对比Tab.2 Comparisons in the simulations with v=1E-6 m2/s between the present results and the results from Berntsen

表2为5T时刻，粘度为1E-6 m2/s情况下，本文采用的模型与Berntsen[14]模拟结果的对比。从表2中可知，MS与SS获得的Umin，Umax和Wmin存在明显的差值。这表明动量离散格式对模拟结果有着重要的影响。MS模拟的结果与BOM模型的结果相近，SS模拟的结果则与MITgcm模型给出的结果相近。MS与BOM各特质值之间的误差分别为0%，1.95%，2.98%，0.72%和1.86%。SS与MITgcm各特质值之间的误差分别为2.7%，1.68%，0.37%，0.96%和1.16%。

图2 数值模拟异重流时空演化Fig.2 Temporal and spatial variations for the lock-exchange calculated using numerical model

图2为v= 1E-6 m2/s情况下，采用MS方法模拟的异重流流场演化过程。从图2中可以观察到，当在异重流传播过程中，其两种流体的头部均形成James[17]所述的膨胀波。当异重流演化一段时间后，轻流体前缘的膨胀波仍然稳定，然而在膨胀波影响下重流体前缘产生了耗散。如图2-b所示，在膨胀波后方，有内涌浪形成。从图2-a～2-c中可以看出，界面处的两种流体从层流过渡成为紊流。两种流体以不同的速度传播。流体界面因剪切速度变得不稳定，进而不断生成涡。对于由不同密度的连续流体形成的异重流而言，不同速度的流体在界面处的不稳定现象可以用Kelvin-Helmholtz (KH)不稳定来描述。KH不稳定状态下生成的涡称为KH涡。从图2-b中可以观察到，在锋头后方的第一个KH涡更为明显。随着KH涡逐渐掺混到重流体，两种流体界面处形成混合涡，如图2-d所示。在前进的异重流锋头后方，有新的KH涡生成。此时，重流体锋头的高度近似为H。

3 异重流特征值分析

图3和图4分别为5T和10T时刻采用v= 5.6E-8 m2/s, 1E-6 m2/s, 2E-6 m2/s和5E-6 m2/s四种粘度的密度分布。图中变换后的无量纲坐标为x1=(x-Lx/2)/H和z1=(z-H)/H。由图3展示的结果可见，SS的耗散性小于MS。这表明动量方程的对流格式对密度的分布有重要的影响。当粘性为5.6E-8 m2/s和1E-6 m2/s的时候，MS与SS的结果具有明显的差别。粘度为5.6E-8 m2/s时，在SS模拟的结果中可以捕捉到更多小尺度的涡，这与BOM模型获得的结果相一致。然而，当v=1E-6 m2/s时，可以观察到相对小尺度的中等涡，这表明MS得到的结果与MITgcm模型获得的结果几乎完全一致。在Ai[16]和Hartel[9]都能观察到类似的结果。由此可知，本文所采用的模型能够精确的模拟异重流。当使用粘度2E-6 m2/s和5E-6 m2/s时，MS和SS在5T时刻得到的密度分布之间的差别已经非常小了，并且均与BOM模型得到的结果相近。

注:左侧栏为MS方法的结果,右侧栏为SS方法的结果。从上到下的粘度为5.6E-8m2/s,1E-6m2/s,2E-6m2/s和5E-6m2/s。图3 5T时刻密度分布Fig.3Resultsofdensitydistributionsat5T

相比于5T时刻，10T时刻异重流发展的更为充分。通过图4可以观察到，当v= 2E-6 m2/s和5E-6 m2/s时，流场内的涡关于点(0,0) 近似对称分布。随着粘度的减小，密度场的涡分布逐渐变得复杂。MS得到的密度场的耗散性强于SS得到的密度场。在采用SS方法计算的密度场中能够观察到更多小尺度的复杂涡。

注:左侧栏为MS方法的结果,右侧栏为SS方法的结果。从上到下的粘度为5.6E-8m2/s,1E-6m2/s,2E-6m2/s和5E-6m2/s。图4 10T时刻密度分布Fig.4Resultsofdensitydistributionsat10T

表3 前缘速度Uf，Froude数Fr和Reynolds数Re本文的数值模拟结果与Berntsen的结果对比Tab.3 Comparisons of front speed Uf, Froude number Fr and Reynolds number Re between the present results and the results from Berntsen

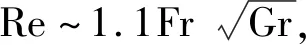
4 结论

本文利用开源CFD软件OpenFOAM对异重流进行了数值模拟，并对其演化过程中的结构变化以及特征值进行了分析。异重流在传播过程中，两种流体前缘均会形成膨胀波。相对于上层的轻流体，膨胀波会对重流体前缘的耗散产生更明显的影响。在膨胀波后方会有内涌浪生成。由于上、下两层流体以不同的速度传播，流体界面会产生KH不稳定现象，进而形成KH涡。随着异重流的演化，KH涡不断与重流体混掺，进而生成混合涡。当异重流稳定传播时，其前缘高度为水槽高度的一半。通过对不同粘性的异重流模拟发现，流体粘性越大，异重流演化过程中的耗散现象越明显。在数值模拟过程中，动量方程的离散格式对模拟的结果有着显著的影响。当流体粘性较小时，采用MS方法模拟的异重流耗散现象比SS方法得到的结果更为明显。通过对异重流特征值的分析可知，MS方法与BOM模型得到的结果更为接近，SS方法与MITgcm模型得到的结果拟合的更好。