基于主成分分析与BP神经网络的TBM围岩可掘性分级实时识别方法研究
段志伟, 杜立杰, *, 吕海明, 王家海, 刘海东, 富勇明
(1. 石家庄铁道大学, 河北 石家庄 050043; 2. 中铁十九局集团第一工程有限公司, 辽宁 辽阳 111000)
0 引言
随着我国公路、铁路、水利工程建设的蓬勃发展,越来越多的TBM投入到隧道工程建设中,成为很多长隧道施工的首选方案,甚至很多包含非常复杂不良地质的隧道也采用TBM与钻爆法协同施工。在TBM掘进过程中,由于刀盘刀具贴合掌子面掘进以及护盾结构本身的限制,TBM主操作手无法直接看到前方地质条件,不能及时判断施工风险和合理调整掘进参数。因此,探索适合TBM施工的围岩可掘性分级方法,建立可掘性等级,并实时识别预警,对TBM安全高效掘进至关重要,这也是未来TBM智能化掘进的重要基础。
目前,业界还缺少公认的适合TBM施工的围岩等级分类理论方法和规范,文献[1-4]采用一系列围岩力学参数对TBM围岩可掘性等级进行分类,但未结合TBM掘进性能。文献[5]基于围岩力学参数及TBM掘进参数,通过求和的方法对围岩等级进行综合分类,但其主要适用于双护盾TBM,且需要7个指标来对围岩可掘性等级进行分类,实际应用时较为繁琐。实际上,TBM掘进过程中围岩可掘性分级考虑的因素很多,围岩力学性能只是一方面,不良地质支护对掘进延误程度、安全风险等都是限制TBM施工围岩可掘性分级的重要因素。因此,应建立基于现场TBM掘进性能与施工风险的围岩可掘性分级方法。
上述研究在TBM施工围岩可掘性分级方面已取得一些成果,但尚不能满足实际工程应用要求。因此,本文对TBM在实际掘进过程中不同围岩下的掘进性能以及施工风险进行分析,将传统BQ法定义的围岩等级依据TBM掘进性能与施工风险进行重新分级,并在此基础上结合TBM掘进特征参数指标(单位贯入度的单刀推力FPI、单位贯入度的刀盘转矩TPI)对实际工程中的围岩进行可掘性分级。该方法可以更好地指导TBM掘进与隧洞支护,更加符合实际TBM施工特点,且一定程度上弥补了BQ法在某些ⅢA类围岩工程现场应用中的局限性,减少了许多不必要的支护工作,提高了TBM施工速度。
此外,正在探索中的TBM围岩实时识别预警研究中,有的模型过于复杂,响应时间太慢,导致围岩指示跟不上TBM掘进速度[6-8]; 有的模型过于简单,只考虑1~2个掘进指标对围岩类别进行识别,准确性具有一定的局限性[9-10];有的模型只是单纯地预测前方围岩的1~2个性能指标(如,岩石单轴抗压强度)[11]。这些研究在很多情况下与实际所测出入较大,且对实际施工参考性也不够全面。
上述在围岩实时识别方法上的研究离真正用于实际施工还有距离,需要持续的深化研究,为此本文引进主成分分析法及PCA-BP神经网络法。主成分分析法可以在提取主要原始数据信息的基础上降低原始变量的维度,简化模型。BP神经网络具有强大的非线性分类能力[12]。且迄今,PCA-BP神经网络法大多应用在岩性识别[13]、电力负载预测[14]等方面,而在TBM施工围岩实时识别方面尚未有相关的研究。鉴于此,本文基于7.0 m直径TBM在凝灰岩下的现场掘进数据与地质数据,选取6个典型的TBM掘进性能指标,运用主成分分析结合BP神经网络构建围岩可掘性等级实时识别模型,并设计一个MATLAB程序提高模型对围岩识别的响应速度。
1 不同围岩的TBM掘进性能及围岩可掘性分级
1.1 TBM技术参数
本文依托于新疆EH工程KS隧洞 Ⅳ标段,该标段采用直径7.0 m的敞开式TBM,围岩岩性为凝灰岩、花岗岩以及石英闪长岩等,以凝灰岩为主,单轴抗压强度集中在30~120 MPa,适合TBM施工。TBM主要技术参数见表1。
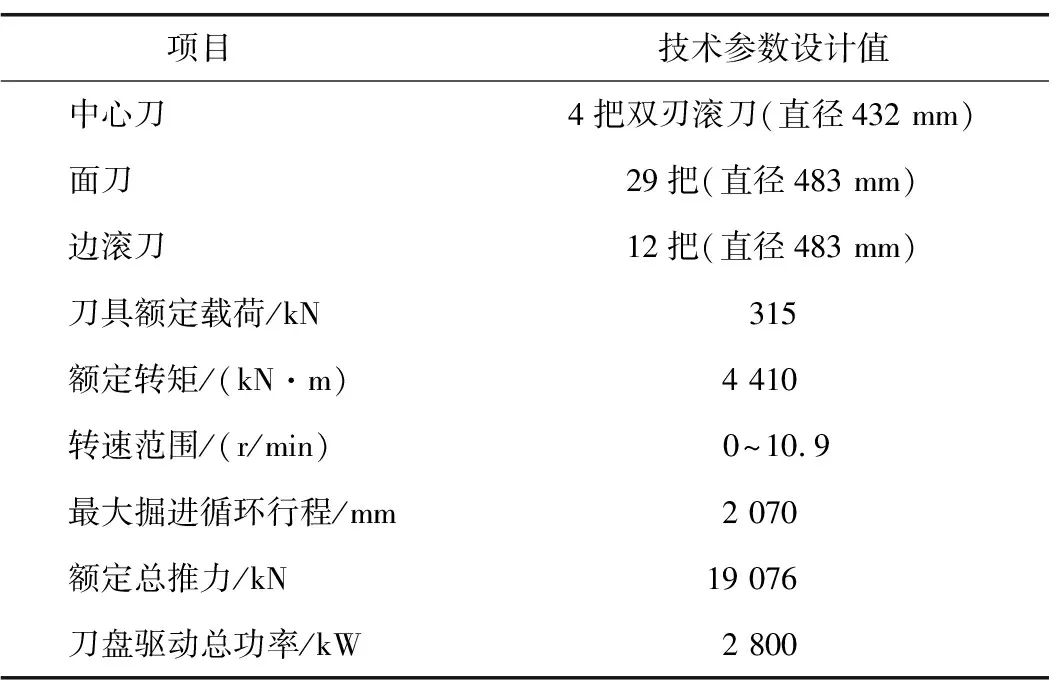
表1 TBM主要技术参数
1.2 不同围岩的TBM掘进性能对比
依照传统BQ法,本标段围岩等级分为Ⅱ、Ⅲ、Ⅳ、Ⅴ类,且在Ⅲ类围岩基础上可再细分为ⅢA与ⅢB。TBM围岩大多数集中在Ⅲ类围岩,Ⅴ类围岩较少。选取里程桩号为57+797.4~53+927.9的典型洞段进行数据采集和统计分析。对BQ法定义的不同围岩下的TBM掘进性能进行统计分析,找到影响围岩可掘性分级的掘进性能指标。
1.2.1 不同围岩的TBM净掘进速度、贯入度与转速
不同围岩的TBM平均净掘进速度、平均贯入度与平均转速分别见图1(a)—(c)。

(a) 不同围岩TBM平均净掘进速度

(b) 不同围岩TBM平均贯入度

(c) 不同围岩TBM平均转速
Fig. 1 TBM average net driving speed, penetration and rotation speed in different surrounding rocks
TBM在ⅢB围岩下净掘进速度最高,在Ⅱ围岩下净掘进速度最低, Ⅲ、Ⅳ围岩下净掘进速度相差不多。
1.2.2 不同围岩下TBM掘进作业利用率
TBM掘进作业利用率是指掘进时间占总施工时间(包括: 掘进、换步、支护、故障以及其他原因造成的停机时间)的比例。基于现场大数据分析,不同围岩下TBM掘进作业利用率见图2。

图2 不同围岩TBM掘进作业利用率
TBM在Ⅱ类围岩下掘进作业利用率最高,在Ⅳ类围岩下掘进作业利用率最低。Ⅱ类围岩相对较为完整,不需要打锚杆、立拱架等,减少了支护工作对掘进的延误,所以掘进作业利用率比较高,而本文所研究洞段地质条件以Ⅲ类围岩为主,大量支护工作延误TBM掘进。
1.2.3 不同围岩下TBM施工速度
综合考虑TBM维护、支护工作等停机因素影响,TBM在不同围岩下平均施工速度见图3。

图3 不同围岩TBM平均施工速度
Fig. 3 TBM average construction speed in different surrounding rocks
TBM在Ⅱ类围岩下不用大量的支护工作,平均施工速度最快,其最高日进尺为59 m。
1.2.4 不同围岩下TBM可掘性指标FPI与TPI


(a) 不同围岩FPI对比

(b) 不同围岩TPI对比
由图4可见,不同围岩的FPI、TPI具有非常明显的区分度,Ⅱ类围岩FPI、TPI值最高,表明TBM贯入度为1 mm/r时所需的单刀推力以及刀盘转矩最大,ⅢA与ⅢB次之,Ⅳ围岩最小。
综合分析不同围岩条件下TBM的掘进性能,净掘进速度、掘进作业利用率、施工速度、FPI与TPI在不同围岩下具有的明显区分度,可以作为表征围岩可掘性的指标。若以净掘进速度为分类标准,则ⅢB类围岩为最佳掘进围岩,但其掘进作业利用率较低,围岩完整性较差,容易发生塌陷、卡机等事故,施工风险较高,并且施工速度较低,TBM适应性一般,故净掘进速度不宜作为围岩可掘性分级指标。由此选定掘进作业利用率、施工速度结合FPI与TPI为TBM围岩可掘性分类指标。
1.3 围岩可掘性分级
在实际施工中发现某些完整性较好的ⅢA围岩,其可掘性与Ⅱ类围岩相近,见表2。
表2 特殊ⅢA类与Ⅱ类围岩掘进参数均值对比
Table 2 Comparison of average value of driving parameters between special Grade ⅢAand Ⅱ surrounding rocks

围岩类别转速/(r/min)贯入度/(mm/r)FPI/(kN/(mm/r))TPI/(kN·m/(mm/r))净掘进速度/(mm/min)施工速度/(m/h)ⅢA类Ⅱ类7.08.02634356.01.347.08.12638856.71.36………………7.08.42632958.81.417.08.12734856.71.366.97.93033756.11.38
由表2可知,在某些完整性较好的ⅢA类围岩下TBM适应性与其在Ⅱ类围岩下基本相当,且并不需要打锚杆、立拱架等支护工作。该ⅢA类围岩可掘性指数集中在一定的范围,其FPI>25 kN/(mm/r)、TPI>320 kN·m/(mm/r)。
传统BQ法定义的Ⅱ类围岩完整性较好,不需打锚杆、立拱架等支护工作,施工风险较低。在Ⅱ类围岩下TBM掘进作业利用率与施工速度均为最高。尽管在实际过程中某段Ⅱ类围岩单轴抗压强度较大,但TBM设计之初对掘进参数都保留较大的空间,所以TBM在较硬的Ⅱ类围岩也可以达到较大的贯入度,刀具磨损虽然有所增大,但与快速掘进所带来的的效益相比不显著,其TBM适应性最好。
传统BQ法定义的ⅢA与ⅢB类围岩下, TBM施工速度与掘进作业利用率次于Ⅱ类围岩,且FPI<25 kN/(mm/r)、 TPI<320 kN·m/(mm/r)的ⅢA与ⅢB类围岩大多完整性较差,施工风险高于Ⅱ类围岩。考虑到ⅢA与ⅢB围岩岩性相同,故可将其归为同一类围岩,此类围岩TBM适应性一般。
传统BQ法定义的Ⅳ与Ⅴ类围岩由于大多较为破碎,完整性很差,容易发生塌方、卡机等事故,施工风险较高。虽然TBM可以通过增大推力等掘进参数获得较大的贯入度和净掘进速度,但是实际掘进过程中考虑到施工安全以及支护困难,往往在Ⅳ类围岩会主动降低掘进参数,达到一个较低的贯入度,减少对围岩的扰动,并增加钢筋排等支护,其掘进作业利用率与施工速度均为最低。TBM对Ⅳ类与Ⅴ类围岩的适应性最差。
综合以上分析,将传统BQ法确定的Ⅱ、ⅢA、ⅢB、Ⅳ类围岩依据TBM掘进性能与施工风险进行可掘性分级,将FPI>25 kN/(mm/r), TPI>320 kN·m/(mm/r)的ⅢA类围岩以及Ⅱ类围岩的围岩可掘性等级定为A类;将FPI<25 kN/(mm/r)、TPI<320 kN·m/(mm/r)的ⅢA类与ⅢB类围岩定为B类;将Ⅳ类与Ⅴ类围岩定为C类, 如表3所示。
表3 基于TBM适应性的围岩可掘性分级
Table 3 Grade of surrounding rock excavatability based on TBM performance

围岩可掘性等级判别依据TBM适应性评价A 传统Ⅱ类与FPI>25 kN/(mm/r),TPI>320 kN·m/(mm/r)的ⅢA类围岩良B FPI<25 kN/(mm/r), TPI<320 kN·m/(mm/r)的ⅢA类与ⅢB类围岩中C传统Ⅳ类与Ⅴ类围岩差
传统BQ法认为Ⅲ类围岩可掘性最好,通过对本标段TBM掘进性能与施工风险分析得出Ⅱ类围岩可掘性要优于Ⅲ类围岩,且某些特殊的ⅢA类围岩的可掘性与Ⅱ类围岩的可掘性相当,应将其与Ⅱ类围岩归为一类。
基于TBM掘进性能与施工风险得出的围岩可掘性分级方法,对传统BQ法定义的围岩进行重新分级。在传统BQ法基础上,结合反映TBM掘进围岩特征参数指标FPI、TPI来对围岩进行分级,更加符合TBM实际施工特点,并且弥补了BQ法在现场某些完整性较好的ⅢA类围岩下应用的局限性。
2 围岩可掘性等级实时识别方法理论与算法
2.1 主成分分析
主成分分析(PCA)是一种传统统计分析方法,可以将多个指标转换为少数几个综合指标,由霍特林于1933年首次提出。PCA主要适用于处理维度较高且各个变量之间的相关性较好的数据。其数学原理是将原始的P个变量作线性组合成为新的变量。从数学的角度看,求解主成分其实就是根据数据源的协方差矩阵求解特征根、特征向量的过程。主成分可以利用协方差阵特征值对应的单位正交特征向量来表示。协方差矩阵与原始变量的线性组合即为主成分,见式(1)。
(1)
式中:Y为各主成分;μ为协方差矩阵的各个元素;X为原始变量相应的值。
由式(1)可知,有几个原始变量,就会得到几个主成分。实际工作中,通常只挑选前几个方差最大的主成分,从而达到简化系统结构、抓住问题实质的目的。而根据协方差矩阵的特征根便可以选择合适的主成分,这里引入贡献率的概念,见式(2)。
(2)
式中:λ为协方差矩阵特征根;Pk为第k个主成分的贡献率,一般取前m个主成分的贡献率之和(累积贡献率)大于85%。
前m个主成分Y1、Y2、…、Ym便是经过主成分分析之后所得的主成分,一般m 人工神经网络起源于20世纪50年代,神经网络是一种模仿生物神经元的数学模型。大多数情况下,神经网络可以根据外部信息输入改变内部基础结构,实现接近期望的输出,如图5所示。 BP(back propagation)神经网络是一种多层前向网络,又叫多层感知器,是人工神经网络的精华,广泛应用于回归、分类、预测等领域中。现在大约80%的神经网络都是在BP神经网络的基础上构建的。BP神经网络基于误差反向传播算法对输入进行训练学习,主要结构分为输入层、隐含层、输出层3层。 有时为了提高BP神经网络的准确性会增加隐含层层数以及隐含层节点数,但这样会使模型趋于复杂化,降低模型的响应速度,且容易使模型过拟合。对于一般的非线性问题,隐含层层数设定为1层,最佳隐含层节点数可参考式(3)。 (3) 式中:l为隐含层节点数;n为输入层节点数;m为输出层节点数;a为0~10之间的常数。 (a) 生物神经元模型 (b) 人工神经网络 BP神经网络输入层经过权重计算传到隐含层,隐含层再经过一次权重调整到达输出层,得到的数值与期望数值计算误差之后反向传播回输入层,模型根据误差不断调整权重直到误差达到初始目标设定值便停止迭代,具体原理见图6。 图6 BP神经网络原理 为了克服传统统计方法的局限性,有效地应用BP神经网络强大的非线性分类能力,本文采用PCA与BP神经网络相结合的方法对围岩可掘性等级进行实时识别。由PCA对原始数据进行处理后得到相应的主成分,将主成分作为BP神经网络的输入层建立模型。该方法不仅能够保留原始数据的大部分信息,而且经过PCA处理过的数据维度降低,简化了模型,提高了模型的响应速度。张国英等[13]对比该方法与传统BP神经网络法的准确性发现,由该方法得到的模型准确性比传统BP神经网络更高。 3.1.1 不同围岩等级下TBM掘进参数均值统计 表4 不同等级围岩TBM掘进参数均值 Table 4 Average TBM driving parameters in different grades of surrounding rocks 围岩可掘性等级刀盘转矩/(kN·m)刀盘推力/kN刀盘转速/(r/min)贯入度/(mm/r)FPI/(kN/(mm/r))TPI/(kN·m/(mm/r))A2 45610 1656.997.9730.9337B1 9737 8786.718.8819.7233C1 5166 1826.569.1314.7170 由表4可以看出,随着围岩可掘性等级的不断下降,各掘进参数有着非常明显的变化,区分度较高。在此基础上可以判断TBM各掘进参数与围岩可掘性等级必然具有某种关系。许多学者研究过上述各掘进参数与围岩类别之间的相关关系以及各掘进参数之间的相关关系[15],表4所列各个掘进参数在TBM主操控室可以获取,且FPI与TPI在TBM领域也应用较为广泛,可通过简单编程计算得到。故选择此6个掘进参数作为围岩可掘性等级识别的基础指标。 3.1.2 各掘进参数之间的相关性分析 由主成分分析数学原理可知,在对各掘进参数进行主成分分析之前必须对其进行相关性分析。此前已有许多学者对表4所述各掘进参数的相关性进行研究[15],这里只验证各掘进参数是否具有相关性即可。选取各围岩等级下的典型掘进数据共240组,其中,A类围岩60组,由于B类为施工常见围岩故选取120组,C类围岩60组。各等级围岩原始掘进数据见表5。 表5 各等级围岩原始掘进数据 Table 5 Original excavation data under different grades of surrounding rocks 围岩可掘性等级刀盘转矩/(kN·m)刀盘推力/kN刀盘转速/(r/min)贯入度/(mm/r)FPI/(kN/(mm/r))TPI/(kN·m/(mm/r))ABC2 45011 37675.840.04222 93010 74978.226.7357………………1 9708 49677.124.42772 2209 00079.718.9228………………1 2005 21269.111.61311 6305 421612.29.06133……………… 运用SPSS软件对表5各掘进参数进行相关性分析,得其相关性矩阵见表6。 表6 各掘进参数相关性 由表6可知各掘进参数具有显著的相关性,适合做主成分分析。 3.2.1 数据预处理 为了消除各掘进参数不同量纲影响,避免绝对值较大或较小的数据干扰分析结果,对原始数据进行标准化处理,见式(4)。 肘部骨折在所有儿童骨折发生率中都占了很大比例,据统计约占30%,而其中又以肱骨髁上骨折最为常见占了50%-70%[1,2]。一般通过闭合复位经皮克氏针内固定方法治疗,临床上也取得了不错的疗效,但同时也因为这类肱骨髁上骨折的不规则和偶伴有血管神经损伤,这对闭合复位的治疗增加了更不确定和操作复杂度,同时患儿在术中术后都面临了更多的风险,近年临床开始选择小切口辅助复位经皮克氏针固定法治疗,取得一定效果[3]。现就我院在2014年12月-2018年12月期间收治的100例儿童肱骨髁上骨折患儿为观察对象,分别进行小切口辅助复位与闭合复位治疗,比较其临床治疗效果,旨在为临床研究提供有价值依据,报道如下。 (4) 3.2.2 标准化数据主成分分析 运用SPSS软件对标准化数据进行主成分分析,各主成分特征值及累积贡献率见表7。 表7 各主成分特征值及累积贡献率 Table 7 Characteristic root and cumulative contribution rate of each main component 主成分特征值方差百分比/%累积贡献率/%14.32071.99471.99421.22020.33692.33030.3305.50797.83840.0781.29899.13550.0500.84199.97660.0010.024100.000 由表7选取特征值在1以上,累积贡献率85%以上的主成分,提取第1主成分与第2主成分。前2个主成分对原始变量信息的提取率见表8。 表8 各主成分对原始数据提取率 由表8可知,第1主成分和第2主成分基本提取了原始数据的大部分信息。第1主成分主要与刀盘转矩、刀盘推力、刀盘转速、FPI、TPI有关;第2主成分主要与贯入度有关。经过主成分分析后得到各主成分的成分得分系数,见表9。 表9 各主成分的成分得分系数 Table 9 Component score coefficient of each principal component 掘进参数主成分F1主成分F2刀盘转矩/(kN·m)0.1960.378刀盘推力/ kN0.2580.087刀盘转速/(r/min)0.1740.327贯入度/(mm/r)-0.1220.512FPI/(kN/(mm/r))0.240-0.270TPI/(kN/(mm/r))0.261-0.099 将各主成分得分系数与标准化原始数据值线性组合后得到各主成分得分的具体值,见表10。 表10 各主成分得分 在构建BP神经网络模型之前对240组主成分F1与F2运用MATLAB归一化函数进行归一化处理,所有主成分数值归一化到[-1,1]。将归一化之后所得的240组主成分F1、F2随机排序并作为输入层运用MATLAB软件构建一个3层BP神经网络。随机选择其中10组A类、20组B类、10组C类共40组作为测试数据来验证模型的训练性能,剩余200组数据作为训练数据。经过不断调试并避免过拟合现象之后,选定输入层为2,隐含层为7,输出层为3,见图7。 图7 PCA-BP神经网络模型 在经过300次迭代后,模型收敛,达到目标要求的误差,见图8。 图8 PCA-BP神经网络模型训练误差 具体测试数据与识别结果见表11。其对40组选取的测试数据识别率达到100%。在此需要说明,并非模型的准确性达到100%,而是在调试的过程中,不断调整隐含层节点数以及训练次数,以求使模型对40组测试数据的识别率达到最高,这时所得到的模型为基于240组原始数据所能达到的最佳模型。由此可知,模型在经过不断调整之后其训练效果已达到目标要求。 按照从原始数据到围岩可掘性等级识别结果,这一系列对围岩可掘性等级进行判断的操作,耗时较长,且在施工中存在跟不上TBM掘进速度的问题,不能实时识别,应用具有局限性。为了提高模型对原始数据的响应速度,本文对所构建的PCA-BP神经网络模型进行改进。 将在SPSS软件中对原始数据标准化与主成分分析之后所得主成分F1和F2 2个步骤运用MATLAB编写一个程序,该程序可以对原始数据标准化并根据在SPSS软件中主成分分析之后所得主成分得分矩阵计算主成分F1和F2。同时,调用函数对之前已训练好的神经网络模型进行仿真。这样整个模型只需输入原始掘进参数便可以快速识别围岩可掘性等级,见图9。 表11 PCA-BP神经网络对围岩类别识别结果 注: 训练结果显示,A类围岩为[1,0,0],B类围岩为[0,1,0],C类围岩为[0,0,1]。 由图9可见,改进后的模型只需在命令窗口输入原始数据便可得到围岩识别结果,并且经过多次测试,其响应速度不到1 s。而且, 如果一次数据量较多,可以将其原始数据放到一个内存很小的TXT文件中,并在命令窗口调用, 便可以得到识别结果。经过测试,其响应速度会随着数据量的增加而减小,但考虑到TBM在施工中,每min存储1组数据的特点,该模型的响应速度仍然远远超过TBM的数据采集速度,符合实际施工要求。 PCA-BP神经网络模型虽然在训练过程及测试过程中表现良好,但其在实际应用过程中的准确性是否能够满足要求,还需进一步进行可靠性检验。 图9 基于MATLAB的围岩识别快速响应模型 Fig. 9 Rapid response model for surrounding rock discriminate based on MATLAB 由于本文研究所采取的数据为新疆EH隧道工程KS Ⅳ标段上游TBM 2,该标段采用“一洞双机”施工方案,为了检验模型可靠性,选择下游TBM 3进行模型验证。现场进行测试时,采集A、B、C类围岩各10组,共30组掘进数据进行模型仿真,结果对比见表12。 由测试结果可知,B类、C类围岩各有1组数据预测错误,整体准确率为93.3%。该模型在该工程中适用性较好。 表12 新疆EH工程模型检验 1)在凝灰岩条件下,给出了传统BQ法围岩分类结合FPI、TPI指数的TBM施工围岩可掘性分级方法。该方法在新疆EH工程中应用效果较好,可为后续类似工程TBM施工围岩分级提供参考。 2)通过主成分分析与BP神经网络相结合的方法,建立了围岩可掘性等级识别模型。经过在本工程另一标段检验证明,该模型准确率较高。 3)针对围岩等级分类实时识别,设计了一个MATLAB程序,极大地提高了模型对围岩可掘性等级识别的响应速度,满足实际施工要求,且增强了该模型在TBM应用中的人机交互体验,为后续类似的围岩可掘性实时识别软件开发与TBM应用相结合提供借鉴。 PCA-BP神经网络的方法对围岩可掘性等级进行实时识别所得到的数据、关系、研究方法对TBM围岩可掘性实时识别、主参数设置以及智能化掘进都具有参考价值。若能在此基础上对不同TBM、不同岩性的工程案例进行类似研究,通过不断积累深化,则可以得到更加通用的围岩可掘性实时识别模型。2.2 BP神经网络
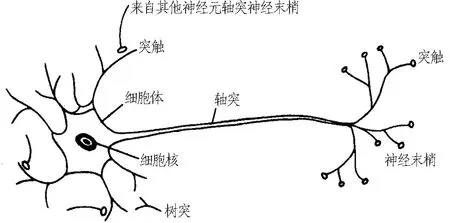


2.3 PCA+BP神经网络
3 TBM围岩可掘性等级实时识别模型建立
3.1 不同围岩下TBM掘进参数统计与相关性分析
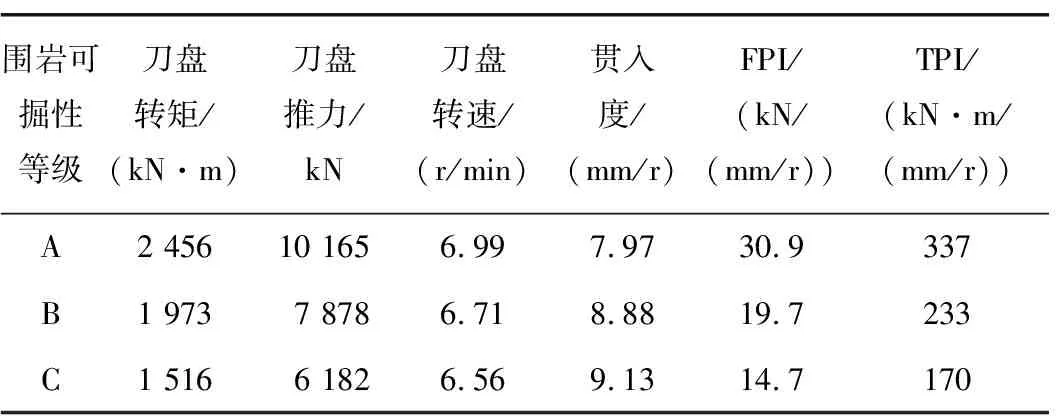


3.2 TBM掘进参数主成分分析





3.3 PCA与BP神经网络联合建模


3.4 PCA-BP围岩识别模型快速响应改进方法

4 PCA-BP神经网络模型可靠性检验


5 结论与讨论

