复杂网络视角下的金融市场结构演化与风险传染

游鸽 郭昊 刘向

摘   要：以“复杂网络”为视角，将金融市场抽象为多主体在时间与结构上无限延展关联的复杂系统，有助于厘清金融市场宏观整体与微观主体之间的相互作用，有效研判金融市场的发展趋势，对预测系统性金融风险的产生有重要意义。本文从拓扑结构、演化机制与风险传染机制三个方面综述了金融市场网络研究的进展，从金融市场网络的结构特征与演化机制两个方面，总结了金融市场网络结构的演化，从金融市场网络结构对系统性金融风险的影响以及金融风险传染模型方面，总结了金融市场网络的风险传染，并基于当前研究的不足指出未来的研究趋势。

关键词：金融市场;复杂网络;演化;系统性风险;风险传染

中图分类号：F830  文献标识码：A  文章编号：1674-2265（2020）01-0030-10

随着现代金融业的不断发展，金融市场参与主体日益增多，逐步演化为政府、金融机构、企业组织与个人等多主体参与形成的，在时间与结构上无限延展关联的复杂系统。如果将系统中各主体抽象为网络节点，各主体之间的相互作用抽象为节点之间的连接线或边，那么整个系统就可以抽象为多重节点关联的复杂网络。面对如此庞杂的金融网络系统，要想对其发展趋势做出准确的判断已变得异常困难。传统金融学理论基于超理想化、形式主义化、线性单一化假设的方法与现实金融系统的复杂性相互冲突，因此，其难以有效地预测金融危机的发生与系统性金融风险的影响。金融市场这种复杂性已使得传统金融理论遇到了难以逾越的障碍，张卫国（2017）形象地将其称为“新金融经济学发展难以突破的瓶颈”。而利用复杂网络的方法来研究金融市场网络的拓扑结构及演化过程为解决这一难题提供了一种全新的研究思路。

早在20世纪90年代，学者们即开始探索利用复杂网络的方法对金融市场的结构进行统计描述。例如Angelini等（1996）对意大利网络系统中“多米诺骨牌效应”的潜在规模进行了实证评估，模拟结果显示，4%的参与者结算失败就足以引发系统性危机。Boss等（2004）基于实证分析，发现银行间网络遵循双幂律度分布。Mouss（2011）对巴西金融机构网络结构进行了实证分析，发现该网络是明显的无标度网络，而不是小世界网络。Cont（2013）实证统计的结果延续了Mouss的发现，并强调异质性在网络结构中的贡献以及对特定机构的交易对手风险集中度在解释其系统重要性时的作用。Gai等（2011）构建了由24家英国银行组成的银行间拆借网络，网络统计结果显示，其中5家大型银行具有较高的网络中心度，处于网络的核心，剩下中小型银行处于网络的外围，且不直接相连。Solorzano等（2013）根据2008年7月至2010年12月的每月风险暴露数据，构造了包括银行、金融中介在内的墨西哥金融网络，统计结果显示，网络结构与随机网络相近，且呈现层次性特征。陈少炜等（2016）绘制了我国银行网络的结构图，结果显示我国银行网络是一个拥有少数货币中心的三层结构特征网络，并呈现出明显的无标度特征。

基于上述实证统计的结果，部分学者开始探索使用数理模型来描述金融市场网络的结构演化与风险传染机制。例如Wan等（2006）基于实证统计分析的结果，提出了一个银行网络结构生成模型来解释银行网络双幂律度分布形成的机制。范宏等（2014）建立带有宏观经济趋势及多期清算的动态银行网络系统模型，提出了一种系统性风险的定量计算方法，仿真实验得到的变化曲线有效地表现了系统性风险的累积过程。Aleksiejuk等（2001）引入了一种新的定向渗流模型，作为银行系统中传染过程和大规模破产的简单表示，用随机分布有向连接模拟模型中的货币流，模拟结果解释了美国大萧条期间由于少数银行破产引发大规模银行破产的现象。Allen等（2000）指出一个地区的小流动性偏好冲击可能会在整个经济中蔓延，蔓延的可能性很大程度取决于区域银行间索赔结构的完整性，完整的银行间索赔结构比不完整的结构更能抵御系统性风险的冲击。Ladley等（2013）提出了一个封闭经济的局部均衡模型，其中银行的行为和银行间利率确定是内生的，仿真结果表明银行行为的内生特征和银行间市场行为与现实中观察到的特征非常吻合。贾彦东（2011）基于金融网络风险扩散模型重点研究了金融机构间的风险分担模式，结果显示金融机构对整个系统的影响主要来自“直接贡献”和“间接参与”两个方面。陈建新等（2012）基于集合种群理论构建了银行风险传染模型，利用元细胞自动机方法对银行风险传染进行模拟分析，提出了脆弱性传染的影响因素。

研究金融市场网络结构及演化机制是探索金融市场发展趋势的基础，是捕获金融风险的有效手段。尽管很多文献对金融市场网络拓扑结构及演化过程进行了研究，然而分散在不同的学科、研究团队以及期刊上，因此关于金融网络的研究，现在还没有清晰的图景。虽然一些早期的文献综述涵盖了大量的研究，但是它们没有基于某一研究宗旨来系统地汇总这些知识。因此，本文采用文献梳理与系统分析的方法，围绕防范系统性风险这一研究宗旨，深入探讨金融市场网络的结构与演化，分析当前研究的不足，并指出未来研究的重点。

一、基本概念与理论

（一）金融市场网络的概念

金融市场是由货币市场、外汇市场、证券市场等多个子市场组成，并由金融机构、政府、企业组织与个人等多主体参与，在时间与空间上不断演化形成的复杂系统（如图1a所示）。在复杂网络的视角下，本文将金融各子市场参与主体之间的复杂性关联结构定义为金融市场网络，因此，按照金融子市场间的差异，金融市场可以抽象为银行间市场网络、股票市场网络、外汇市场网络等多个子网络相互关联的复杂网络结构（如图1b所示）。金融市场网络是一个集合概念，指的是金融市场参与主体之间相互关联的一类网络。在金融市场网络中，节点一般代表政府、金融机构、企业组织与个人等金融市场参与主体;边即表示金融市场参与主体间的连接关系。具體而言，在银行间市场网络中，边即是银行之间的同业拆借关系;在外汇市场网络中，边是指各国货币之间汇率波动的相关关系;在股票市场网络中，边是指企业股票之间的相关关系;而在证券文本网络中，边即是证券公司之间文本信息之间的交互关系。

金融市场网络中新节点的加入，可理解为金融市场新主体的参与，金融市场网络中各个节点之间的连接发生变更，可以理解为金融主体之间的关联发生了改变。具体而言，例如银行间网络中，由于银行间拆借关系的更新变动，网络中节点间连接可以变化与重连（如图2c所示）;股票市场网络在时间的维度不断有企业股票上市与退市，映射到网络结构上，就是整个网络随着时间的演化不断地有新节点进入与旧节点退出，所以股票市场网络是无环的有向网络（如图2d所示）。

将网络中边的方向去除则是无向网络;给连接边赋权，则为加权网络;假设节点状态与网络为动态演化的，则是动态网络。目前针对金融市场网络的研究多基于无向网络，较少考虑动态性、方向性、权重以及节点的异质性。然而动态网络、有向网络、加权网络、二分网络更接近金融市场网络演化的实际（见图3），例如在银行—企业信贷网络中，整个网络是由银行与企业两种不同性质的节点组成，是典型的二分网络，并且该网络在时间标度上存在明显的动态性，网络中各企业银行之间连接强度的差异，使得整个网络连接权重不一致，有明显的加权网络特征。因此，在金融市场网络演化过程中，将有向性、加权性、动态性、二分性或多元性考虑进去要更加贴近实际，未来应对这几个方面进行着重研究。

（二）理论来源与发展思路

对金融市场网络结构的研究源于复杂网络的研究框架。1998年Wattz和Strogatz提出的著名的小世界网络以及1999年Barabási和Albert提出的无标度网络为金融市场网络的研究提供了理论与方法。之后关于金融市场网络结构实证统计与演化模型的研究开始逐渐兴起。

Boss等（2004）、Souma等（2012）、Soramaki等（2007）立足于金融市场网络的实证统计分析，运用数理统计的方法对金融市场网络的网络密度、平均路径长度、聚类系数、度分布（有向网络包括入度分布与出度分布）等指标进行统计分析，用以描述现实金融网络的拓扑结构特征。他们的工作开创了金融网络实证统计的先河。目前针对不同金融市场网络的实证统计研究取得了较大的进展，其中较具代表性的研究梳理如下：（1）对银行市场间网络的实证统计分析，除Boss、Souma、Soramaki作出的贡献外，Becher等（2008）对英国各银行清算自动支付系统网络进行了实证统计，结果显示其具有较低的连接度与平均路径。Santos等（2010）通过实证研究发现巴西银行间网络的度分布服从幂律分布。（2）对银行—企业间网络的实证统计分析，Miranda等（2013）实证统计得出巴西公司—银行贷款网络的度分布遵循幂律分布。De Masi等（2011）统计发现由公司和银行构建的日本信用网络服从厚尾分布。（3）对股票市场网络的统计分析，Lee等（2007）利用韩国股票市场中股票价格的互相关系构建了股票市场的关联网络，统计发现其度分布遵循幂律分布，且幂指数取决于相关系数的阈值。张来军等（2014）构建收益率、成交量、市盈率的股票关联网络，统计发现股票收益率和成交量指标具有较强的关联性，且具有小世界性;市盈率指标关联性较弱，不具有小世界性。

另一种思路立足于模型的构建，基于这一思路的研究多聚焦于对金融市场网络结构演化模型与风险传染模型的研究，代表性的研究有以下几种。（1）关于金融市场网络结构演化模型的研究，万阳松等（2007）提出了一个银行间网络结构演化模型，以此解释银行间网络双幂律分布形成的机制。Li等（2010）基于银行间的信贷关系构建了银行间市场的网络增长模型，该模型可以较好地表征现实世界中银行间市場网络中无标度结构特征。（2）关于金融风险传染模型的研究，Thurner等（2003）结合银行间的风险传染问题构建了基于风险共担的银行合作网络动态博弈模型。Xu等（2016）提出了一种基于银行代理行为的动态银行间市场网络模型，用于分析交易对手和流动性渠道的金融风险传染。Jiang等（2018）提出了一种基于信息非对称关联的信用风险传染模型，该模型能够有效地反映个体间信用风险的传染程度。

上述两种思路各有优势，前者针对大规模网络实证分析具有优势，便于从真实数据统计的角度定性地描述金融市场网络的拓扑结构特征;后一思路从微观的视角分析网络结构中节点间作用机制、关联规则以及网络演化规律，用数学模型来描述网络的结构生成与传染，虽然能更好刻画金融市场中各个主要参与主体的活动与演化过程，但由于金融市场的多主体性与复杂性，根据这一思路研究金融网络演化模型较为困难。随后对金融市场网络结构和演化的研究基本上延续了这些差异。

二、金融市场网络的结构

（一）不均匀性

不均匀性是金融市场网络的一般拓扑结构特征。Boss、Souma、Soramaki、Becher、Santos等人较早开始了银行间市场网络的实证统计研究，发现其度分布服从幂律分布，呈现无标度特征。此外，Liu等（2012）、Cao等（2017）、刘海飞等（2018）实证统计发现股票市场网络呈现无标度特征。庄新田等（2007）对上海证券市场网络进行了统计分析，发现该网络度分布服从幂律分布。秦春雷等（2015）分别对金融危机前、中、后期的证券市场网络结构变化做了统计，结果表明前期网络聚类系数、平均度上升至较高水平，中期则基本持平波动较小，后期下降并停留在比前期高的水平。此外，王莹等（2018）从多频视角分析了由全球45种主要货币组成的外汇市场的网络结构，研究发现外汇市场网络呈现无标度特征。

上述针对银行间市场、股票市场、证券市场、外汇市场等金融子市场网络的实证统计发现它们表现出一个共同特征，即无标度特征，网络中一些节点连接度较高，而其他大量的节点具有较低连接度，在宏观上呈现出“富者更富”的马太效应，体现了网络极大的不均匀性。关于无标度网络的应用研究，黄玮强等（2008）利用上证与深证指数分别构建了沪深市场的无标度网络模型。李进等（2009）基于上市公司之间交叉持股关系构建了利己连接规则的无标度网络。

（二）小世界结构

小世界特征是金融市场网络另一重要的拓扑结构特征。Vivier-Lirimont（2004）通过银行间关系网络分析了银行间借贷模型，然后解释了自20世纪80年代金融自由化进程开始以来银行网络的密集化，这为金融市场网络小世界现象奠定了理论基础。之后Boss、Soramaki等（2010）陆续发现银行间市场网络的小世界性。Bech等人通过美国联邦基金市场网络的拓扑结构进行统计分析，发现基金市场的小世界现象。Gao等（2013）利用滑动窗口技术对动态的股票市场网络进行统计分析，结果表明，随着时间的推移，股票市场网络具有强大的小世界属性。此外，国内学者张骥等（2017）实证统计发现2015年股灾背景下的中国证券市场网络结构具有明显的小世界性。韩东梅等（2014）统计发现国际证券市场的网络具有显著的小世界性。

上述文献表明金融市场网络普遍存在小世界现象，小世界原理是金融市场网络中各主体之间紧密关联的具体表现，高聚类系数和短平均路径实现了金融大世界向小世界的转换，而小世界网络模型不仅很好地描述了金融市场网络内部密切的关联性，也为金融市场小世界网络的结构生成提供了实现方式。关于小世界网络的应用性研究，Chen等（2007）利用多主体仿真技术开发了Watts-Strogatz网络仿真模型，指出该仿真模型有望在未来分析金融市场中小世界资产现象时呈现较好的效果。李旲等（2012）利用小世界网络模拟金融市场全局信息下的投资人基于社会网络的决策机制。

三、金融市场网络的演化

（一）无标度特征的生成机制

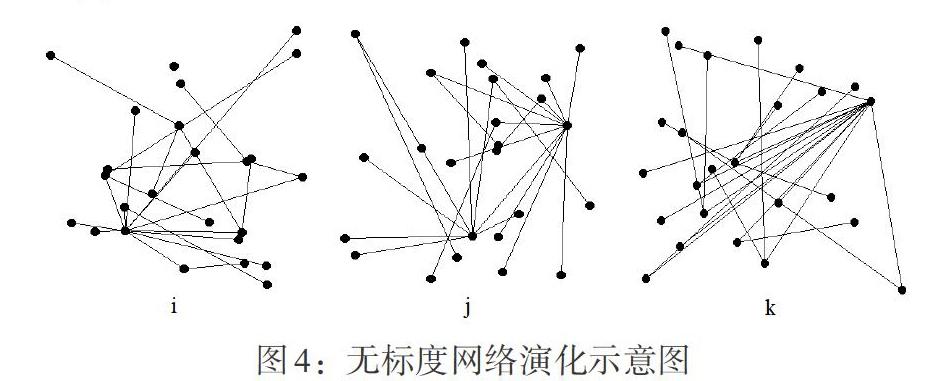
近年来，金融市场网络结构特征的实证研究发现银行间市场网络、股票市场网络、证券市场网络等都具有明显的无标度特征。1999年无标度网络模型（BA模型）被提出，其构造算法如下：（1）增长，初始网络存在m0个节点，且节点的度之和为kmo。（2）择优连接，以概率p将新节点与一个已存节点i相连，连接的概率Π（i）与节点i的度ki成正比（度择优连接），故其择优连接概率Π（i）= ki /Σ kj，故在t时间步，它的连接度变化率为：?ki/?t=xki/Σkj，求解得到P（k）∝2m2k-3。这表明其度分布是接近幂率为3的分布。利用Matlab构建初始网络节点为4，每次加入一个节点，以连接概率p与其中一个节点相连，设置时间步t=25，最终得到节點数为25的网络图（见图4，其中图4i中p=0.1，图4j中p=0.3，图4k中p=0.5）。

BA网络及其改进模型虽然有效地刻画了金融市场网络的内部结构特征及其演化规律，但是实际金融市场中由于参与主体间连接更趋复杂，使得真实网络演化过程与BA模型存在差异。表现在：BA网络是基于度择优连接规则构建的网络，从而使得其在宏观上呈现出“马太效应”，然而真实的金融市场网络节点更偏好于适应度较好的节点连接，也就是说一个金融机构更愿意与稳健性好、抗风险能力强的金融机构产生关联。因此，真实的金融市场网络结构与演化要比BA无标度网络更趋复杂性。

（二）小世界结构的演化机理

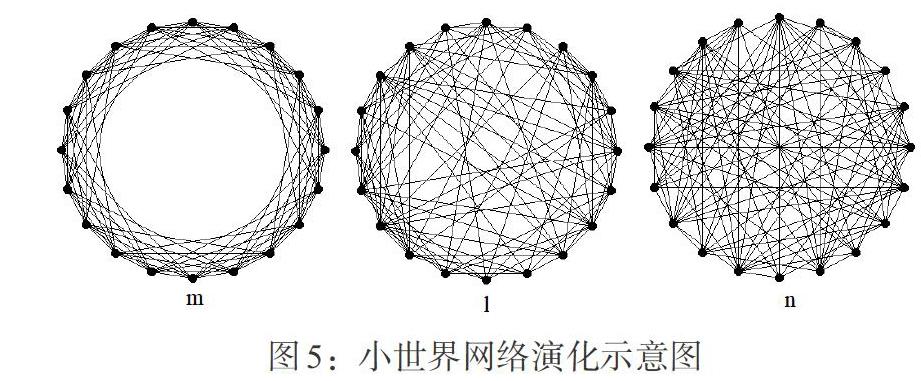
小世界网络结构阐述了金融市场中各参与主体间关联的紧密性，小世界网络模型（WS模型）构造算法如下：（1）规则网络。一个最近邻耦合环形网络有N个节点，每个节点都跟它左右相邻各K/2节点相连（K为偶数）。（2）随机重连。以概率p随机重连网络中的每条边，其中，每个节点不能与自身相连，任意两个节点间至多能有一条边，由此而形成的低平均路径长度、高聚类系数的网络即为小世界网络。运用Matlab构建网络节点数为20，随机重连概率为p，最终得到节点数为20的网络图（见图5，图5m中p=0.1，图5l中p=0.5，图5n中p=1）。

WS模型虽然很好地描述了小世界网络的规则性与随机性，但该模型借助断边与随机重连来构造网络易破坏网络的连通性。为了解决这一问题，Newman 和Wattz（1999）提出了NW小世界网络模型，利用随机加边来构造小世界网络，很好地解决了因为连接边的断连致使连通性破坏的问题。之后Newman还提出了其他的小世界改进模型。

上述小世界网络构造模型及其改进模型虽然有效地描述了金融市场网络较低平均路径长度与较高聚类系数的特性，但是其与实际金融市场网络的演化过程存在很大的差异，主要涉及如下两点：（1）金融市场网络是一个在时间标度上节点与连接边动态增长的网络，银行市场网络、股票市场网络与外汇市场网络都是如此，而上述模型都是在既定节点数的规则网络上构建的，没有考虑节点的增长。（2）金融市场网络中边的连接一般围绕特定的资本市场或者区域，进入市场的新的主体通常会连接特定资本市场的或者区域的旧主体，而并不是如WS、NW模型中简单的随机连接一般。

（三）演化模型

考虑金融市场网络节点连接数增长的特征，Philippas等（2015）构建了具有优先连接和增长的银行间市场无标度网络，并应用模拟的银行间数据来捕获网络中连接的大小和规模，使得整个网络更加契合实际银行网络。Jiang等（2008）基于无标度网络框架构建了金融产业集群的机构生成模型，该模型描述了在复杂社会行为下金融市场产业集群的生成机制。Lux（2015）研究了银行间市场简单动态模型中核心—边缘结构的形成。He等（2016）构建了企业银行代理人的内生信用网络模型，该模型描述了企业—企业、企业—银行和银行—银行之间内生的信贷关系。任小叶等（2014）基于表征异质投资群体结构的无标度网络的自组织金融模型，通过投资者在交易规则约束下的自组织聚簇行为，模拟金融市场的动态演化过程。

金融市场网络一般具有高聚类性，具有局域演化的特征。这是由于金融市场包括众多的细分子市场，且具有明显的区域特征，因此金融主体相关联的过程一般是围绕特定的资产市场或区域。为解决这一问题，Li和Chen（2003）提出了基于随机选取的局域世界演化网络模型。这一模型可以很好地应用于区域与地方金融的研究。

四、金融市场网络的风险传染

（一）金融市场网络结构对系统性风险传染的影响

金融市场网络可看作是金融系统各组成部分复杂关联关系的具体呈现，当金融风险在金融市场网络中迅速扩散并出现“多米诺骨牌效应”，系统性风險由此产生，因此系统性风险与金融网络结构特征是紧密相关的。本文通过对现有的文献进行梳理与总结，发现学界普遍认同金融网络结构是影响系统性风险传染的关键因素这一观点，但就金融网络结构是如何影响金融系统性风险传染的问题，目前尚没有统一的认识，有些观点甚至直接相悖（见表1）。例如，Allen等（2009）指出，完全连通结构网络更具稳定性，能更好抵御系统性金融风险，而Mistrilli（2011）的观点恰好与之相反，他认为在完全结构金融网络中，系统性风险传染概率更高。隋聪等（2016）认为网络集中程度越高，风险传染的可能性越小，而Lublóy（2005）认为网络集中程度与系统性风险不存在单调关系。经分析造成这些差异的主要原因在于网络结构的差异与系统性风险度量标准的不一致性，Allen等选取4家银行构建银行间网络，而Mistrilli却是以意大利银行间双边风险敞口数据构建的银行间网络，再加上Allen与Mistrilli采用了不同的系统性风险度量方法，所以造成了双方所得结论的巨大差异;同样的原因也造成了隋聪与Lublóy研究结论的差异。当前金融网络结构与系统性风险度量方法尚没有统一标准，因此构建更加贴近真实情况的金融市场网络，研究更加有效的系统性风险的度量方法，挖掘出不同金融情景下金融网络结构与系统性风险的内在联系依然是未来研究的重点。

（二）系统性金融风险传染模型

考虑金融风险传染机制，就不得不提到SIS与SIR这两种经典的传染病模型。自20世纪90年代以来，经济学家开始利用新兴传染病的流行病学来解释日益复杂的金融体系引发的冲击扩散现象，之后关于此方面的研究逐渐兴起。例如，Leitner等（2005）构建了动态银行网络风险传染救助模型，并将最优网络规模应用于银行系统间的联合责任安排和支付系统。Haldane等（2011）基于生态食物网的动态、传染病传播模型构建了金融系统风险传染模型，探讨了在简化金融网络模型中复杂性和稳定性之间的相互作用情况下，从这些模型中获取一些政策建议，以期减少系统性风险的发生。Arinaminpathy等（2012）提出了一种动态银行系统风险传染模型，该模型在传染病模型之上引入了用于捕捉系统中不稳定“信心”的机制，研究发现在对较大的银行施加比较小银行更为严格的资本要求情况下，可以有效减少系统中的不稳定“信心”，以此增加网络的弹性。Peckham（2014）建立全球金融危机传染模型，并指出在全球环境下追踪金融系统与生物系统中“传染”的概念对于理解风险的相互关联特征显得越来越重要。罗刚等（2015）基于SI模型提出担保网络的风险传播模型，并利用某金融机构的真实数据对模型进行了验证，研究发现网络的拓扑结构决定网络抵御系统性风险的能力。胡志浩等（2017）将传播动力模型SIRS引入无标度金融网络中，探讨了模型参数——感染率、治愈率、免疫失效率和网络紧密度对风险传染的影响。

五、研究述评与研究趋势

（一）研究述评

本文主要从研究方法与内容两个方面对当前金融市场网络结构与演化的研究进行评述。

在研究方法上：（1）目前关于金融市场网络的研究更多的还是基于Boss、Souma、Soramaki等人的实证统计视角，多是描述性、实证性的研究，然而利用数理模型来揭示金融市场网络结构演化与风险传染机制的研究还较少，并且关于这方面的研究多是系统动力学、物理统计背景的专家学者，金融领域的专家学者则较少，因此对金融市场网络结构演化与风险传染模型的研究还有较大的空间。（2）金融市场网络是一个多主体参与的动态网络，借助动态网络、加权网络、二分网络、多元复杂网络的方法更能准确地刻画金融市场网络的演化过程，但是目前综合这四个方面的金融市场网络的研究尚未出现。

在研究内容上：（1）目前关于金融市场网络的研究多聚焦于网络拓扑结构的实证统计上，关于金融市场网络动态演化过程的研究过少。研究金融市场网络的结构与演化机制是探索金融市场发展趋势的基础，需加强此方面的研究。（2）目前关于金融网络结构研究集中在小世界、无标度等几种典型的网络特征之上，更加细致的结构（例如社区、模体）分析的研究较少。无标度网络与小世界网络虽然在一定程度上可以刻画网络的演化过程，但实际金融市场网络节点的连接更加复杂，研究更加贴近金融市场网络演化过程的网络模型将是未来的研究重点。（3）由于金融网络结构的差异以及系统性金融风险度量方法的不一致性，使得学术界关于金融网络结构如何影响系统性风险传染的问题尚未达成共识，这给进一步研究留有较大空间。针对不同的金融情景，构建更加贴近真实情况的金融网络，研究更为适用的系统性风险度量方法，挖掘金融网络结构与系统性风险传染的内在关联依然是未来的研究重点。（4）目前关于金融市场网络传染模型的研究多基于SIS与SIR经典传染病模型及其改进模型，而该模型忽略了金融市场主体之间的差异以及主体之间的关联强度，简化了金融网络中复杂性和稳定性之间的相互作用，基于金融主体相对权重的网络传播模型更贴近真实的金融市场网络传播行为，然而目前此方面的研究还较少。

（二）研究趋势

上文提到的不足之处都是未来发展的重点，下面将从三个方向考察金融市场网络未来发展的趋势。（1） 金融市场网络结构生成机制研究。金融市场网络生成机制研究关注于金融市场动态演化过程中参与主体之间的相互作用。考察金融市场网络结构生成机制，是分析金融市场发展脉络的基础，是探索金融市场发展趋势的基础。通过研究金融网络生成机制可以有效地诠释网络内主体间的相互作用与网络外部表现之间的联系。（2）金融市场网络演化模型的研究。演化模型是金融市场网络内部作用与演化过程的数理表达，它是分析金融市场发展脉络的基础，也是探索金融市场发展趋势的基础。研究出能够刻画金融市场在时间维度上结构的演变，反映金融市场宏观资产市场与区域金融的变化演化模型将是未来的趋势。（3）金融市场网络中系统性风险传染机制研究。对系统性风险传染机制的研究可以有力地解释金融危机从“小冲击”到“大危机”的演变，并揭示了系统性风险微观成因与宏观成因之间的内在联系。从网络演化的视角研究金融风险的传染机制，虽能从全局的视角把控系统性风险的传染问题，但现有的研究过于简化金融市场主体以及他们之间的复杂性关系，以至于构建的传染模型不足以表征现实金融市场网络的复杂性，并且现有的传染模型主要聚焦于传染的机理与传染过程，较少关注风险源头，因此，聚焦于风险源构建更贴近真实金融市场网络的传染模型将是未来的研究重点。

參考文献：

[1]Bouchaud J P. 2008. Economics Needs a Scientific Revolution[J].Nature，455（7217）.

[2]Farmer J D，Foley D. 2009. The Economy Needs Agent-based Modelling.[J].Nature，460（7256）.

[3]Ruhl J B. 2016. Financial Complexity：Regulating Regulation[J].Science，352（6283）.

[4]Battiston S，Farmer D，F.ache A，et al. 2016. Financial Complexity：Accounting for Fraud--Response[J].Science，352（6283）.

[5]AngeliniI P，Maresca G，Russo D. 1996. Systemic Risk in the Netting System[J].Journal of Banking&Finance，20（5）.

[6]Boss M，Elsinger H，Summer M，et al. 2004. Network Topology of the Interbank Market[J].Quantitative finance，4（6）.

[7]Moussa A. 2011. Contagion and Systemic Risk in Financial Networks[D].New York：Columbia University.

[8]Cont R，Moussa A，Santos E B. 2013. Network Structure and Systemic Risk in Banking Systems[J].Social Science Electronic Publishing.

[9]Gai P，Haldane A，Kapadia S. 2011. Complexity，Concentration and Contagion[J].Journal of Monetary Economics，58（5）.

[10]Solorzano-Margain J P，Martinez-Jaramillo S，Lopez-Gallo F. 2013. Financial Contagion：Extending the Exposures Network of the Mexican Financial System [J].Computational Management Science，10（2-3）.

[11]Wan Y，Chen Z，Liu Z. 2006. Modeling the Two-power-law Degree Distribution of Banking Networks[J].Dynamics of Continuous Discrete and Impulsive Systems-Series B-Applications & Algorithms，13（3/4）.

[12]Aleksiejuk A，Holyst J A. 2001. A Simple Model of Bank Bankruptcies[J].Physica A Statistical Mechanics & Its Applications，299（1）.

[13]Allen F，Gale D. 2000. Financial Contagion[J].Journal of Political Economy，108（1）.

[14]Ladley D. 2013. Contagion and Risk-sharing on the Inter-bank Market[J].Journal of Economic Dynamics & Control，37（7）.

[15]Donaghy K P. 2000. Financial Networks：Statics and Dynamics[J].Journal of Regional Science，40（3）.

[16]Boccaletti S，Latora V，Moreno Y，et al. 2006. Complex Networks：Structure and Dynamics[J].Physics reports，424（4）.

[17]Watts D J，Ssrogatz S H. 1998. Collective Dynamics of“Small-world” Networks[J].Nature，393（6684）.

[18]Barabasi Si A L，Albert R. 1999. Emergence of Scaling in Random Networks[J].Science，286（5439）.

[19]Souma，Wataru，Fujiwara，et al. 2012. Complex Networks and Economics[J].Physica A Statistical Mechanics & Its Applications，324（1）.

[20]Soramaki K，Bech M L，Arnold J，et al. 2007. The Topology of Interbank Payment Flows[J].Physica A-statistical Mechanics & Its Applications，379（1）.

[21]Becher C，Millard S，Soramaki K. 2008. The Network Topology of CHAPS Sterling[J].Bank of England Quarterly Bulletin.

[22]Santos E B，Cont R. 2010. The Brazilian Interbank Network Structure and Systemic Risk[R].Central Bank of Brazil ：Tech Rep.

[23]Miranda R，Tabak B. 2013. Contagion Risk Within Firm-bank Bivariate Networks[R].Central Bank of Brazil： Research Department.

[24]De Masi G，Fujiwara Y，Gallegati M，et al. 2011. An Analysis of the Japanese Credit Network[J].Evolutionary&Institutional Economics Review，7（2）.

[25]De Masi G，Gallegati M. 2012. Bank-firms Topology in Italy[J].Empirical Economics，43（2）.

[26]Lee K E，Lee J W，Hong B H. 2007. Complex Networks in a Stock Market[J].Computer Physics Communications，177（1）.

[27]Li S，He J，Zhuang Y. 2010. A Network Model of the Interbank Market[J].Physica A Statistical Mechanics & Its Applications，389（24）.

[28]Thurner S，Hanel R，Pichler S. 2003. Risk Trading，Network Topology and Banking Regulation[J].Quantitative Finance，3（4）.

[29]Xu T，He J，Li S. 2016. Multi-channel Contagion in Dynamic Interbank Market Network[J].Advances in Complex Systems，19（06n07）.

[30]Jiang S S，Fan H，Xia M. 2018. Credit Risk Contagion Based on Asymmetric Information Association[J].Complexity，DOI： 10.1155/2018/2929157.

[31]Liu X F，Tse C K. 2012. A Complex Network Perspective of World Stock Markets：Synchronization and Volatility[J].International Journal of Bifurcation and Chaos，22（06）.

[32]Cao G，Shi Y，Li Q. 2017. Structure Characteristics of the International Stock Market Complex Network in the Perspective of Whole and Part[J].Discrete Dynamics in Nature and Society，3（1）：1-11.

[33]Vivier-Lirimont S. 2004. Interbanking Networks：Towards a Small Financial World？[R].Paris：Université Panth

éon-Sorbonne.

[34]Bech M L，Atclay E. 2010. The Topology of the Federal Funds Market[J].Physica A Statistical Mechanics & Its Applications，389（22）.

[35]Gao Y C，Wei Z W，Wang B H. 2013. Dynamic Evolution of Financial Network and Its Relation to Economic Crises[J].International Journal of Modern Physics C，24（02）.

[36]Chen Y W，Zhang L F，Huang J P. 2007. The Watts Strogatz Network Model Developed by Including Degree Distribution：Theory and Computer Simulation[J].Journal of Physics A Mathematical & Theoretical，4023（29）.

[37]Newman M E J，Watts D J. 1999. Renormalization Group Analysis of the Small-world Network Model[J].Physics Letters A，263（4-6）.

[38]Newman M E J. 2003. The Structure and Function of Complex Networks[J].Siam Review，45（2）.

[39]Philippas D，Koutelidakis Y，Leontitsis A. 2015. Insights into European Iinterbank Network Contagion[J].Social Science Electronic Publishing，41（8）.

[40]Jiang J，Li W，Cai X. 2008. Cluster Behavior of a Simple Model in Financial Markets[J].Physica A Statistical Mechanics&Its Applications，387（2）.

[41]Lux T. 2015. Emergence of a Core-periphery Structure in a Simple Dynamic Model of the Interbank Market[J].Journal of Economic Dynamics & Control，52.

[42]He J，Sui X，Li S. 2016. An Endogenous Model of the Credit Network[J].Physica A Statistical Mechanics & Its Applications，441（2）.

[43]Li X，Chen G. 2003. A Local-world Evolving Network Model[J].Physica A Statistical Mechanics & Its Applications，328（1）.

[44]Hasman A，Samartin M. 2008. Information Acquisition and Financial Contagion[J].Journal of Banking & Finance，32（10）.

[45]Alien F，Babus A. 2009. Networks in Finance[J].The Network Challenge：Strategy，Profit，and Risk in an Interlinked World，367（10）.

[46]Mistrulli P E. 2011. Assessing Financial Contagion in the Interbank Market：Maximum Entropy Versus Observed Interbank Lending Patterns[J].Journal of Banking&Finance，35（5）.

[47]Degryse H，Nguyen G. 2004. Interbank Exposure： An Empirical Examination of Systemic Risk in the Belgian Banking System[J].Social Science Electronic Publishing，4（2）.

[48]Gai P，Kapadia S. 2010. Contagion in Financial Networks[J].Proceedings of the Royal Society A：Mathematical，Physical and Engineering Sciences，466.

[49]Li S. 2011. Contagion Risk in an Evolving Network Model of Banking Systems[J].Advances in Complex Systems，14（05）.

[50]Nier E，Yang J，Yorulmazer T，et al. 2007. Network Models and Financial Stability[J].Journal of Economic Dynamics and Control，31（6）.

[51]May R M，Arinaminpathy N. 2009. Systemic Risk： the Dynamics of Model Banking Systems[J].Journal of the Royal Society Interface，7（46）.

[52]Acemoglu D，Ozdaglar A，Tahbaz-Salehi A. 2015. Systemic Risk and Stability in Financial Networks[J].American Economic Review，105（2）.

[53]Lublóy á. 2005. Domino Effect in the Hungarian Interbank Market[J].Hungarian Economic Review，52（4）.

[54]Lenzu S，Tedeschi G. 2012. Systemic Risk on Different Interbank Network Topologies[J].Physica A：Statistical Mechanics and its Applications，391（18）.

[55]Kermack W O，Mckendrick A G. 1927. A  Contribution to the Mathematical Theory of Epidemics[J].Proceedings of the Royal Society of London.Series A，Containing papers of a Mathematical and Physical Character，115（772）.

[56]Kermack W O，Mckendrick A G. 1932. Contributions to the Mathematical Theory of Epidemics.II.—The Problem of Endemicity[J].Proceedings of the Royal Society of London.Series A，Containing Papers of a Mathematical and Physical Character，138（834）.

[57]Leitner Y. 2005. Financial Networks：Contagion，Commitment，and Private Sector Bailouts[J].The Journal of Finance，60（6）.

[58]Haldane A G，May R M. 2011. Systemic Risk in Banking Ecosystems.[J].Nature，469（7330）.

[59]Arinaminpathy N，Kapadia S，May R M. 2012. Size and Complexity in Model Financial Systems[J].Proc Natl Acad Sci U S A，109（45）.

[60]Peckham R. 2014. Contagion：Epidemiological Models and Financial Crises[J].Journal of Public Health，36（1）.

[61]林福永，孙凯.复杂网络关系流与行为关系定理——一般系统结构理论在复杂网络中的应用[J].系统工程理论与实践，2007，27（9）.

[62]张卫国.金融复杂系统的演化与控制研究[M].北京：科学出版社，2017.

[63]陈少炜，李旸.我国银行体系的网络结构特征——基于复杂网络的实证分析[J].经济问题，2016，53（8）.

[64]范宏.动态银行网络系统中系统性风险定量计算方法研究[J].物理学报，2014，63（3）.

[65]贾彦东.金融机构的系统重要性分析——金融网络中的系统风险衡量与成本分担[J].金融研究，2011，（10）.

[66]陈建新，罗伟其，庞素琳.银行风险传染的集合种群模型——基于元胞自动机的动态模拟[J].系统工程理论与实践，2012，（3）.

[67]张来军，杨治辉，路飞飞.基于复杂网络理论的股票指标关联性实证分析[J].中国管理科学，2014，22（12）.

[68]万阳松，陈忠，陈晓荣.复杂银行网络的宏观结构模型及其分析[J].上海交通大学学报，2007，41（7）.

[69]刘海飞，柏巍，李冬昕，等.沪港通交易制度能提升中国股票市场稳定性吗？——基于复杂网络的视角[J].管理科学学报，2018，21（1）.

[70]庄新田，闵志锋，陈师阳.上海证券市场的复杂网络特性分析[J].东北大学学报（自然科学版），2007，28（7）.

[71]秦春雷，张巍，朱艳春.金融危机下证券市场网络结构演化的实证分析[J].商业研究，2015，57（3）.

[72]王莹.全球外汇市场网络结构、货币影响力与货币社区[J].世界经济研究，2018，288（2）.

[73]黄玮强，庄新田，姚爽.中国股票关联网络拓扑性质与聚类结构分析[J].管理科学，2008，21（3）.

[74]李进，马军海.交叉持股行为的复杂性研究[J].北京理工大学学报（社会科学版），2009，11（4）.

[75]张骥，龙海明.基于系统性风险背景的证券市场网络动态演化[J].求索，2017，14（4）.

[76]韩冬梅，王雯.复杂网络视角下的国际证券市场结构特征分析[J].复杂系统与复杂性科学，2014，11（3）.

[77]李旲，曹宏铎，邢浩克.基于复杂网络少数者博弈模型的金融市场仿真研究[J].系统工程理论与实践，2012，32（9）.

[78]任小叶，周佩玲.基于无标度网络的自组织金融模型研究[J].中国科学技术大学学报，2014，44（1）.

[79]陈庭强，何建敏.基于复杂网络的信用风险传染模型研究[J].中国管理科学，2014，22（11）.

[80]范小云，王道平，刘澜飚.规模，关联性与中国系统重要性银行的衡量[J].金融研究，2012，38（11）.

[81]隋聪，谭照林，王宗尧.基于网络视角的银行业系统性风险度量方法[J].中国管理科学，2016，24（5）.

[82]黄聪，贾彦东.金融网络视角下的宏观审慎管理——基于银行间支付结算数据的实证分析[J].金融研究，2010，22（4）.

[83]胡宗义，黄岩渠，喻采平.网络相关性，结构与系统性金融风险的关系研究[J].中国软科学，2018，8（1）.

[84]罗刚，赵亚伟，王泳.基于复杂网络理论的担保网络风险传播模式[J].中国科学院大学学报，2015，32（6）.

[85]胡志浩，李晓花.复杂金融网络中的风险传染与救助策略——基于中国金融无标度网络上的SIRS模型[J].財贸经济，2017，38（4）.