极靴式永磁同步电机径向气隙磁密分析

张明哲，杜钦君，王爱传，高志东，王 平，刘 坤

(1.山东理工大学 电气与电子工程学院，山东 淄博 255000；2.山东五征集团有限公司，山东 日照 276800；3.潍坊市电机一厂有限公司，山东 潍坊 261000；4.淄博职业学院，山东 淄博 255000)

0 引 言

表贴式永磁同步电机具有功率密度高、效率高的优点，在航天、汽车、机床等行业有广泛的应用前景[1]。普通表贴式矩形永磁钢永磁同步电机的空载径向气隙磁密并不是标准的正弦波形，含有大量的谐波，将永磁钢加工成复杂形状改善径向磁密波形的方式会增加电机生产成本[2]，因此，使用一种低成本的方式优化径向气隙磁密具有重要意义。

文献[3]利用谐波建模法建立了考虑导磁材料磁导率的气隙磁场解析模型。文献[4-5]将电机分为永磁钢、气隙、电枢槽等求解子域，分析了考虑齿槽影响的空载磁场和电枢反应磁场。文献[6]把永磁钢看为电流等效面，结合子域模型法，建立了空载磁场解析模型。上述文献表明能够利用解析法准确计算气隙磁密，但没有提供磁极高度连续变化时计算径向气隙磁密的方法。文献[7-8]研究了Halbach充磁方式下电机气隙磁场分布，并对电机结构进行了优化，文献[9]研究了组合高度不等的表贴式永磁钢Halbach充磁方式下对于电机性能的影响。文献[7-9]表明了加工复杂形状的永磁钢和改变永磁钢充磁方向的方法能够提高径向磁密波形正弦度，但是也增加了电机加工成本。

本文提出一种在矩形永磁钢表面加装极靴的外转子永磁同步电机磁极结构，利用标量磁位法和相对比磁导函数建立考虑齿槽效应影响的空载径向气隙磁密解析模型，使用有限元软件研究极靴结构参数对电机径向气隙磁密的影响规律，获得最优结构参数。

1 径向气隙磁密建模及有限元验证

1.1 径向气隙磁密建模

加装极靴的外转子永磁同步电机结构如图1，该结构采用低成本矩形永磁钢，永磁钢平行充磁，极靴与永磁钢等宽，两端有一定的厚度，极靴表面为圆弧形。在极靴、永磁钢和转子铁心上开设螺钉孔，使用沉头螺钉将极靴和永磁钢固定在转子铁心上。加装圆弧形极靴后可实现不均匀气隙，有效提高径向磁密波形正弦化程度。

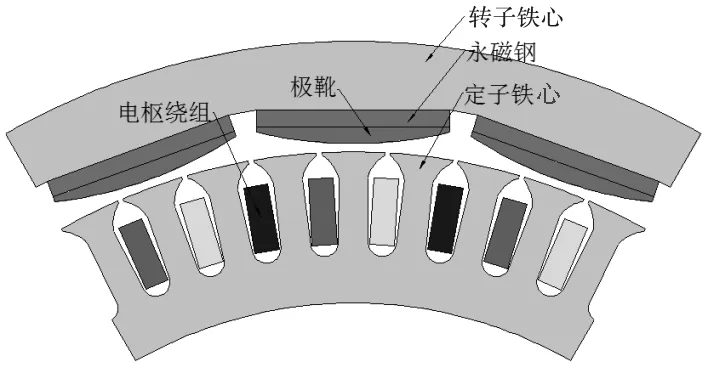
图1 极靴式磁极永磁同步电机

切向气隙磁密较小，一般可忽略不计，因此，本文以加装极靴的外转子永磁电机进行径向气隙磁密的模型推导和计算，该模型同样适用于具有非均匀气隙结构的内转子电机。在建立解析模型时，为了简化计算，做以下假设：

(1)定子齿表面光滑；

(2)槽深为无限深；

(3)铁心和极靴磁导率为无穷大；

(4)永磁钢表面剩磁分布均匀。

空载时，求解区域内无电流，可用标量磁位φ作为位函数，将求解区域分为气隙域和极靴域，在不同的求解域中，磁感应强度B与磁场强度H之间的关系为：

(1)

式中，M为极靴的磁化强度；μ0为真空磁导率，μ0=4π×10-7H/m；μr为永磁钢的相对磁导率，由永磁钢的材料和加工方式决定。

M=Mrr+Mθθ

(2)

式中，Mr为M的径向分量，Mθ为M的切向分量。

忽略永磁钢与极靴之间的缝隙，极靴中线处与定子齿的距离最小，根据磁路最小原则，极靴中部的磁通大部分受定子齿影响形成径向分布，产生聚磁效应，磁通密度约为永磁钢剩磁的1.1倍，极靴两端视为与永磁钢充磁方向相同的平行分布，磁通密度约为永磁钢剩磁的0.9倍。极靴磁化强度切向分量较小，可以忽略不计。极靴的磁化强度径向分量Mr为

(3)

式中，p为电机极对数；Bm为永磁钢表面剩磁；θ为机械角度；αp为极弧系数；β为极靴磁通径向分布的长度占极靴总长的比例。

将磁化强度径向分量用傅里叶级数展开得：

(4)

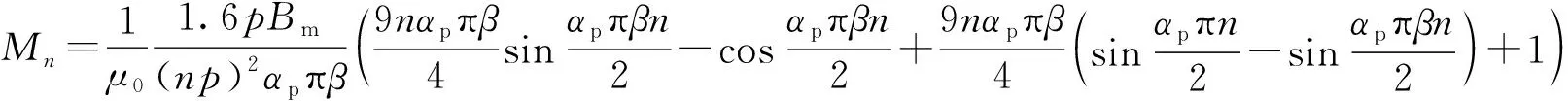
(5)

对于标量磁位有：

(6)

φ在空气域满足拉普拉斯方程，在极靴域满足泊松方程。

(7)

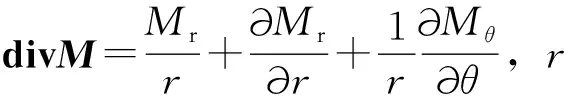
将式(7)展开即为

(8)

该方程的通解为

(9)

(10)

式中，An1、Bn1、An2、Bn2为待定系数。

磁场强度与标量磁位的关系为

(11)

由式(11)得到定解条件为

(12)

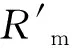
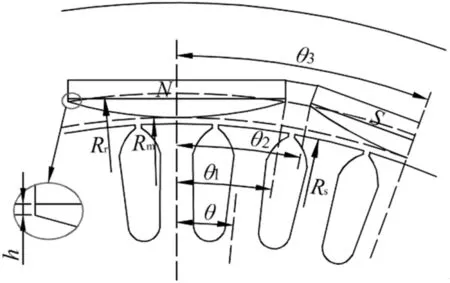
图2 电机尺寸示意图

(13)

式中，θ1=αpπ/2p；θ2=π/p-αpπ/2p；θ3=π/p。

将定解条件代入通解方程中，得到待定系数为

(14)

(15)

(16)

(17)

式中，Cn、Dn、En、Fn为

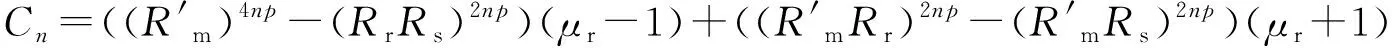
(18)

(19)

(20)

(21)

求解得到气隙磁密径向分量为：

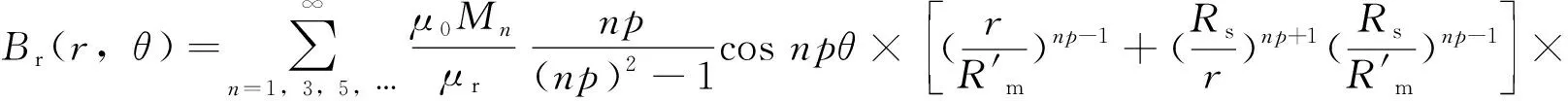
(22)

根据式(22)即可计算得到定子无槽时的径向气隙磁密分布，但在永磁电机中定子都会开槽，由于空气和定子齿的磁导率相差较大，定子开槽会使气隙磁导不均匀，导致气隙磁密中含有较大幅值的谐波，本文构造了非均匀气隙相对比磁导函数，能够准确计算齿槽效应对于径向气隙磁密的影响。

对定子槽口引起的磁密波形变化可利用余弦函数进行拟合，由卡特系数的定义得：

(23)

式中，S1为一个槽对气隙磁密的影响宽度。

(24)

式中，b0为槽口的宽度；

(25)

式中，hm为永磁钢的充磁方向长度；g(θ)为气隙长度，求得g(θ)为

(26)

在任意气隙半径r处，由许-克变换得：

(27)

其中v由下式决定

(28)

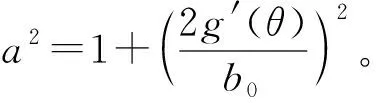
定子齿表面和定子槽口的相对比磁导函数分别为

(29)

式中，ts为定子齿宽；Qs为定子槽数。

联立式(22)与式(29)即可计算出定子开槽时气隙内半径r处的径向气隙磁密分布：

(30)

1.2 有限元验证

以3相18极54槽外转子永磁同步电机为例，永磁钢材料为钕铁硼N35，极靴材料为电工软铁。电机主要结构参数如表1。

表1 电机主要结构参数

将表1中的参数代入式(30)，得到径向气隙磁密解析计算结果有与限元计算结果对比如图3，解析计算结果与有限元计算结果吻合良好，利用相对比磁导函数计算的定子开槽引起的磁密波形凹陷与有限元计算结果基本相符，验证了解析模型的正确性。

图3 有限元结果与解析结果对比

2 极靴参数对气隙磁密的影响规律

由式(22)知，电机结构确定后，影响径向气隙磁密分布的极靴参数即为极靴两端厚度h和极弧系数αp，本文利用有限元软件分别计算h和αp对于径向气隙磁密的影响规律。取极靴中间厚度为3 mm，h的变化范围为0～3.0 mm，步长为0.50 mm，取极弧系数变化范围为0.70～0.95，步长为0.50 mm。

使用波形畸变率(THD)量化波形的正弦化程度，THD越小，谐波成分越少，波形正弦化程度越高，THD的计算公式如下：

(31)

式中，Gk为k次谐波幅值；G1为基波幅值。

计算得到不同极靴参数下的径向气隙磁密THD如图4。在h=0～2.0 mm时，随着αp的增加，THD逐渐减小，在h=2.5～3.0 mm时，随着αp的增加，THD逐渐增加。在h=0～2.5 mm时，αp不变、随着h的增加，THD逐渐减小，在h=3 mm时，极靴形状为矩形，气隙磁密波形正弦性差，THD较大。

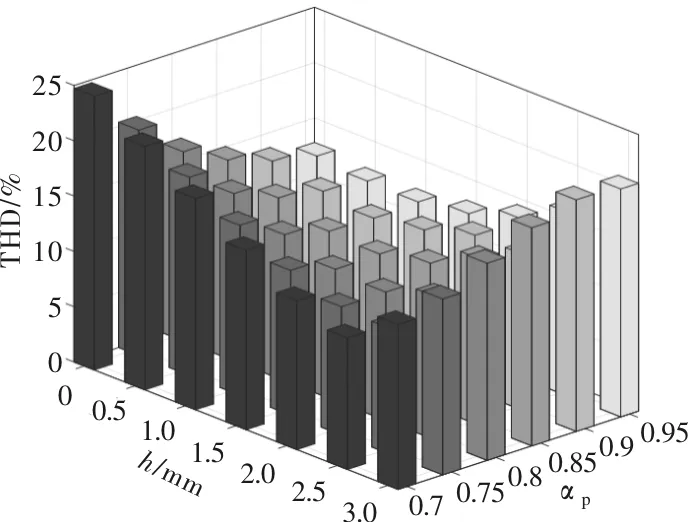
图4 径向气隙磁密THD

计算得不同极靴参数下的径向气隙磁密幅值如图5。随着h和αp的增加，径向气隙磁密幅值逐渐减小，这是由于h和αp变大增加了漏磁通。

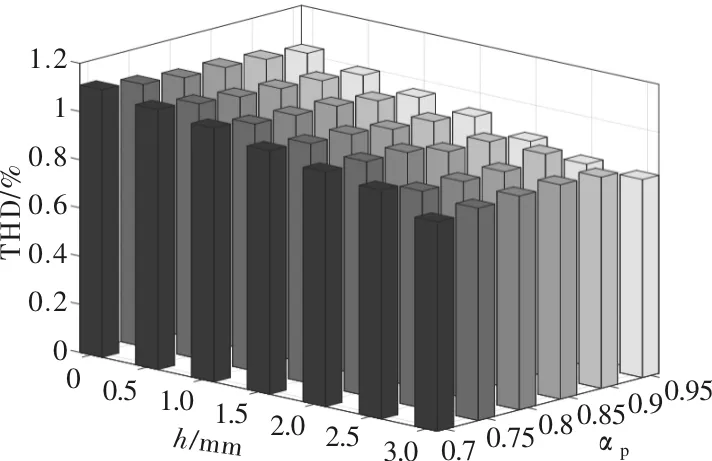
图5 径向气隙磁密幅值

综合比较不同极靴参数下的径向气隙磁密THD和幅值，选取h=1 mm和αp=0.85为极靴的最优参数，计算得到加装极靴的径向气隙磁密和未加装极靴的径向气隙磁密，对比曲线如图6。未加装极靴的径向气隙磁密THD为24.77%，幅值为0.91 T，加装极靴后径向气隙磁密THD为12.21%，幅值为1.01 T，加装极靴后径向气隙磁密THD减少，幅值提高。

图6 径向气隙磁密对比

3 结 语

本文建立了极靴式永磁同步电机的空载径向气隙磁密解析模型，通过有限元仿真验证了解析模型的正确性，此模型可应用于连续变化的非均匀气隙结构，为设计非均匀气隙永磁同步电机提供了理论参考。基于解析模型分析了极靴两端厚度和极弧系数对于径向气隙磁密的影响规律，获得了最优结构参数。