5-DOF混联雕刻机速度运动学分析及仿真
张道义,伞红军,陈久朋,李鹏飞,熊彬州
(昆明理工大学 机电工程学院,云南 昆明 650500)
并联机器人由于其高刚度、输入误差不积累、承载能力强等特点,已成为机器人领域的研究热点之一[1-5]。而少自由度并联机构由于其结构简单、成本低廉等优点具有广阔的应用前景[6]。随着科学技术的发展,简单的并联机构难以满足工业生产的需要,而串并联机构则因兼具并联机构和串联机构的优点而有着更广泛的应用前景。一般来说,串并联机构是由三自由度以下的并联机构与三自由度以下的串联机构连接而成[7]。90年代以来,国内外对串并联机构进行了广泛的研究。国内哈尔滨工业大学和燕山大学开展了串并联机构的研究工作:黄田等人在Tricept robot基础上设计的空间非对称TriVariant机构[8-10]。傅江勋研究了具有3条腿的六自由度并联机器人,并计算出了机器人的正运动学和逆运动学。结果表明,该方法提高了机器人的精度,验证了运动学分析的有效性[11]。康件丽利用MATLAB软件分析了3-PRS并联机器人的速度和加速度[12]。武雅杰等对机器人的路径进行了规划[13]。雷俊松用多项式研究了混合机器人的轨迹规划,给出了3个滑块的位移、速度和加速度曲线[14]。朱呈祥等人基于MATLAB和ADAMS对超速机柔性轴系进行了仿真分析,得出了瞬态和稳态情况下的运行情况[15]。
采用矢量法和导数法对五自由度混联雕刻机的速度进行了分析,对五自由度雕刻机的实际编程作业提供了便利。
1 机器人的结构特点
五自由度混联雕刻机由并联部分和串联部分组成,其中并联部分主要由步进电机、定平台、动平台、3个空间呈现120°夹角的平行四边形机构和3个互成120°竖直分布的滚珠丝杠构成。步进电机控制滚珠丝杠的螺杆运动,其通过螺母滑块将旋转运动变成竖直方向的移动,每条支链的复合运动即为动平台中心点的运动。并联机构的动平台上串联一个二自由度的机构,一个绕串联部分坐标系z轴旋转,一个绕y轴旋转。雕刻机的三维模型如图1所示。
2 机构位置分析
位置分析是机构运动学分析的核心内容之一,是机构速度分析、加速度分析、工作空间分析及力学分析等的基础。由于平行四边形机构的4个转动副轴线始终同另两个转动副轴线垂直正交,所以平行四边形机构可取对边中点的连线进行简化以便于对机器人进行分析。图2为混联雕刻机的机构简图,其虚线部分为简化的平行四边形机构。
在图2中,Ai(i=1,2,3)为3立柱与静平台的交点,Bi(i=1,2,3)为平行四边形机构虚拟连杆与移动副滑块相接的转动副的形心,Ci(i=1,2,3)为虚拟连杆与动平台相接的转动副的形心,A1A2A3构成了圆心为O且外接圆半径为R的等边三角形。同理C1C2C3构成了圆心为G且外接圆半径为r的等边三角形。在动平台和静平台的圆心分别建立动坐标G-xGyGzG和静坐标系O-xOyOzO,在雕刻机末端刀具参考点P建立坐标系P-xPyPzP。其中zG和zO分别垂直于动、静平台,并且方向沿平面向上;xG和xO分别指向点A1和C1;xP正向与机器人末端刀具轴向方向相同。
3 拓扑学分析机构自由度
机构拓扑结构学为运动学与动力学提供了新的统一建模方法,来构建现代机构学的新理论体系[16]。图3是机构的支链简图。
图3中的4R机构(即4个Ra转动副组成的平行四边形机构)可以用一个移动副来代替,从而对支链进行简化。图4所示为雕刻机并联部分的简化结构。
在并联部分,3条支路的拓扑机构为
SOC{-Ri1-Pi2-Ri3⊥Pi4},i=1,2,3
其中,Ri1‖Ri3。
选定动平台上任意一点为基点O。确定支路末端构件的方位特征集
同理可得到另外两条支链的方位特征集
确定第一回路的独立位移方程数:因为R11不平行R21,故以第一、二条支链作为第一个独立回路,第一个独立回路的独立位移方程数ξL1为
故第一、二条支路所组成的子并联机构的自由度为
其中,m为运动副数;fi为第i个运动副的自由度。考虑到R11不平行R21且F(1-2)=3,可知第一、二条串联支链组成的并联机构的方位特征集为
确定第二回路独立位移方程数:第二个独立回路的独立位移方程数ξL2为
确定机构的自由度:并联机构的自由度为
在并联机构的动平台上串联了两个轴线不平行的转动副,故为机构增添了两个转动自由度,因此混联雕刻机的自由度为
F=Fa+2=5
(1)
即此混联雕刻机具有三维移动和绕两个转动副轴线旋转二维转动。
4 矢量法分析雕刻机速度正运动学
4.1 雕刻机并联部分速度分析
图5为机构的速度映射关系简图,V为机构动平台中心点G的速度;ω为动平台的转动角速度;Ri为铰点Ji(动平台3个铰点,(i=1,2,3))到参考点G的矢径;Vji为铰点Ji的速度;ni为平行四边形机构杆长Li的单位方向矢量;vi为3个滑块上下运动的速率。
由上文运用机构拓扑理论计算雕刻机的自由度分析可知,该雕刻机并联部分的动平台在笛卡尔坐标系中只具有沿着x、y和z3个方向的平移运动,动平台的变化仅仅是针对定平台的位置变化,不存在姿态的变化,故动平台不存在角速度和角加速度。
根据机构驱动杆的驱动速度与动平台的运动速度之间的映射关系,则有
VJi=V,i=1,2,3
(2)
vi=VJi·ni·cosαi,i=1,2,3
(3)
其中,αi为立柱与平行四边形之间的杆的夹角。将式(2)代入式(3)得到
(4)
把式(4)展开,对于全部3个滑块,有
(5)
式(5)可写成矩阵形式
(6)

(7)
式(7)可以改写成为
(8)
4.2 雕刻机的末端速度分析

根据此混联雕刻机的结构特点,其速度分析应分两步来完成:
(1)已知3个滑块的输入速度(v1,v2,v3)求解雕刻机动平台参考点(动坐标系的原点G)的输出速度V(Vx,Vy,Vz)。

图6为混联雕刻机的速度分析简图。
根据图示的速度传递关系和速度合成定理,有如下关系式成立
Vn=V
(9)
(10)
(11)
(12)

将式(11)代入式(12)得到
(13)
将式(10)代入式(13)可以得到
(14)
(15)
式(12)可以表示为矩阵形式
(16)
将式(15)~式(16)合并成如下的矩阵相乘形式
(17)
若令矩阵
(18)
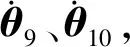
4.3 雕刻机加速度分析
混联雕刻机的加速度分析,分为并联部分的加速度分析和雕刻机加速度分析两部分。
(1)并联部分的加速度分析。 将式(3)两端分别求导可得
(19)
式中,αi为第i个滑块输入的加速度;AJi为铰点Ji的加速度。式(19)可写成矩阵形式
(20)
根据加速度合成定理可知
AJi=A
写成矩阵形式得
[AJi]=[A]
(21)
式中,A为动平台参考点,也就是动平台原点的加速度。式(2)可以写成如下矩阵形式
[VJi]=[V]
(22)
式(3)可以写成如下矩阵形式
(23)
将式(22)代入式(23)可得
(24)
将式(21)、式(22)及式(24)代入式(20)整理得
(25)
式中,[Ui]为加速度传递矩阵分量
(26)
(27)

(28)
(2)雕刻机加速度分析。令εm=[εmxεmyεmz]T表示刀具输出的角加速度,Am=[AmxAmyAmz]T表示刀头点m的输出加速度,εn=[εnxεnyεnz]T表示动平台上n点的角加速度,An=[AnxAnyAnz]T表示动平台上n点的加速度。通过加速度合成定理可以得出
(29)
(30)
(31)
(32)
5 求导法分析雕刻机速度逆运动学
前文介绍了当滑块速度和加速度均为已知时,采用矢量法求解雕刻机速度和加速度的过程。下面将根据已知的雕刻机的速度和加速度,并采用求导法结合MATLAB来求解3个滑块的速度。求解滑块速度时分两步完成:(1)已知刀头点速度和加速度求动平台的速度和加速度;(2)已知动平台速度和加速度求解3个滑块速度和加速度,以下为具体计算过程。
设末端刀头点位置坐标m=[pxpypz]T,该刀头点的姿态主要由垂直于动平台的电机转角θ9和摆角θ10决定。设G=[uvw]点为动平台的位移。则动平台中心点的位移矢量可以表示为
(33)
由前面拓扑理论算并联部分的自由度可知,并联部分只有沿x、y、z3个方向的自由度,也就是动平台相对于定平台只有位置的变化没有姿态的变化。故动平台到定平台的齐次变换矩阵为
(34)

滑块R1、R2、R3的高度为
(35)
式中,mi为滑块的高度;Li为连杆长度;xBi为Bi的x轴坐标,yBi为Bi的y坐标。由上述的式(33)可以看出滑块的高度是动平台中心点位移的函数,而u、v、w又是时间t的函数,因此上式可表示为
mi(t)=Fi(u(t),v(t),w(t))
(36)
上式两边对时间t求导,得
(37)
则3个滑块速度与末端速度的关系为
(38)
式中,矩阵J为
(39)
上式两边对时间t求导,得加速度之间的关系为
(40)
由上述分析可知:已知动平台中心点的位置矢量,可以通过对时间求导来获得3个滑块的速度和加速度。而动平台中心点的位置矢量取决于末端刀头点的位置参数(刀头点的位置矢量m=(pxpypz)T和两个电机转角θ9和θ10)。
6 速度和加速度分析
6.1 速度算法验证

雕刻机的速度和角速度曲线如图7和图8所示。
为了验证雕刻机速度算法的正确性,首先在ADAMS中选择模型的每个驱动副并修改驱动函数。在函数列中,将速度和角速度的驱动函数分别添加到3个棱柱副和两个转动副中,设定仿真时间为20 s,仿真步长为500。通过仿真可以得到端点M的输出速度曲线(图9)和角速度曲线(图10)。
通过对比分析可知:图7、图8中端点的速度和角速度曲线与图9、图10中端点的速度和角速度曲线完全相同,证明了雕刻机速度算法的正确性。
6.2 加速度算法验证

根据前面推导的加速度算法,图11和图12为通过MATLAB计算出的雕刻机末端加速度曲线和角加速度曲线。
为了验证雕刻机速度算法的正确性,在ADAMS环境下修改每个驱动的驱动函数。在函数列中,将加速度和角加速度的驱动函数分别加到3个棱形副和两个转动副中。设定仿真时间为20 s,仿真步长为500。通过仿真可以得到端点M的输出加速度曲线(图13)和角加速度曲线(图14)。
通过分析得知图11、图12中端点的加速度和角加速度曲线与图13、图14中端点的加速度和角加速度曲线完全相同,从而验证了雕刻机加速度算法的正确性。
7 结束语
本文在三自由度并联机构的基础上串联二自由度的串联机构构成了五自由度的混联雕刻机,该雕刻机能够实现复杂曲面的加工,对工业生产能够起到一定的积极作用。文章首先运用机构拓扑理论求解雕刻机的自由度。运用矢量法对刀头末端的速度和加速度进行了正向运动学分析,然后采用求导法对滑块的速度和加速度进行了逆向分析,最终通过MATLAB验证计算及算法的正确性,为后续对混联雕刻机的控制提供了便利。

