某大跨度钢箱提篮拱桥弹塑性承载力分析
李帅斌
(华南理工大学土木与交通学院 广东 广州 510640)
一、引言
在一些气候环境恶劣的地区或在优良地质下建造铁路桥梁,钢拱桥是优先选择。拱桥是一种以承压为主的压弯体系,随着拱桥跨度的增大拱肋长细比越来越大,这更加凸显了拱桥的稳定性问题。
按照失稳形式,拱桥的稳定问题可分为第一类稳定(又称为分支点失稳)和第二类稳定(又称为极值点失稳)。目前普遍采用线弹性理论进行拱桥稳定分析,但只考虑线弹性计算的稳定系数远远大于实际拱桥承载力,与实际结构不符[1]。应充分考虑结构部分区域已经产生屈曲的现象,满足实际受力情况。
拱肋在制造、运输过程中会出现拱肋的初始弯曲、装配误差等初始缺陷,拱轴线往往偏离设计,应考虑其影响。
二、工程概况
所依托桥梁为肇庆市一大跨径高速铁路拱桥,大桥全长618.3m,桥跨布置:(41.2+486+49.1)+1-32m预应力混凝土简支梁,主桥为中承式钢箱提篮拱桥,计算跨径450m,桥型布置如图1所示。
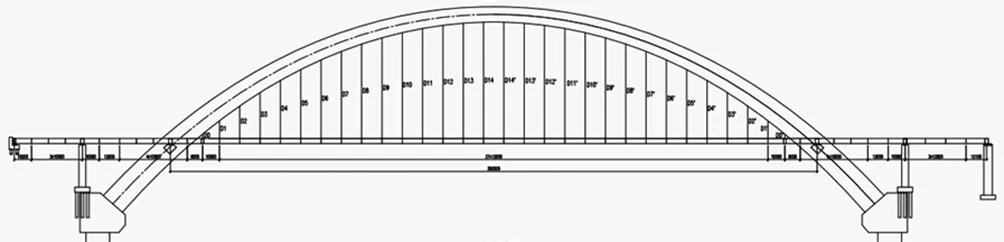
图1 桥型布置图
三、桥梁有限元模型
(一)拱桥非线性分析
拱桥的非线性主要包括几何非线性以及材料非线性。材料非线性体现在进行加卸载的过程是不可逆的,桥梁几何非线性为大位移,小应变问题。本文在进行拱桥弹塑性承载力分析时考虑几何、材料非线性、初始缺陷三个因素。采用计入材料非线性的U.L列法,其有限元方程为:
(t[KEP]+t[KG]){Δδ}={ΔP}
(1)
其中,t[KEP]为结构的弹塑性刚度矩阵,t[KG]应力刚度矩阵,Δδ为位移增量,ΔP为荷载增量。对结构而言,其最危险的几何缺陷类型与弹性临界屈曲模态形状一致,提取特征值分析一阶模态位移结果,按一定比例施加给原结构形成新的各节点坐标[7]。本文取该比例因子α为0.075,各节点坐标增量如下:
Δ=δ·α
(2)
其中,δ为各节点最大位移,Δ为各节点坐标增量。
(二)截面特性
利用ABAQUS进行全桥建模。拱肋为两箱截面,横撑、桥面系纵横梁为单箱截面,B31单元进行建模;吊杆采用杆单元,降温法施加吊杆力;对拱脚处,主梁两端固接,辅助墩处、拱肋及主纵梁相交处约束其横向及竖向位移。全桥划分为2246个单元,1802个节点。
考虑桥梁恒载(结构自重和桥面铺装、吊杆力)及活载(列车荷载及风荷载),设5种荷载工况:(1)恒载+全跨列车活载;(2)恒载+单幅列车活载;(3)恒载+半跨列车活载;(4)恒载+风载;(5)恒载+全跨列车活载+风载。
(三)线弹性稳定分析
针对以上5种工况,对全桥进行线弹性特征值屈曲分析,其一阶稳定系数如表1所示:

表1 一阶稳定系数
在理想情况下随着承载以及受荷范围的增大,全桥的线弹性稳定系数会逐渐降低。在列车运行的过程中,列车刚进入主桥、只有单侧列车通行、双侧均有列车通行三种情况,其稳定系数依次减小。
(四)非线性稳定分析
对全桥进行5种工况的非线性分析,得到拱顶竖向、1/4跨竖向荷载-位移曲线,如图2所示。仅受面内荷载时,全跨单幅受载比单跨双幅受载更为安全。与线弹性分析结果对比,列车刚进入主桥时稳定系数最小,这也说明全桥所受荷载的非对称程度越高其稳定性越差。
从荷载-位移曲线可以看到,本桥没有因结构达到临界状态而失去稳定性,在极值点之后维持了一定的承载能力。5种工况,弹塑性稳定分析结果均小于线弹性稳定分析结果,证明仅采用线弹性理论不能满足桥梁设计;全桥受载的非对称性比强度对稳定性的影响更大。
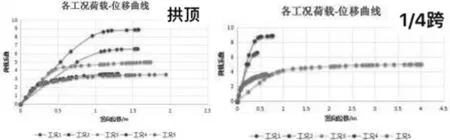
图2 拱顶及1/4跨竖向荷载-位移曲线
四、结论
(1)对本文分析的拱桥模型,线弹性稳定分析的稳定系数最大约为23,而非线性稳定分析仅为4左右,线弹性分析远不能满足结构设计的需要。
(2)考虑拱肋非线性,与其他工况相比,风荷载工况稳定性最差,一方面是因为结构的面外刚度不如结构的面内刚度,另一方面是因为横向荷载会导致结构产生较大的变形。
(3)由以上对本桥的分析可看到,不同荷载工况下,全桥安全稳定系数有较大差异,因此,应充分考虑不同荷载工况对全桥的整体稳定性的影响;此外,当全桥所受荷载达到临界状态时不会立刻失去承载力,具有较好的延性。

