装配整体式网格剪力墙压弯承载力计算方法

李 斌，黄 炜

(1.西安工程大学城市规划与市政工程学院，西安 710600；2.西安建筑科技大学土木工程学院，西安 710055)

历次震害和试验表明：装配式混凝土结构的倒塌和预制构件的破坏中，主要原因在于构件之间的连接失效，因此，必须采取可靠的连接技术，才能有效保证装配式结构的整体性[1－6]。装配整体式网格剪力墙结构主要由预制混凝土墙板、现浇边缘连接构件(包括竖向边缘构件、连接柱及暗梁)及现浇或叠合楼板装配整浇而成。其中，预制混凝土墙板与现浇竖向边缘连接构件组成的墙肢或墙段作为结构的主要受力构件。墙板内采用延性布筋方式—井字型布筋，并在端部设置可靠竖向及水平连接以保证该结构的抗震性能及耐损伤能力。文献[7]对底部预留后浇区钢筋搭接的装配整体式剪力墙进行抗震试验分析，认为在底部预留混凝土后浇区采用搭接连接的剪力墙体的承载力与现浇结构基本一致。文献[8]提出一种配有X型斜筋的新型水平后浇接缝的连接方法，并进行试验研究。结果表明：当装配整体式剪力墙水平接缝采用合理的连接方法，可实现与现浇结构等同的抗震性能。文献[9]对一栋 3层足尺的新型装配整体式混凝土剪力墙子结构进行拟静力试验，试验结果未出现承载力失效，认为该结构体系的抗震性能等同于现浇剪力墙结构。文献[10]研究了装配整体式双向孔空心模板剪力墙的受剪承载力，提出当轴压比和水平钢筋配筋率提高时，墙体的受剪承载力和变形能力均有所提升。文献[11]对钢筋浆锚连接装配式剪力墙的破坏机理进行分析，并提出改进型钢筋浆锚连接装配式剪力墙接缝的压弯承载力计算方法，所提出的计算公式可用于该结构的承载力设计。

本文以提高装配整体式网格剪力墙压弯性能为目的，进行低周反复加载试验[12－13]；重点研究预制墙板竖向钢筋连接方式、竖向接缝形式、墙板布筋方式等关键因素对该墙体压弯性能的影响。对试验结果进行研究，并基于平截面假定，充分考虑预制墙板可靠连接钢筋作用，忽略未连接钢筋作用，建立墙体在开裂、屈服、峰值、极限状态弯矩-曲率计算方法，并对影响装配整体式网格剪力墙压弯承载力参数进行分析。

1 试验简介及结果分析

1.1 试验概况

本次试验共制作6榀墙体，分别考虑预制墙板竖向钢筋连接方式、预制墙板竖向接缝形式、预制墙板配筋形式对墙体抗震性能的影响。试件编号依次为MPGSW-1~MPGSW-6。设计轴压比均为0.2。具体设计参数变化见表1；所有试件的尺寸均相同，墙体截面尺寸为hw×bw=1400 mm×100 mm，墙高Hw=1450 mm。试件具体配筋见图1；预制墙板与现浇边缘构件均采用普通混凝土浇筑，强度等级按C30设计。实测普通混凝土立方体抗压强度平均值为 34.86 MPa。预制墙板底部预埋焊板尺寸为120 mm×100 mm×10 mm；底梁预埋焊板尺寸为200 mm×150 mm×10 mm，具体构造详图见图1(h)。6榀试件施工情况见文献[12]。

表1 试件设计参数Table 1 Design parameters of specimens

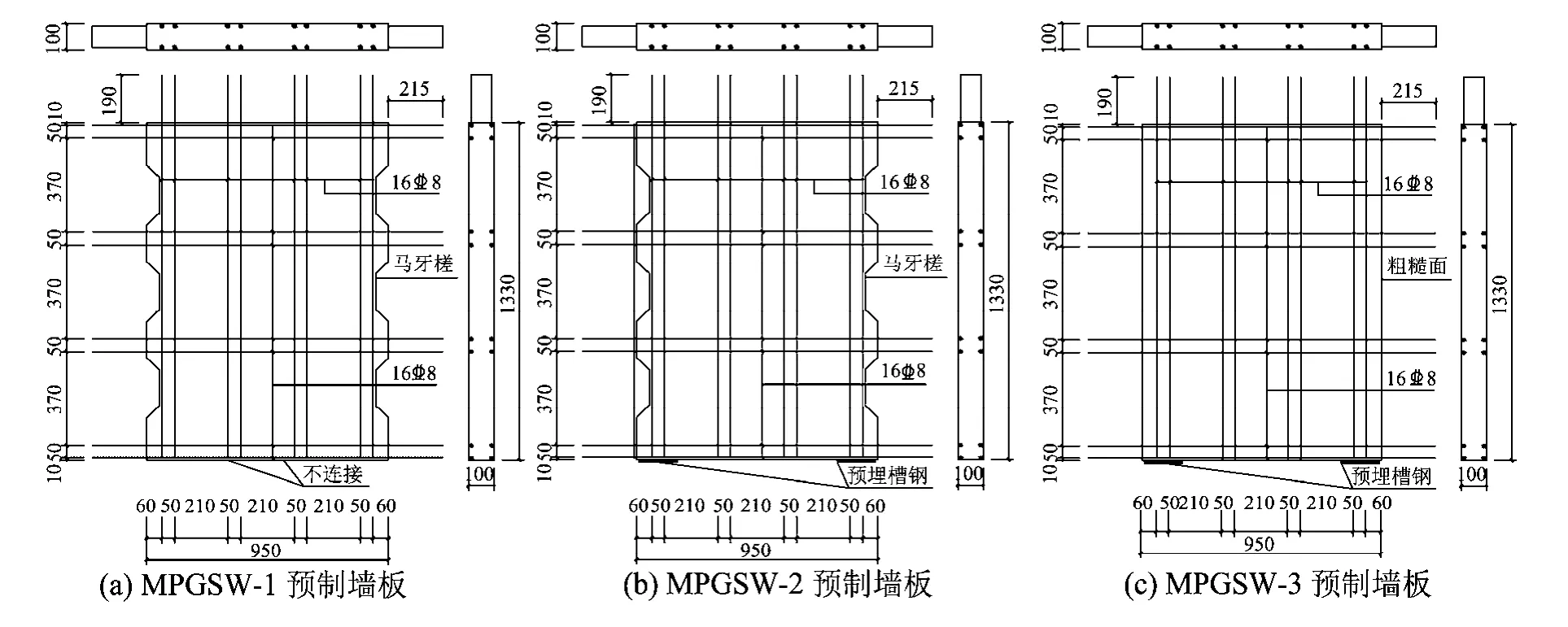
图1 试件尺寸及配筋Fig.1 Dimensions of specimens and arrangement of reinforcements

1.2 加载装置及方法

试验在西安建筑科技大学结构工程与抗震教育部重点试验室进行。试验加载装置如图2所示。试件的轴向荷载由液压千斤顶提供并保持恒定不变。水平荷载由1000 kN的MTS电液伺服水平作动器提供，通过增加钢板及两侧高强螺杆施加于墙体加载梁的预埋钢板处，加载点与加载梁中心位于同一水平线，作动器的另一端固定在反力墙上。加载方法采取力-位移混合加载制度，试件屈服前，采用力控制并以30 kN为级差循环一次；试件屈服后，采用位移控制，每级循环三次。

1.3 试验测量方案及布置

主要测量内容有：1)试件承受各级循环荷载及相应的位移值，荷载采用作动器内置的传感器进行采集，加载点位移采用滑动位移传感器(LVDT位移计)采集，见图3(a)；2)各层位移由编号为①~③位移传感器分别采集，见图3(a)；3)试件对角线方向的剪切变形，采用拉线位移计(编号为④~⑤)采集；在距墙底100 mm高处两侧各布置一个百分表(编号为⑥~⑦)，见图3(a)；4)预制墙板的水平、竖向分布钢筋，现浇竖向边缘构件受力纵筋、箍筋应变布置点分布见图3(b)~图3(e)。

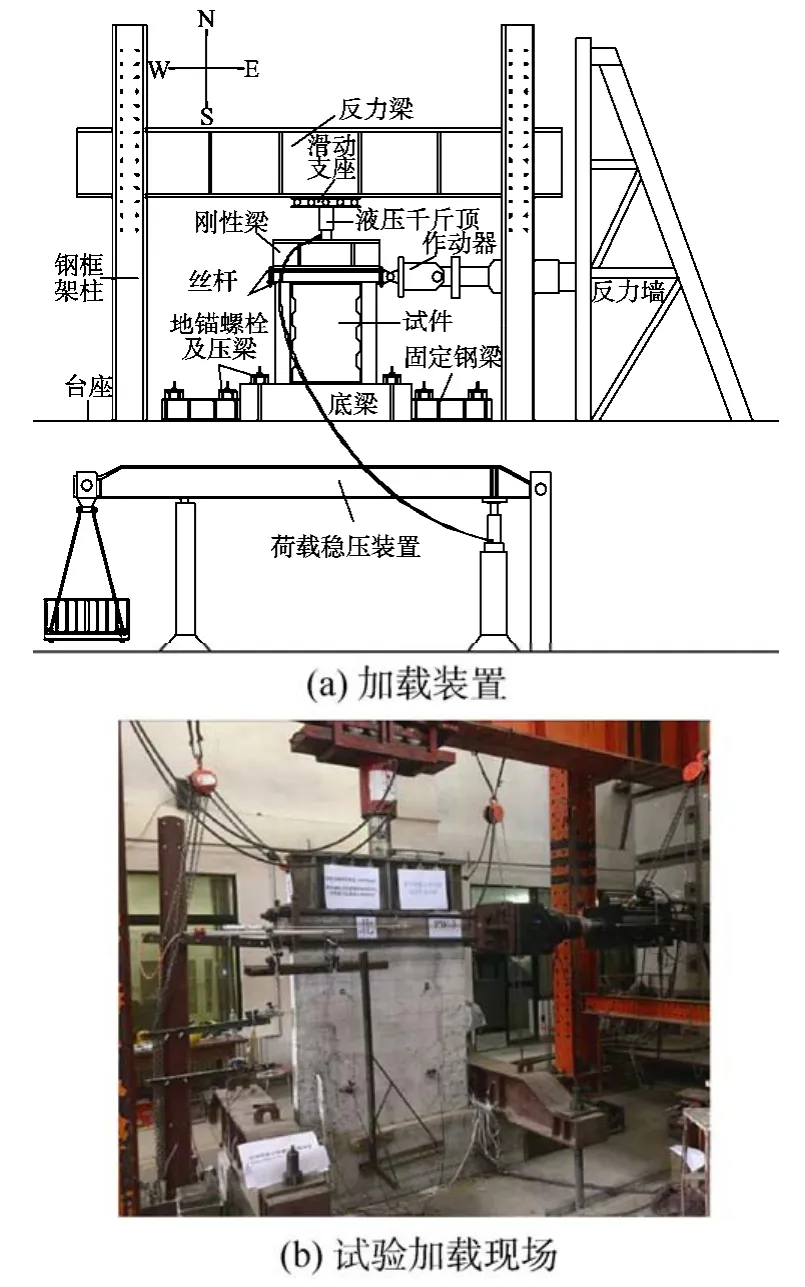
图2 加载装置示意图Fig.2 Diagram of test setup

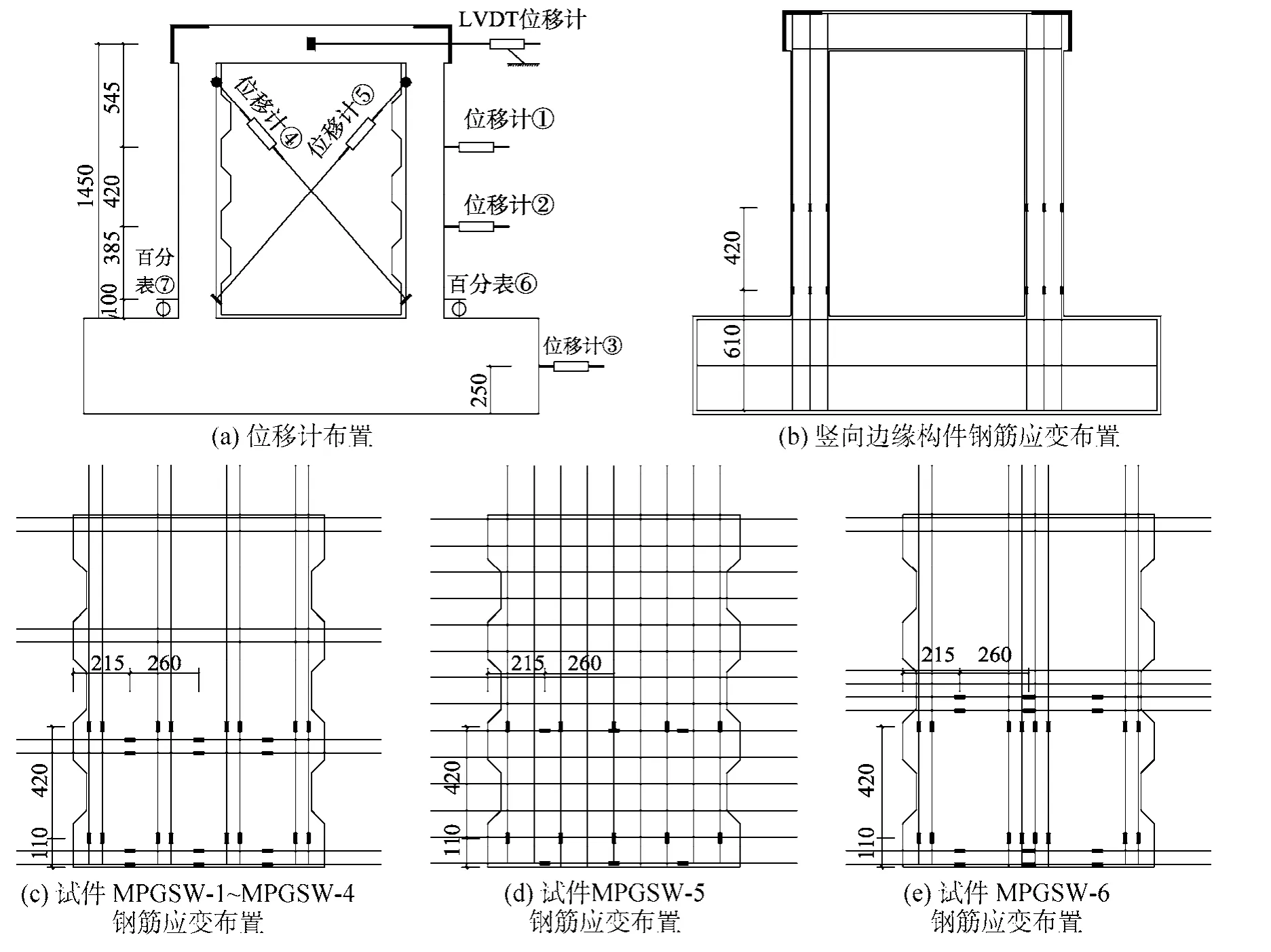
图3 测点布置Fig.3 Measuring points arrangement

1.4 试件破坏现象及形态

试件MPGSW-1~MPGSW-6的破坏过程与形态相似。最终破坏时，竖向边缘构件以水平弯曲裂缝为主，底部混凝土压碎脱落，钢筋压曲外露的弯曲破坏。由于试件MPGSW-1预制墙板内竖向钢筋底部未连接，墙板裂缝分布较少，坐浆层破坏严重；而采用预埋件焊接的试件MPGSW-2其预制墙板斜裂缝分布较为均匀，焊接部位无明显破坏，说明采用预埋焊板焊接能有效的传递钢筋应力，预制墙板与现浇边缘构件协同工作性能良好。对比不同竖向接缝形式试件可以看出：预制墙板采用马牙槎竖缝时，可有效避免裂缝沿着预制墙板与现浇边缘构件的拼缝形成从上而下的通缝，而采用粗糙面竖缝形式，竖向拼缝形成贯通裂缝，最大裂缝宽度达3 mm~4 mm；对比不同布筋方式试件可以看出：采用井字形布筋时，在内部形成以布筋区域的主结构和未布筋区域的次结构。破坏时次结构首先出现裂缝，随着裂缝开展及闭合，主结构开始破坏，因此，墙板内部裂缝分布比较均匀；而田字形布筋的是将预制墙板水平及竖向分布钢筋集中在沿墙板长、高度方向的中心，即在内部形成“十”字型，“十”字型的四角均为未布筋的素混凝土。试件破坏时，次结构的区域较大，该处的混凝土破坏及脱落较为严重，承载力下降较快。图4为6榀试件的最终破坏形态。

1.5 滞回曲线

6榀试件的滞回曲线如图5所示：可知MPGSW-1滞回环包围的面积较小，且峰值荷载和峰值位移也较小；而MPGSW-2滞回环所包围的面积较大，达到峰值荷载后，试件MPGSW-2随着加载位移的增大而仍继续荷载，其峰值荷载及位移分别提高6.78%和47.34%，说明预制墙板底部采用预埋焊板连接能较好地提高墙体的变形能力；对比不同竖向接缝形式可以看出：3榀试件的滞回环的形状、所包围的面积及演化趋势较为接近，其中采用马牙槎竖缝连接的试件MPGSW-2滞回性能相对较好，耗能及延性较优；对比不同预制墙板布筋方式可以看出采用井字型布筋方式的试件滞回曲线更为饱满，刚度及强度退化较为缓慢，具有较好的延性；传统配筋的试件MPGSW-5捏拢现象最为明显，MPGSW-6次之；MPGSW-6滞回环相比MPGSW-5滞回环更为饱满，延性更优。

1.6 骨架曲线

6榀试件骨架曲线见图6所示。由图6(a)可知：试件MPGSW-1骨架曲线的上升段斜率略高与试件MPGSW-2；随着荷载增加，骨架曲线下降段开始出现偏差，竖向钢筋未连接的试件MPGSW-1相比试件MPGSW-2下降更加陡峭。这是由于到了加载后期，预制墙板底部坐浆层破坏严重，钢筋未连接导致预制墙板与边缘构件的协同工作性能较差，承载力下降严重。由图6(b)可知：三榀试件的骨架曲线上升段基本重合；随着荷载增大，曲线的下降段陡峭度也比较接近，说明预制墙板竖向接缝形式对试件的骨架曲线影响不大。由图6(c)可知：采用井字形布筋方式的试件MPGSW-2其峰值荷载及位移最大，传统配筋形式的峰值荷载及位移略低；从曲线下降段陡峭度来看，试件MPGSW-2最为平缓，说明井字形布筋方式的试件变形能力最好；传统布筋方式的试件MPGSW-5下降段陡峭度最大，极限位移最小，破坏较为突然。

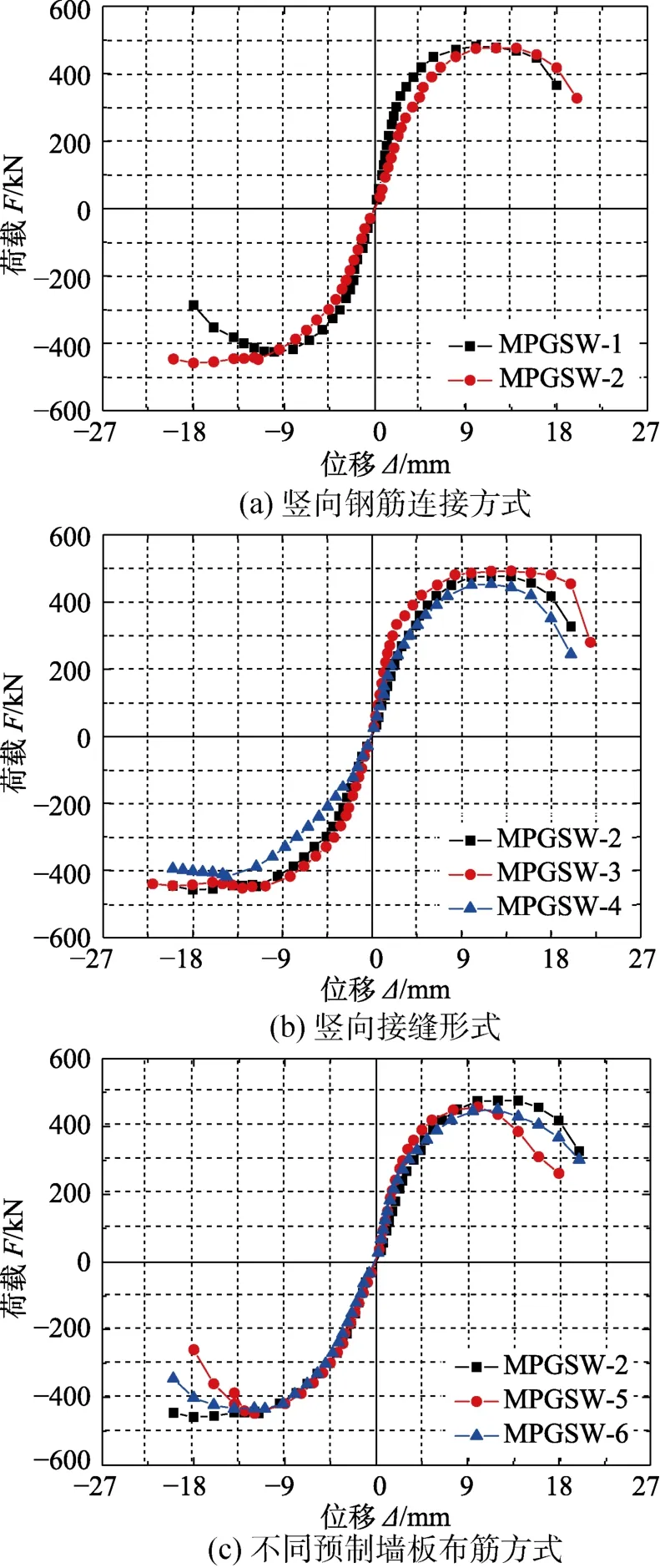
图6 试件骨架曲线Fig.6 Skeleton curves of specimens

2 压弯承载力计算

在弯矩M和轴力N共同作用下，6榀装配整体式网格剪力墙体可按偏心受压构件进行计算分析，考虑现浇边缘构件的影响，分别提出该墙体各阶段的正截面弯矩-曲率计算公式。

2.1 开裂弯矩Mcr和曲率φcr

加载初期，由于水平荷载较小，剪力墙底部截面产生的弯矩较小；随着荷载继续增大，在剪力墙的竖向边缘构件底部首先出现裂缝，随即发展成弯曲裂缝。造成裂缝的原因是剪力墙竖向边缘构件受拉区边缘混凝土在压-弯-剪共同作用下达到混凝土的开裂应变。以此作为墙体的开裂依据，对应的开裂弯矩为Mcr、开裂荷载为Fcr。图7为墙体底部开裂截面每一位置处实测平均应变沿墙体高度的分布图。可以看出：在开裂阶段，墙体截面应变分布符合平截面假定，个别墙体截面的受拉边缘纵筋应变有突增现象。

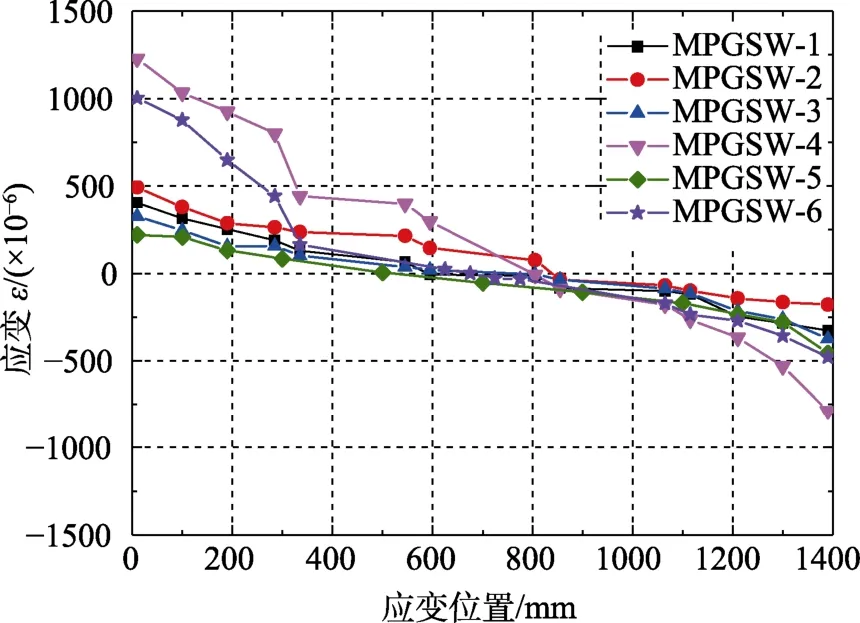
图7 开裂平均应变沿截面高度分布图Fig.7 Distribution of mean strain along section height at cracking state

当受拉区竖向边缘构件边缘混凝土应变达到开裂应变εtc时，剪力墙进入开裂阶段。此时，墙体的受力特点为：1)剪力墙截面受拉区混凝土应力呈曲线分布，为简化计算，按照等效原则，将受拉区混凝土应力图转换为三角形分布，其最外侧边缘混凝土应力取γft，γ=2；2)截面受压区最外侧混凝土的压应变εc<ε0，相应的压应力很小，尚处于弹性阶段，应力图形为三角形分布；不考虑边缘构件中箍筋的约束作用；3)考虑竖向边缘构件中拉、压纵筋的贡献；4)当预制墙板底部纵筋与底梁未形成可靠连接时，不考虑该竖向分布筋的贡献；当预制墙板底部纵筋与底梁形成可靠连接时，需考虑预制墙板内竖向分布筋的贡献，其应力按三角形分布计算。此时墙体截面应力、应变分布如图8所示。

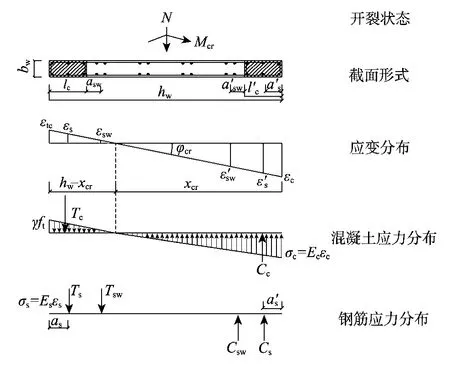
图8 截面开裂状态应变、应力分布图Fig.8 Stain and stress distribution of wall at cracking state

由截面应力图分布可得关系式：

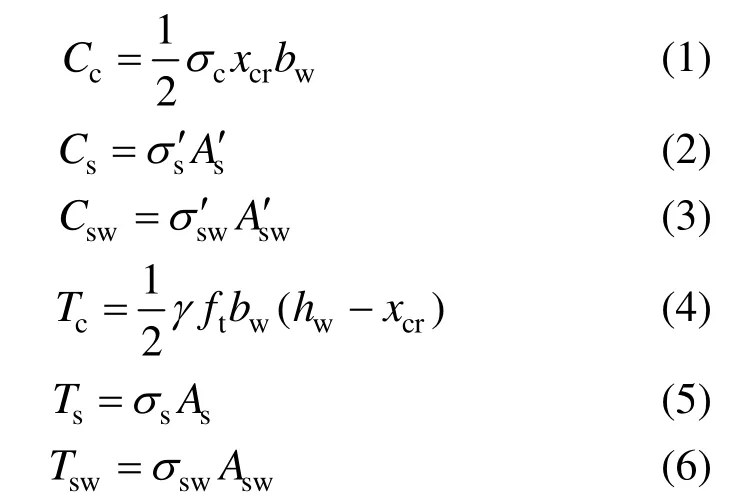
由截面应变图分布可得关系式：

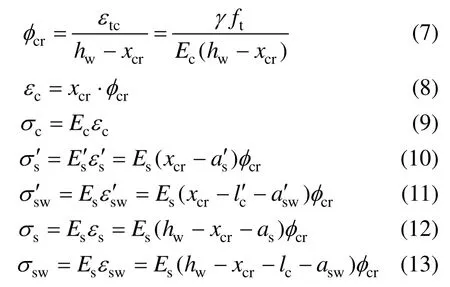
式中：xcr为开裂状态下墙体截面受压区高度；lc、为受拉、受压竖向边缘构件截面高度；as、分别为竖向边缘构件受拉、受压纵筋合力点至截面受拉、受压边缘的距离；asw、分别为预制墙板内受拉、受压纵筋合力点至预制墙板混凝土受拉、受压边缘的距离；εc为受压区边缘混凝土压应变；εs、分别为受拉、受压区纵筋拉、压应变；εsw、分别为预制墙板内受拉、受压区分布钢筋拉、压应变(对于底部钢筋未形成可靠连接，不考虑此钢筋对截面弯矩的贡献)；σc为受压区边缘混凝土应力；σs、为受拉、受压区纵筋应力；σsw、为受拉、受压区分布钢筋应力；Es为钢筋弹性模量；Ec为混凝土的弹性模量；γft为受拉区边缘混凝土等效应力；As、分别为受拉、受压区纵筋截面面积；Asw、分别为受拉、受压区分布钢筋截面面积；φcr为墙体截面的开裂曲率；Cc受压区混凝土合力；Cs为受压区边缘构件纵筋合力；Csw为受压区预制墙板分布钢筋合力；Tc受拉区混凝土合力；Ts为受拉区边缘构件纵筋合力；Tsw为受拉区预制墙板分布钢筋合力。

由截面应力分布及平衡条件可得：

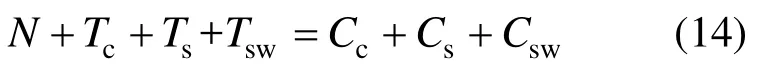
联立式(7)和式(14)，可求得墙体在屈服状态下截面受压区高度xcr和曲率φcr。

对墙体截面形心点取矩，可得截面开裂弯矩Mcr：

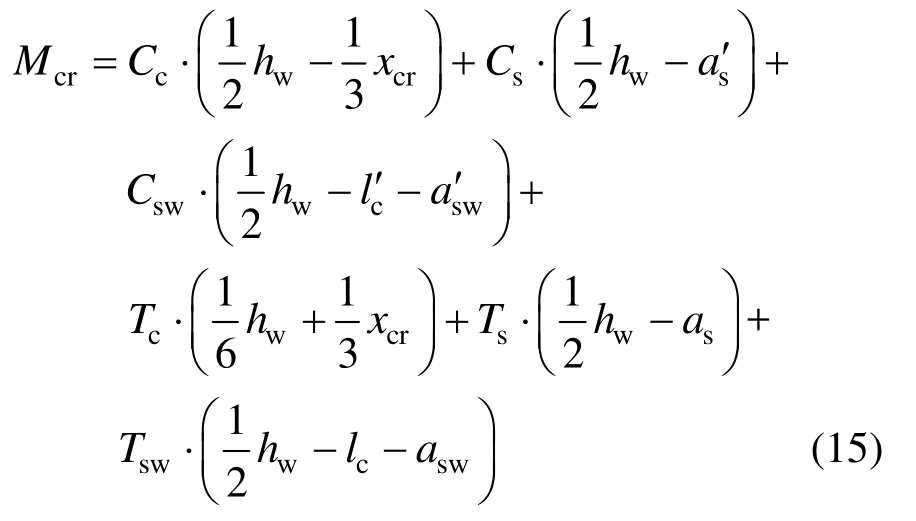
开裂荷载Fcr的计算表达式为：

式中，Hw为剪力墙底部至加载梁中心的距离。

2.2 屈服弯矩My和曲率φy

当墙体开裂后，剪力墙进入带裂缝工作阶段。继续加载时，墙身裂缝不断增加，刚度下降，墙体截面的中和轴不断向受压区偏移，相应的截面曲率也逐渐增大。当受拉区的纵向钢筋应变达到屈服应变εy时，以此为墙体的屈服依据，对应的屈服弯矩为My、屈服荷载为Fy。图9为屈服状态下墙体底部截面每一位置处实测平均应变沿墙体高度的分布图。可以看出：在屈服阶段，墙体截面应变分布仍满足平截面假定。

当受拉区的纵向钢筋应变达到屈服应变εy时，剪力墙进入屈服阶段。此时，墙体的受力特点为：1)截面受拉区大部分混凝土已开裂，仅有靠近中和轴附近的一小部分混凝土承受拉力，故不考虑受拉混凝土的作用；2)截面受压区混凝土的压应变εc＜ε0，相应的压应力很小，尚处于弹性阶段，应力图形仍为三角形分布；不考虑边缘构件中箍筋的约束作用；3)假定边缘构件内纵筋应力分布呈三角形分布，受拉纵筋达到屈服应力，受压纵筋应力按照σ＇s=Esε＇s来计算；4)当预制墙板底部纵筋与底梁未形成可靠连接时，不考虑墙板内竖向分布筋的贡献；当预制墙板底部纵筋与底梁形成可靠连接时，需考虑预制墙板内竖向分布筋的贡献，其应力按三角形分布计算。此时墙体截面应力、应变分布如图10所示。

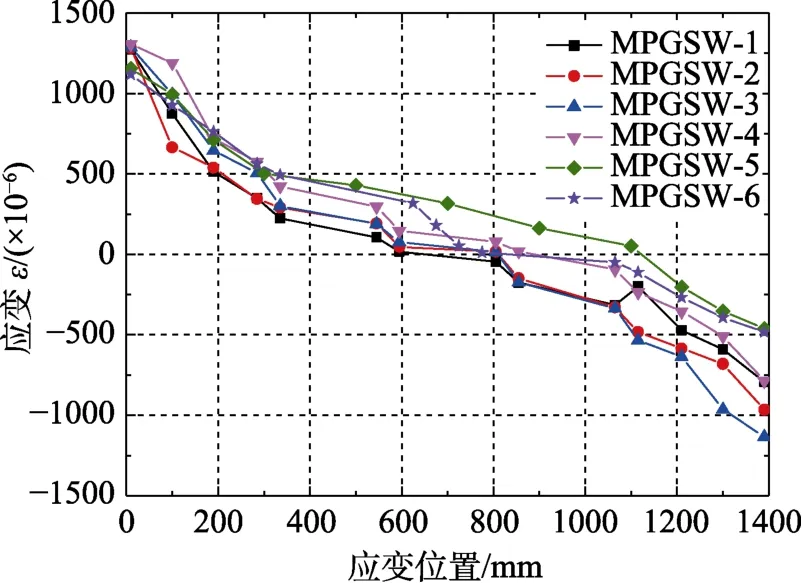
图9 屈服平均应变沿截面高度分布图Fig.9 Distribution of mean strain along section height at yielding state

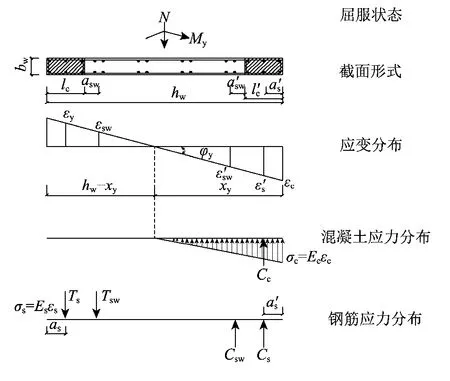
图10 截面屈服状态应变、应力分布图Fig.10 Stain and stress distribution of wall at yielding state

由截面应力图分布可得关系式：

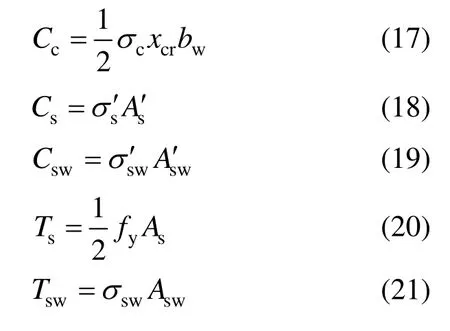
由截面应变图分布可得关系式：

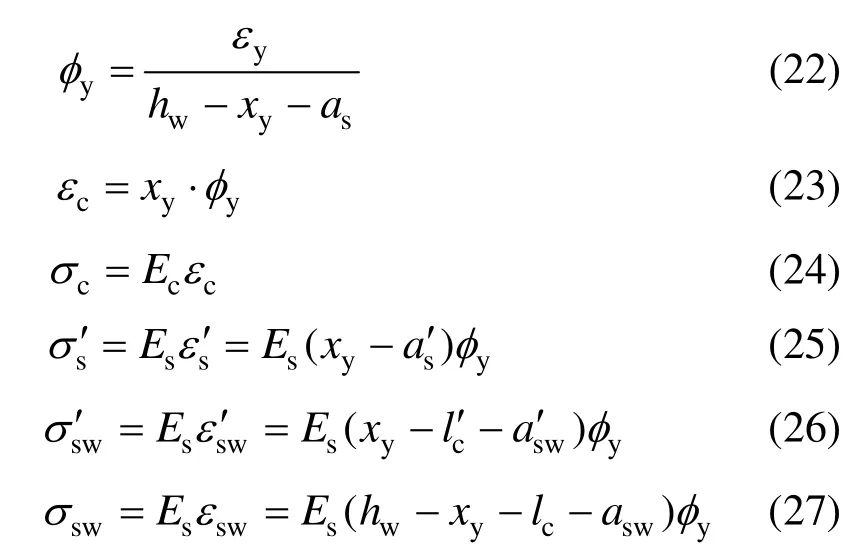
由截面应力分布及平衡条件可得：

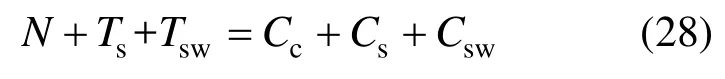
联立式(22)和式(28)，可求得墙体在屈服状态下截面受压区高度xy和曲率φy。

对墙体截面形心点取矩，可得截面屈服弯矩My：

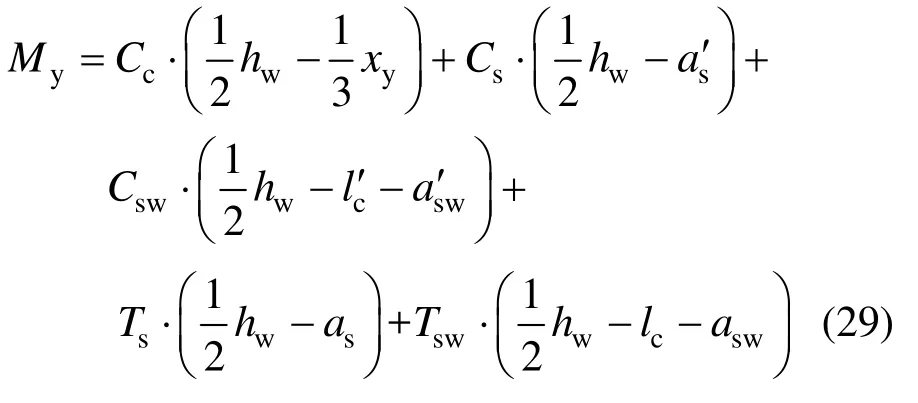
屈服荷载Fy的计算表达式为：

式中，Hw为剪力墙底部至加载梁中心的距离。

2.3 峰值弯矩Mp和曲率φp

当墙体受拉纵筋屈服后，继续增加荷载，受压区的混凝土应变增大。由于两端竖向边缘构件的存在，设置箍筋可提高混凝土的承载力及变形能力[14－15]，因此计算压弯承载力时需考虑箍筋对核心区混凝土的约束作用。当墙体的竖向边缘构件截面外侧的约束混凝土达到峰值压应变εcc(定义为约束混凝土应力下降至峰值应力 50%对应的应变ε0.5cc[16])，非约束区混凝土受压外侧应变达到混凝土峰值压应变ε0时(取ε0=0.002)，以此为墙体的峰值依据，对应的峰值弯矩为Mp、峰值荷载为Fp。图11为峰值荷载状态下墙体底部截面每一位置处实测平均应变沿墙体高度的分布图。可以看出：在峰值阶段，墙体两端竖向边缘构件内部纵筋应变出现梯度突变，而截面受拉端至非约束区受压外侧应变分布仍为线性分布，因此，可近似认为墙体的截面应变分布仍满足平截面假定。

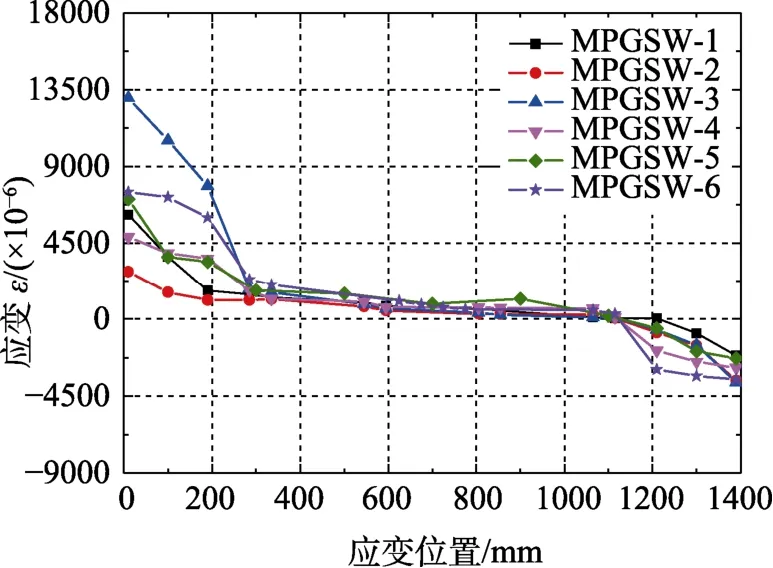
图11 峰值平均应变沿截面高度分布图Fig.11 Distribution of mean strain along section height at peak loading state

竖向边缘构件截面外侧的约束混凝土达到峰值压应变εcc，非约束区混凝土受压外侧应变达到混凝土峰值压应变ε0时，剪力墙进入峰值阶段，此时，墙体的受力特点为：1)当剪力墙进入峰值阶段，由于钢筋与混凝土之间黏结滑移变形影响逐渐增大[17]，导致两端竖向边缘构件内部纵筋应变出现梯度突变，截面应变分布不再符合平截面假定，但由于截面受拉端至非约束区受压外侧应变分布仍为线性分布，故近似认为墙体的截面应变分布仍满足平截面假定；2)受压区非约束混凝土应力呈曲线型分布，最大应力为fc，可用等效矩形应力图代替实际的混凝土压应力图形，等效矩形应力图形混凝土应力为α1fc，等效矩形应力图形高度为β1xp；受压区约束混凝土应力呈梯形分布，即约束混凝土内侧应力达到峰值应力fcc，外边缘应力约为0.5fcc[18]；不考虑受拉区混凝土的作用；3)在峰值状态下，拉、压边缘构件内部纵筋都已屈服，部分钢筋可能达到强化阶段(εs≥εsu)，为简化计算，边缘构件内部纵筋取屈服强度fy；4)在峰值状态下，只考虑受拉区底部有可靠连接的分布钢筋受拉作用，根据试验结果可知，分布钢筋应力达到屈服强度fyw，受压区竖向分布筋受力较小尚未屈服，为简化计算不予考虑。

边缘构件约束混凝土峰值应力fcc可采用下式进行计算[19－20]：

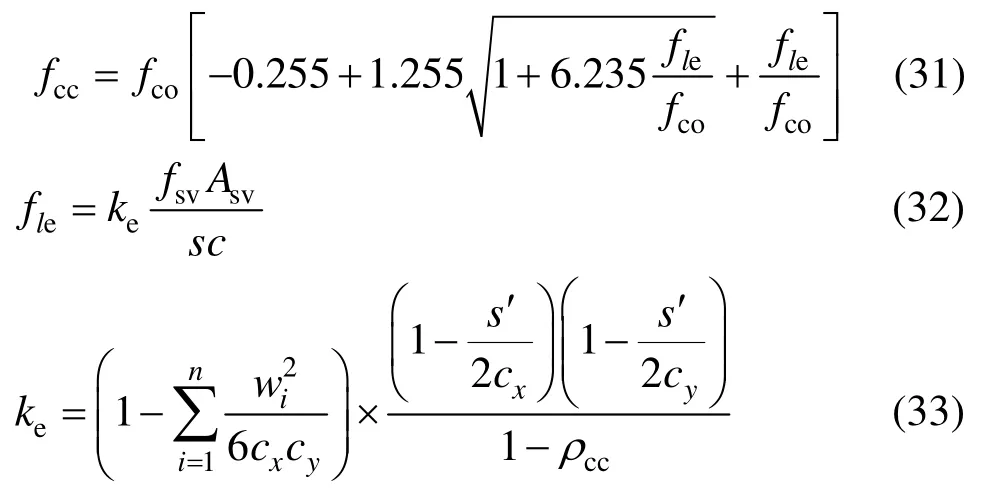
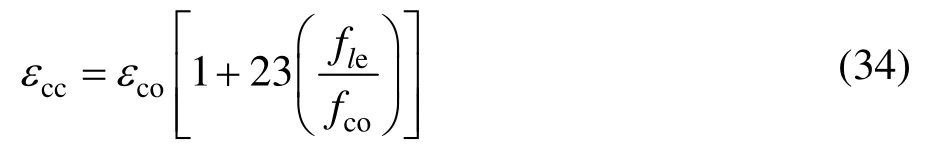
式中：fco为非约束区混凝土峰值应力；fle为约束混凝土达到峰值强度时箍筋的有效侧向约束力；ke为有效约束系数，综合反映了箍筋形状、纵筋分布和截面尺寸对约束效果的影响[21]；fsv为约束混凝土达到峰值时对应的箍筋应力；Asv为箍筋各肢在截面边长方向投影面积之和，对于矩形箍Asv取2倍单肢箍面积；s为箍筋间距；s＇为箍筋净间距；c为边缘箍筋中心间距；wi为相邻纵筋净距；cx为x方向边缘箍筋中轴线之间的距离；cy为y方向边缘箍筋中轴线之间的距离；ρcc为边缘构件纵筋配筋率；εcc为约束混凝土的峰值应变；εco为非约束区混凝土的峰值压应变。

此时墙体截面应力、应变分布如图12所示。

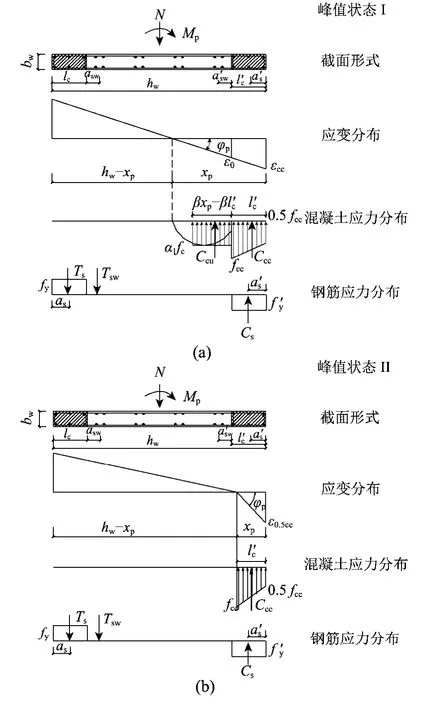
图12 截面峰值状态应变、应力分布图Fig.12 Stain and stress distribution of wall at peak loading state

1)当xp≥时(即受压区高度大于边缘构件高度时)，由图12(a)中截面应力图分布可得关系式：

由截面应力分布及平衡条件可得：

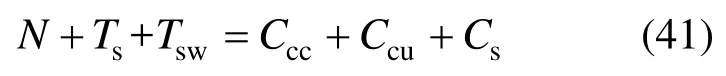
根据式(40)、式(41)，可求得墙体在峰值状态下截面曲率φp和受压区高度xp。

对墙体截面形心点取矩，可得截面峰值弯矩Mp：

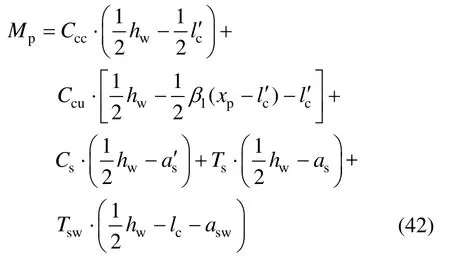
2)当xp＜时(即受压区高度小于边缘构件高度时)，由图12(b)中截面应力图分布可得关系式：

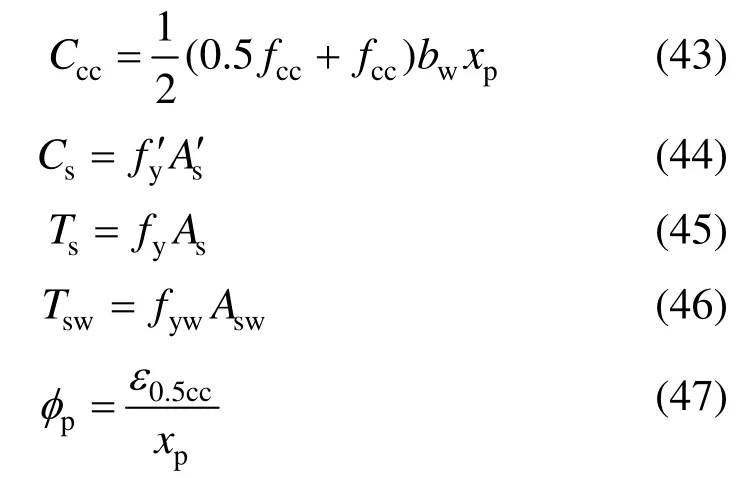
由截面应力分布及平衡条件可得：

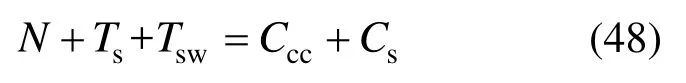
根据式(47)、式(48)，可求得墙体在峰值状态下截面曲率φp和受压区高度xp。

对墙体截面形心点取矩，可得截面峰值弯矩Mp：

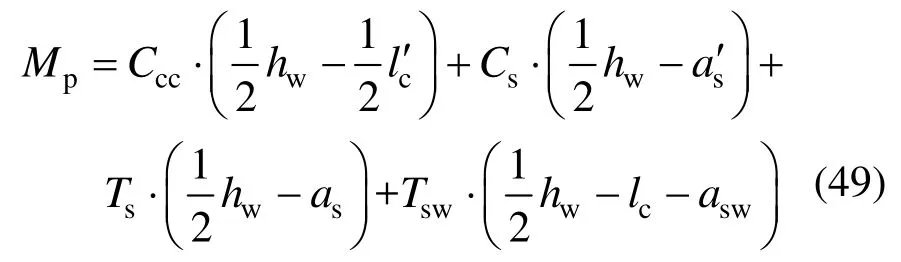
峰值荷载Fp的计算表达式为：

2.4 破坏弯矩Mu和曲率φu

继续增加荷载至峰值荷载Fp的 85%，此时，受压区约束混凝土的应变达到极限压应变εccu，非约束区混凝土受压混凝土达到极限压应变εcu时，以此为墙体的破坏依据，对应的破坏弯矩为Mu、破坏荷载为Fu。

此时，墙体的受力特点为：1)截面应变分布不再符合平截面假定，但受压区应变可仍按线性分布来计算；2)受压区非约束混凝土达到极限压应变εcu(本文εcu取0.0033)，受压区约束混凝土达到极限压应变εccu，其值按式(51)来确定[22]；3)截面变形较大，不考虑混凝土的受拉作用；4)受拉区的竖向边缘构件纵筋及墙板内可靠连接分布钢筋均已屈服，甚至可能强化或拉断；受压区纵筋及连接钢筋全已受压屈服。

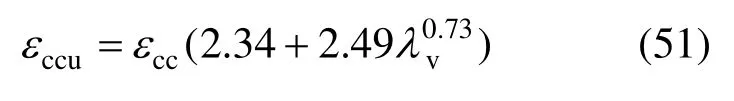
根据以上分析，墙体破坏弯矩Mu=0.85Mp，破坏荷载Fu=0.85Fp；破坏曲率φu取墙体受压边缘压应变达到极限压应变εccu所对应的截面曲率。试验表明，在破坏状态下，墙体截面受压区高度xu与峰值状态下的墙体截面受压区高度xp基本保持相同，即：

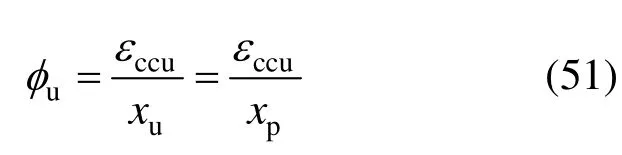
2.5 计算结果与试验结果对比

表2和表3为墙体在各阶段的水平荷载、曲率计算值与试验值的对比。结果表明：在开裂阶段，由于考虑两侧竖向边缘构件纵筋及预制墙板内可靠连接的分布筋对开裂弯矩的贡献，因此，计算出的开裂荷载与试验值较为接近。预制墙板竖向钢筋连接方式、竖向接缝形式、布筋方式对墙体的开裂荷载影响较小；试件MPGSW-2~MPGSW-4的开裂曲率计算值大于试验值，这是由于混凝土材料的离散性以及开裂状态是在加载过程中由肉眼所确定，确定方法较为粗略而导致。

对于屈服状态，试件的屈服荷载和曲率计算值与试验值吻合较好，误差控制在10%以内，验证了在装配整体式网格剪力墙中采用“最远点法”确定屈服荷载的准确性[23－24]。

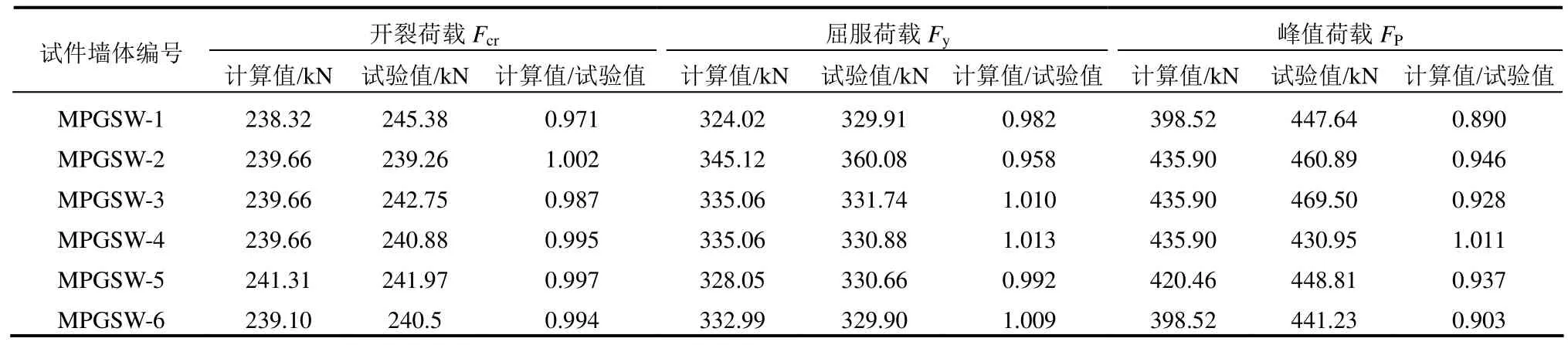
表2 各阶段荷载计算值与试验值对比Table 2 Comparison between calculated values and test values of load

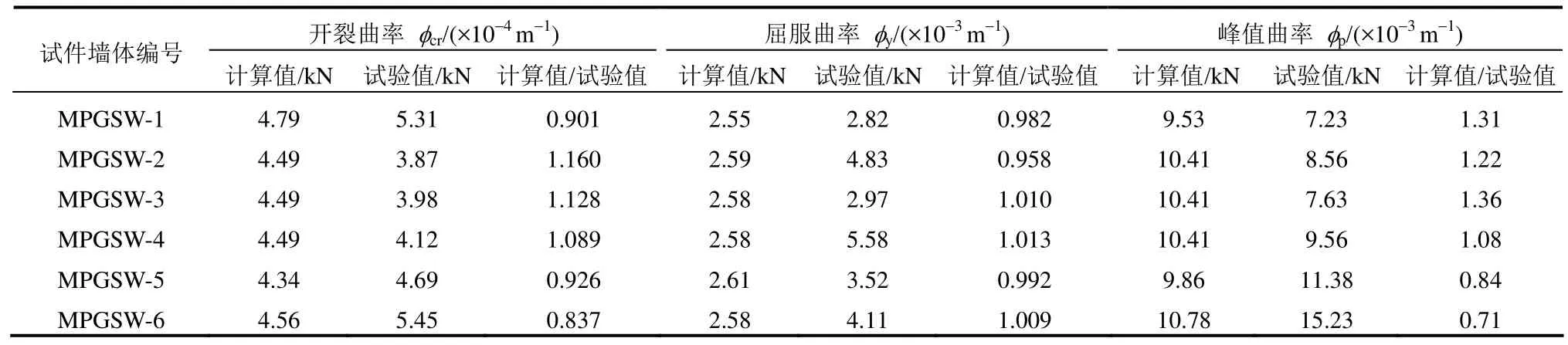
表3 各阶段墙体截面曲率计算值与试验值对比Table 3 Comparison between calculated values and test values of curvature of specimens

对于峰值状态，由于考虑两侧竖向边缘构件箍筋对混凝土的约束作用，计算值与试验值吻合较好，计算值大致偏小，较为安全；在预制墙板内分布钢筋底部设置预埋件焊接时，墙体的峰值荷载可提升10%；预制墙板竖向接缝形式对墙体的峰值荷载无影响；预制墙板布筋方式对墙体的峰值荷载有一定影响，总体表现为采用井字形布筋方式墙体的峰值荷载最高，而采用田字形布筋方式墙体的峰值荷载较低。本文建立的峰值荷载计算公式与实测结果吻合较好，满足设计要求。

在峰值阶段，墙体截面曲率计算值与试验值有一定的偏差，表现为随着预制墙板竖向钢筋由不连接变成预埋件焊接，峰值曲率随即增大；竖向接缝形式及预制墙板布筋方式对墙体峰值曲率影响不大。

3 结论

本文对不同阶段装配整体式网格剪力墙压弯承载力计算分析，得到以下结论：

(1)6榀试件破坏形态相似，均发生以竖向边缘构件水平弯曲裂缝为主，底部混凝土压碎脱落，钢筋压曲外露的弯曲破坏。

(2)基于平截面假定，充分考虑预制墙板可靠连接钢筋作用，忽略未连接钢筋作用，建立墙体在开裂、屈服状态弯矩-曲率的计算方法，计算结果与试验值吻合较好，说明所提出的计算方法较为合理。

(3)考虑边缘构件箍筋对混凝土的约束作用，并引入等效矩形应力图形系数，建立墙体在峰值状态的弯矩-曲率计算方法，计算值偏小于试验值，较为安全。

(4)预制墙板内分布钢筋连接方式是影响墙体峰值荷载和曲率的重要因素。当预制墙板底部设置预埋件焊接时，墙体峰值荷载可提高10%；竖向接缝形式对墙体的峰值荷载和曲率无影响；布筋方式对峰值荷载影响表现为井字形布筋方式墙体的峰值荷载最高，田字形布筋方式墙体的峰值荷载较低；布筋方式对峰值曲率影响较小。