基于灰色理论的交通事故多发点段评价模型

张朝旭

（中国刑事警察学院痕迹检验技术系，辽宁 沈阳110035）

随着经济的发展和人民生活水平的提高，车辆的数量和种类越来越多，几乎成为家庭生活中的必需品。一方面，它给生活带来了极大的便利，增加了生活中的乐趣和效率；另一方面，它也给道路交通施加了很大的压力，出现了道路拥堵、交通事故频发等问题。在资源有限的条件下，如何有效地减少交通事故的发生成为当今社会亟需解决的问题。

目前，道路交通事故多发点段的研究大多集中在事故多发点段的鉴别、预防和其主要成因分析等方面，对其等级划分和治理的紧迫性研究尚少。卢辉忠等提出对排查得出的事故多发点段进行等级评定，根据等级大小排序进行分批治理［1］；刘敏等在对交通事故资料和事故多发点段主要成因分析的基础上，确定了一套多发点段治理的定量和定性指标，并建立了治理排序模型［2］；符锌砂等提出基于BP神经网络的方法对事故多发点段的治理紧迫性进行研究，建立了4个一级指标和6个二级指标的事故多发点段治理评价体系，最后并用实例验证了该评价体系的可靠性［3］；李嘉运用地理信息系统将MapX技术与Visual Basic语言相结合，设计出事故多发点段智能识别模型，并提出了事故多发点段治理迫切度的概念，最后通过构建神经网络优化求解出事故多发点段的治理迫切值［4］；许林新等提出了基于层次分析的道路交通事故多发点段的评价方法，构建了基于速度标准差、平均速度和速度标准差系数的评价指标体系［5］；毕和政等运用组合赋值和灰色聚类相结合的方法对公路平面交叉口的评价进行研究，最终将交叉口安全水平划分为5个等级，并通过实例验证该评价方法能够反映其实际安全状况［6］；温惠英等对山区公路交通事故多发点段进行研究，建立了基于当量总事故数的事故多发点段鉴别模型，并根据各点段计算出的结果对危险度进行划分，最后利用层次分析法判断事故多发点段主要成因的各指标权重［7］。

本文在确定交通事故多发点段的基础上，利用事故多发点段的信息，提出的基于灰理论对交通事故多发点段进行评价的方法是一种模糊聚类分析方法，能够有效地处理事故多发点段的治理先后问题。本文研究了事故多发点段的评价指标，建立了基于灰色关联分析的道路交通事故多发点段评价模型，并用具体的实例对模型进行了验证。

1 评价指标的确定

交通事故的发生具有一定的偶然性和必然性，是人、车、路、环境相结合的动态系统［8］，一旦发生交通事故，必然会对双方造成损害。能够反映一个事故多发点段影响程度和范围的因素有很多，但主要是死亡人数、受伤人数、事故数和财产损失四个指标。

死亡人数指标真实反映了事故多发点段的危险程度，交通事故中有人员死亡会对社会和家庭造成极大的伤害；受伤人数指标反映事故多发点段易造成伤害程度，虽然没有人员死亡，但是也会给人心理造成伤害，所以也把这个因素作为评价交通事故多发点段的指标；事故数是反映交通事故多发点段的主要指标，本论文的目的就是减少交通事故发生的次数，所以事故数是评价交通事故多发点段不可缺少的指标；财产损失指标是反映交通事故多发点段对人们生活品质的影响，在交通事故中，财产损失相比较来说对社会和家庭的影响较小，但仍然不是可以忽略的因素。评价指标的确定和原因如表1所示。

表1 评价指标的确定和原因

2 灰色关联分析

灰色系统理论是邓聚龙教授在1982年创立的，它是一种研究少数据、贫信息不确定性问题的新方法。该理论以“部分信息已知，部分信息未知”的“小样本”、“贫信息”不确定性系统为研究对象，主要通过对部分已知信息的生成、开发，从而提取有价值的信息，实现对系统运行行为、演化规律的正确描述和有效监控。灰色系统理论包含灰色关联分析、灰色聚类评估和灰色系统预测等多方面内容，本文选择采用灰色关联分析对道路交通事故多发点段进行等级评价。

灰色关联分析的基本思想是根据序列曲线几何形状的相似程度来判断其联系是否紧密。灰色关联分析方法弥补了采用数理统计方法进行系统分析所导致的缺憾，它对样本量的多少和样本有无规律都同样适用，而且计算量小，十分方便，更不会出现量化结果与定性结果不符的情况。灰色关联分析包含灰色绝对关联度、灰色相对关联度和灰色综合关联度。

设系统行为序列：

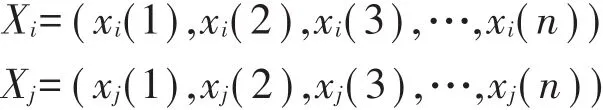
2.1 灰色绝对关联度的求值

求灰色绝对关联度，先求两序列的均指像，D为均值化算子。

则Xi与Xj的灰色绝对关联度为：

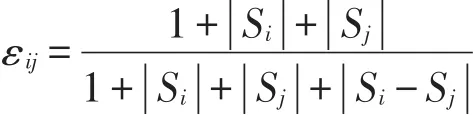
3 交通事故多发点段评价模型

2.2 灰色相对关联度的求值

求两序列的灰色相对关联度，先求两序列的初值像，D2为初值化算子。

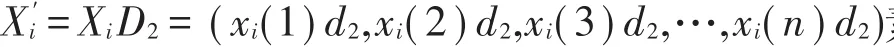
所以有：

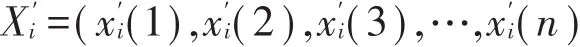
再求的始点零化像，D3为始点零化算子。

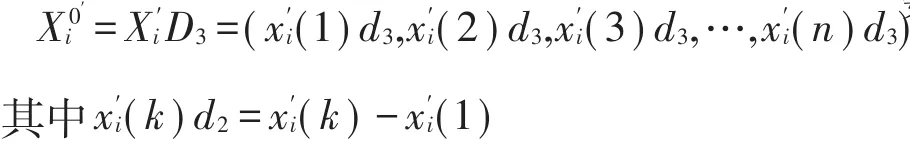
求得两序列的始点零化像记为：

2.3 灰色综合关联度的求值

灰色综合关联度既体现了折线Xi与Xj的相似程度，又反映出Xi与Xj相对于始点的变化速率的接近程度，是较为全面地表征序列之间联系是否紧密的一个数量指标。

灰色综合关联度的计算公式为：

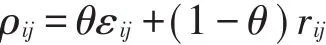
其中ρij表示灰色综合关联度，且0＜ρij≤1；εij表示灰色绝对关联度；rij表示灰色相对关联度；θ一般取0.5。

目前，交通事故多发点段的评价有事故数法、事故率法和概率论——数理统计法等方法。这些方法在一定程度上也能对事故多发点段进行评价排序，但是存在一定的缺陷，考虑的因素过于单一，所导致后期的点段治理效果不明显。灰度关联分析方法充分利用死亡人数、受伤人数、事故数和财产损失因素，对交通事故多发点段的评价更加合理和准确。

3.1 关联度的计算

对多个交通事故多发点段进行评价排序，考虑利用各个点段的各项指标构成的序列与总数据序列的接近程度。

用灰色序列表示为：

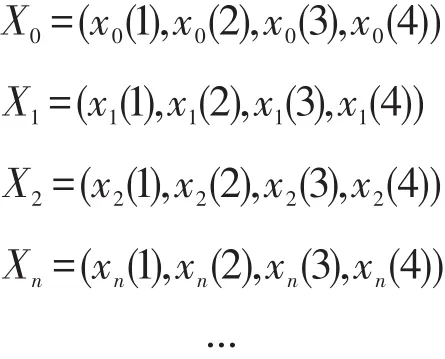
其中总数据序列表为：

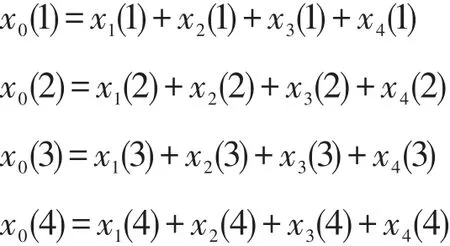
X1、X2...Xn表示n个交通事故多发点段；各个点段序列内的数值分别表示死亡人数、受伤人数、事故数和财产损失（万元）。

根据上面列出的灰色关联分析公式分别计算出各个事故多发点段序列与总数据序列的灰色绝对关联度ε和灰色相对关联度r，然后根据ρ=θε+(1-θ)r计算出灰色综合关联度ρ，θ取0.5。

3.2 事故多发点段的评价排序

计算出各个事故多发点段序列与总数据序列的灰色综合关联度之后，再考虑到评价区域内的交通状况和特点，以及治理事故多发点段的资金预算，取在结果范围内的两个不同的临界值a和b（a＜b），把要评价的交通事故多发点段分成三级。ρ具体的取值范围和等级描述如表2所示。

表2 ρ具体的取值范围和等级描述

交通事故多发点段的等级划分给当地部门对路段的治理，提高道路安全性提供了依据。根据划分好的等级，在资源有限的条件下优先治理三级事故多发点段，二级事故多发点段治理优先于一级事故多发点段的治理，也可以根据计算的数值把所有要评价的事故多发点段进行排序治理。后期根据计算的数值和等级划分分析造成交通事故频发的原因，以此找出解决问题的方法。

4 实例验证

对某市内已确定的25处交通事故多发点段进行评价排序，分别统计出各个事故多发点段近三年关于死亡人数、受伤人数、事故数和财产损失的详细数据。2015～2017年某市内25处交通事故多发点段统计资料如表3所示。

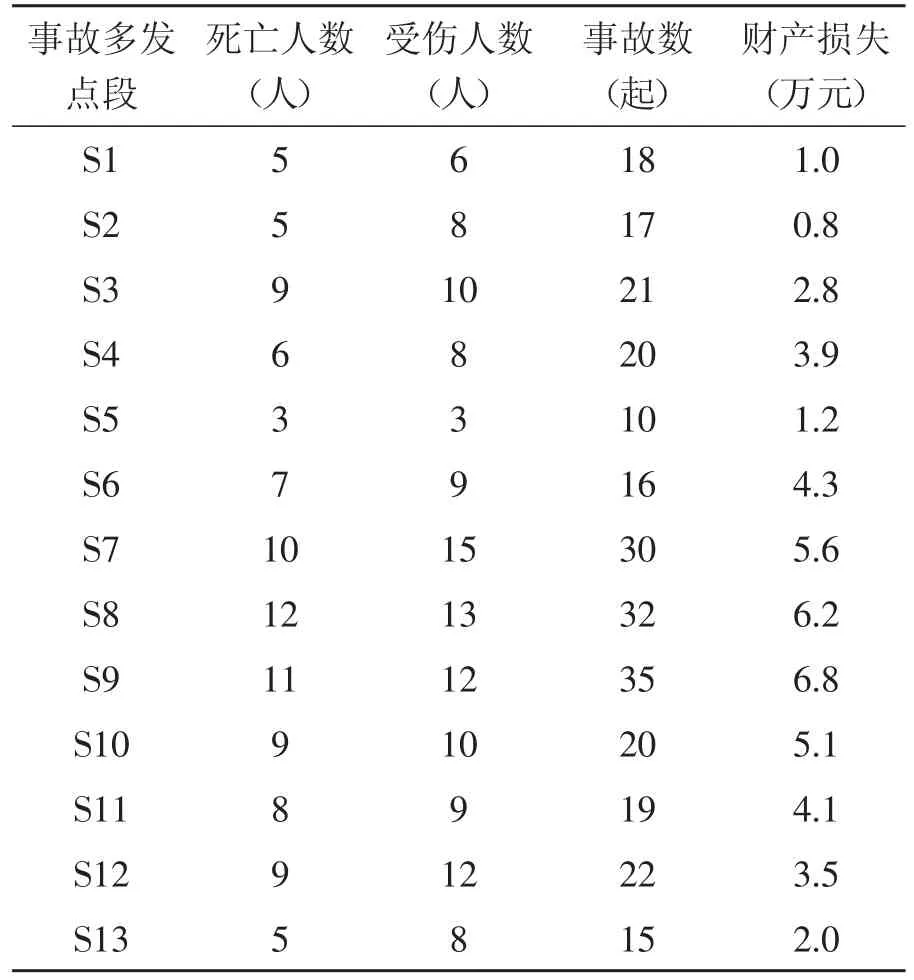
表3 2015～2017年事故多发点段处数据统计

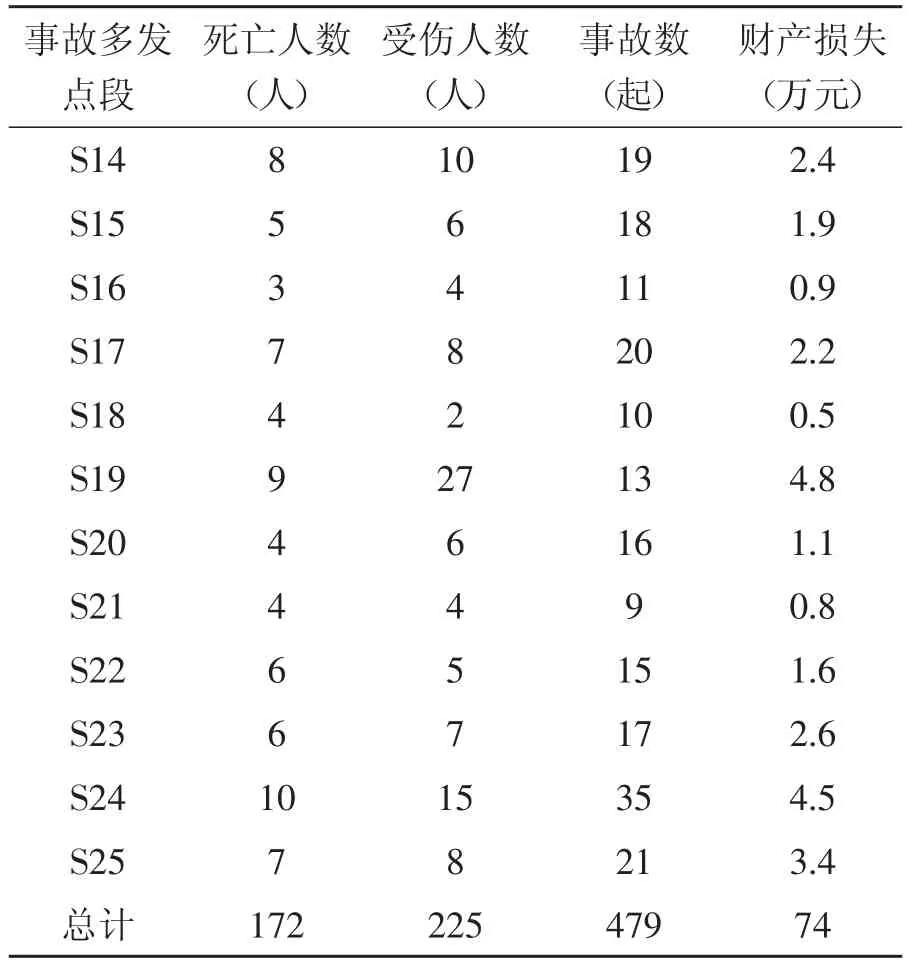
事故多发点段死亡人数（人）受伤人数（人）事故数（起）财产损失（万元）S14 S15 S16 S17 S18 S19 S20 S21 S22 S23 S24 S25总计8 5 3 7 4 9 4 4 6 6 1 10 6 4 8 2 2 0 7 7 6 4 5 7 1 5 8 172225 19 18 11 20 10 13 16 9 15 17 35 21 479 2.4 1.9 0.9 2.2 0.5 4.8 1.1 0.8 1.6 2.6 4.5 3.4 74

4.1 灰色综合关联度的求值

2015～2017年，在全市25个事故多发点段处总的死亡人数、受伤人数、事故数和财产损失分别为172人、225人、479起和74万元。则系统行为序列为：

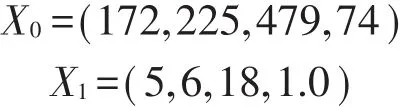
由以上所给的计算公式可以分别计算出序列X0和X1的灰色绝对关联度ε01、灰色相对关联度r01和灰色综合关联度ρ01。同理，可以计算出另外24个事故多发点段序列与总数据序列的关联度数值。各个事故多发点段序列与总数据序列的关联度计算结果如表4所示。

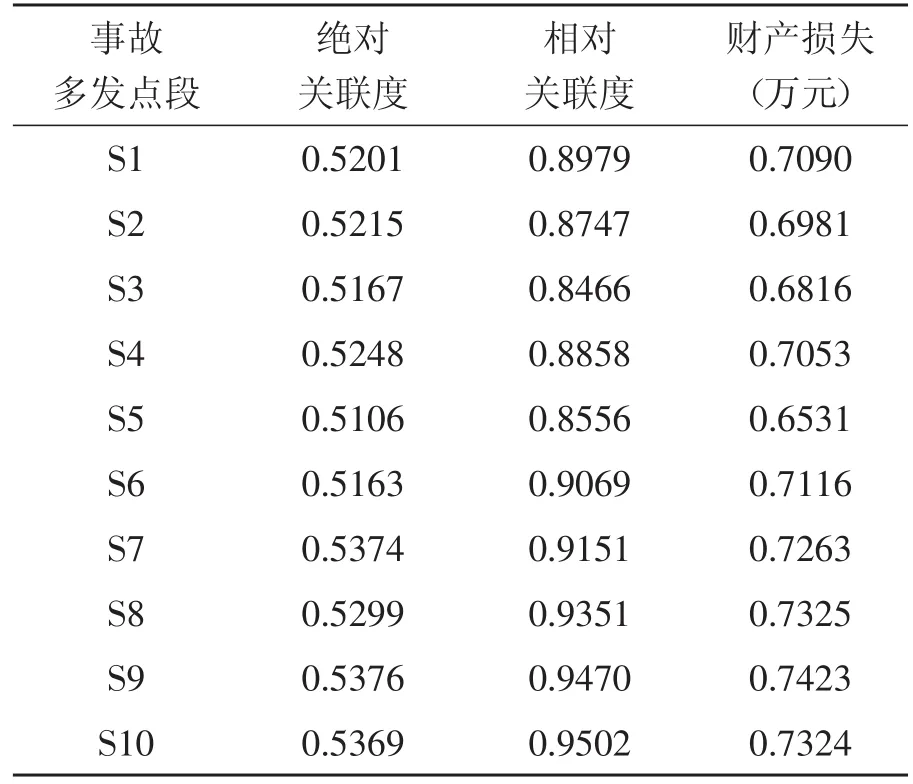
表4 关联度计算结果

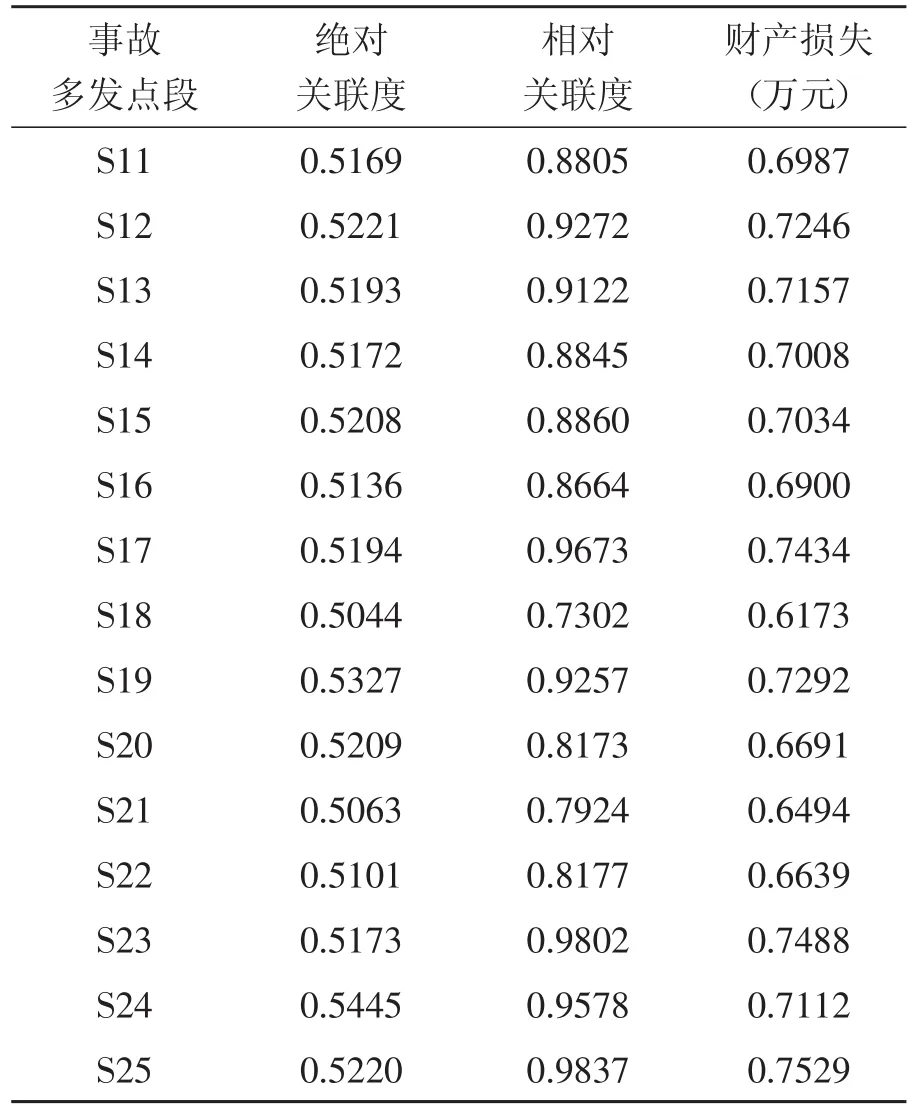
事故多发点段绝对关联度相对关联度财产损失（万元）S11 S12 S13 S14 S15 S16 S17 S18 S19 S20 S21 S22 S23 S24 S25 0.5169 0.5221 0.5193 0.5172 0.5208 0.5136 0.5194 0.5044 0.5327 0.5209 0.5063 0.5101 0.5173 0.5445 0.5220 0.8805 0.9272 0.9122 0.8845 0.8860 0.8664 0.9673 0.7302 0.9257 0.8173 0.7924 0.8177 0.9802 0.9578 0.9837 0.6987 0.7246 0.7157 0.7008 0.7034 0.6900 0.7434 0.6173 0.7292 0.6691 0.6494 0.6639 0.7488 0.7112 0.7529

4.2 事故多发点段的评价

根据全市道路的交通状况和特点，取a=0.6900,b=0.7200。根据表2的等级划分范围和表4的各个事故多发点段的综合关联度计算结果，事故多发点段的评价结果如下：

一级交通事故多发点段有S3，S5，S16，S18，S20，S21，S22。

二级交通事故多发点段有S1，S2，S4，S6，S11，S14，S15，S24。

三级交通事故多发点段有S7，S8，S9，S10，S12，S13，S17，S19，S23，S25。

5 结语

本文研究了交通事故多发点段的评价指标，然后通过考虑事故多发点段上的总事故数、死亡人数、受伤人数和财产损失四项指标，建立了基于灰色系统理论中的灰色关联分析的道路交通事故多发点段评价模型，并且通过确定临界点的方式，把交通事故多发点段分为三级。最后通过具体的实例对模型进行了检验，证明了其模型的可行性。

当然，本文也存在一些问题，临界值需要根据各地的交通状况和特点以及治理资金的预算来确定，没办法给出一个全国标准，以后还需要更加深入的研究，不断完善此评价模型。