基于SOM-RBF神经网络的用电量预测模型研究

毛锦伟，梁 甲，张修文

(1.防灾减灾湖北省重点实验室(三峡大学)，湖北 宜昌 443002；2.三峡大学 土木与建筑学院，湖北 宜昌 443002)

0 引言

随着我国经济的高速发展，电力建设需求也日益提升，“十三五”期间，经济发展步入新常态，经济增长的结构、动力等发生深刻变化，这对电力市场发展产生深远影响。电力发展是衡量一个国家经济水平的重要因素之一，对用电量的精准预测有利于电力企业合理安排经营计划，提高经济效益[1]。在电力发展改革中，对新兴智能技术的要求也不断提升，智能电网是电力工业发展的方向和趋势[2]。用电量预测是保证电力规划实施运行的基础，只有合理采用有效预测模型才能得到精确的结果，从而保证电力规划的经济性、合理性及适用性[3]。因此，如何保证用电量精准预测，有效建立合理化模型成为重中之重。

目前对于用电量模型的预测方法通常为传统的单耗法、弹性系数法、趋势外推法、主成分回归分析预测法、最小二乘回归预测法、灰色预测法、各类神经网络预测法和时间序列分析预测法等[4]。在传统神经网络分析方法中，BP神经网络是人工神经网络中的一个重要分支，已经在用电量预测研究中取得了广泛应用。然而，BP神经网络属于全局逼近网络，每给定网络一个输入，各个权值都需要调整，这将影响每个输出，从而导致其学习的速度是一个较慢的过程。BP网络是否达到收敛是与训练样本的容量大小、算法、网络结构、期望误差和训练步数等诸多方面都有很大的关系。

传统BP神经网络在用电量预测应用中出现的样本数量缺乏和网络结构确定的问题，难以准确预测，为了更好提升预测模型的精度，针对上述问题，引入SOM神经网络(Self-Orga-nizing Feature Map，SOM)[5,6]。先对整体样本进行自动聚类，再根据相似聚类结果分别建立RBF预测模型。RBF神经网络与BP神经网络相比，具有预算速度更快，而且不易陷入局部最小点优点，所以选用RBF神经网络对样本进行建模和预测。

为了避免由于训练样本点分散所导致的预测精度降低，采用先聚类、再分类建模和预测的方法。本文利用Matlab平台建立SOM-RBF混合算法，构成组合人工神经网络，在评测样本有限且训练样本点分布不均匀的情况下，得到更高的预测精度，实现对湖北省年用电量的精准预测。

1 SOM-RBF神经网络研究

1.1 SOM和RBF神经网络原理

1.1.1 SOM神经网络

SOM自组织特征映射网络(Self-organizing Feature Map，SOM)，也称Kohonen网络，由荷兰学者Teuvo Kohonen在1981年提出。SOM 网络的神经元是全连接的，该网络不仅能够学习输入量的分布特点，还能够学习输入量的拓扑结构。通过训练，可以建立起这样一种布局，它使得每个权值向量都位于输入向量聚类的中心。样本的密度分布或者蕴含在输入空间样本背后的其它特征被简单压缩到一个含有有限个节点的竞争平面上，使某些样本在输出空间中相对集中地聚在一起，由此便形成了聚类。

典型SOM网络结构如图1所示，由输入层和竞争层组成。输入层神经个数为m，竞争层由a×b个神经元组成的二维平面阵列，输入层与竞争层各神经元之间实现全连接。

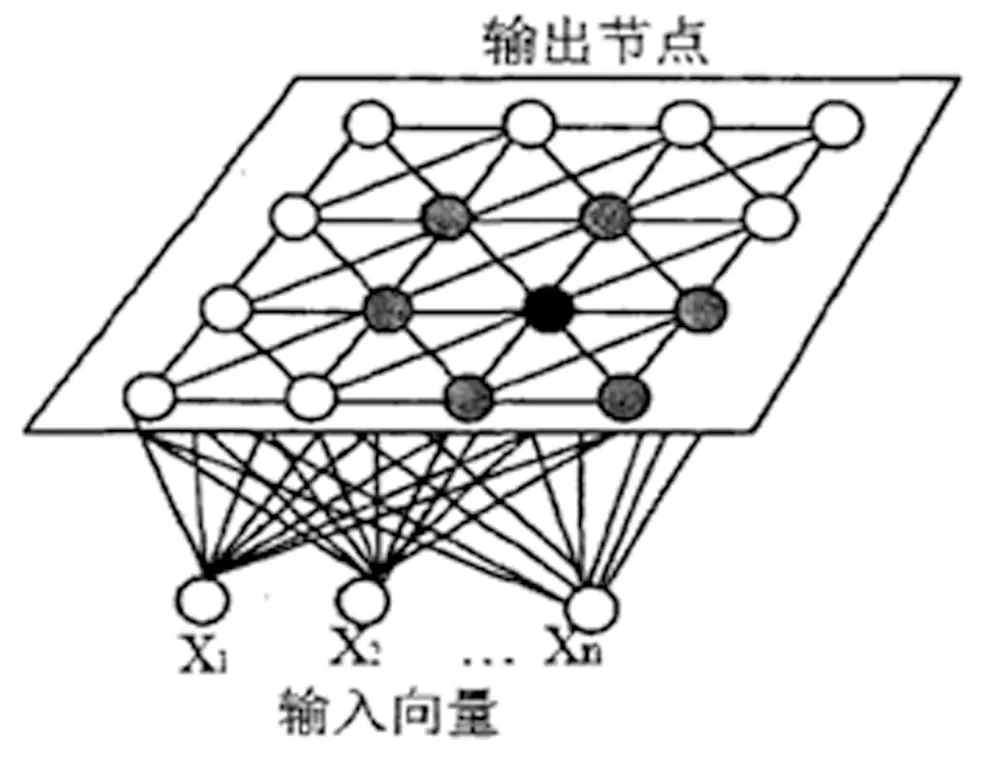
图1 SOM网络结构图

SOM网络的一个典型特征就是可以在一维或者二维的处理单元阵列上，形成输入信号的特征拓扑分布，因此SOM网络具有抽取输入信号模式特征的能力。SOM网络一般只包含有一维阵列和二维阵列，但也可以推广到多维处理单元阵列中去。其算法主要包括以下四个过程[7]：

(1)评估过程

对于每一种输入模式，在对网络中所有竞争节点进行初始化权重之后，计算它们相对于判别函数各自的函数值，其判别函数表达式如式(1)所示：

(1)

式(1)中，xi和wk分别表示输入向量和及其对应神经元的权值。

(2)竞争模式

按照公式(1)所示，对在竞争层拥有最大判别函数值的神经元，可以认定其为本轮竞争的优胜者。其中，可以用欧式距离最小来表示这种特定的输入模式，其函数表达式用公式(2)表示：

(2)

(3)自学习过程

这里使用高斯邻域函数：

(3)

(4)

在批量学习方式下，以优胜神经元为核心的拓扑邻域神经元可表示为：

(5)

(4)自组织过程

在自组织过程中，网络中各个神经元的权值按下面的等式更新。其中，在在线学习方式下，其更新等式为：

(6)

式(6)中为学习效率，在批量学习方式下，其更新等式为：

(7)

1.1.2 RBF神经网络

1988年Brookhead和Lowe将径向基函数(Radical Basis Function，RBF)引入神经网络，RBF神经网络是一种采用局部响应的人工神经网络。其基本理念是通过隐含层对输入层的变换，将低维的输入数据变换到高维模式，将非线性问题转化为线性问题。RBF神经网络属于前向网络，包括输入层、隐含层和输出层，网络结构如图2所示。

图2 RBF径向基神经网络结构

建立一个RBF神经网络的步骤：

(1)建立神经网络，添加所需的训练输入矢量，输入对应的目标矢量以及扩展参数。

(2)按照参数确定的算法进行网络训练，当达到给定误差要求时，确定最终网络各层的权值和阈值，进而确定网络结构用以完成训练。

1.2 SOM-RBF混合算法的预测原理

用电量预测是一个高度非线性问题，大多数预测方法是通过对观察某些特征因子来挖掘背后的信息。然而，这些预测因子的信息之间可能存在着非常复杂的相互作用，因此，在训练时，传统人工神经网络容易出现过拟合现象，这样预测可能会不够准确，但是在这种有特征因子的样本数据中，会有相似的规律可寻，根据输入样本点较相似、密度大时，有领域预测精度更高的网络特性。

实际预测中，组合人工神经网络是一种提高预测精度的有效方法，混合算法是通过对输入样本先聚类，组合成为相似样本，对该样本建立RBF神经网络预测模型，通过对样本分类建模，将原来分布不均匀的各样本点集中到各自相邻的领域，从而预测精度将会大大提高[8]。

图3 SOM-RBF神经网络预测系统工作流程

如图3所示，组合人工神经网络预测的实现步骤如下：

(1)对给定的样本进行归一化处理，其自变量区域为[0,1]，其公式为：

xk=(xk-xmin)/(xmax-xmin)

(8)

公式(8)中，xmin为原始数据的最小值；xmax为原始数据的最大值；

(2)对于归一化后的数据进行SOM聚类分析，调用Matlab中的SOM 神经网络工具箱的函数命令：net=newsom(minmax(p)，[x]);

(3)在SOM神经网络分出的每一种样本类内各自构建一个RBF神经网络，并分别用各种样本类内的训练样本来训练该类的RBF神经网络;

(4)对预测完后的值反归一化处理，得到用电量具体值，通过与实际用电量误差分析，判断该组合神经网络的预测效果。

2 年用电量实际案例仿真及分析

2.1 样本数据选取

本文利用文献[9]给出的从1997年到2016年10个影响因素和湖北省年用电量统计数据(见表1)可以看出，影响用电量的因素有很多种，这说明对用电量的预测是一个高度非线性问题，对10个主要影响因素和湖北省用电量均经归一化处理，作为输入和目标向量。其中，本文采取按数量随机抽取训练样本和测试样本的选取策略，从20个样本选取6、11、15、19、20进行预测解决前组作为网络的训练样本，其余15组数据作为训练样本。由于样本数据向量中各个指标有所不同，为了防止部分神经元达到过饱和状态以及方便计算，先对样本的输入数据进行预处理。

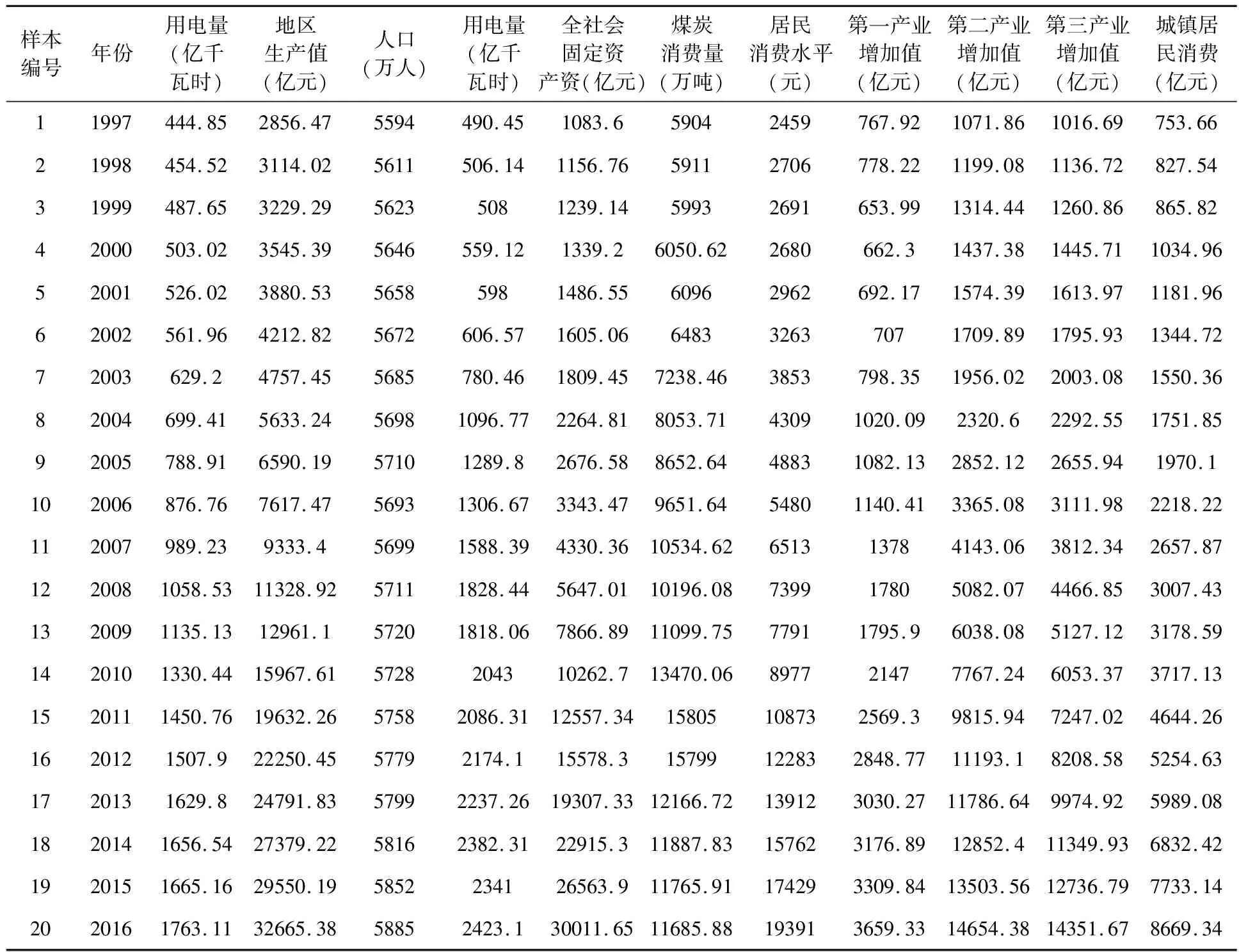
表1 湖北省用电量与影响因素统计表

2.2 用电量预测步骤

(1)本文调用Matlab[10]神经网络工具箱中的函数命令对样本进行分类：

net=newsom(minmax(P)，[1，a])；net.trainParam.epochs=b;

其中，a为分类数目，b为训练次数。由训练结果可知，当训练次数大于200次的时候，训练结果和100次相同，所以，训练次数的增加就没有太大意义。所以选择训练200次。分别取a=3，4，5，如表2所示：

表2 SOM聚类分成三类结果

如表2所示。由实际情况分析和上面三个表格的分类比较可以看出，将20组数据自适应分成4类比较合适。其中预测样本编号6为Ⅰ类，11为Ⅱ类，15为Ⅲ类，19、20为Ⅳ类。

(2)分别针对已经分好的每一类样本采用RBF神经网络进行建模。根据影响用电量的影响因素、实际数据和其网络自身的特点，确定RBF神经网络结构参数，调用RBF网络工具箱如下：

net=newrbe(P，T，SPREAD)

其中 P代表训练样本输入，T代表训练样本的输出，即目标向量，SPREAD为径向基函数的分布密度，取不同的spread值，分别对神经网络进行多次尝试性训练后，Ⅰ类、Ⅱ类、Ⅳ类选取最佳值30，Ⅲ类选取最佳值为0.5。

(3)样本训练过程就是RBF神经网络的建立过程。训练完之后，即可用于对测试样本的预测。

2.3 仿真结果分析

根据上述预测步骤，通过Matlab结合表1数据建立年用电量预测模型进行仿真试验，样本编号6、11、15、19、20作为测试样本，输入到SOM-RBF神经网络预测模型，可以得到该组训练样本下实际值和预测值的对比，如图4所示。

由图4可知，该预测模型在5个样本的预测上有着较好的拟合结果，对相关10个影响因素的变化有着良好的跟踪能力，预测效果较好，并且对年用电量拟合精度较高，有着较为不错的预测表现。

如图5所示，本文分别建立单一的BP神经网络和RBF神经网络，对比SOM-RBF神经网络，可以看出在预测效果上更接近实际值，混合算法比传统神经网络的预测优势更加明显，BP、RBF在19和20样本数据表现出较大的误差，离散程度更大。

图4 年用电量真实值与预测值对比图

图5 三种神经网络对比图

将本文采用的 SOM-RBF 组合网络预测的结果，与直接应用BP神经网络模型和RBF神经网络模型的预测结果进行对比，结果见表3。可以看出，BP网络的预测结果，其相对误差最大达到了16.19%，最小也为2.24%；RBF相对误差最大为9.09%，而混合SOM-RBF 网络组合模型的预测结果，除19号样本外，相对误差都在3%以下。这是因为神经网络预测的准确性和训练样本数据的多少有较大的关系，特别是对BP神经网络来说，如果缺乏足够多的训练数据，网络预测值可能存在较大的误差。而精确网络适合样本数据较少的情况，能够更有效提高误差精度。

表3 三种预测模型预测效果对比分析

3 结论

通过本文对湖北省近20年用电量数据样本进行分析，可以看出用电量是一种非线性数据，传统神经网络在面对非线性问题上有很好的处理能力，这往往需要大量样本进行网络训练，对于预测精度问题仍是研究的重点和难点。在面对用电量数据监测和采集不足的情况下，利用某些影响因素之间的关联性，结合SOM和RBF各自的特点，聚类后再分别建模预测，从而提升预测模型的精度。试验结果表明：较传统BP神经网络和RBF神经网络模型，该方法有更高的拟合精度和泛化能力，预测的相对误差较小，能更加有效地应用到用电量预测中。