基于全局代表指标的LSSVM最优稀疏化算法
张世荣 童 博
(武汉大学 电气与自动化学院,武汉430072)
目前,人工智能(artificial intelligence,AI)已成为全球一大研究热点,正为社会发展带来更多可能性.机器学习作为人工智能的关键环节,也因统计学的坚实基础而获得了迅速发展,众多机器学习算法正被广泛应用于各种各样的场景.最小二乘支持向量机(least square support vector machine,LSSVM)是一种典型的机器学习算法[1].不同于支持向量机(support vector machine,SVM)[2],LSSVM将SVM中的不等式约束转换为等式约束,一方面使得建模过程的计算大大简化;另一方面,等式约束导致其缺失了SVM与生俱来的稀疏性.稀疏化对于LSSVM有着重要的意义,是LSSVM 算法研究的一个重要分支.自LSSVM算法发表以来,对于LSSVM稀疏化的研究便从未停止,涌现了一些可行的稀疏化方法[3-10],大部分算法均源于模型样本剪枝的基本理念.文献[5]也采用样本剪枝思想,但将LSSVM的稀疏化转化为最优化问题来进行求解.其优化问题以样本支持值的绝对值|αk|为指标,以样本剪切率为优化变量对训练样本进行剪切,以获得最小泛化误差.文献[10]定义了LSSVM 训练样本空间中的全局代表指标(global representative indicator,GRI),并以GRI为指标对LSSVM 模型进行了稀疏化,用试算结果证明了GRI指标的有效性.文献[10]中采用的GRI完全不同于大多数LSSVM剪枝稀化算法所采用的|αk|指标,为LSSVM模型稀疏化提供了另外一条可行路径.
本文将对GRI进行完善与发展,并基于GRI建立LSSVM最优稀疏化问题,寻求LSSVM模型稀疏化的一套科学方法.本文的稀疏化算法以校验误差最小化为优化目标,以GRI为指标择选LSSVM的最优支持向量集.鉴于此优化问题的复杂性,无法采用线性规划、二次规划等常规方法进行优化求解.利用粒子群优化算法(particle swarm optimization,PSO)来求解此LSSVM模型的最优稀疏化问题,并针对一个典型的函数模型给出最优稀疏化结果,验证本文提出的最优稀疏化算法的有效性.
1 样本GRI指标
LSSVM模型稀疏化的实质是从原始训练样本集中挑选合适的样本构成样本数更少的训练样本集,并满足某一(或某些)预定指标.可见,样本的挑选依据是模型稀疏化的关键.以往LSSVM剪枝稀疏化算法中,大多数以|αk|为指标,认为具有较大|αk|的样本具有更大的权重,更应该保留到训练样本集.剪枝稀疏化采用迭代方法,在每次迭代中删除具有较小|αk|的训练样本,此类方法在工程中获得了广泛应用,由于评价指标的非单调性,使得剪枝算法难以获得最佳的训练样本集[5].本文采用GRI指标来对训练样本进行择选,GRI是一个混合指标,由样本密度和离散度综合而成.
1.1 密度
在特征空间中,两个样本之间的距离表示为
式中:K(xi,xj)为核函数,采用与LSSVM模型中相同的函数形式.特征空间中任一数据点xi的密度可以用数据点特定邻域内点的个数来衡量;直观而言,样本密度代表邻域内其它样本的聚集程度.定义样本密度为ρ(xi),领域大小为θ,则密度可表达为
其中,n为样本个数,且
可见,样本密度为邻域θ 内样本点的个数,是描述样本聚合度的一种指标,体现了样本空间的局部性特征.
1.2 离散度
样本集中,离散度ζ(xi)是样本xi的另一个指标,定义为该点到比该点密度更大的其他点的最小距离:
式中:X为全体可用样本的集合;D为样本之间距离值的集合.样本离散度也是基于样本距离来定义.计算某一样本xi的离散度时,先将所有密度比xi密度大的样本取出来计算,构成一个距离值集合,再取该集合中的最小值,即各样本与xi的最小距离,作为xi的离散度.但该定义中存在一个例外,若xi是样本集中密度最大的样本,则将其离散度置为样本集中样本的最大离散度,如式(4)所示.
1.3 GRI
从密度和离散度的定义可以看出样本密度具有局部性特征,而离散度具有全局性特征.将高密度点作为LSSVM支持向量可以使得类中心超平面的定位更具有精确性;但是,若仅考虑样本密度,LSSVM支持向量将集中在某个高密度区域,使得训练样本集丧失全局性.在LSSVM样本稀疏化中需要综合考虑局部性和全局性.以下所采用的样本全局代表指标GRI就是一种基于密度和离散度的综合指标,采用以下乘积方案实现指标综合
式中:λ(xi)表示样本xi的GRI.由于式(5)中ρ(xi)和ζ(xi)在数值上可能有不同的数量级,在进行乘积综合处理前需要对密度和离散度分别进行归一化.显然,GRI是综合考虑样本局部代表性与全局代表性的综合指标,GRI值更大的样本能更好地代表整个样本集,应该被选作LSSVM模型的支持向量.
1.4 邻域
样本密度定义中,邻域θ 是一个敏感参数,直接影响着样本密度和离散度.图1为2维样本的示意图,可见θ越大则密度ρ越大,样本代表性指标GRI作用距离越大,样本影响范围也就越大.GRI的大小将直接改变LSSVM 训练样本的选取结果,影响稀疏化性能.在本文后续最优稀疏化问题中,邻域θ 也将作为优化变量之一,通过最优化算法获得θ 的合适取值.
2 基于GRI的LSSVM 最优优化稀疏化
2.1 优化问题
根据LSSVM理论,LSSVM回归可以表达为
式中:y(x)为LSSVM回归输出;xk(k=1,2,…,N)为支持向量;αk为支持向量的支持值;N为支持向量个数.LSSVM稀疏化即从原始训练样本集中挑选合适的N个样本构成模型的支持向量集.以下将LSSVM稀疏化转化为最优化问题进行求解.
设有L+M 个可用训练样本,样本归一化后被分成两组:第一组样本集XL包含L个样本,XL=,用于模型训练;第二组样本集XM包含M 个样本,,用于模型校验.稀疏化问题以校验样本输出与模型预测输出的均方根误差(root-mean-square error,RMSE)为评价指标,RMSE计算如下:
其中,yj为第j 个校验样本的输出.
设φ为LSSVM模型的样本剪切率,θ为邻域,将它们记作参数向量ε=[φ,θ].基于GRI的LSSVM稀疏化问题计算过程如下:先确定邻域θ,计算样本集XL中每个样本的密度ρ和离散度ζ,综合ρ和ζ 获得样本的GRI指标,再按照GRI降序排列,获得排序后的GRI向量如下:
确定φ,从XL中去除排序末尾φ%的样本,将剩余N 个样本作为LSSVM的训练样本 集XN[φ,θ],训练样本个数记为:
式(11)中:
取校验样本输出与模型预测输出的均方根误差为目标函数,取参数变量ε=[φ,θ]为优化变量,则LSSVM的稀疏化过程可以转换为如下最优化问题:
2.2基于PSO 的优化求解
在最优化问题(15)的求解中包含样本的GRI排序等操作;优化变量ε=[φ,θ]与优化目标RMSE 之间为非线性关系,且没有确定的数学表达式.因此,线性规划或二次规划等经典算法无法求解此类优化问题.遗传算法(genetic algorithm,GA)、PSO等智能算法可以作为以上优化问题的解决方案.其中,PSO因计算过程简单,收敛迅速以及可调参数少等优点,在诸如机械、化学、民事、航空航天等众多领域获得了广泛应用,PSO 也将用于求解本文提出的优化问题.
在使用PSO 算法之前,需要确定适应函数.本文将优化问题(15)的目标函数作为PSO 算法的适应函数.适应函数具体为:
基于PSO 的LSSVM最优稀疏化问题的求解流程如图2所示.
确定适应函数及粒子群规模p之后,结合训练样本集XL和校验样本集XM,算法进入第一次迭代.首先,初始化全部p个粒子的位置Q1=(Q11,Q21,…,Qp1)和速度V1=(V11,V21,…,Vp1);其中,Qi1=εi1=[φi1,θi1]表示第一次迭代内第i 个粒子的位置,Vi1=[Δφi1,Δθi1]为第一次迭代内第i 个粒子的速度.初始化完成后,对于每一个粒子,算法根据粒子的θ 值计算训练样本集XL中全部样本的GRI并将样本按GRI降序排序,获得排序后样本集.排序完成后,算法根据粒子的φ值,剪切去除样本集末尾φ%的 样 本,获 得 支持向量集并用训练LSSVM模型.然后,以校 验样本集XM中的xj,(j=1,2,…,M)为LSSVM模型输入,计算模型预测值y[φ,θ](xj),结合样本校验值yj,(j=1,2,…,M),计算该粒子的适应函数值RMSE.依次计算所有粒子的适应函数值,并记录粒子的个体最优适应函数值i_best及其对应位置Qi_best;记录并导出所有粒子的全局最优适应函数值g_best及其对应位置Qg_best.一次迭代完成后,所有粒子都需要更新位置,更新算法如下:
式中:Vik、Qik分别表示第i 个粒子在第k个搜索周期中的 速度和 位置;ω为PSO 算法的惯性权重;c1、c2为算法的两个学习因子;r1和r2为[0,1]区间内的随机数.所有粒子更新位置后,进入下一次迭代,直到满足搜索结束条件,PSO 结束搜索,输出最终结果.
3 算法验证
3.1 函数模型
为了验证以上提出的基于GRI的LSSVM最优稀疏化算法,并便于直观展示算法结果,选取二维sin c函数进行验证,该函数表示为:
当输入向量x=[x1,x2]T,在x1∈[-10,0)∪(0,10]且x2∈[-10,0)∪(0,10]范围内取值时,函数的曲面如图3所示.
sin c函数曲面存在较大的波动,规律复杂,是例证支持向量机回归模型的合适对象,在文献中也获得了广泛认同.为了使得样本更加贴近工业实际,在sin c函数值上刻意引入干扰以仿真测量误差:
其中,μ为随机数且μ∈[0.015,0.02].
3.2 算法结果
首先,对样本进行归一化处理;然后,根据式(1)计算样本集XL中样本点两两之间的距离值,距离值都处于区间γ=[0.058 9,1.414 2]内.故在以下计算中将邻域值θ的取值范围限定于区间γ内以缩小PSO 的搜索空间,加快求解速度.在优化问题的求解计算中,LSSVM核函数设置为径向基核函数(RBF),正规化参数c=50,核参数σ2=10,PSO 粒子群规模设置为p=40,惯性权重ω=0.9,两个学习因子c1=2,c2=2,粒子最大速度为搜索范围的30%.PSO 的结束条件设置为:当适应度函数全局最优值g_best在连续250次迭代中未变化时,停止PSO搜索过程.所有计算于Matlab 2016b平台进行,软件运行于一台个人电脑,该电脑搭载频率为2.30 GHz的Core i5-8300 H CPU.
PSO 迭代过程中,适应函数全局最优值g_best的变化趋势如图5所示.可见,PSO 在约190次迭代后即取得了适应度函数的最小值0.060 7;此时,PSO粒子聚拢到点[φ*=0.556 6,θ*=1.328 29],该点即为LSSVM 模型稀疏化问题的最优解.即,当邻域θ取1.32829且将按GRI降序排序后,切除样本集XL末尾55个样本,保留前45个样本作为支持向量时,LSSVM 模型具有最佳性能,可以获得最小的RMSE.
为了验证基于GRI指标择选LSSVM支持向量的有效性,将XL的100个训练样本呈现于图6.图6中“+”为训练样本,“⊕”为经过PSO优化后选作支持向量的45个样本.图6(a)横轴为密度纵轴为离散度;图6(b)增加了GRI维度,将训练样本呈现在三维坐标.从图6中可见,支持向量都具有较大密度或离散度,进而具有较大的GRI综合指标.当LSSVM 模型选用此类样本为支持向量时,模型在校验样本集上取得了最小RMSE.以上结果验证了以GRI为指标择选LSSVM模型支持向量的有效性,且证明了GRI指标与样本重要程度之间存在确定的正相关关系.另外,图6还表明,本文采用最优化获得了支持向量的最佳数量,为LSSVM模型的稀疏化建立了一种更加科学的方法.
再将支持向量呈现于sin c函数的自变量空间.如图7所示,图中“+”为训练样本,“⊕”为经过优化获得的45个支持向量.从图7 中可以看出LSSVM模型的支持向量在sin c函数的二维平面上分布均匀,从直观上看这些支持向量具有更好的全局代表性.在LSSVM剪枝稀化算法中一般以样本支持值的绝对值|αk|为指标,而本文采用GRI为指标.
为了对比二者的关系,将以上支持向量的GRI值和支持值α 陈列于图8、表1进行比对.由图8、表1可见样本的GRI指标与支持值α并无明显相关性,GRI指标是一个完全独立于样本支持值的样本属性.
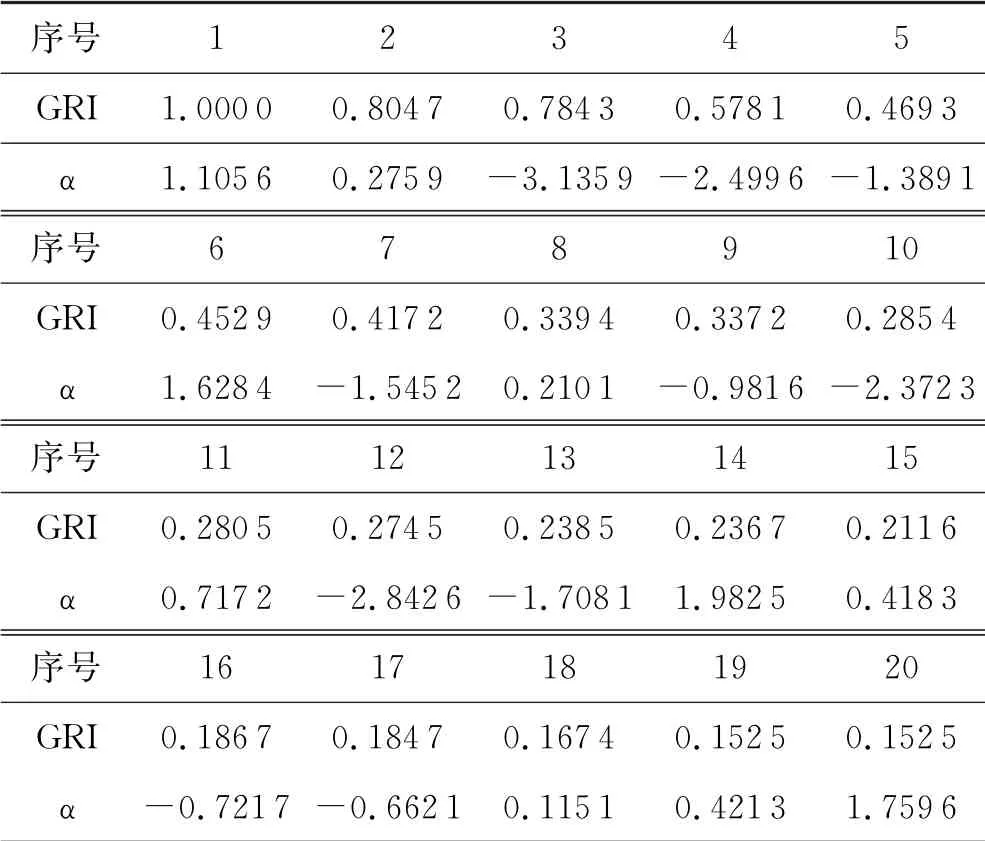
表1 GRI与支持值
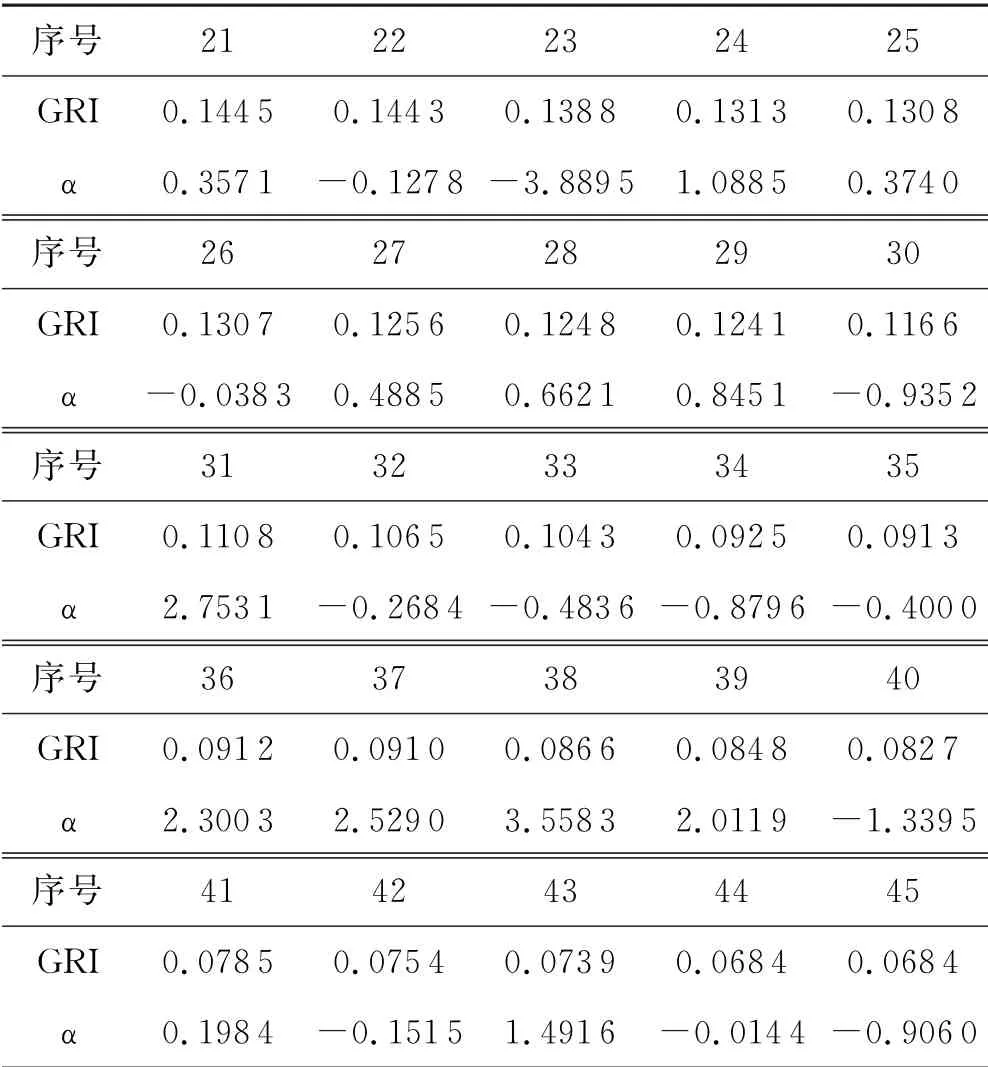
续表1 GRI与支持值
为进一步验证采用本文所提稀疏化方法LSSVM模型的泛化能力,本文引用了另外两种LSSVM稀疏化方法进行对比研究.一种为Suykens提出的经典稀疏化方法[3],为了便于叙述,将基于经典方法稀疏化处理的模型记为LSSVMclassical.另外一种为文献[5]提出的基于支持值和PSO 优化的稀疏化方法,以下将经该方法处理的模型记为LSSVMα+PSO.将本文稀疏化方法处理后的模型记为LSSVMGRI+PSO;另外,还将未经处理的原始训练样本也加入对比,其模型记为LSSVMorignal.
仍取图4所示训练样本和校验样本为范例开展以下对比研究,并另外均匀选取100个样本构成测试样本集XE,用于测试各模型的泛化能力.所有稀疏化方法从样本集XL选训练样本,用样本集XM做校验,用样本集XE验证泛化能力.
首先,用100个原始训练样本XL对模型进行训练,获得LSSVMorignal模型.再以测试样本集XE验证LSSVMorignal模型,计算LSSVMorignal模型在XE上的RMSE,见表2;并将测试样本的真实值和预测值绘制对比曲线,如图9(a)所示.然后,用经典稀疏化方法对训练样本集XL进行稀疏化处理.该稀疏化过程采用迭代形式完成,并以样本支持值绝对值|αk|为指标对训练样本进行剪切.当迭代过程的RMSE 指标劣化时,LSSVM的稀疏化过程结束.最终,经典稀疏化方法保留了80个样本作为LSSVMclassical模型的支持向量.以测试样本集XE验证LSSVMclassical模型,获得测试样本集的RMSE,如表2所示.将XE的样本输出与LSSVMclassical模型预测输出进行对比,结果如图9(b)所示.
重复以上过程,分别以文献[10]所提的稀疏化方法以及本文所提的最优稀疏化方法对XL进行模型稀疏化,分别获得LSSVMα+PSO模型和LSSVMGRI+PSO模型.此两个LSSVM模型的测试指标和比对曲线分别如表2、图9(c)和图9(d)所示.

表2训练样本集对比
从对比表2中可以看出,LSSVMGRI+PSO模型具有最大的样本剪切率,最小的样本容量,仅保留45个样本作为模型支持向量;且在测试样本集上的RMSE最小0.061 3.本文提出的基于GRI指标的LSSVM稀疏化方法,由于采用了最优化方法,可以实现稀疏化性能和校验误差性能的双重优化.LSSVMα+PSO模型也采用了最优化方法,该模型采用|αk|为指标,而αk必须在LSSVM训练后才能获得;与之相比GRI指标直接源于训练样本集,无需LSSVM 训练.每次优化迭代GRI+PSO 稀疏化方法比α+PSO方法少一次LSSVM模型训练,这可以大大简化模型的计算过程.经典稀疏化方法在每次迭代中都会判别性能指标是否劣化,并把它作为是否结束稀疏化的判据.若RMSE指标呈现非单调特性,则此方法就无法获得较好的稀疏化结果,这一点在表2中获得了验证.
图9的对比曲线中,红色实线代表LSSVM模型的预测输出值,蓝色虚线代表校验样本集XE的真实值.可以看出,与其余3 个模型相比,LSSVMGRI+PSO模型的预测输出对测试样本的跟随效果更佳,体现出较好的泛化性能.
4 结论
稀疏化是最小二乘支持向量机研究的重要环节,对其算法的研究具有重要意义.本文在样本全局代表点的基础上进行了完善,提出全局代表指标GRI.基于GRI进一步提出了一种LSSVM最优稀疏化算法.算法以样本剪切率和邻域大小为优化变量,以RMSE 为优化目标,将稀疏化问题作为优化问题求解,获得了一种更加科学的LSSVM模型稀疏化方法.针对优化问题的复杂性提出了基于PSO的求解方法.取二维sin c函数为对象对算法进行了验证,并对3种方法进行了对比研究.结果揭示了GRI与样本重要程度之间的正相关关系,且表明GRI与支持值α并无明显相关性,是一个完全独立于样本支持值的样本属性.本文提出的基于GRI的LSSVM稀疏化算法采用最优方法在3种方法对比中取得了最佳性能,能同时获得最大的样本剪切率和最小的RMSE指标.本文的最优稀疏化算法实现简单,适合LSSVM模型的在线应用.

