反馈控制对工期不确定的并行耦合任务完工时间的调节

田启华 李 浪 杜义贤 周祥曼 鄢君哲

(三峡大学 机械与动力学院,湖北 宜昌443002)

复杂产品由于设计环节较多,不同阶段设计任务之间频繁的信息交流会导致大量的迭代返工,这使得产品设计任务执行时间难以预估[1].实际产品开发过程中存在着如市场需求的变化、关键技术无法攻克、任务执行工期和资源分配不均等不确定性因素,它们同样会增大产品开发完工时间的不确定性.为了更客观地反映耦合设计任务的不确定执行工期和减小这种不确定性对产品开发完工时间的影响,必须采用一种自适应机制来加以调控.针对该问题,国内外许多学者展开了广泛研究.如:金宏,王宏安,傅勇,等[2]提出一种基于模糊反馈控制的调度算法将任务集按不同的优先等级进行划分,控制了任务的截止期错失率；虞忠伟,陈辉堂,王月娟[3]针对具有不确定项的重复非线性时变系统,提出了基于反馈控制的迭代学习控制器来调整系统的最终跟踪误差界；俞岭,谢奕,陈碧欢,等[4]提出了一种基于控制理论的虚拟资源动态分配方法,从而实现应用系统的优化运行和虚拟资源的有效利用；Kim[5]将离散状态空间模型用于耦合迭代中工作转移矩阵的表达,通过离散状态量来预测耦合迭代过程的动态特性；Ong等[6]提出一种齐次状态空间表示法,对整个并行设计迭代过程进行建模和监控；Huang H Z 等[7]将产品开发过程看作带反馈信息的动态系统,并结合设计结构矩阵获取任务间的交互信息；邓腾,戴紫彬,张立朝,等[8]针对不确定条件下任务完工错过率过高以及调度过程稳定性差的问题,运用反馈控制机制将各任务的错过率偏差反馈到控制器,然后根据偏差值对任务的执行优先级进行调整；陈振东,郑应平[9]针对传统的任务调度过程要求给出一定的资源裕度来保证各任务不会因资源受限而发生延迟执行,提出了运用反馈控制的方法提高任务执行过程资源的利用率；吴卫东,黄洪钟,古莹奎[10]通过对多目标优化问题不确定性因素的分析,将协调校正权函数、优属度函数和重要性加权因子引入闭环反馈控制中,从而得到了多目标满意解的优选方法.上述文献从不同角度阐述了反馈控制机制对所研究目标或对象的调控作用,但是这些方法很少有针对任务工期不确定条件下的并行耦合设计迭代过程的研究.

本文针对产品开发过程中任务工期的不确定性,利用工期的区间数描述方式构建了工期不确定条件下的并行耦合迭代时间模型,并结合迭代收敛条件和工期满意度区间条件得到了并行耦合迭代反馈控制模型.该模型通过调整任务的返工量来加快任务迭代速率,从而减小任务工期不确定性对并行耦合迭代完工时间的影响.

1 任务工期不确定的并行耦合迭代时间模型的构建

在确定性环境下,耦合任务集的工期矩阵W 可以表示为:

式中:W 为对角矩阵,其元素wi表示每个任务确定的工期值,N为任务的个数.

实际产品开发中,任务之间频繁的信息交互导致的迭代返工使任务的执行工期具有不确定性.为了更客观地反映这种不确定性,采用区间数[11]来描述任务的工期.定义此时的工期矩阵为:

式中:[wvi]为用区间数表示的任务工期.

并行耦合迭代模型中的工作转移矩阵WTM包括两部分的数值信息,即任务返工量数值矩阵RA和任务工期数值矩阵W[12].并行耦合任务迭代过程中可用向量u(t)来描述第t次迭代时任务的工作量,假设任务的返工量不随时间而变化,依据线性规则有:

根据并行耦合迭代方式的特点可知,完成整个迭代过程所消耗的时间为每个迭代阶段所消耗时间之和,而每个迭代阶段所消耗的时间由该阶段中迭代时间最长的任务决定,即[13]:

式中:t为当前迭代次数,M 为迭代终止次数,[·](i)表示向量的第i个元素,u0为全1的工作量向量.

将式(2)代入式(4)中可以得到工期不确定条件下并行耦合任务迭代时间模型:

2 区间数的运算和比较

求解工期不确定条件下并行耦合任务迭代时间模型涉及到区间数的运算和比较.

设Q={[aiL,aiR]}(1≤i≤m)是一组包含了m个区间的集合,则区间数运算规则[14]如下:

式中:c 为常数；aiL和aiR分别表示区间ai的左右端点.

为了比较多个区间数的大小,通常采用可能度计算的排序方法对各个区间进行排序[15].设有区间数a=[aL,aR]和b=[bL,bR],定义P(a≥b)为a≥b的可能度,可能度计算式为:

式中:L(a)=aR-aL,L(b)=bR-bL可能度的6种取值代表了任意两个实数区间在数轴上6种可能的位置关系.

可能度的取值在0～1之间,可以用它来衡量相互比较的区间数之间的大小关系；假设有m个区间数,它们之间进行两两比较,其结果可以组成一个m阶的可能度方阵P=(pij)m×m；建立可能度方阵后,就可以对m个区间数排序.文献[16]给出了可能度方阵的排序公式:

通过式(9)得到排序向量ω=(ω1,ω2,…,ωm)T,按其分量的大小对各区间进行排序,得到各区间的大小关系.

3 反馈控制调节过程分析

在产品开发中通常希望其完工时间能够在预期的时间区间内波动,任务工期的不确定性将增加项目完工时间的不确定性；为了降低这种不确定性的影响,引入反馈控制方法实现迭代过程的自适应调节.反馈控制流程图如图1所示.

图1中Wv为输入的不确定性工期矩阵,u0是任务初始工作向量,RA是耦合任务集的返工量矩阵；时间累加器用于累加耦合任务集每次迭代的时间,T为其输出量；Tv表示为满足满意度要求的耦合迭代完工时间区间；K表示反馈调节矩阵,该矩阵的元素kij代表为了使整个耦合迭代过程达到期望的结果而额外分配给每个任务的资源量.即,基于反馈控制的并行耦合任务的返工迭代模型可表示为:

式中:RA(t+1)为第t+1次迭代时由发生返工的任务组成的返工量矩阵,为了简化模型,这里假设RA是一个不随时间变化的矩阵.从式(10)可知,反馈调节矩阵K通过调整任务的返工量,使整个并行耦合迭代的完工时间向满意度区间靠拢,从而减小完工时间的不确定性.

根据第2节所提工作转移矩阵的意义和项目管理者的实际工程经验,确定与迭代过程相对应的返工量矩阵RA以及任务不确定性工期矩阵Wv,并进一步确定并行耦合迭代过程的收敛阈值ε 和完工时间的满意度区间Tα.反馈调节过程应满足以下不等式:

由式(5)和式(6)求解较大规模耦合任务集时,得到的迭代终止次数M 和反馈调节矩阵K并不唯一,为了求得满足要求的最小反馈调节矩阵K和相应的迭代终止次数M,现作如下分析.

返工量矩阵RA的最大特征值决定了并行耦合任务迭代过程的收敛性,且在增加资源加快设计迭代过程时,耦合任务集的内部迭代属性未发生变化,即每个迭代阶段的关键任务[17]没有改变.此处定义任务模态的概念,任务模态是指以返工量矩阵的特征值与特征向量为标志的耦合任务间相互作用的特性；特征值对应的特征向量定量地表示了各耦合任务在迭代过程中对任务工作总量的影响率.返工量矩阵RA的最大特征值对应的特征向量为耦合迭代过程中的主模态(影响率最大的任务模态),主模态中各任务对应的分量各不相同,这种不同反映了各耦合任务对任务工作总量影响程度的差异.

由于反馈调节矩阵K中的元素kij表示为了使整个耦合迭代过程达到期望的结果而额外分配给每个任务的资源量,这里假设各任务的初始工作量为单位1,kij可以等效于各任务需要进行的额外返工量占初始工作量的比例,即整个反馈调节矩阵K可以等效于1个返工量矩阵,它和返工量矩阵具有相同的属性,可以用来调节返工量矩阵RA的最大特征值对应的主模态.

基于以上分析,可以假设矩阵K和RA具有相同的特征向量,唯一不同的是这两个矩阵的最大特征值不同.根据矩阵论知识可知,当矩阵RA有不同的特征值时,它可以表示为:

式中:V和S分别为矩阵RA的特征值矩阵和特征向量矩阵.

若令矩阵RA的最大特征值为λmax,矩阵K的最大特征值为为矩阵K的特征值矩阵),则有:

式中对角阵diag(λmax-λ*max,…,0)的阶数与耦合迭代的任务数相等；将式(14)代入式(11)和式(12)可求得最小的反馈调节矩阵K和迭代终止次数M.

4 示例分析

以某空气净化器的开发过程为例[18].结合设计结构矩阵DSM,并使用划分、聚类运算得到一个包含风扇设计A、空气过滤器设计B、水箱设计C、智控系统设计D 和主体设计E 5个设计任务的耦合任务集,其耦合信息如图2所示.

图中0至1之间的数字表示对应任务的返工量大小,蓝色格子代表各子任务的工期,TL和TR分别表示对应任务执行工期的区间数左、右边界值.

耦合任务集返工量矩阵:

任务不确定性工期矩阵:

令初始工作向量u0为:

现设定耦合任务集完工时间满意度区间Ta=[36,44],迭代收敛精度ε=5%.当调用反馈控制环节时,根据式(11)和式(12),需满足如下不等式:

矩阵RA的最大特征值；

矩阵RA的特征向量矩阵:

式中:i为虚数单位.

将式(20)和式(21)代入式(14)可以简化式(18)和式(19)的求解过程,从而得到最小的矩阵K和相应的迭代终止次数M.

在给定的任务工期范围内按依次减小区间半宽(区间长度的一半)的方式选取3组任务工期分别代入式(5),利用Matlab计算得到如表1所示的未调用反馈控制的耦合任务集的迭代次数和完工时间；同理将3组任务工期分别代入式(18)和式(19)得到如表2所示的调用反馈控制的耦合任务集的迭代次数和完工时间.

表1未调用反馈控制的耦合任务集迭代结果

由表1可知,在未调用反馈控制的情况下,将原任务工期作为第1组参数输入时,耦合任务集迭代终止次数为10次,完工时间区间为45.6:48.3 d；将第2组任务工期参数输入时,耦合任务集迭代终止次数为8次,完工时间区间为43.5:47.8 d；将第3组任务工期参数输入时,耦合任务集迭代终止次数为7次,完工时间区间为42.2:45.6 d；即3组任务工期对应的耦合任务集完工时间均大于设定的满意度区间.

调用反馈控制的耦合任务集迭代结果见表2.

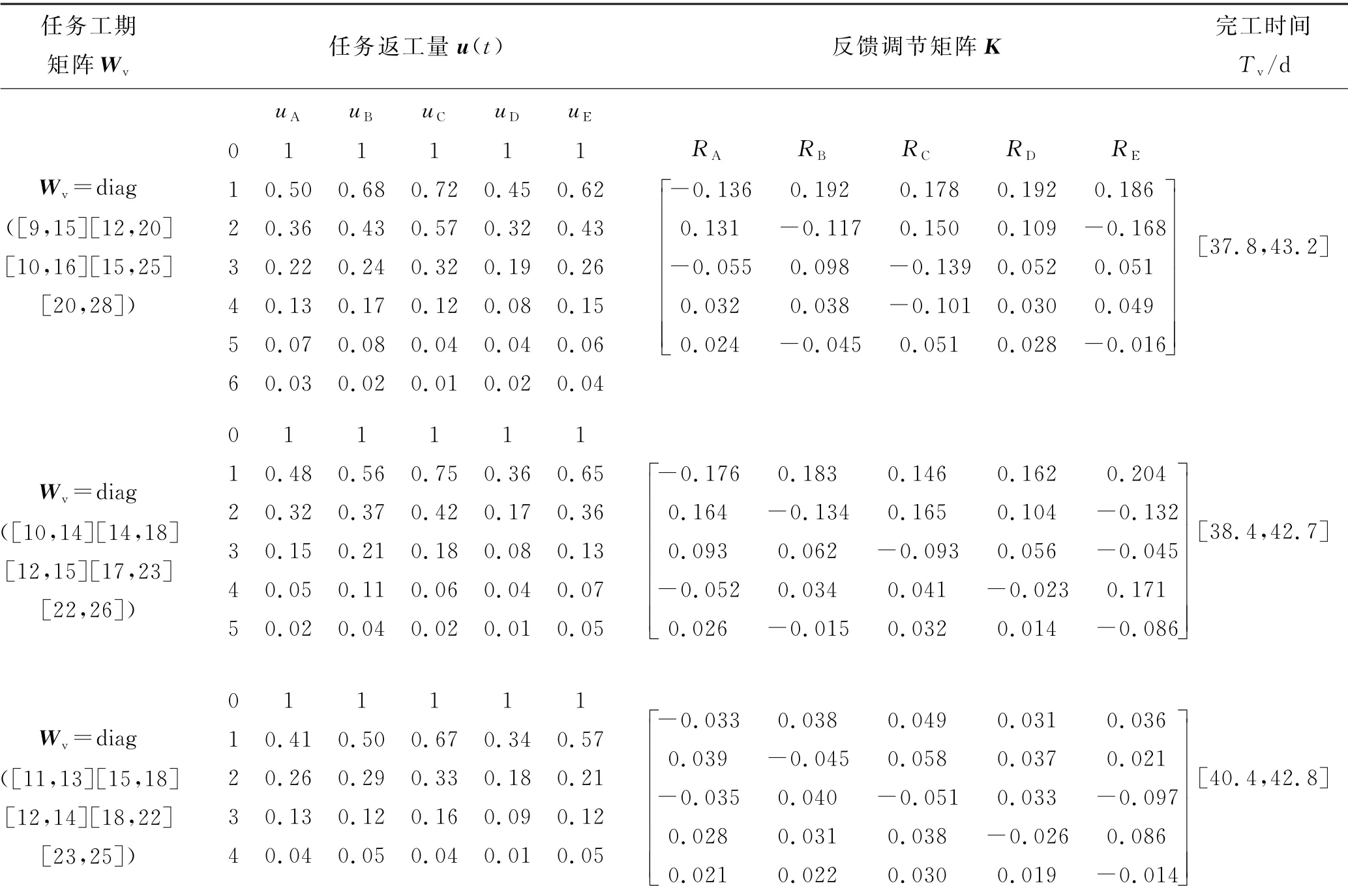
表2调用反馈控制的耦合任务集迭代结果

由表2可知,在调用反馈控制的情况下,将原任务工期作为第1组参数输入时,耦合任务集迭代终止次数为6次,完工时间区间为37.8:43.2 d,反馈调节矩阵K为非零矩阵(单元数值0.131代表当任务A在某一迭代阶段的工作量为100%时,任务B需要分配初始资源的13.1%完成额外的工作量)；将第2组任务工期参数输入时,耦合任务集迭代终止次数为5次,完工时间区间为38.4:42.7 d；将第3组任务工期参数输入时,耦合任务集迭代终止次数为4次,完工时间区间为40.4:42.8 d.

将表1和表2的数据作对比可知,采用反馈控制方法可以有效地减小任务工期不确定性给整个并行耦合任务集的完工时间带来的影响,使项目完工工期的不确定性降低,从而向预期的满意度区间靠拢.

5 结论

产品开发中任务工期的不确定性会增加耦合任务集完工时间的预估难度,运用区间数和区间序可能度对不确定的工期区间进行描述以及大小比较可以更加真实地反映这种不确定性；结合工程中的满意度概念和迭代收敛条件,将反馈控制方法运用于并行耦合任务集的迭代中,可以降低耦合任务集完工时间的不确定性.该方法对实际的产品开发过程具有一定理论指导意义.