基于Copula-RF的混凝土坝变形监测模型

陈诗怡杨 杰程 琳郑东健胡宸瑞

(1.西安理工大学 水利水电学院,西安710048；2.西安理工大学 西北旱区生态水利国家重点实验室,西安710048；3.河海大学 水利水电学院,南京210098；4.福建省电力有限公司 莆田供电公司,福建 莆田351100)

我国是当今世界上拥有水库大坝数量最多的国家,水利工程的安全可靠运行直接关系到人民生命与财产安全,如何保障水库长期安全可靠运行一直是众多学者们的关注重点与研究热点.混凝土坝凭借其安全可靠的性能一直是我国大坝建设的推荐坝型之一,其坝址多位于高山峡谷,常面临人工运行维护困难的问题.同时,混凝土坝运行期外部环境复杂[1],影响因素较多[2],进一步加剧了后期监测、馈控的困难.作为真实、直接、准确反映混凝土坝安全性态的典型物理量之一,大坝变形监测分析常被用于馈控混凝土坝坝体结构运行安全.因此,如何依据混凝土坝变形与环境量监测资料,建立起精准、高效的混凝土坝变形监测模型是大坝安全监控研究的重要问题,也是实现快速反应、准确预测混凝土坝性态演化趋势分析的基础问题.

混凝土坝变形预测的精度通常受到影响因子的选取和建模方法的影响.现有建模方法主要有以下几类:确定性模型、统计模型、组合模型以及混合模型.确定性模型与统计模型最为常用[3],但无法明确大坝材料参数及边界条件,模型无法精确简化；传统统计模型结构简单易于识别,但无法考虑复杂因素的多重线性问题,其预测效果一般[4].近年来,随着大坝安全监控、人工智能等理论的迅速发展,其在处理监控模型因子不确定性及非线性等问题上显现出巨大的优势.如人工神经网络等模型,具有较强的非线性和自学能力[5],但理论体系不完备；而作为一种新的机器学习技术,随机森林(RF)[6]理论体系完备,已在医学[7]、金融学、生物学[8]等领域得到了广泛的应用,其算法特点同样适用于解决混凝土大坝监测数据分析中的非线性和共线性问题.对于影响因子优选方法,常用的混凝土坝变形监测模型影响因子确定方法包括:先验知识法[9]、主成分分析法[10]、灰色关联度分析法[11]等.先验知识法方便计算、效率高但过于依托历史经验,计算结果误差较大；主成分分析法避免了因子相关性影响,但当因子共线性较差时指标计算精度不高,且无法进行回归计算；灰色关联度分析法避免了原始信息不足的缺陷但未明确因子判断准则.因此,在混凝土坝变形预测模型影响因子的选择上存在不完善等问题,随机森林(RF)算法在运算量无明显改善的情况下提高了预测精度,同时对缺少和非平衡的数据比较稳健,能很好的预测多变量.

因此,针对变形监测数据的非线性特点本文提出了一种基于Copula理论和随机森林算法(RF)的混凝土变形预测模型,能够有效地处理、分析和预测混凝土重力坝变形监测,从而实现影响因子集的优选和重要性度量,提高了模型的预测精度及泛化性,更加真实的反应大坝的工作性态.

1 Copula理论

1959年Sklar提出Copula理论[12]；2006年Nelsen进一步完善了其理论体系.Copula理论提出对于任意一个多元联合分布,皆能够进一步细分为一个Copula函数以及其所对应的边缘分布.Copula函数将变量的边缘分布函数和它们的联合分布连接在一起,且不要求边缘分布为同一个函数.

Copula函数的定义是在n维空间[0,1]n的联合分布函数,其边缘分布是[0,1]上的均匀分布,其可表示为:

式中:F(x1,…,xn)为变量xn的联合分布函数；un=F(xn)为变量xn的边缘分布函数；θ为Copula函数参数；C(·)为Copula函数.

1.1 相关性测度

Copula函数中通常采用相关系数描述变量间的相关性,但相关系数仅能够反映变量间的线性相关情况,无法刻画非线性相关性.对此,通过对Copula函数的随机变量做严格的单调增变换,从而使Copula函数能通过相关性测度实现变量非线性相关关系的刻画,常用的相关性测度包括:Kendall秩相关系数、Spearman相关系数ρ 和Gini关联系数γ.由于Kendall秩相关系数和Spearman相关系数ρ 仅能够处理随机变量的变化方向一致问题,而Gini关联系数γ能够衡量随机变量变化方向和变化程度一致性,故本文选择Gini关联系数进行变量非线性相关性度量.

设从二维向量(X,Y)中选取容量为n的样本(x1,y1),(x2,y2),…,(xn,yn),其中X、Y为随机变量.将x1,…,xn按从小到大顺序排列后,xi的名次ri称为它的秩,同样yi在y1,…,yn中的名次(秩)记为si,Gini关联系数γ计算公式如下:

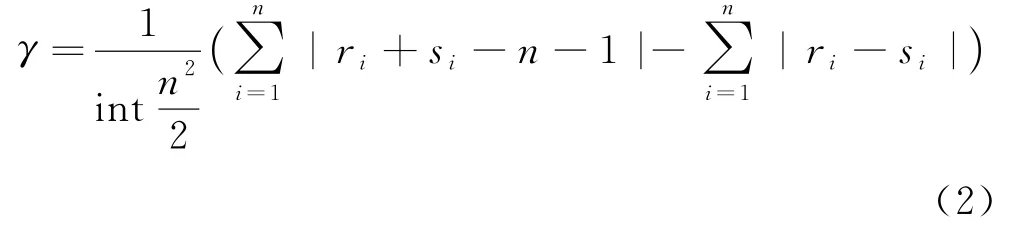
式中:int(·)表示为取整函数.

1.2 Copula函数的选择

常见的Copula 函数分布族分为椭圆分布族Copula函数和阿基米德分布族Copula函数.其中,椭圆分布族具有性质简单、应用广泛的特点,包含正态Copula函数和t-Copula函数；阿基米德分布族,常用的有Gumbel Copula、Clayton Copula和Frank Copula.考虑到t-Copula函数对随机变量间相关关系的变化敏感度强,且能较好地刻画尾部相关关系,因此本研究采用椭圆分布族的t-Copula函数进行计算.

1.3 参数估计

在确定模型中,对于Copula函数模型中未知参数的选择,常采用分布估计、最大似然估计、半参数估计和非参数估计.IMF 估计具有计算量小、便于实现的特点,本文采用IMF估计确定Copula函数模型中未知参数,其基本思想是将Copula函数的参数和边缘分布函数的参数分步进行估算.其实现步骤如下:

1)首先,根据X、Y的边缘分布建立对应的样本(xi,yi)对数似然函数,即

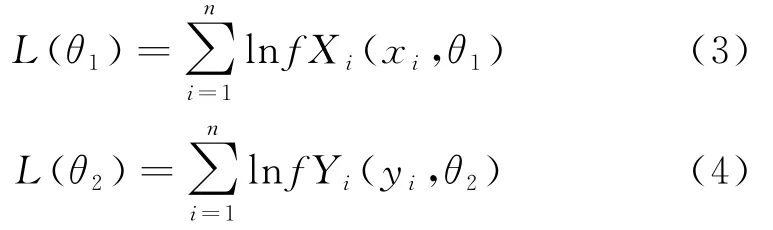
2)利用极大似然估计法求出θ1、θ2的极大似然估计值,即

3)最后求出Copula函数中的未知参数θ 的估计值,即

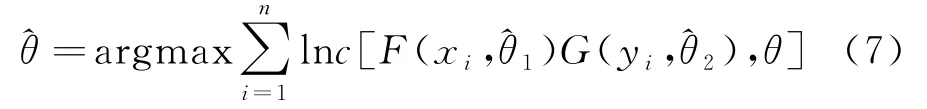
其中,(xi,yi)(i=1,2,…,n)为取自二维向量(X,Y)的一组样本,相应的随机变量X、Y的边缘函数分别为F(x,θ1),G(y,θ2),边缘密度函数分别为f(x,θ1)、g(y,θ2),其中θ1和θ2是两个未知参数,^θ1和^θ2分别是θ1、θ2的极大似然估计值.

2 随机森林原理

随机森林(RF)是由Breiman 和Culter在2001年提出的理论,是根据贝尔实验室所提出的随机决策树方法把分类树组合成随机森林.即从原始数据进行重采样,主要使用boot-strap方法生成多个样本.然后为每个自举样本构建分类树,最终通过集成所有决策树的预测结果,确定投票数最多的为最终预测结果.随机森林通过集成学习的思想,克服了随机决策树过拟合的问题,对缺失数据、不平衡样本和异常值比较稳健,有较高的预测准确率,且运算量没有显著提高,被誉为当前最好的算法之一.

随机森林是由一系列树状分类器{h(x,θk)},k=1,…所构建而成的一个分类器,树状分类器的数量以k 表示,输入样本向量以x表示,θk所表示的是独立同分布的随机向量,即第k棵数的参数向量,一个输入向量x的预测值y为所有树{h(x,θk)},k=1,…的输出结果的平均值.假定对独立分布的X、Y 训练样本集中抽取出,那么随机森林预测值的均方泛化误差计算公式为:

当随机森林中的决策树数量达到一定需求时,随机森林的泛化误差收敛于一个有限值,所以随机森林能有效地避免过拟合,提高了模型对数据的适应性.

综上所述,随机森林算法流程如下:

1)原始数据含有N 个样本,利用boot-strap进行随机抽样,抽取k个训练样本并形成对应的决策树,各样本容量和原始数据集相同,其中每次未被抽中的样本组成k 个袋外数据.

2)设原始数据变量个数为P,随机抽取m个变量作为子集分裂,利用CART 方法子集再进行分裂,每棵树进行自行生长,不剪枝,根据分枝优度准则选取最优分枝.

3)将生成的k 棵决策树组成随机森林,分别采取独立同分布的训练样本对每棵决策树进行训练,对结果进行投票或者取平均值得到新的回归分析或分类预测结果,即RF的最终结果.RF模型无需再进行专门的交叉验证,通常采用袋外数据在训练好的模型中进行模型测试.

3 Copula-RF变形监测模型

基于Copula-RF的大坝变形预测方法建模步骤如下.

步骤1:对实测数据利用图表法和统计学方法进行粗差剔除处理,为建立预测模型提供可靠的数据基础.

步骤2:采用Copula理论并选择合适的函数,对水位、气温等变量进行标准化处理并进行相关性计算,获得各变量间的相关性参数,对比得出准确的代表性影响因子.

步骤3:将处理后的数据作为原始样本集,优选出的影响因子及其推导量作为模型自变量样本集、测点的位移量作为模型因变量样本.

步骤4:采用boot-strap方法对进行随机抽样,获得模型袋外数据与训练样本；对不同参数之下所对应的袋外误差加以比对,甄选出其中误差最小时的m和n 值作为模型最优参数值；最终利用训练集建模,对测试集进行预测.

综上所述,基于Copula-RF算法的混凝土坝应力预测模型的建模流程如图1所示.

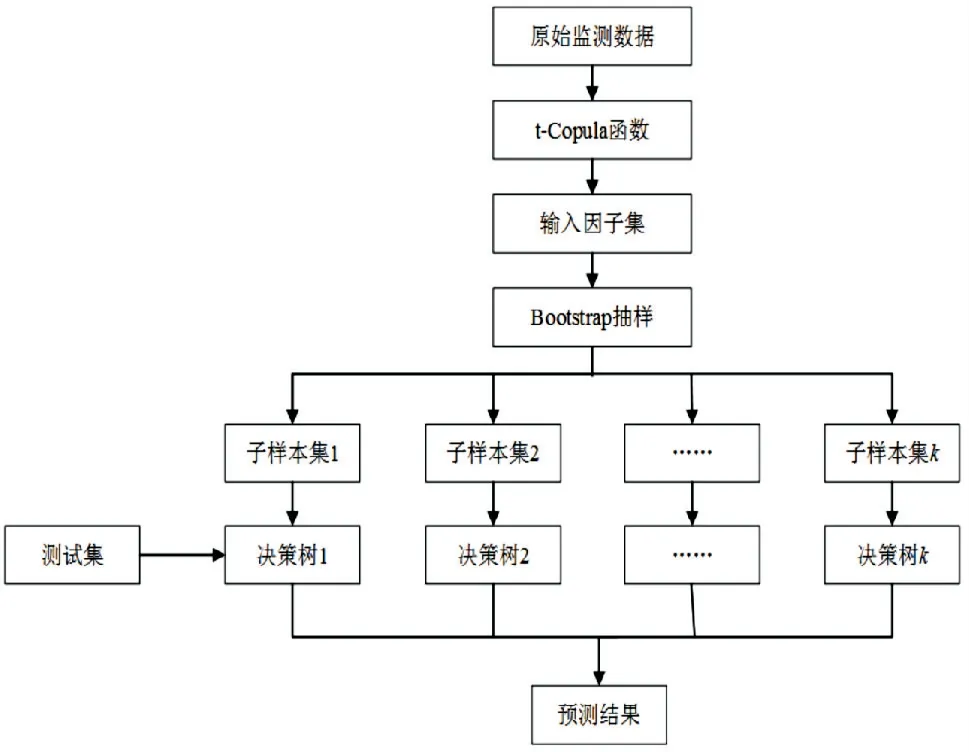
图1基于Copula-RF的混凝土变形预测模型流程图

4 工程实例

通过上述步骤,建立了Copula-RF大坝变形安全监控模型,并将其应用于某水利枢纽工程的监测数据分析工作中,以验证模型的有效性.该项工程水库总库容为4 700万m3,总装机容量为250 MW,设计洪水位633 m.工程由拦河坝、泄水建筑物、输水系统、地下厂房及地面开关站等建筑物组成.拦河坝为碾压混凝土重力坝,基础海拔562 m,最大坝高72.4 m,坝顶高程634.4 m,坝顶长206 m,坝顶宽7.5 m.

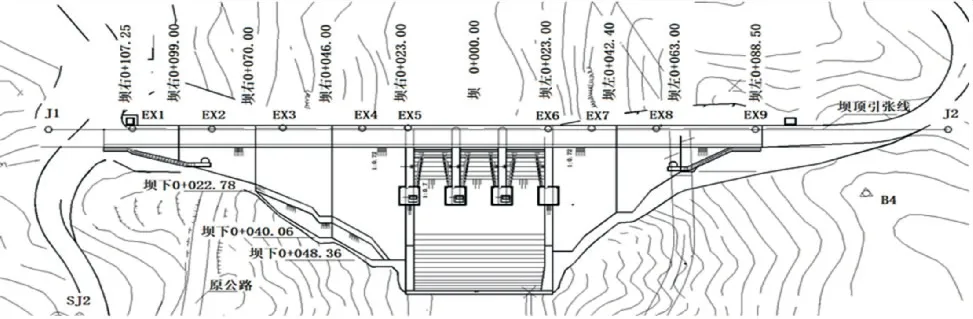
图2混凝土坝观测点平面布置图

该工程混凝土坝变形监测包括坝顶水平位移、垂直位移等项目.坝体共布置11个测点,其中工作测点9个,分设于每个坝段顶部；校核基点2个,分设于引张线左、右两端.坝顶水平位移监测采用引张线法,引张线固定端布置在坝右侧01+107.025处,导向端布置在坝左侧0+93.50处,全长200.75 m.引张线监测自动化系统的观测频率为1次/d.

4.1 预测模型输入因子的选择

通过资料分析和经验知识,混凝土坝变形主要考虑水压、温度和时效的影响,故引入水压因子HU、HD、(H-H0)1、(H-H0)2、(H-H0)3,温度因子T、T5、T20、T60、T90,时效因子θ、ln(θ),共12个备选因子,构成备选影响因子集:{HU,HD,(H-H0)1,(H-H0)2,(H-H0)3,T、T5、T20、T60、T90,θ、ln(θ)},其中:HU、HD分别代表上下游月平均库水位,H为观测日水深,H0为初始监测日水深；Ti为前i天温度平均值,i=5,20,60,90；θ 为资料初始监测日t0到观测日t的累计天数除以100,θ=(t-t0)/100.

为了准确获得具有代表性的输入因子,首先对原始环境数据进行预处理:粗差剔除和标准化(监测数据大小在[0,1]范围内),再运用Copula理论对监测数据进行非线性相关性检验.随后,将备选因子集作为X,将效应量即引张线EX7测点的水平位移(向下游为正,反之为负)作为Y.对备选因子进行筛选结果见表1.

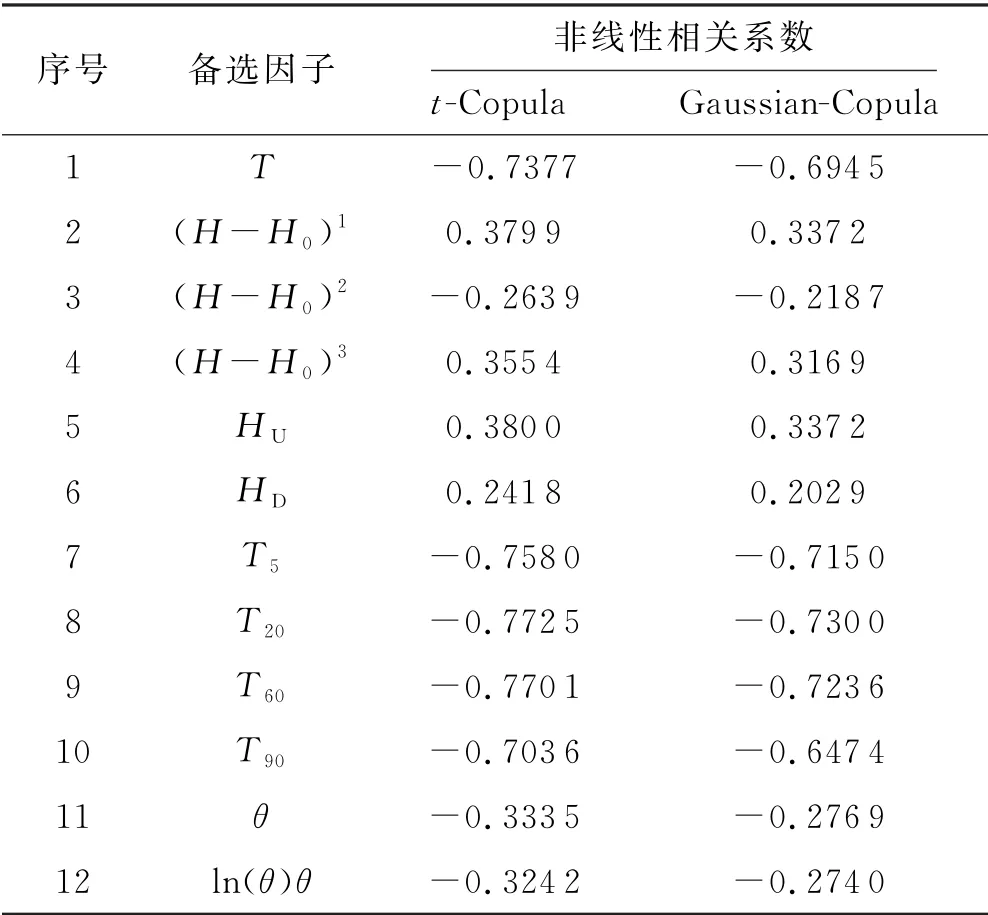
表1备选因子非线性相关系数

根据表1非线性相关性评价结果:t-Copula函数和Gaussian-Copula函数分析结果较为一致,两者相互验证,确保了分析结果的可靠性.但考虑到t-Copula函数对于随机变量之间的相关关系的变化敏感度更强,即非线性相关系数变幅较大,因此,t-Copula函数分析结果能更好地表达各因子间的关系.同时将非线性相关系数按照从大到小排列可知,(H-H0)2、HD和ln(θ)这3个因子的非线性相关系数明显小于其他因子,因此确定预测模型输入因子集为:{HU,(H-H0),(H-H0)3,T,T5,T20,T60,T90,θ}.

输入因子集中各因子相对EX7测点水平位移的相关程度分别为:0.38,0.379 9,0.355 4,-0.737 7,0.758 0,-0.772 5,-0.770 1,-0.703 6,-0.333 5.

根据模型输入因子集的选择,本文选取2016年6月2日至2018年10月22日实测数据(水压分量取2008年1月1日为基准日,坝前水深为68.81 m)作为自变量样本.坝顶引张线EX7测点水平位移实测数据为因变量样本.模型共869 组实测数据为总样本,其中选取719个样本作为训练样本,剩余150个样本作为测试样本,以此为基础进行基于Copula-RF的混凝土坝变形预测模型的应用研究.图3～5分别为水位、温度过程线及EX7测点水平位移过程线图.

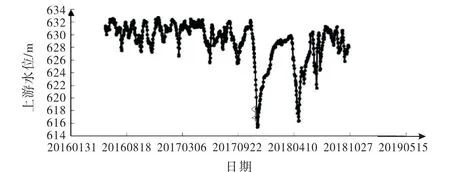
图3水位过程线图

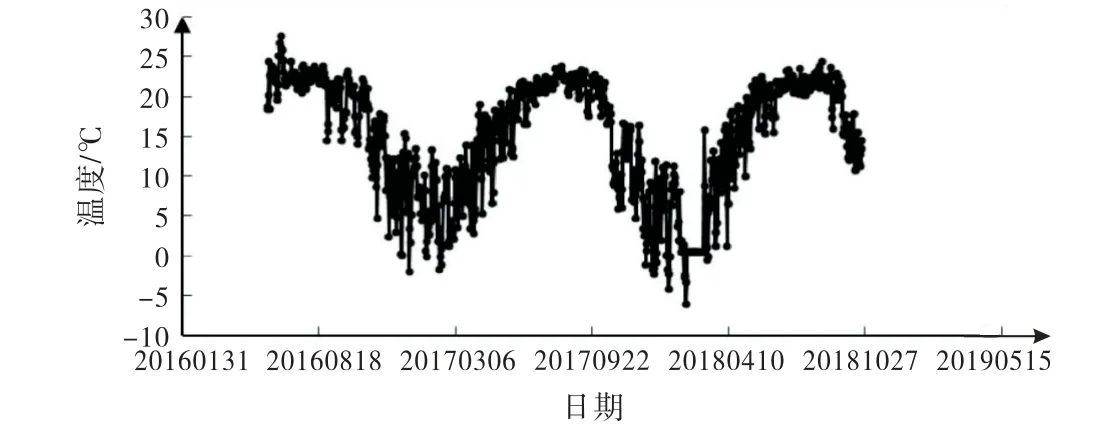
图4温度过程线图

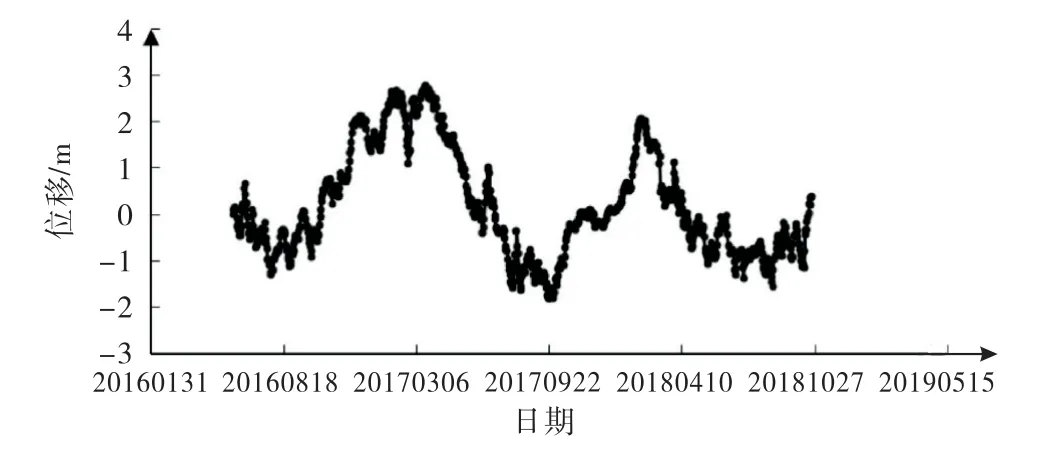
图5 EX7测点水平位移过程线图

4.2 模型参数选取

随机森林模型主要需设置两个参数:决策树的个数n 和决策树节点每次划分时随机抽取的候选变量个数m.本文通过试验得出决策树个数和袋外误差的关系曲线图,当决策树个数n为18时误差变小且趋于稳定,故n取18.当m=29时最优,图6为袋外误差和决策树个数关系图.

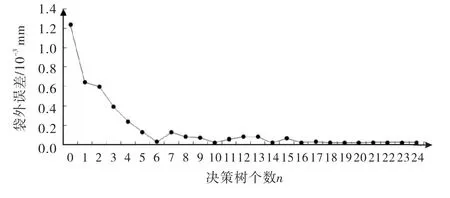
图6袋外误差和决策树个数关系图

4.3 混凝土坝位移预测结果

利用已训练好的Copula-RF模型,对经过处理和因子优选后标准化监测数据进行预测,并将预测结果与基于最小二乘回归的混凝土坝变形预测模型计算结果进行对比分析,结果如图7～9所示.

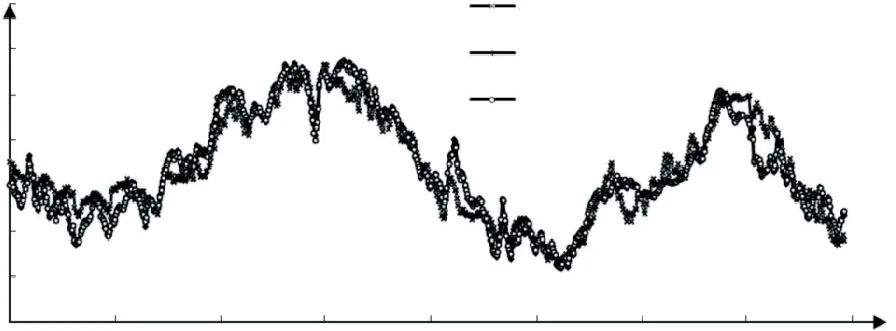
图7测点EX7各模型混凝土坝变形拟合值和实测值过程线

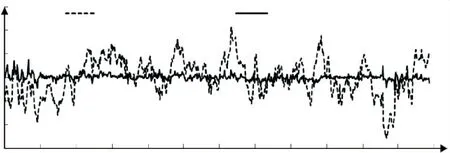
图8测点EX7各模型混凝土坝变形拟合残差效果

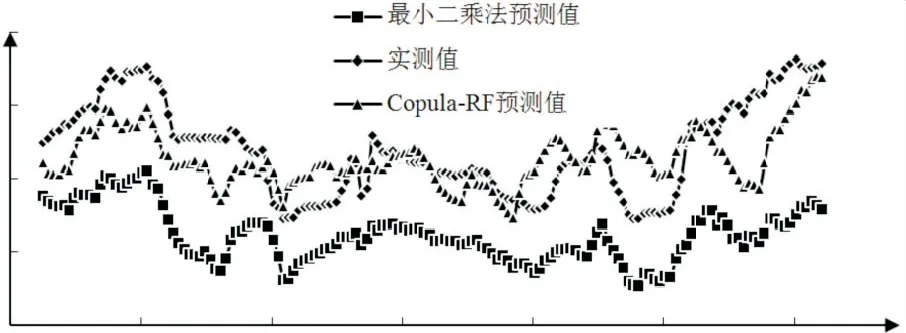
图9测点EX7各模型混凝土坝变形预测值和实测值过程线

由图7～9 可看出,与实测值对比.对于训练样本,其Copula-RF模型计算值与实测值过程线拟合效果好,训练期的位移在2.69～-1.77 mm之间变化,两者变化趋势基本一致.Copula-RF模型的拟合残差较小,拟合精度较高.对于预测样本,大坝实测水平位移在0.62～-1.5 mm之间波动,位移的实测值处于相对稳定的状态,Copula-RF模型的预测性能较好.

为了验证基于Copula-RF 的混凝土坝变形预测模型的有效性与优异性,将其与基于最小二乘回归的混凝土坝变形预测模型分析结果进行对比,采用均方根误差(RMSE)、平均绝对误差(MAE)及平均误差平方和(MASE)3个评价指标来衡量预测精度,各模型的评价指标计算结果见表2.由表2可知,利用本模型求得的三个指标比最小二乘法模型计算结果小,说明其预测精度及泛化性较好.

表2模型预测性能比较

因此,基于Copula-RF的混凝土坝变形监测模型预测变形值与实测值接近,且优于最小二乘回归方法,能够有效地实现混凝土变形趋势预测,本文所建立的Copula-RF的混凝土坝变形监测模型是切实可行的.

5 结论

考虑到混凝土坝变形监测数据具有非线性、非平稳等特点,本文采用Copula函数对各影响因子进行非线性相关分析,为建立随机森林模型提供最优因子集.相较于传统的基于最小二乘回归的混凝土坝变形预测模型,Copula-RF 模型具有较高的预测精度,与此同时,还能对泛化性加以有效保证.通过对OOB误差的使用,对泛化误差进行直接估计,无需对交叉验证的步骤加以延长,建立了混凝土坝变形预测的新模型.