基于运动学与离散元的边坡稳定性分析

赵健仓 来光 李永新 曹东勇 皇甫泽华

摘要：基于运动学分析的立体投影法对边坡工程的平面滑动、楔形滑动与倾倒破坏三种基本破坏模式进行了分析归纳。以某大型水利枢纽溢洪道高边坡为例，根据勘测成果筛选出优势结构面，采用立体投影法得到最大安全坡角，通过与现有自然坡角进行比较评估边坡的稳定状态，结果表明可能发生楔形体滑动，依据此滑动模式在3DEC中建立三维数值模型，进行了自然及暴雨工况下的稳定性分析。该方法将定性分析与定量分析相结合，可提高数值分析的针对性。

关键词：立体投影：边坡破坏模式：3DEC;最大安全坡角

中图分类号：TV221.2

文献标志码：A

doi：10.3969/j .issn.1000- 1379.2020.01.021

目前巖质边坡稳定性评价主要基于定性分析、定量分析和不确定性分析三类方法[1]。定量分析中极限平衡法应用广泛，然而其对实际问题的简化仍存在一定的主观性与局限性;数值分析需要建立复杂的应力应变模型，计算量大，耗时久，且无法保证计算结果收敛;不确定性分析则更多地需要借助已有监测资料，带有一定的经验性。定性分析中，运动学方法以其操作简便，直观易懂而成为解决该类问题的主要途径之一。

运动学是理论力学的一个分支学科，它是运用几何学的方法来研究物体运动的，通常不考虑力和质量等因素的影响[2]。其原理为运用立体投影及矢量代数理论，在赤平极射投影图中对坡面、优势结构面及摩擦角等几何要素进行投影，根据面面组合关系快速判断边坡稳定坡角。自20世纪60年代，各国学者运用运动学中的立体投影对由结构面控制的岩体边坡稳定性进行评价，取得了系统性的成果。Markland J T A[3]利用立体投影对钢性楔形体滑块的滑动模式进行了预测。Hocking G A[4]与Yoon W S等[5]则分别对四面楔形体的双平面滑动和多面斜坡破坏模式在立体投影中的分析方法进行了一定完善。Jeongi-Gi Um等[6]将块体理论与立体投影相结合起来对三峡永久船闸边坡的不连续岩体进行了运动学分析。Aksoy H等[7]在研究区域的数字高程模型（ DEM）的基础上，考虑不连续面，对楔形体和倾倒式破坏开展了运动学分析，弥补了赤平投影中低集中区域被忽视所造成的缺陷。王亮清等[8]则关注了双临空面边坡，并对其破坏模式进行了分类研究。陈剑文等[9]结合立体投影与极限平衡法对西源岭边坡的稳定性进行了评价。

笔者以河南省某大型水利枢纽溢洪道边坡为例，根据现场勘测成果，筛选出优势结构面，通过立体投影找到该边坡开挖的最大安全坡角，定性分析该岩质边坡的破坏模式。然后根据有限差分理论，利用FLAC3D将失稳的产状组合建立数值模型，进行天然、暴雨两种工况下的稳定性分析。将定性与定量分析相结合，既能得到边坡稳定的定量指标，又能提高数值分析的针对性和效率，为相似岩体边坡稳定性评价提供一种新的思路。

1 立体投影原理

立体投影法是进行运动学分析的一种有效工具，包括等面积投影与等角投影[10]。本文主要基于运动学分析单临空面边坡在平面滑动、楔形体滑动与倾倒破坏三种基本破坏模式下的最大安全边坡角α，与现有自然坡角对比来评估边坡的稳定状态。每种破坏模式下最大安全边坡角的确定方法分述如下。

1.1 平面滑动破坏模式

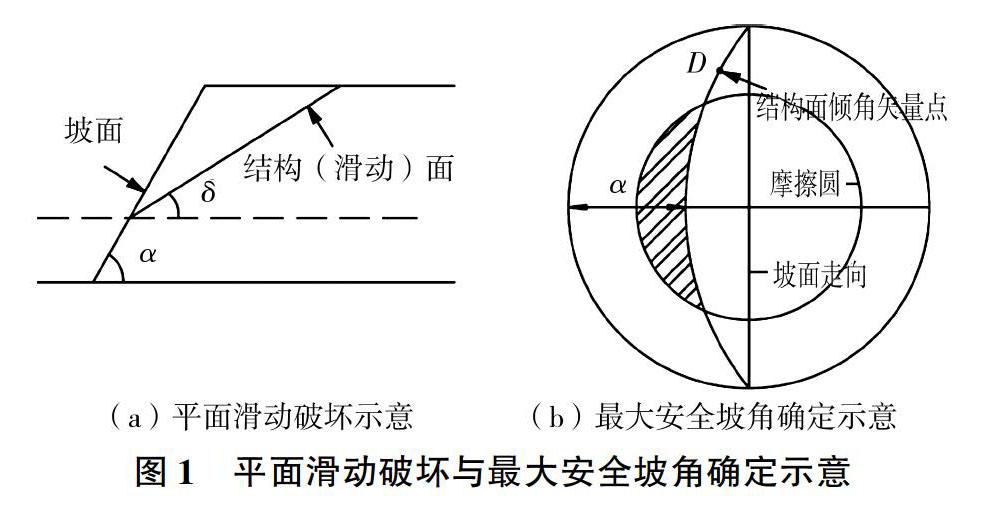
边坡的平面滑动指岩体沿某单一结构面发生失稳滑动，为最常见的岩体边坡失稳模式，该破坏模式需要以下3个条件[11]：①结构面的倾角δ大于内摩擦角φ而小于边坡坡角α（见图1（a））;②边坡中存在侧向切割面;③结构面的倾向与边坡倾向相同。平面滑动破坏模式下最大安全坡角的取值由边坡坡角、结构面内摩擦角和结构面倾角的空间关系决定，分为4种情况，见表1。

表1中最大安全坡角为“待定”时，具体确定方法如下：最大安全坡角等于通过设计边坡走向线与结构面倾角矢量点的大圆弧的倾角[12]，如图l（b）所示，D为结构面的倾角矢量。

1.2 楔形体破坏模式

楔形体滑动是指边坡沿两组结构面的交线或者沿一组结构面发生破坏[13]。其中沿一组结构面发生破坏可参考平面滑动确定破坏模式与最大安全边坡角。下面主要介绍沿结构面交线发生楔形滑动时破坏模式与最大安全边坡角的确定方法。楔形体滑动模式需要满足以下3个条件：①开挖坡角大于两组结构面交线倾伏角，而岩体内摩擦角小于前二者（见图2（a））;②坡面倾向与两组结构面交线倾伏向一致或相近。该种破坏模式的稳定状况依据坡角、结构面内摩擦角和两组结构面交线的倾伏角的关系不同，分为4种情况，见表2。

表2中最大安全坡角为“待定”时，具体确定方法如下：最大安全边坡角等于通过设计边坡走向线与结构面交线（在赤平投影图中用点表示）的大圆弧的倾角。

1.3 倾倒破坏模式

倾倒破坏常常出现在陡倾反向薄层岩层中，边坡岩体发生倾倒破坏需要具备以下条件：①结构面的倾角大于内摩擦角，边坡面的倾角不小于结构面法线方向的倾伏角与内摩擦角之和;②边坡倾向与结构面倾向相反（图3（a））;③结构面走向与边坡走向几乎平行或小角度相交。倾倒破坏根据坡面产状与结构面产状关系不同，分为4种情况，见表3。

表3中最大安全坡角为“待定”时，具体确定方法如下：在赤平投影图中，以坡面走向、倾角为小于坡角φ的产状画投影大圆，此投影大圆所代表的倾角即最大安全坡角。

2 实例分析

某大型水利枢纽主要建筑物包括大坝、溢洪道、泄洪洞等，溢洪道布置在左岸山体，开挖后溢洪道左岸边坡高达80 m，边坡主要涉及震旦系熊耳群弱风化安山玢岩，受区域地质作用岩体呈镶嵌碎裂结构，隐伏裂隙发育，边坡稳定性是决定工程正常运行的关键之一。综合原位试验、室内试验、经验类比等方法得到研究区的计算参数，见表4。依据现场调研及勘察报告，对工程区的结构面进行了统计，分析了其优势结构面的产状信息，共划分了5组优势结构面，见表5。

2.1 基于立体投影的边坡稳定性分析

根据以上给出的优势结构面情况分别对各段边坡进行破坏模式分析，确定不同破坏模式下最大安全坡角。

绘制各组结构面及坡面的立体投影图，见图4，内摩擦角为28°，边坡倾向130°，走向40°。

根据运动学原理，边坡发生平面滑动、楔形体滑动与倾倒破坏的最大安全坡角分别为75.47°（见表6）、38.67°（见表7）、63.00°（见表8）。剖面边坡开挖坡角为53.00°，可以看出，边坡平面破坏和倾倒破坏的最大安全坡角大于开挖坡角，在自然情况下边坡发生失稳破坏的可能性较小，但坡体可能沿J1、J4结构面交线产生楔形体破坏。

2.2 数值分析

依据立体投影分析结论，在3DEC中建立沿J1、J4结构面（无限延伸至坡脚处剪出）交线发生楔形体破坏的三维模型（见图5），模型长300 m、宽50 m、高113m。計算采用基于Mohr-Coulomb屈服准则[14]的弹塑性模型。天然工况下各岩土体介质材料计算参数见表4，暴雨工况时岩体参数在天然工况的基础上按80%折减。

通过3DEC强度折减法稳定性分析表明：楔形体破坏模式在天然工况下的边坡稳定性系数为1.18，边坡整体处于稳定状态;在暴雨工况下边坡稳定性系数为1.07，边坡整体处于临界稳定状态。位移计算表明：x向最大位移约为2.491 cm（见图6），主要集中于受结构面与坡面台阶切割形成的楔形体坡脚处，说明受多组切割面控制的楔形块体稳定性较差，易发生失稳滑动。z向最大位移约7.144 cm（见图7）.主要集中出现在坡顶位置。值得注意的是：J4结构面周围岩体的位移发生明显突变，建议对J4结构面加强现场监测。

由上述分析可知：算例边坡在天然和暴雨两种工况下分别处于稳定和临界稳定状态，与现场监测情况相符。立体投影法未考虑结构面间黏聚力c对岩体抗滑力的加成作用，故所得结论偏安全。

3 结论与建议

（1）采用运动学与离散元相结合的方法进行边坡稳定性评价，将定性分析与定量分析相结合，可减少数值建模计算的盲目性，提高计算效率。

（2）运动学方法与离散元计算结果对比表明，运动学方法仅考虑内摩擦角，而未考虑黏聚力对边坡抗滑力的影响，故结论偏安全，应结合定量分析计算进行修正才能更接近实际情况。

（3）优势结构面的力学参数是控制岩体稳定性的关键因素，建议增加原位试验研究。

参考文献：

[1] 董晓红，梁桂兰，徐忠厚，边坡稳定分析方法综述及发展趋势研究[J].水利与建筑工程学报，2012，10（5）：100-106.

[2]GOODMAN R E.Introduction to Rock Mechanics（ 2nd Edition）[M]. New York： John Wiley &Sons， Inc.， 1989：78-79.

[3]MARKLAND J T A.Useful Technique for Estimating theStability of Rock Slopes When the Rigid Wedge Sliding Typeof Failure is Expected[J].Imperial College of Rock Me-chanics Research Report， 1972， 19： 1-10.

[4] HOCKING G A.Method for Distinguishing Between Singleand Double Plane Sliding of Tetrahedral Wedges[J].Inter-national Joumal of Rock Mechanics and Mining Sciences&Geomechanics Abstracts， 1976， 13（7）：225-226.

[5]YOON W S，JEONC U T，KIM J H.Kinematic Analysis forSliding Failure of Multi-Faced Rock Slopes[J].EngineeringGeology， 2002， 67（1/2）： 51-56.

[6] JEONGI-CI Um， KULATILAKE P H S W. Kinematic andBlock Theory Analyses for Shiplock Slopes of the ThreeGorges Dam Site in China[J].Geotechnical and CeologicalEngineering， 2001， 19（1）：21-42.

[7] AKSOY H， ERCANOGLU M.Fuzzified Kinematic Analysisof Discontinuity-Controlled Rock Slope Instabilities[J].En-gineering G eology，2007， 89（ 3/4）： 209-219.

[8] 王亮清，KULATILAKE P H S W，唐辉明，等，双临空面岩质边坡滑动与倾倒破坏的运动学分析[J].岩土力学，2011，32（增刊1）：73-77.

[9] 陈剑文，李辰州，基于赤平投影法的西源岭边坡稳定性分析[J].防灾减灾工程学报，2014，34（4）：437-442.

[10] 杨天鸿，张锋春，于庆磊，等，露天矿高陡边坡稳定性研究现状及发展趋势[J].岩土力学，2011，32（5）：1437-1472.

[11] 吴绍强，极射赤平投影法在岩质边坡稳定性分析中的应用[Jl.西部探矿工程，2009（ 10）：117-121.

[12]周培峰，谷飞宏，谭维佳，赤平投影法确定稳定边坡角[J].中国水运，2011，11（ 11）：267-268.

[13] 张学东，刘向飞，衣雪峰，等，岩质边坡稳定性的运动学分析[J].水利水电工程设计，2017，36（2）：50-53.

[14] 沈金瑞，林杭，多组节理边坡稳定性FLAC3D数值分析[J].中国安全科学学报，2007，17（1）：29-33.

【责任编辑 张华岩】

收稿日期：2019- 05 - 08

基金项目：河南省水利科技攻关计划项目（GG201652）

作者简介：赵健仓（1967-），男，河南方城人，高级工程师（教授级）.主要从事水利工程勘察方面的研究工作

通信作者：来光（1971-），男，河南洛阳人，高级工程师（教授级）.主要从事水利工程勘察方面的研究工作