几何画板优化二次函数图像与性质的教学

叶少静

【摘要】几何画板凭借其快捷计算，精准作图，动态演示效果，大量数据处理等优势，能更好地优化数学教学。运用几何画板把抽象的教学内容具体化，直观化，动态化，更好地把数形结合的数学思想渗透到教学中去。本文结合教学实践，阐述几何画板在二次函数图像与性质的教学中具体应用，促进几何画板和传统教学的有机结合，更好地击破教学重难点，提高课堂效率。

【关键词】几何画板;动态化;优化

二次函数在初中教学中占据很重要的地位，也是多年中考的热点之一。其中二次函数的图像与性质这一节学习显得尤为重要，可这部分内容比较抽象，在传统教学中，缺少形象直观的教学情境，常常遇到老师讲不清，学生不容易理解和消化的情况。学生对知识点含糊不清，只能被动接受老师所讲的内容，依靠机械式记忆来完成学习任务，没能达到理想的效果。

二次函数图像与性质教学中，传统课堂教学往往采用如下的教学过程：第一步：指导学生用五点作图法（列表、描点、连线）在练习本上作出几个典型的二次函数图像。第二步：引导学生结合所作出的图像，仔细观察图像的特点，猜想函数图像的基本特征。第三步：通过几个典型的二次函数图像，结合刚才的猜想，归纳出函数图像的性质。

这样的教学过程也能培养学生观察，猜想，归纳和概括的能力，让学生经历由特殊到一般，再由一般到特殊的过程，符合学生的认知规律.但是在教学实践中往往遇到以下问题：

1.由于取点过少，学生的作图常常出现折线，并没有形成光滑的抛物线。不规范的作图，不利于后面观察二次函数图像与性质。

2.单凭几个有限的点，学生很难理解二次函数的图像是抛物线。无法画出二次函数完整的图像。

3.仅从几个典型的函数图像中，归纳出二次函数图像的性质。大部分学生很难准确归纳出图像的性质和变化规律。不容易从静态的函数图像，发现其动态的变化关系。理论的说教在这往往没有说服力。

笔者通过教学实践发现，几何画板能弥补这些不足。在二次函数图像与性质课堂教学中，充分发挥几何画板在数字计算，生成函数图像以及动态呈现函数图像变化的优势，把几何画板融合到传统的教学中，使学生更全面理解函数图像的生成以及图像变化与系数之间蕴含的关系，有助于学生对此知识的理解更深刻。下面以九年级上册《二次函数图像与性质》一节为例，谈谈几何画板对于二次函数图像与性质教学的帮助。

教学目标： 1.学生能够使用描点法画出二次函数y=ax2的图像;2.学生通过对二次函数y=ax2图像的观察分析，理解其性质特征。

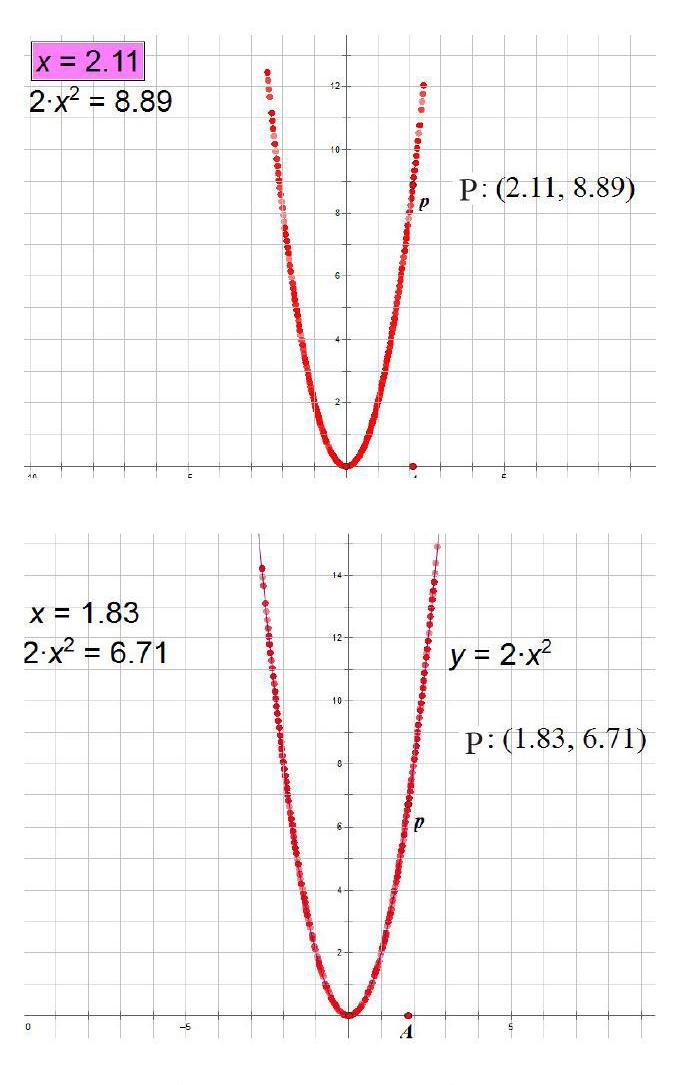
活动一：借助几何画板，通过跟踪点的轨迹，动态演示二次函数生成过程。初步了解二次函数的图像。

具体步骤如下：1.在菜单栏上选择[绘图]菜单，下拉菜单中选择[定义坐标系]，在画板上创建坐标系;2.在x轴上构造一个点A，度量其横坐标，把标签修改为x;3.在菜单栏上选择[数据]菜单，计算2x2;4.在菜单栏上选择[绘图]菜单，绘制点P（x，2x2）;5.选中点P， 在菜单栏上选择[显示]菜单，选择跟踪绘制点。拖动点A，观察点P的运动路线。选择生成点P的动画;6.在菜单栏上选择[绘图]菜单，绘制新函数y=2x2，在观察函数图像与动点p经过的路线。

设计意图：几何画板动态地呈现无数个点形成抛物线的过程，点动成线的过程一目了然，让学生体会函数生成的过程。静态的函数关系通过几何画板动态地呈现出来，学生更容易接受和理解。

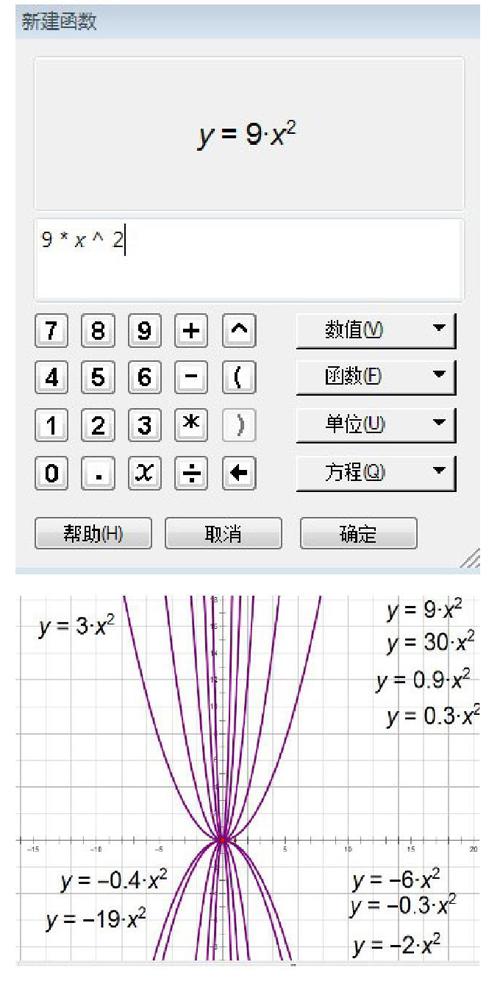
活动二：老师接着追问所有二次函数的图像都是抛物线吗？这时我们可以借助几何画板强大的计算功能和绘制函数功能。

让学生亲自动手操作，任意输入一个二次函数解释式，利用几何画板绘制函数图像，再让学生观察所得函数图像是否都为抛物线。

设计意图：借助几何画板创造了一个让学生动手，亲身体会的平台，学生可以通过几何画板快速绘制任意的二次函数，从大量的图像中得出二次函数图像是抛物线，不再局限于有限个典型的函数图像，这样更有说服力，解除学生的疑惑。这个教学过程不再是学生被动地接受知识，而是主动地观察和发现规律，弥补了传统教学上的不足。

活动三：让学生在学案纸上，做出二次函数y=x2和y=-x2的图像。

通过几何画板演示二次函数的生成过程，学生大致了解二次函数图像，再让学生动手作图，学生的作图会比较接近抛物线，也更顺利完成作图。

设计意图：

通过描点法做出二次函数y=ax2的图像是本节课的教学目标之一，让学生动手作图，更深刻地理解二次函数的图像，也为后面研究其图像性质打下基础。

活动四：1.观察y-3x2，y=6x2，y=0.5x2的图像，分别从图像的形状，开口方向，对称轴，最大（小）值，增减性方面考虑，引导学生找出几个函数图像的共同点。

猜想：二次函数y=ax2（a<0）图像性质

（1）图像成轴对称图形，对称轴为Y轴。

（2）开口方向：向上。

（3）对称轴左边：y随x的增大而减小;对称轴右边：y随x的增大而增大。

（4）顶点坐标：（0，0） 。

（5）最低点（最小值）。

通过几何画板动态演示，验证学生的猜想：（1）构造图像上的一点A'，把y轴标记镜面，再作点A的反射点A'。观察发现点A与A'都在二次函数图像上，说明该图像关于y轴对称。度量A与A'的坐标，运动时可以观察两个对称点的坐标变化。

（2）选取一个点B，度量横坐标和纵坐标。当移动点B时，观察其坐标的变化。在对称轴左侧，横坐标变大，纵坐标变小;在对称轴右侧，横坐标变大，纵坐标也变大。

（3）当点B移动到顶点时，纵坐标最小，取最小值。

2.利用几何画板强大的计算功能和函数生成的功能。任意新建几个二次函数y=ax2（a<0）的图像。學生小组合作，用类比的数学方法，探究并归纳其图像性质。

老师引导学生归纳二次函数图像的性质，并填下表：

设计意图：让学生经历“观察、猜想、验证、总结”的过程，鼓励学生主动参与，提高学生动手能力。小组合作的形式，借助几何画板验证函数图像性质的猜想，在老师的引导下，归纳和总结函数图像性质，从中感受数形结合的数学思想。

活动五：利用几何画板探究系数a对二次函数y=ax2（a<0）图像的影响。

具体步骤如下：1.在菜单栏上选择[绘图]菜单，在下拉菜单中选择[定义坐标系]，在画板上创建坐标系;2.在x轴上构造一个点C，过点C作x轴的垂线，在x轴上取一点A，度量其纵坐标，把标签修改为a;3.在菜单栏上选择[数据]菜单，计算y=ax2并绘制新函数。老师拖动点A运动，让学生观察运动过程中，a的数值变化，以及系数a的变化对函数图像产生的影响。

老师演示完后，让学生动手操作，体会当改变a的取值，y=ax2图像将如何变化。

归纳：（1）系数a决定二次函数图像开口方向，当a<0，开口向上;当a<0，开口向下。

（2）a的绝对值大小决定开口大小：a的绝对值越大开口越小;                                  a的绝对值越小开口越大。

设计意图：学生动手操作，通过大量的图像变化演示，亲身体会到系数a的变化对函数图像形状的影响。

以上五个教学活动，环环相扣，高效地完成本节课的教学任务。借助几何画板可以将原来静止的函数图像动起来，从而让学生更直观地看到二次函数与其图像之间的对应关系，轻松化解了本节课的教学重难点。我国著名数学家华罗庚曾说过：“数缺形时少直观，形少数时难入微;数形结合百般好，隔离分家万事休。”提醒教师要设法把抽象难懂的理论知识转化为形象直观，便于学生发现和接受，帮助学生化解学习难点，激发学生的学习兴趣和热情。在老师的指导下，让学生在学习中探索，在学习中发现，在学习中总结。

作为一线教师，要走在教学的前沿，不断钻研教材的同时，学习和接纳一些创新的教学手段和教学方法。让多媒体教学更好地辅助传统教学，两者优势互补，相辅相成。

参考文献：

[1]杨泽忠.论计算机辅助中学数学函数图像的教学[J].电化教育研究.

[2]李铭.用几何画板解决二次函数的教学难点[J].中学数学参考，2010（2）.

[3]胡翔.透析几何画板在初中二次函数教学中的应用[J].理论探索，2017（08）.

[4]崔恒刘.借几何画板突破教学“一次函数图像”的难点[J].教学导航，2013（1）.

[5]王宗信.利用几何画板探究一次函数的图像及其性质的实验设计与思考[J].中国数學教育，2012（5）.