学案:催生高效数学课堂
孙玲

[摘 要] 学案是学生学习的起点、指南针,也代表着学生学习的目的地. 以“向量的概念及表示”一课为例探讨学案的运用,以使学案最大化地发挥作用,实现高效的课堂.
[关键词] 学案;高中;数学;高效;课堂
教育家吕叔湘说:“学生的学,应当由被动地学向主动地学转化.”新课改强调以学生为主体,尊重学生个体差异,注重师生交流互动,让学生有一个快乐的学习过程. 于是乎,学案应运而生. 学案是学生学习的起点、指南针,也代表着学生学习的目的地. 教师该如何用好学案,使学案最大化地发挥作用,实现高效的课堂呢?本文以“向量的概念及表示”一课为例,加以说明,供大家参考.
目标要求,明确学习目标任务
做任何事情都要有明确的目标,有了目标才会有动力. 学习也不例外,所以,学案在一开始就应将一节课所要达成的目标指出,让学生了解这节课所要到达的目的是什么,才能积极主动地参与到课堂中,这是高效课堂的前提条件.
(1)从知识角度来看,要求了解向量是在什么背景下产生的,理解什么是平面向量和向量如何用几何方法来表示;掌握平面向量的有关概念,要学会正确辨别平行向量、相等向量和共线向量三者之间的区别与联系.
(2)从能力角度来看,要求学生通过对平面向量的学习与研究,初步认识现实生活中的向量和数量有着本质的区别.
(3)从培养情感的角度来看,让学生通过对向量与数量的辨别,培养他们认识客观事物的数学本质的能力.
预习引导,提供自主学习的平台
“先学后教”是江苏泰兴洋思中学的成功教学模式. “先学”是指学生现根据学案进行自学,在学生自学的基础上,教师再“教”. 我校课堂学案的“预习引导”这一环节很好地体现了这一模式.
【预习引导】
预习教材P59~60的内容,并思考下列问题:
(1)用什么样的数学模型来刻画位移、速度、力这样的量?
(2)向量的定义是什么?向量与数量有什么区别?
这样的设置,很好地引导学生进行自学,也从根本上解决了学生预习什么内容,应当预习到什么程度的问题. 有了学案,学生的自学过程就不再盲目. 学案帮助学生明确学习内容、要求,带着问题阅读课本、寻找答案,在这一过程中就对新知识有了一定的把握和认知,从而提高了课堂效率.
教学过程,搭建高效课堂结构
在让学生先学的基础上,课堂便是教师的“教”. 所谓教师的“教”并不是与传统课堂模式一致的“填鸭式教育”,而是要根据新课改要求,将数学充分联系到实际生活,然后在教师的帮助下,由学生将生活化的知识转化为数学的知识,体现数学来源于生活的理念.
【教学过程】
(一)情境设置
一个质量m=60 kg的物体放在光滑的水平面上,在与水平方向成α=60°角斜向上的拉力F=10 N的作用下向左运动了5 m,求拉力所做的功.
物理中的标量和矢量对应数学中的数量和向量. 问:再举出一些向量和数量.
数量:距离、质量、身高、时间、密度以及体检中的视力、 肺活量等.
向量:位移、力、速度、加速度等.
(二)生成概念
1. 向量的概念:__________.
2. 向量的表示方法:
(1)几何表示:__________ .
(2)用字母等表示:__________.
3.向量的有关概念:
(1)大小:①向量的模:__________. ②零向量:__________(思考:0与0的含义与书写区别);③单位向量:________. (思考:平面直角坐标系内,起点在原点的单位向量,它们的终点的轨迹是什么图形?)
(2)方向:平行向量:__________.
(3)大小与方向:①相等向量:____. 如:在平行四边形ABCD中,=. 向量是否相等只与大小和方向有关,与起点无关.②相反向量:__________. 规定:__________.
(三)理解和巩固
例1:如图2,正六边形ABCDEF的中心为O,在图中带有箭头的线段表示平面向量,试问在它们中:
(1)有哪些向量与共线?
(2)有哪些向量与相等?
(3)向量与向量是否相等?请说出理由.
教案不是先给出相等向量、平行向量、共线向量、相反向量的定义,而是让学生在自己的观察中产生这些概念,使概念成为学生观察、归纳的自然产物,而不是教师规定、灌输的知识. 虽然有的教师认为这样做会浪费课堂时间,降低课堂效率,但是让学生经历概念的生成过程,才能对概念理解得更加深入,这才是真正意义上的高效课堂.
數学运用,助力突破重点、难点
数学应用,是学习数学的最终归宿. “数学运用”中例题与习题必须精挑细选. 因为内容的作用不可小觑,它旨在帮助学生加深概念的理解,突出重点,冲破难点. 本节课的重点与难点都是对向量概念的理解. 在初步掌握向量概念的基础上,教师可以在学案中通过例题进一步完善学生对向量概念的理解.
【数学应用】
首先,将例1进一步引申:
(1)除外,图2中所给7点的连线中,与共线的向量有几个?与相等的向量有几个?
(2)除外,图2中所给7点的连线中,与互为相反向量的向量有几个?
接着,让学生完成下面的两个例题,并作交流.
例2:如图3所示的4×5方格纸中向量与,它们的起点与终点分别是哪个点?它们是相等向量吗?你能以图中的格点为起点和终点画出多少个与长度相等、方向相反的向量?请试一试.
例3:请分别说出下面三种情况中各向量的终点的集合所表示的图形.
(1)所有的方向相同的向量平移到同一条直线上;
(2)所有单位向量具有同一个起点;
(3)把所有的平行向量的起点移到同一个点上.
为了进一步实现数学应用的能力提升,师生合作完成例4,让学生初步感受平面向量在平面几何中的应用.
例4:如图4,已知四边形ABCD中,M,N分别是BC,AD的中点,又=. 求证:CN与MA平行且相等.
通过本例,让学生掌握利用向量相等或共线证明平行、相等问题:
(1)证明线段相等,只需证明相应向量的长度(模)相等;
(2)证明线段平行,先证明相应的向量共线,再说明线段不共线.
问题是数学的心脏. 在学案中,例题与习题是学生发现问题、解决问题的载体,因此教师必须精心设计,一是不能脱离教学目标,二是有利于学生认知水平的提高. 设计的题目应具有代表性,要精准并具有一定的灵活性,要注意难度的设计,做到拾级而上,有利于思维的启迪和题型的变化等. 此外,针对学生在学习中普遍存在的问题,教师要设计一些针对性较强的补偿性练习让学生加以巩固,以达到提高学生的薄弱环节的目的.
课后反馈,及时检验学习成果
学案添加了“课后反馈”这一环节,有利于帮助学生对学案进行充分的学习,及时地对所学知识进行归纳总结、复习回顾、加深记忆、巩固知识. 如果长期坚持,必定能真正发挥导学案的功效,使学生实现高效学习.
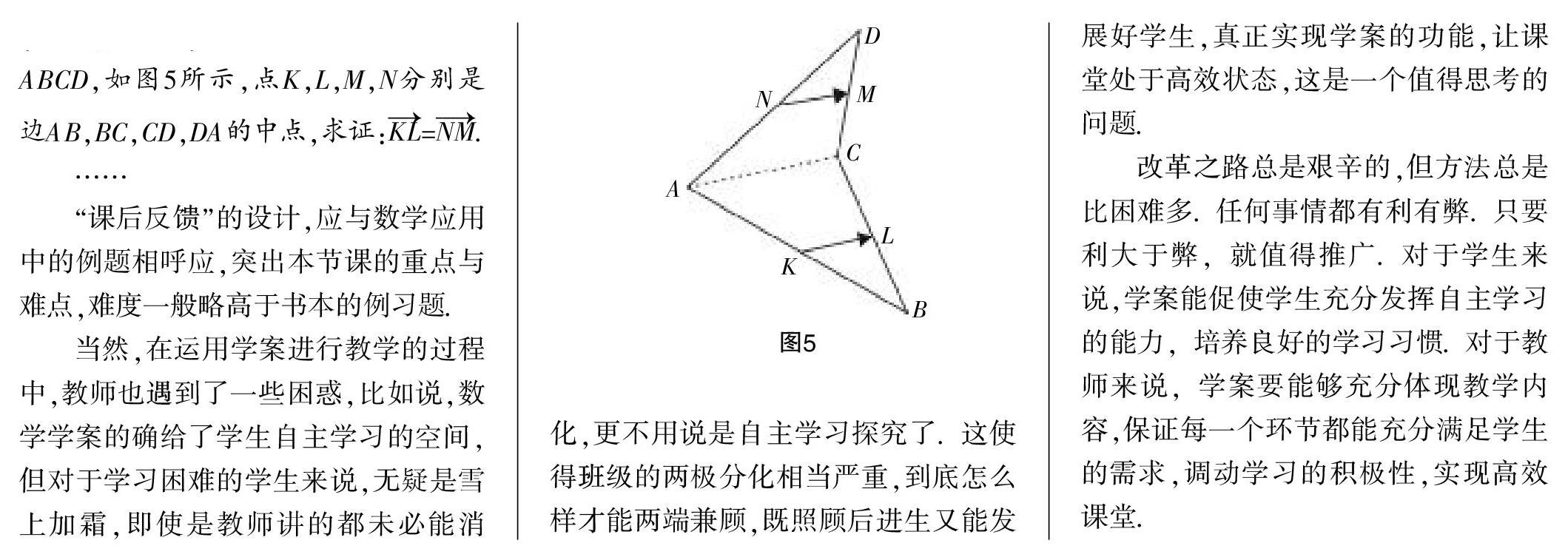
【课后反馈】(撷取部分)
“课后反馈”的设计,应与数学应用中的例题相呼应,突出本节课的重点与难点,难度一般略高于书本的例习题.
当然,在运用学案进行教学的过程中,教师也遇到了一些困惑,比如说,数学学案的确给了学生自主学习的空间,但对于学习困难的学生来说,无疑是雪上加霜,即使是教师讲的都未必能消化,更不用说是自主学习探究了. 这使得班级的两极分化相当严重,到底怎么样才能两端兼顾,既照顾后进生又能发展好学生,真正實现学案的功能,让课堂处于高效状态,这是一个值得思考的问题.
改革之路总是艰辛的,但方法总是比困难多. 任何事情都有利有弊. 只要利大于弊,就值得推广. 对于学生来说,学案能促使学生充分发挥自主学习的能力,培养良好的学习习惯. 对于教师来说,学案要能够充分体现教学内容,保证每一个环节都能充分满足学生的需求,调动学习的积极性,实现高效课堂.

