二极管单平衡与双平衡电路输出性能分析与比较

胡 毅，董晓雅，张 勇，王亚文，邓志旭

（滁州学院，安徽 滁州 239000）

0 引言

在高频电子线路中，二极管平衡电路以其结构的简单性以及输出信号性能优良等特点得到了广泛的应用［1-3］。它主要利用二极管的非线性效应来实现信号相乘的功能，并通过多个二极管所构成的平衡电路结构来抵消大部分无用的非线性成份，从而使得输出信号性能得到较好改善［4］。从频域角度来看，利用二极管平衡电路可以实现频谱不失真搬移，同时通过平衡电路的自我抵消功能可消除大部分无用频率成份，从而达到有效改善输出有用信号的目的［5，6］。在通信系统中，利用二极管平衡电路的这种频谱搬移以及信号抵消特点，可实现振幅调制以及信号混频等功能［7］。

二极管平衡电路具有单平衡和双平衡两种形式［5］，而对于不同的平衡电路，其输出信号参数的计算方法以及由这些参数所得到的性能特点也并不相同，这会给应用带来不便。对此，首先利用所给二极管单平衡与双平衡电路结构，给出两种电路在线性时变模型下输出电流参数的计算方法；然后基于该参数进一步给出输出有用信号功率、信号隔离度等性能参数的仿真计算结果，并进行对比分析。通过这种方法的处理，可以对二极管平衡电路有一个较好的理解，同时也可为相关二极管平衡电路的设计与应用提供一些参考。

1 二极管线性时变模型

令v1与v2为同时加到二极管两端的两个交变信号，考虑到二极管的非线性效应［8］，则二极管的伏安特性可写为i=fV(Q+v1+v2)，其中VQ为二极管静态工作点电压。对电流i进行泰勒级数展开，有

其中f(n)(VQ)为i=f(v)的n阶导数在VQ点的取值。

式（1）中若v1的信号强度远大于v2，则i可近似用线性时变模型给出［5］，即

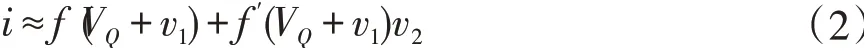
式（2）中右边的第二项包含了信号相乘的结果，利用其二极管单平衡或双平衡电路即可实现载波调制或信号混频等功能，同时，通过式（2）还可进一步得到其他一些性能参数。

另外，在式（1）中，若 令v1=V1cos(ω1t)，v2=V2cos(ω2t)，则可推导出输出电流i的频率通式为其 中（0 ≤k1≤n-m）和q= |m-2k2（|0≤k2≤m）均取非负整数；而当设置V1≫V2时，式（1）将转变为式（2）所给的线性时变方程，进一步可推导出此时电流i的频率通式为由此可知，在改变v1与v2两信号的强弱关系时，可有效消除大量无用频率成份的影响。

在利用二极管非线性效应进行振幅调制或混频时，最终所需的有用输出信号频率为它表明由上面线性时变模型所给的结果，还必须通过进一步处理才能得到比较纯净的有用信号，而这可通过二极管平衡电路并配合一定的滤波器来实现。

2 二极管单平衡与双平衡电路分析与参数计算

2.1 二极管单平衡电路结构

对于二极管单平衡电路，其主要利用两个平衡支路上的二极管非线性效应来实现信号相乘并获取有用信号，其结构如图1 所示。在图1 中，vr与vs分别为输入到两相同二极管D1与D2的强信号（或控制信号）与弱信号；变压器T1副边与T2原边从中间均抽出一个抽头，分别与两个二极管构成两个回路，且两变压器T1与T2的原副边各部分匝数比均为1:1。

2.2 二极管单平衡电路输出电流计算

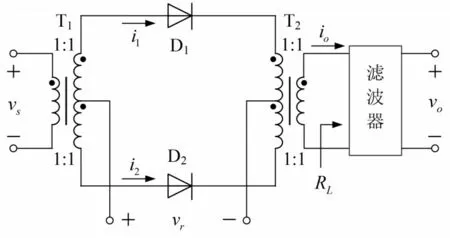
图1 二极管单平衡电路

利用基尔霍夫回路电压定律以及节点电流定律，可得当vr＞0，即vr处于正半周时（2kπ-π 2 ＜ωrt＜2kπ+π 2，k∈ℤ），图2中i1与i2两回路电流满足方程：

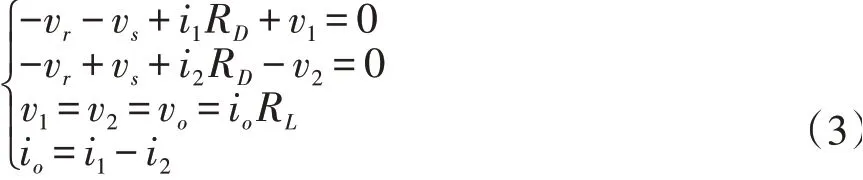
式（3）中最后一项是利用T2变压器上半部分与下半部分磁通方向相反得到的。通过求解式（3）可得输出电流

当vr＜0，即vr处于负半周时由于D1和D2均被vr控制为反向截止状态，因而此时io=0。

考虑用K1(ωrt)来表征io在一个完整周期的情况，并进行傅里叶级数展开，有

图2 二极管单平衡电路在vr正半周时的等效电路

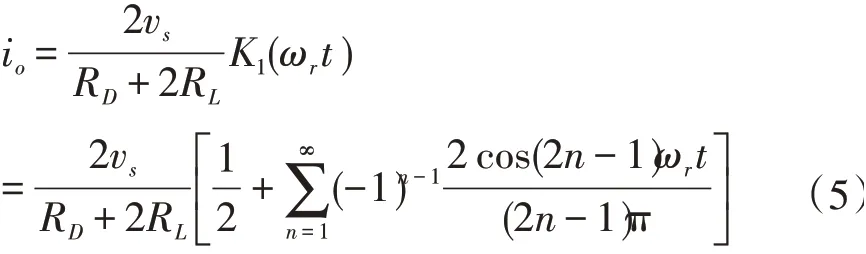
由式（5）可知，此时输出电流io的频率通式为其 中p′取0 和 正 奇 数。对 比取非负整数）可知，利用二极管单平衡电路可进一步消除输出信号中ωr的偶次项无用频率成份，从而可提高输出信号的性能，并降低对后端滤波器的设计要求。

当将图1 二极管单平衡电路用作混频器时，考虑到vs=Vscos(ωst)且通常有RL≫RD，这样由式（5）可得到频率为ωIF=ωr-ω（s或ωs-ωr）的中频输出电流为

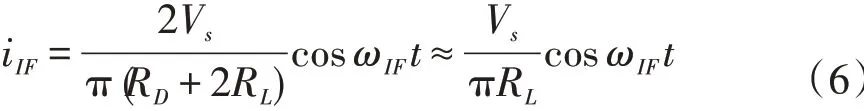
2.3 二极管双平衡电路结构

二极管双平衡电路结构如图3 所示，其与单平衡电路总体相似。但与单平衡电路不同的是，在强信号vr处于负半周时，单平衡电路输出电流io=0，而对于图3中的双平衡电路，输出电流io与vr处于正半周时的电流情况相类似，只是方向相反。

2.4 二极管双平衡电路输出电流计算

图3 二极管双平衡电路

在图3中，当vr处于正半周时，二极管双平衡电路中D1与D2导通，D3与D4则处于截止状态，此时等效电路与图2 相同，输出电流io同样可由式（5）给出；而当vr处于负半周时，二极管D3与D4导通，而D1与D2则处于截止状态，此时等效电路如图4 所示，相应地i3与i4两回路电流满足方程

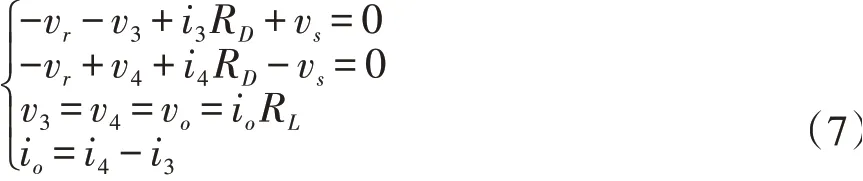
求解式（7）可得

这样综合式（5）与式（8），可得在控制信号vr一个完整周期内的输出电流为

由式（9）可知，此时输出电流io的频率通式为其中为正奇数。这表明，相对于单平衡电路，双平衡电路可进一步消除输出信号中无用频率ωs的影响，因而使得输出信号性能更好。

同样，如果将二极管双平衡电路用作混频器，则由式（9）可得此时输出中频电流

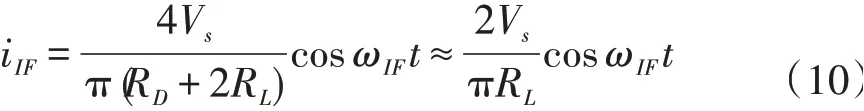
3 二极管单平衡与双平衡电路相关性能参数仿真比较

为进一步了解两种平衡电路的性能，除上文所给的输出电流和功率参数外，还需了解其他一些参数性能。这里以二极管平衡电路的应用——混频器为例，通过仿真分别给出两种电路的混频输出信号频谱性能以及端口隔离度等仿真比较结果。

仿真采用LTSpice 电路仿真软件并结合MAT⁃LAB 数据处理软件来进行。设计的双平衡仿真电路及相关元件参数如图5所示。由于单平衡电路只需移除双平衡电路中D3 与D4 两元件即可得到，此处不再具体表述。

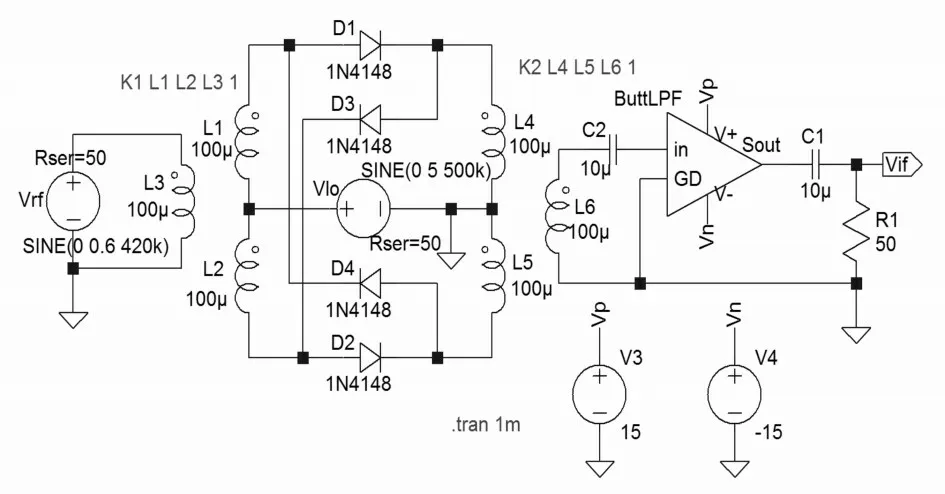
图5 二极管双平衡仿真电路

图5 中信号参数设置为：射频输入vrf的幅度为0.6V，频率为420kHz；本振vlo的幅度为5V，频率500kHz；输出中频vif的频率为80kHz。此外，两电路中所用的滤波器均为巴特沃斯（Butterworth）低通滤波器，其参数设计为：通带截止频率为80kHz，阻带截止频率为420kHz，通带增益为0dB，阻带最大衰减为-45dB。

3.1 输出信号频谱性能比较

利用图5 所得到的单平衡和双平衡电路，在无低通滤波器时，两电路输出信号频谱分别如图6（a）与6（b）所示；而在经巴特沃斯低通滤波器滤波后，两电路输出信号的频谱则如图7（a）与7（b）所示。

从图6（a）与6（b）的比较中可以看出，在无滤波器的情况下，双平衡电路由于抵消了更多的无用频率成份，因而在波形上比单平衡电路更为平滑些。而在经滤波器滤波后，两个电路的输出性能都可得到有效提高，如图7（a）与7（b）所示；但同时可以看出，在相同的输入信号与滤波器下，双平衡电路输出信号性能同样要明显好于单平衡电路。

3.2 端口间信号隔离度性能比较

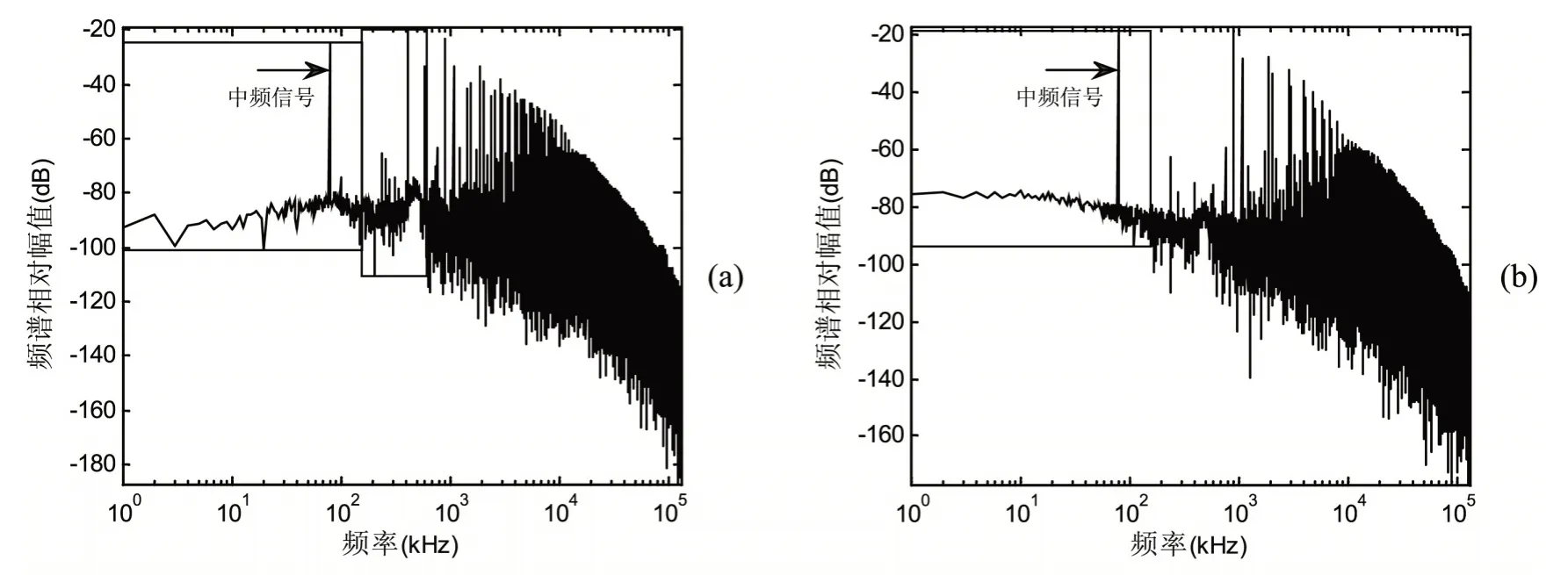
图6 无滤波器时输出频谱图：（a）单平衡电路;（b）双平衡电路

图7 滤波器滤波后输出频谱图：（a）单平衡电路;（b）双平衡电路

当单平衡和双平衡电路用作混频器时，各端口间的信号隔离度也是其重要性能指标之一。根端口间信号隔离度的定义其中P12为从1 端口串通至2 端口的功率，利用图5 得到的单平衡和双平衡电路，通过仿真计算出的一些主要端口间的信号隔离度如表1所示。

从表1 中可以看出，如果以-60dB 作为衡量端口间隔离度好坏标准的话，两种平衡电路除在射频与中频端口隔离度上有显著区别外，其他一些端口间都具有较好的信号隔离度。而在射频与中频端口之间的隔离度上，单平衡电路这两端口间信号串通干扰比较严重，如从中频端口泄露至射频端口的功率和本身的输出功率基本上等量，而双平衡电路则明显要优越的多。在实际中，单平衡电路这两端口间必须加入低通或带通滤波器，才能消除信号间的串通干扰。

4 结论

表1 单平衡与双平衡电路主要端口隔离度仿真计算结果

利用二极管单平衡与双平衡电路的信号相乘功能，可实现振幅调制与信号混频等功能，同时配合一定的滤波器，即可得到比较理想的有用输出信号。通过对两种电路输出信号性能的对比可知，在相同的条件下，二极管双平衡电路比单平衡电路具有更好的信号输出性能；但另一方面，从电路结构上看，单平衡电路更简单些，同时在二极管元件选择及电路设计上也更容易实现参数匹配。因此在实际中，需根据具体的应用需要进行选择。