基于偏最小二乘回归的空气质量数据校准研究
丁学利,任 鹏
(阜阳职业技术学院,安徽 阜阳 236031)
0 引言
空气污染对生态环境和人类健康危害巨大,所以对空气质量进行监测必不可少。目前国家通过监测控制站点(国控点)对PM2.5、PM10、CO、NO2、SO2、O(3“两尘四气”)的浓度进行实时监测[1],虽然数据较为准确,但因布控点较少,且数据发布延迟较长、投资较大,无法对空气质量进行实时监测和预报。通常做法是在国控点近邻自建一些监测控制站点(自建点),利用微型空气质量检测仪对某一地区空气质量进行实时网格化监控,并同时监测温度、风速、气压、湿度、降水量等气象参数[1,2]。由于所使用的电化学气体传感器在长时间使用后会产生一定的零点漂移和量程漂移,非常规气态污染物(气)浓度变化对传感器也存在交叉干扰,以及天气因素对传感器的影响,在自建点上,同一时间微型空气质量检测仪所采集的数据与该国控点的数据值存在一定的差异。因此,需要利用国控点每小时的数据对国控点近邻的自建点数据进行校准。
在空气质量数据的校准方面,可通过建立最小二乘拟合或多元线性回归模型等[3-9]方法进行校准。但由于空气质量数据的校准影响因素较多,且各因素具有较强的非线性,各因素之间存在较强的相关性,普通的线性回归模型很难对数据进行校准。因此,本文考虑建立偏最小二乘回归(PLSR)模型对空气质量数据进行校准。
1 PLSR建模步骤[10-13]
设有n个样本点,矩阵表示含有p个自变量,矩阵表示含有q个因变量,PLSR具体步骤如下:
Step 1:将X和Y分别进行标准化处理。

Step 2:计算第1 对成分t1和u1。记E0的第1 个成分t1,F0的第1 个成分u1。为使t1和u1的相关程度达到最大,需使如下的内积θ1达到最大。

w1可由矩阵计算其最大特征值对应的特征向量得到,v1可通过计算得到。计算出w1和v1,即可得到第1对成分:

Step 3:分别建立E0和F0对t1的回归方程。

其中E1和F1为残差矩阵,回归系数向量α1和β1如下:

Step 4:用E1和F1分别替代E0和F0,重复上述步骤。若F1中元素近似为0,则表明第1 个成分得到的回归模型精度已达到要求,可终止成分的抽取;否则,用E1和F1分别替代E0和F0,重复上述步骤,即可得第2对成分t2=E1w2,u2=F1v2。则有

Step 5:若E0的 秩 是r,则 存 在r个 成 分t1,t2,…,tr,于是有


Step 6:交叉有效性检验[11]。
PLSR 方程一般不需要使用全部的成分t1,t2,…,tr进行回归建模,而是通过截取前h个成分(h<r),即可得到一个回归效果较为理想的模型。提取h个成分的交叉有效性检验定义如下:

每一次提取成分结束前,都利用(9)式进行检验。当第h步时,Q2h<0.0975,则停止提取成分;否则继续提取成分直到达到精度要求为止。
(9)式中p(h)为预测误差的平方和如下:

其中
(9)式中Ss(h)的表达式如下:

2 空气质量校准效果的辅助计算
2.1 样本异常值的检验[10,14]
样本中异常点的存在会导致统计规律产生较大波动,从而使回归线发生较大偏离。第i个样本点对第h个成分th的贡献率定义为:




2.2 校准误差分析[12,13]
为检验校准结果的好坏,需用多个评价指标对校准效果进行整体性的综合评价和衡量。本文应用如下评价指标对校准效果进行评价。
(1)校准前平方和误差


n
(2)校准前均方误差

(3)校准前平均绝对误差

校准后平均绝对误差


(4)校准结果改善百分比物浓度,ŷij为污染物浓度校准值(j=1,2,…,6)。
其中xij为自建点污染物浓度,yij为国控点污染
3 基于PLSR空气质量数据的校准
3.1 数据来源与提取
本文采用2019 年全国大学生数学建模竞赛D题[1]空气质量数据。利用Access 数据库软件提取自建点符合条件的数据,然后将整点附近间隔在5分钟内的自建点数据进行平均得到与国控点整点匹配的数据。删除不能匹配的数据之后,共提取4048 条数据,如表1(展示部分数据)所示。表1 中,x1、x2、x3、x4、x5、x6、x7、x8、x9、x10和x11分别表示自建点的PM2.5 浓度、PM10 浓度、CO 浓度、NO2浓度、SO2浓度、O3浓度、风速、压强、降水量、温度、湿度;y1、y2、y3、y4、y5和y6分 别 表 示 国 控 点 的PM2.5 浓 度、PM10浓度、CO浓度、NO2浓度、SO2浓度、O3浓度。
3.2 相关性分析
表2是对自建点的11个自变量和国控点的6个因变量进行相关性分析的结果。从表2可知,x1与x2、y1、y2;x2与y1;y1与y2之间具有较强的相关性(大于0.7),而x8与x10的相关系数是-0.85,说明具有较强的负相关,其他因素之间的相关系数均小于0.7。根据各因素之间的相关性,可考虑以自建点的11个变量为自变量,国控点的6个变量为因变量建立PLSR模型。
3.3 异常数据处理
以x1-x11为自变量,y1-y6为因变量作PLSR,提取两个主成分t1和t2。根据(15)式,可在t1-t2平面上画出散点图和椭圆图,如图1。图1中的椭圆之外有318个点,则认为这些点是异常点,将其提取并进行剔除。
3.4 校准结果分析
利用清洗后的数据重新进行PLSR 建模。首先做交叉有效性检验(见表3)。当h=4 时,因此,只要抽取前4 个主成分即可建立合理的PLSR 方程,其回归方程的系数如表4所示。此回归方程即可作为自建点空气质量的校准方程。
为了对表4 构成的6 个回归方程进行精度分析,分别作了如下分析。
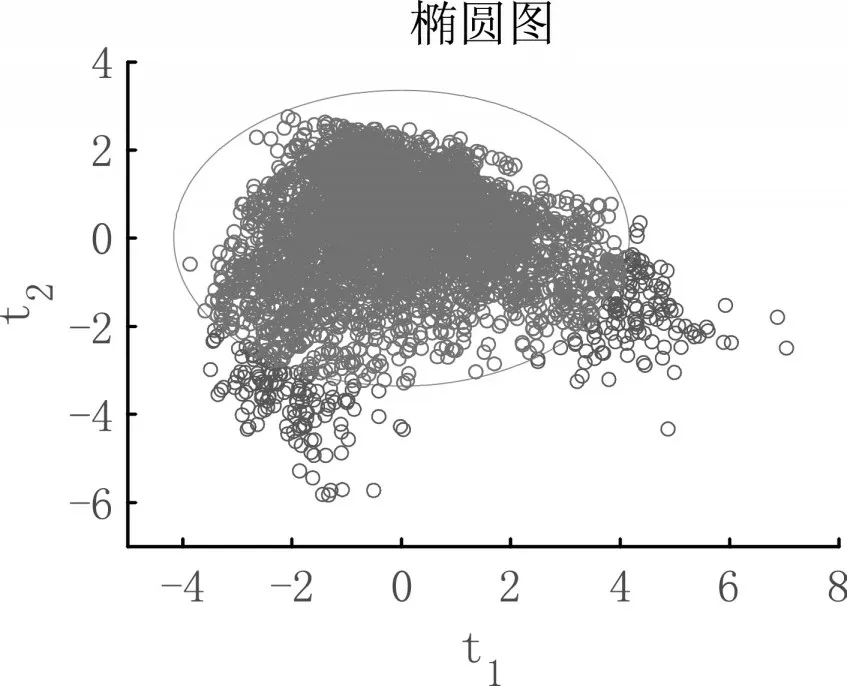
图1 t1-t2成分椭圆图

表1 自建点与国控点匹配数据

表2 相关系数矩阵
(1)自建点6 种空气质量数据的预测。图2 是以自建点的校准值为横坐标,国控点的实际值为纵坐标,对6 种空气质量数据的样本点作预测图。在预测图2上,若所有的点都能在直线y=x左右均匀分布,则回归方程的拟合效果是满意的,说明校准值与实际值差异很小。在图2中,除SO2的预测效果较差外,其余空气质量数据均能在直线y=x左右均匀分布,说明校准效果较满意。

表3 交叉检验值
(2)6 种空气质量数据的校准值与实际值的时序图,如图3。除SO2的前半部分以及O3的后半部分的校准值与国控点数据吻合的较差外,其他数据的校准值都能与国控点数据较好地重合,表明利用PLSR取得了较好的校准效果。

表4 PLSR方程系数
(3)对6 种空气质量数据校准前后进行误差分析。由表5 知,各个校准误差指标均低于校准之前的误差指标。另外从整体校准改善的百分比看,PM10 校准改善的最好,达到了63.89%;SO2校准改善的效果最差,只有16.02%。从整体上看自建点的空气质量数据均得到不同程度的校准,说明基于PLSR模型的校准方法取得了较好的效果。

图2 自建点6种空气质量数据的预测图

图3 6种空气质量数据的校准值与国控点实际值的时序图
4 结语
从数据校准结果知,自建点空气质量数据校准后的误差都有明显降低。同时发现PLSR 模型对具有多重共线性的自变量(如PM2.5 和PM10)校准效果明显。但并非对自建点所有的污染物浓度都能有效地校准,如对SO2校准改善的效果最差,其次是O3,这可能受污染物浓度变化对传感器的交叉干扰,以及气象因素剧烈变化对传感器的影响。今后可进一步尝试寻找SO2数据校准的关键影响因素,建立符合数据特点的非线性回归模型。

表5 6种空气质量数据校准前后的误差对比

