Centrifuge model test and numerical interpretation of seismic responses of a partially submerged deposit slope

Zhiliang Sun ,Lingwei Kong ,Aiguo Guo ,Mohammad Alam

a State Key Laboratory of Geomechanics and Geotechnical Engineering,Institute of Rock and Soil Mechanics,Chinese Academy of Sciences,Wuhan,430071,China

b University of Chinese Academy of Sciences,Beijing,100049,China

Keywords:Centrifuge model test Acceleration responses Excess pore pressure Deposit slope

A B S T R A C T Partially submerged deposit slopes are often encountered in practical engineering applications.However,studies on evaluating their stability under seismic loading are still rare.In order to understand the seismic behavior of partially submerged deposit slopes,centrifuge shaking table model tests(50g)were employed.The responses of horizontal accelerations,accumulated excess pore pressures,deformation mode,and failure mode of the partially submerged deposit slope model were analyzed.In dynamic centrifuge model tests,EQ5 shaking event was applied numerically.The results indicated that in the saturated zone of the deposit slope,liquefaction did not occur,and the measured horizontal accelerations near the water table were amplified as a layer-magnification effect. It was also shown that the liquefaction-resistance of the deposit slope increased under multiple sequential ground motions,and the deformation depth of the deposit slope induced by earthquake increased gradually with increasing dynamic load amplitude.Except for the excessive crest settlement generated by strong shaking,an additional vertical permanent displacement was initiated at the slope crest due to the dissipation of excess pore pressure under seismic loading.The result of particle image velocimetry(PIV)analysis showed that an obvious internal arc-slip was generated around the water table of the partially submerged deposit slope under seismic loading.

1. Introduction

It is widely acknowledged that slope instability is generally the result of a combination of multiple factors.Hydraulic and seismic dynamics are the two major factors that can cause slope instability.Field investigations after Wenchuan and Lushan earthquakes(Yin et al.,2009;Ding and Miao,2015;Xu et al.,2015)showed that a groundwater-rich slope was seriously damaged due to the earthquake.Nevertheless,the failure mode,instability mechanism,and damage to the sliding area of the slopes rich in water were significantly different from those of slopes with less groundwater.The dynamic responses and failure modes of slopes under hydraulic and seismic coupled loading are the challenging issues that need to be solved.

In the southwestern China, deposit slopes are commonly observed.Over the past years,it was generally believed that the permeability coefficient of coarse-grained geomaterials is considerably large and subsequently the deposits were regarded as a non-liquefiable soil(Lin et al.,2004;Fioravante et al.,2012;Chang et al.,2014;Huang and Zhu,2017).Excess pore pressures in deposits were considered not to reach the values required for liquefaction under earthquake excitations; however, site investigations after Wenchuan earthquake illustrated that the particle size of liquefied gravel soils varied greatly, with an average particle size of 0.15-33.4 mm.In some liquefaction sites,the diameter of the gravel varied from 30 mm to 100 mm(e.g.cobbles),and the maximum diameter thereof reached 150 mm(Cao et al.,2011,2013).This indicates that coarse-grained soil could also be liquefied in some extreme cases, which is beyond our existing understanding and further investigation is needed.

Fig.1.Layout of the model slope and instrumentation in the model scale(unit:mm).

Earthquake-induced slopes have been investigated extensively over the past few decades.Using centrifuge shaking table tests,Kulasingam et al.(2004)and Malvick et al.(2006,2008)studied the diffusion process of excess pore pressure in a sand slope with embedded silt layers.Experimental results and theoretical analyses showed that the change in shear strength of granular material induced by high excess pore pressures is not only related to the initial material properties(e.g.pre-shaking density,and penetration resistance),but also dependent on sand layer thickness,slope angle, and low-permeability properties of embedded layers.Taboada-Urtuzuastegui et al.(2002)studied the seismic behavior of liquefiable soil slopes by centrifuge model test,and found that the dilatancy of sand has an important indicator on the lateral permanent displacements of soil slopes. Boulanger et al. (2014)investigated the liquefaction-induced deformations of geotechnical structures affected by many uncertain factors through physical model tests and numerical simulations,and then discussed the limitations of current investigations to consider void redistribution in nonlinear deformation analysis.Yoshikawa et al.(2016)numerically studied the seismic responses of unsaturated dams located on a clay foundation under different water levels.It was found that the higher the groundwater level,the greater the permanent settlements induced by earthquake.Wang et al.(2013)used dynamic centrifuge model tests and three-dimensional (3D) numerical simulations to study the seismic response of dike on liquefiable soils.The distribution and variation of deformation,acceleration,excess pore water pressure and dilatancy in dam and liquefiable soil foundation were analyzed.Baker et al.(2005)calculated the safety factor of non-cohesive soil slopes with different immersion depths,and it was observed that when the water level is close to the mid-depth of the slope,the safety factor of the slope is reduced.It showed that excess pore pressure caused by earthquake is one of the major factors with respect to slope stability.Increasing pore pressures means that the effective stress on the soil decreases,which can mobilize the shear resistance of soil and affect the slope stability consequently.Most of currently used approaches mainly focus on the liquefaction characteristics of saturated sand slopes under seismic loading. The topics associated with seismicinstability of submerged slopes mostly focus on post-disaster investigations and numerical simulations in case of landslides.However,the whole process of the seismic responses of a submerged slope under in situ stress state is rarely reported.

Table 1 Particle size distribution and physico-mechanical parameters of the tested deposit.

Physical model testing is a powerful tool used for understanding the stability of slopes under seismic loading (Taboada-Urtuzuastegui et al.,2002;Lin and Wang,2006;Yu et al.,2008;Wang and Lin,2011;Conlee et al.,2012;Abdoun et al.,2013;Al-Defae et al.,2013;Fan et al.,2017;Zhang et al.,2017).Since the model size of large-scale shaking table test could be generally large,it is possible to consider the effect of particle size on the deposit with large particle size.However,the stress-strain similarity ratio in a 1g test will not be satisfied.The testing result is not convincing in a quantitative analysis manner in view of acceleration amplification effect and deformation mode.Compared with shaking table tests(Lin and Wang,2006;Wang and Lin,2011;Ma et al.,2019),a centrifuge shaking table test could better yield the similarity relationship between stress and strain,and provide actual stress levels of prototype slope subjected to earthquake excitations,as the gravitational field of prototype can be represented by centrifuge test through high-speed rotation of centrifuge to form a stable centripetal acceleration.

To understand the dynamic responses of partially submerged deposit slopes under seismic loading,centrifuge model tests were conducted considering the coupling effects of seismic loading and water.Meanwhile,dynamic numerical simulations were performed using finite difference code FLAC(Itasca,2011)to reproduce the slope response to ground motions.Next,the numerical results were compared with the testing results to validate the reasonableness of the simulations.The acceleration responses and changes in excess pore pressures of the partially submerged deposit slope under different excitation intensities were analyzed.Finally,the deformation feature and failure mechanism of the partially submerged deposit slope subjected to earthquakes were discussed.

2. Centrifuge test programme

2.1. Centrifuge shaking table

Centrifuge tests were conducted using the ZJU-400 centrifuge equipment developed in Zhejiang University, China. It has aneffective radius of 4.5 m and a capacity of 400 g-t.The sizes of the shaking table used in the tests are 800 mm in length and 600 mm in width.Its loading capacity is 0.5 t.The earthquake waves are applied to the model in horizontal direction through the shaking table,which has a maximum acceleration capacity of 40g(Zhou et al.,2010,2018;Chen et al.,2017).The shaking table is operated in the frequency range of 0.2-200 Hz.The advantage of the centrifuge is that it allows the reduced scale models to realize fullscale stress conditions.

Table 2 Selected centrifuge scaling laws.

Fig.2.Schematic diagram of saturation system.

A rectangular rigid model box with internal dimensions of 770 mm×400 mm×530 mm(length×width×height,L×W×H)was used in these centrifuge tests.The Plexiglass®observation window of the model box has the dimensions of 650 mm×330 mm(L×W).The control points used in particle image velocimetry(PIV)analysis(White,2002;White et al.,2003;Saiyar et al.,2011)were marked on the observation window.A layer of 25 mm soft plate was sandwiched between the deposit and each end-wall (see Fig.1). The interior of the plate is filled with plasticine.This set-up was used to reduce the reflected waves at the boundaries in the shaking direction.It is verified that the soft plasticine plate is effective in reducing the energy reflected from the container walls(Heron et al.,2015).

2.2. Model design and construction

The tested deposit has the maximum and minimum dry densities ofρdmax=2.102 g/cm3andρdmin=1.466 g/cm3,respectively.Its grain size distribution and physical parameters are tabulated in Table 1.The slope model is made of deposit with an initial dry density(ρd)of 1.81 g/cm3,an initial void ratio of 0.452,and a relative density(Dr)of 0.628.The permeability coefficient of the tested soil sample,i.e.3.93×10-4cm/s,is obtained at ρd=1.81 g/cm3(Dr=0.628).

Fig.3.Input El Centro waves(measured by BA-0).

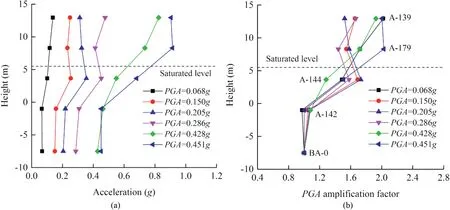
Fig.4.Horizontal acceleration responses along the slope surface:(a)Maximum acceleration vs.height;and(b)PGA amplification factor vs.height.

The scale factor of the centrifuge model is 50(prototype scale/model scale=50),and some of the scaling laws adopted in this study are listed in Table 2.The slope tested in the model has a slope angle β=40°(β ≈38°after consolidation under 50g centripetal acceleration)at 1:50 scale.The slope height is 14.5 m in the prototype(h ≈14 m after consolidation under 50g centripetal acceleration).The most challenging issue for any seismic centrifuge test on saturated soil structure is to address different time scales(Dewoolkar et al.,1999;Ng et al.,2004;Zhou et al.,2018;Tokimatsu et al.,2019).In the centrifuge tests,the scale factor for diffusion or consolidation time is 1/N2(where N is the acceleration).On the other hand,the inertial or dynamic time is scaled by a factor of 1/N(see Table 2).Silicone oil with a density of 0.96 g/cm3is used in these centrifuge tests as a substitute pore fluid.The viscosity of the silicone oil is 50 cS(1 cS=1×10-6m2/s),which is 50 times that of pure water under the same scenario.

In preparation of slope model,the soil deposits with a dry density of ρd=1.81 g/cm3were compacted into the model box using the controlled-volume method (Lin and Wang, 2006)(ρd≈1.83 g/cm3after consolidation under 50g centripetal acceleration).The slope model was constructed in nine layers,with each layer of 50 mm in thickness.The required soil weight for each layer was calculated based on the dry density.In order to reduce the separation between the coarse and fine particles and to ensure the uniformity of the model,the soil material was evenly spread in the model box with a spoon.After each layer of soil material was paved,the soil material was gently leveled with a soft brush,and the leveling of each layer of soil was ensured by the inspection of level gauge.It should be ensured that the same compaction energy was used to compact each soil layer,and the number of compaction per unit area of compaction slab was consistent.Finally,each layer of soil was compacted to the design height and sensors were embedded to the target locations.A soft brush was used to remove any extra soil from top to bottom until the design contour of the model slope was reached.Fig.1 shows the layout of monitoring points.Accelerations were measured using accelerometers at positions marked with a rectangle and labeled “A”. Pore pressures were measured using pore water pressure transducers at positions marked with a dot and labeled“PP”.Vertical displacements of the slope crest along the centerline of the model were measured by linear variable differential transformers LVDT-1 and LVDT-2.

Fig.5.Horizontal acceleration responses along the slope height:(a)Maximum acceleration vs.height;and(b)PGA amplification factor vs.height.

Fig.6.Pore pressure build-up and dissipation during shaking events:(a)PGA=0.15g,(b)PGA=0.205g,(c)PGA=0.286g,(d)PGA=0.428g,and(e)PGA=0.451g.

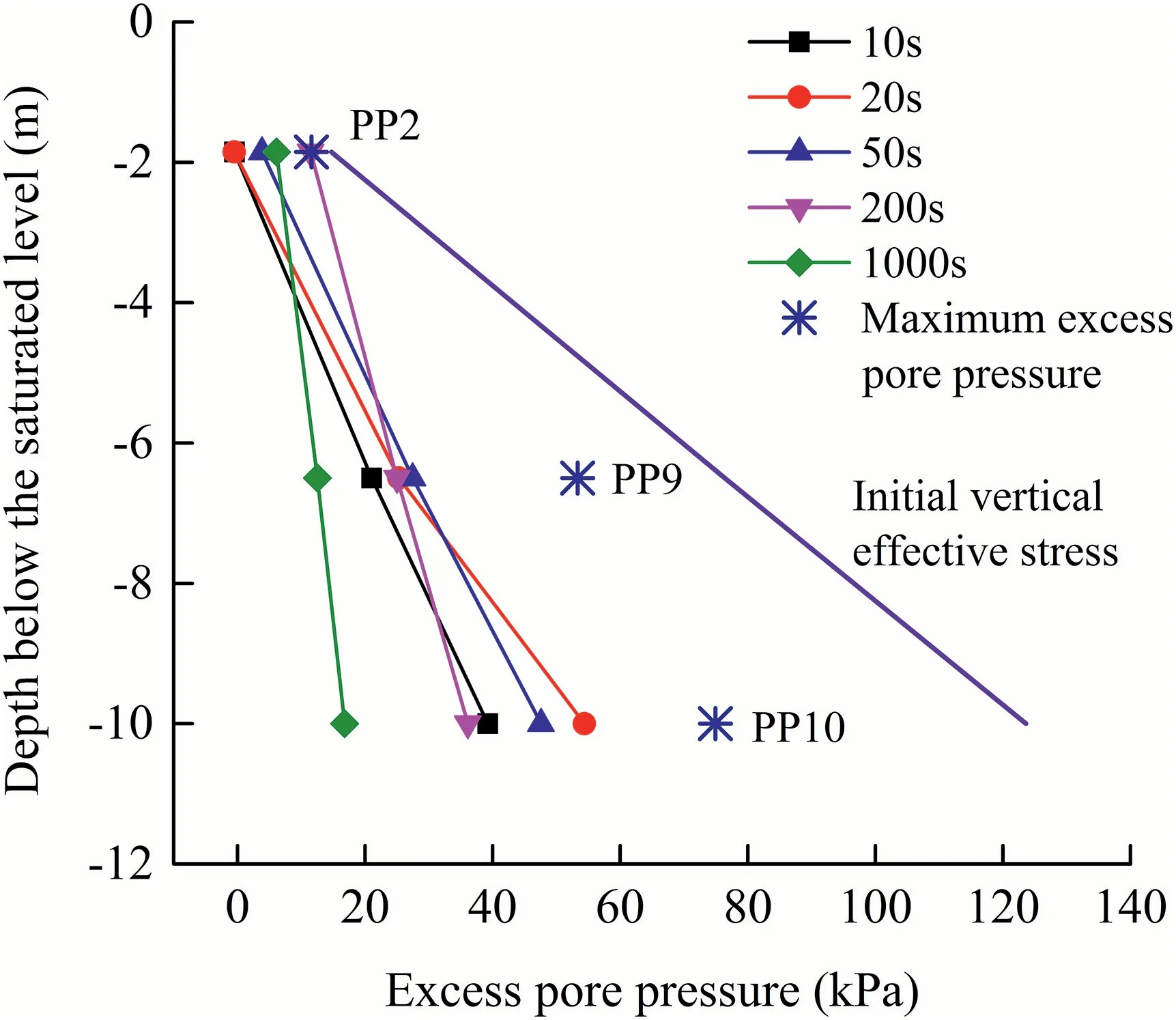
Fig.7.Excess pore pressure profiles(EQ5,PGA=0.428g).

When the soil model was completed,it was saturated using 50 cS silicone oil as a substitute pore fluid.Saturation was conducted in an air-tight vacuum chamber.The schematic diagram of saturation system is shown in Fig.2.The saturated procedure is primarily divided into three steps:

(1)Calculate the required volume of methyl silicone oil according to the design height,and then put it into the oil storage tank.

(2)Open the vacuum pump to pump out the vacuum saturation tank and the oil storage tank,control the height of the oil storage tank,open the valve,and let the silicone oil flow into the model box by its own weight.

(3)A week later,when the silicone oil has reached the design level,saturation is achieved.

2.3. Test procedure

During the test,the input ground motions were adjusted from the standard El Centro wave.The seismic loading sequence was set by changing the wave amplitude as follows: 2.5g→5g→10g→15g→20g→22.5g(corresponding to the prototype of 0.05g→0.1g→0.2g→0.3g→0.4g→0.45g).Correspondingly,the six shaking events were named EQ1→EQ2→EQ3→EQ4→EQ5→EQ6.After shaking time period of 50 s for each shaking event,the model was held for 15 min under centripetal acceleration of 50g(nearly 26 d in prototype),in order to ensure that the excess pore pressure was completely dissipated.The actual input ground accelerations were recorded by the accelerometer BA-0,as illustrated in Fig.3.It should be pointed out that,for clarity purpose,only the 50 s shaking period of each event is shown in Fig.3.

The acquisition frequency in the static period is 1 Hz and that in the dynamic period is 5000 Hz when collecting the test data.During the testing,high-resolution images of slope lateral view were obtained at 6 s interval using a camera fixed on a hanging basket.The images were post-processed using the PIV method,and the deformation characteristics on the side of the slope before and after each seismic loading event were analyzed.

3. Testing results and analyses

3.1. Horizontal acceleration response

The acceleration responses were recorded by the acceleration transducers installed in the slope model(see Fig.1).Here,the peak ground acceleration(PGA)is an amplification factor defined as the maximum acceleration measured by the accelerometers in the slope model at a given depth divided by the maximum acceleration measured by the sensor located at the base of the shaking table(BA-0).

The distributions of horizontal accelerations along the slope surface were obtained by the sensors BA-0,A-142,A-144,A-179 and A-139(Fig.4),whilst those along the slope height were obtained by the sensors BA-0,A-4,A-7,A-1079 and A-139(A-1077 failed during the tests),as shown in Fig.5.In Figs.4 and 5,the elevation of slope toe is set as the zero point of height.It can be observed that in the six stages of earthquake excitations,the PGA amplification factors obtained from accelerometers located both near the slope surface and in the slope body generally increased along the slope height.For example,the maximum PGA amplification factor at the slope crest in EQ1 is around 2 according to Figs.4b and 5b,suggesting an obvious elevation amplification effect.Meanwhile,the accelerations measured by the sensors A-1079 and A-144,which were located near the saturated liquid level,were amplified.The reason could be that the soils situated above and below the saturated water level exhibited certain differences in physical and mechanical properties.Reflected waves will be generated in the saturated level when the seismic wave propagates from bottom to the slope crest,which reveals the layer amplification effect.In addition,the effective stress at the measuring points can be reduced by the positive excess pore pressure in the saturated part of the slope under seismic excitation,and the stiffness modulus of the deposit is then decreased as the effective stress decreases,which may also magnify the acceleration responses to some extent.

It also can be seen from Figs.4 and 5 that the measured accelerations near the slope crest increased in the last two shaking events(EQ5 and EQ6)compared with previous shaking events.It is likely that the deposit at the slope crest was loosened and/or began to fail under such strong seismic excitations,which amplified the acceleration measured by accelerometer A-139.In view of the loading history,the horizontal PGA amplification factor calculated from the data recorded by sensor A-139 decreased as the input ground motion amplitude increased,and it reached a threshold value in EQ3 and then increased(Figs.4b and 5b).This behavior is different from the dynamic response of a loess-mudstone slope as reported by Zhang et al.(2017).As small earthquake loads(EQ1,EQ2,and EQ3)were applied initially,the loose compacted soil particles started to move,resulting in an increase in soil density.When the input acceleration amplitude reached 0.286g in EQ4 and continued to increase to 0.451g in the last shaking event(EQ6),the upper part of the deposit slope dilated and became loose,or even failed.The amplification of acceleration was increased near the slope crest due to the loosening deposit material.This may explain that the horizontal accelerations first decreased and then increased with increasing intensity of input seismic waves.

3.2. Accumulation and dissipation of excess pore pressure

Fig.6 shows the time histories of excess pore pressure at different depths in EQ2,EQ3,EQ4,EQ5 and EQ6.As the increase of excess pore pressure in shaking event EQ1 was not obvious,it was not included herein.The shadow on each graph in Fig.6 details the 50 s shaking period and is re-plotted at a larger scale on the righthand side of each graph for details.When the excess pore pressure increases significantly in the shaking period(see Fig.6),we can observe that the maximum value of excess pore pressure increases with increasing distance from the saturated liquid level(PP2 ＜PP1＜PP9 ＜PP10).

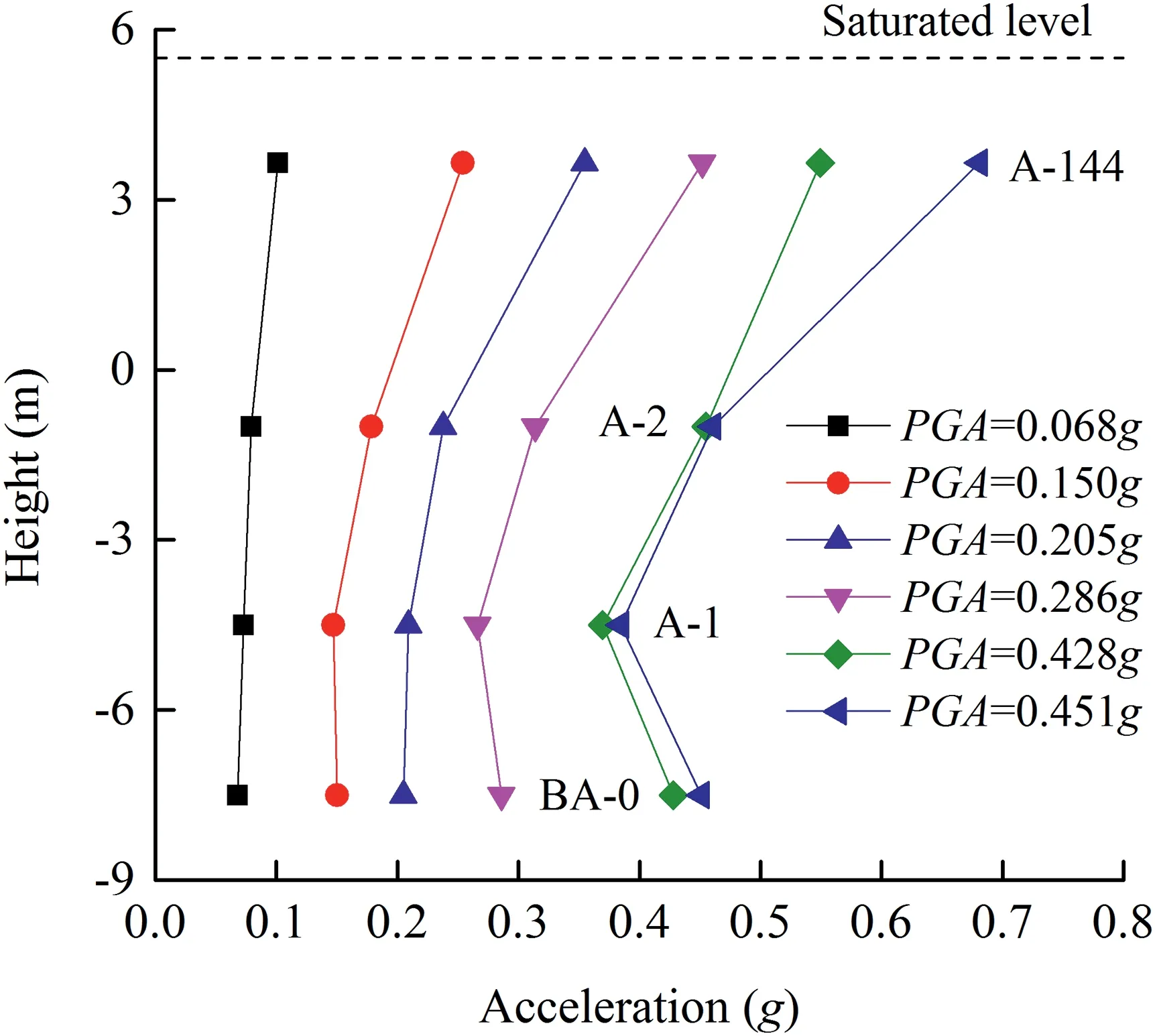
Fig.8.Distributions of the maximum horizontal accelerations along the related positions of pore water pressure transducers(BA-0,A-1,A-2 and A-144).

It is worth noting that the trend of excess pore pressure timehistory curve measured by transducer PP2 is different from those measured by other pore pressure transducers.This may be due to the fact that the deposit volume expanded when the grain skeleton was sheared under seismic load as the effective stress near PP2 was relatively low.The greater the ground motion,the more obvious the dilatancy effect(see the negative excess pore pressure generated in the 50 s shaking period illustrated in Fig.6d and e).After the shaking stage,the pore pressure continued to rise for a short time period at PP2,mainly due to the volume-contraction in unloading stress path of granular geomaterials.Then the excess pore pressure gradually dissipated as the granular structure of the deposit slope was stable,as observed at pore pressure transducers PP1,PP9 and PP10.

The excess pore pressure ratio is defined as ru=Δu/σiv,where Δu is the increment of excess pore pressure and σivis the initial vertical effective stress recorded at the pore pressure transducer location.Taking the EQ5 event as an example,Fig.7 shows the excess pore pressure profiles in the saturated part of the deposit slope at different time periods(t=10 s,20 s,50 s,200 s and 1000 s).Moreover,Fig.7 shows the maximum pore pressures and the distribution of initial vertical effective stress,which can be used to assess whether liquefaction conditions have been reached at a given depth:liquefaction did not occur in the deposit in EQ5 as all the maximum points were located in the left-hand side of the initial vertical effective stress line.

Table 3 summarizes the data of maximum excess pore pressure and maximum excess pore pressure ratio.From Table 3,it can be found that with increasing depth from the saturated surface,the excess pore pressure ratio shows a decreasing trend.For example,in shaking event EQ4(PGA=0.286g),the corresponding excess pore pressure ratio of PP2 reaches a peak value of 0.55,greater than those in PP9 and PP10 that have excess pore pressure ratios of 0.41 and 0.37,respectively.

Fig.9.Crest settlement during the shaking period.

In addition, with the increase of the input seismic wave magnitude(from EQ2 to EQ6),the excess pore pressure ratio at PP9 exceeds that at PP2.The excess pore pressure ratio at PP10 also gradually approaches that at PP2,indicating that the disturbed depth of the deposit slope is gradually increased with increasing ground motion.

It is generallyconsidered that liquefaction occurs when the excess pore pressure ratio reaches 1.In these tests,all the maximum excess pore pressure ratios are less than 1,as shown inTable 3.This suggests that no liquefaction occurs at each measuring point in each shaking event.Nevertheless,the accumulated excess pore pressure cannot be ignored.Taking the shaking event EQ5(PGA=0.428g)as an example,the maximum excess pore pressure ratios obtained from PP9 and PP2 are 0.7 and 0.79,respectively.In other words,the effective stresses at PP9 and PP2 were reduced by 70% due to the accumulation of excess pore pressure. Decreasing the effective stresses can effectively decrease the stiffness modulus of the deposits and weaken the soil,and consequently cause slip deformation near the saturated liquid surface of the slope,or even result in slope failure.

As the multi-level seismic loading procedure was applied in the tests,the impact of previous seismic excitations on the pore pressure accumulation in subsequent shaking events needs to be considered.Fig.6d and e shows the time histories of excess pore pressure in events EQ5 and EQ6,respectively.Comparing these two datasets,it is observed that the trend of the two shaking events is similar except for a slight difference in the measured values. While taking the maximum excess pore pressure ratios ru(see Table 3)into consideration,it was noted that the maximum excess pore pressure ratios near the saturated liquid level obtained from PP1 and PP2 in EQ6 are less than those in EQ5.While the maximum pore pressure ratios obtained from PP9 and PP10,which are located at a little farther distance from the saturated liquid level in EQ6,exceeded those obtained in EQ5,respectively,and the maximum excess pore pressure ratios still increased when the input acceleration was increased.This is likely because when the saturated pressure ratios of the deposit soil exceeded a threshold value,the interparticle structure of the soil began to be adjusted, thereby enhancing its ability to resist liquefaction.

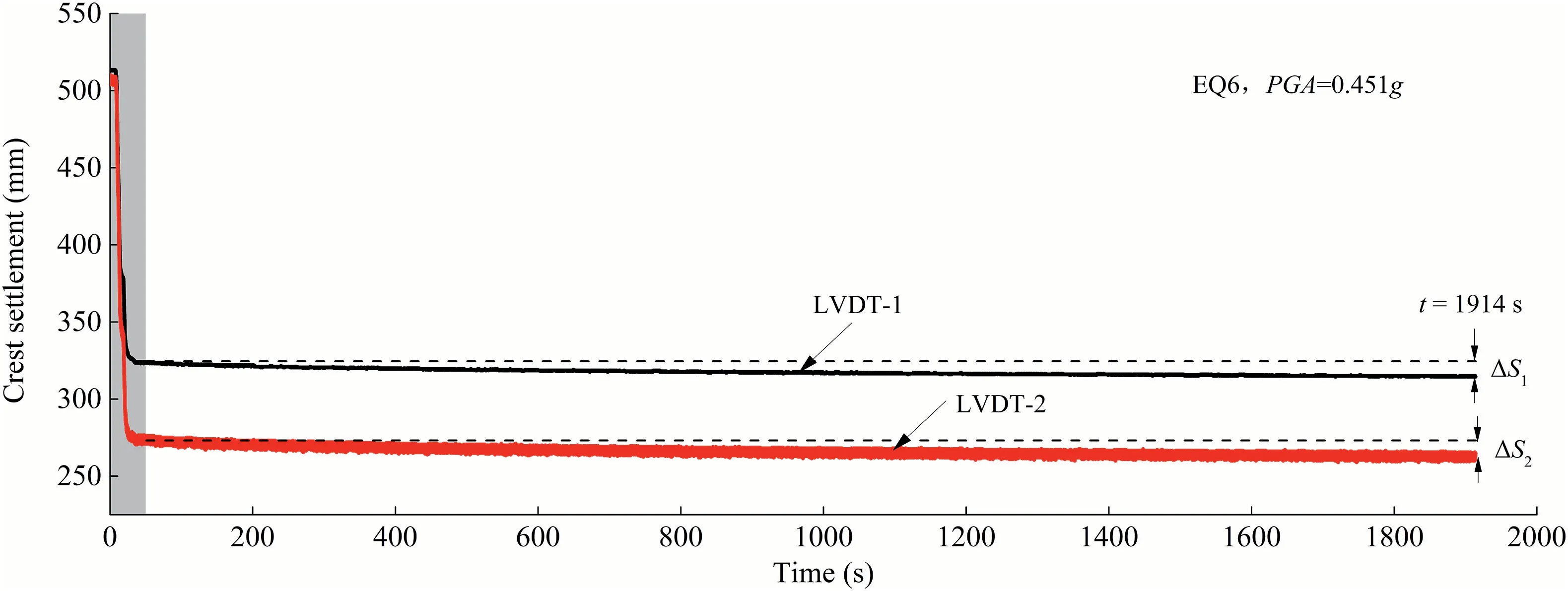
Fig.10.Time-histories of crest settlement(PGA=0.451g).

Fig.11.Displacement vectors of slope during the earthquake loading at model scale(EQ5,PGA=0.428g).

The distributions of horizontal accelerations near the pore pressure transducers along the slope height were obtained by sensors BA-0,A-1,A-2 and A-144,as shown in Fig.8.Amplifications increased nonlinearly and reached maximum values near the saturated water level.The maximum excess pore pressure ratios in Table 3 were generally consistent with the distributions of accelerations at the corresponding positions in Fig.8,that is,within a non-liquefied state, the amplified acceleration responses can effectively increase the excess pore pressure ratios in saturated deposits.Meanwhile,the corresponding effective stresses were decreased by the excess pore pressure,given the amplification of accelerations.

It should be pointed out that,after strong ground motions(EQ5 and EQ6),the model slope will deform and the saturated liquid surface will rise slightly.For example,in EQ5(PGA=0.428g),the increase of static pore pressure ΔP is about 1.4 kPa(see Fig.6d).As the pore pressure change is small,the influences of ΔP on the maximum excess pore pressures and the maximum excess pore pressure ratios can then be ignored.

3.3. Displacement and deformation analyses

The permanent slope crest settlements across the six shaking events measured in the centrifuge tests are shown in Fig.9.Only the data with respect to the 50 s shaking stage in each event are depicted.These do not include the settlements generated during the excess pore pressure dissipation stage(t ＞50 s)as there are significant changes between 200 s and 250 s in the settlement time histories,as illustrated in Fig.9.Taking the event EQ6 as an example(see Fig.10),the difference of settlements ΔS1measured by LVDT-1 is 10 mm and ΔS2measured by LVDT-2 is 8.6 mm when the excess pore pressure is dissipated from 50 s to about 1900 s.This indicates that the crest settlements are still increasing in the stage when the excess pore pressure is dissipated.

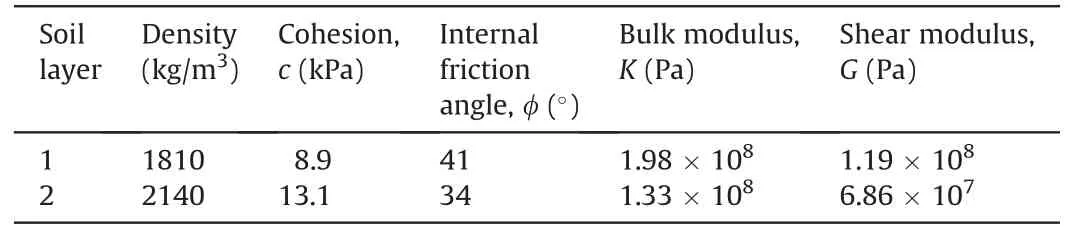
Table 4 The material parameters used in the numerical model.

Under multi-excitation,the crest displacements were gradually accumulated,as shown in Fig.9.It can be seen that,in the first two stages(EQ1 and EQ2),the changes of settlements are not significant.When the maximum input acceleration increases to 0.205g(EQ3),the permanent displacements occur,resulting in significant settlements in EQ4(PGA=0.286g).Finally,significant permanent displacements are generated at the slope crest in events EQ5(PGA=0.428g)and EQ6(PGA=0.451g).This shows that when the input acceleration reaches the critical value,the slope will be permanently deformed,and the larger the input PGA,the greater the permanent deformation.

The settlement measured by LVDT-2 in EQ6 is 232.1 mm,which is smaller than the measured value of 302.2 mm in EQ5,indicating that the previous ground motions can reduce crest settlements in subsequent earthquakes.After all of the six shaking events,the cumulative settlements measured by LVDT-1 and LVDT-2 are 598.1 mm and 690.1 mm,respectively.The angular distortion θdwas calculated by the vertical settlement difference between the two LVDTs as shown in Fig.1,divided by the horizontal distance between them,that is,θd=(ΔD2-ΔD1)/L(Al-Defae and Knappett,2014).The horizontal distance between the two LVDTs is 3 m,thus the angular distortion θdof the deposit slope after all the six shaking events is 3.07% .

The deformation of the vertical slope cross-section was captured by the PIV analysis programme GeoPIV written by White et al.(2003).Silicone oil is applied on both sides of the model box to reduce the friction between the sidewalls of the model box and the soil.Fig.11 shows a plot of the displacement vectors based on the PIV analysis in EQ5.The length of the vector arrow represents the amount of displacement and the arrows have been magnified fivefold for ease of observation.It can be found that the partially submerged deposit slope tends to have a curved slip surface inside the slope near the saturated surface under strong ground motion.

4. Numerical analysis:shaking event EQ5

4.1. Numerical modeling

Fig.12.The meshing of numerical model.

Fig.13.Comparison of acceleration responses between the dynamic centrifuge model test results and the numerical simulations(EQ5,PGA=0.428g):(a)Maximum acceleration distributions along the slope surface;(b)Maximum acceleration distributions along the slope height;and(c)Maximum acceleration distributions along the locations of pore pressure transducers.

To interpret the testing results and verify the effectiveness of the centrifuge model test results,numerical simulations were conducted on the same prototype used in the centrifuge model tests.The explicit finite difference code FLAC was used to simulate the typical shaking event EQ5.In EQ5,significant excess pore pressure accumulation and large crest settlements occurred.As shown in Fig.12,the dimensions of the slope were based on those of the prototype with extensions at the left and right boundaries to simulate semi-infinite boundary conditions. Four steps were adopted for numerical modeling in the present study:

(1)Adjust the input motion for accurate wave propagation,and generate appropriate model grid.

(2)Calculate the static equilibrium state,and then apply the dynamic loading conditions.

(3)Perform preliminary undamped simulations to check model conditions and estimate the dominant frequencies of the slope model resonance and the maximum cyclic shear strains.

(4)Fixed boundary, free field boundary and representative damping are adopted for dynamic and seepage coupling analysis.

In FLAC, the Finn-Byrne model (Byrne,1991) was used to describe the pore pressure cumulative effect of the saturated soil under ground motion.The Byrne formulation is proposed as

where Δεvdis the increment of volume strain,εvdis the accumulated volume strain,γ is the cyclic shear strain,and C1and C2are the constants（C1=0.4/C2）.In this method,it is assumed that the dynamic pore pressure generation is related to the plastic volumetric strain increase,which incorporates the Byrne relationship between irrecoverable volume change and cyclic shear strain amplitude into the Mohr-Coulomb constitutive model (Byrne,1991).

In this model,the soils above and below the saturated liquid surface are considered as layers 1 and 2,respectively.The physicomechanical parameters of the soil layers are summarized in Table 4.The initial soil voids ratio e is 0.45 and the measured coefficient of permeability k is 3.93×10-4cm/s(4×10-10m2/(Pa s))for the deposit before compaction. To simulate the strain-dependent behavior of the soil,the hysteretic damping sigmoidal 3 model embedded in FLAC was used(Itasca,2011).The selected parameters(a=1,b=-0.65,and x0=-0.45)according to the resonant column test results were used in the simulation.To eliminate the effect of high-frequency noise on the dynamic response,a 0.2% Rayleigh damping stiffness component corresponding to the 1.44 Hz predominant frequency of the input wave was assigned in the whole model. The Finn-Byrne model parameters were selected as C1=0.49 and C2=0.816.

Fig.14.Comparison of crest settlements between the dynamic centrifuge test results and numerical simulations(EQ5,PGA=0.428g).

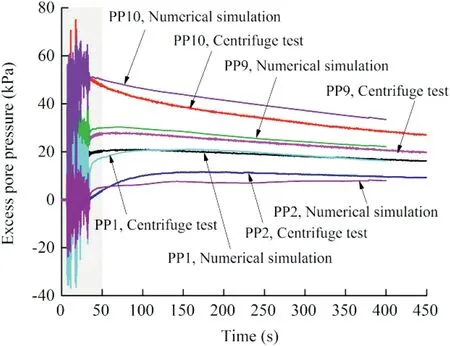
Fig.15.Comparison of excess pore pressure build-up and dissipation between the dynamic centrifuge model test results and numerical simulations(EQ5,PGA=0.428g).

4.2. Comparison between experimental results and numerical simulations

4.2.1. Acceleration response

The comparison of accelerations between the centrifuge model test and numerical simulations of event EQ5 is shown in Fig.13.To analyze the trend of the simulated acceleration responses with different input excitation intensities, the numerical results of events EQ1,EQ2,EQ3,and EQ4 are also depicted in this figure.It is found that the acceleration distributions obtained by the numerical analyses are in good agreement with those from the centrifuge test when the magnitude of input acceleration is relatively small(PGA=0.068g,0.150g,and 0.205g).As the magnitude of input ground motions increased,the discrepancy between the numerical results and the centrifuge test data concerning the accelerations in the upper part of the slope increased.In EQ5,the centrifuge test results and numerical simulations are basically consistent at depths below 5 m,while the deviation is larger near the crest of the slope as the numerical simulation results are smaller than those of centrifuge tests. The reasons could be due to the changes in compactness and mechanical parameters of deposits under continuous multi-stage earthquakes in the centrifuge tests,which were not taken into consideration in the numerical simulations.In general,the numerical simulation herein will underestimate the acceleration amplification effect at the upper part of the slope when subjected to higher-intensity ground motions,while the dynamic numerical analysis data are consistent with those from centrifuge shaking table tests when the input acceleration is moderate.

4.2.2. Crest settlements

Fig.14 shows the comparison of crest settlements between the numerical simulations and centrifuge test results.It can be found that the numerical simulation provides a good trend prediction,allowing for some over-prediction of crest settlements.The measurement of crest settlements in the centrifuge model test in EQ5 could be reduced by previous shaking events,and unfortunately,this factor was not considered in the numerical simulation.In addition,the soils in different regions of the slope model have different stress states and different stiffness moduli(bulk modulus K and shear modulus G);while in the numerical simulation,the stiffness modulus of the deposit is assumed to have the same value.The above two factors could increase the discrepancy between the numerical simulations and centrifuge test results.

4.2.3. Excess pore pressure

As shown in Fig.15,the excess pore pressure vs.time plots obtained numerically are in good agreement with those from the centrifuge test results for event EQ5,indicating that the pore pressure cumulative model adopted in the present paper is reasonable.

Fig.16.Shear strain increment of slope in static and dynamic conditions:(a)Static condition,FS=1.514;and(b)EQ5,PGA=0.428g(t=50 s).

Fig.17.Failure mode of a partially submerged cohesionless slope under static conditions(Baker et al.,2005).

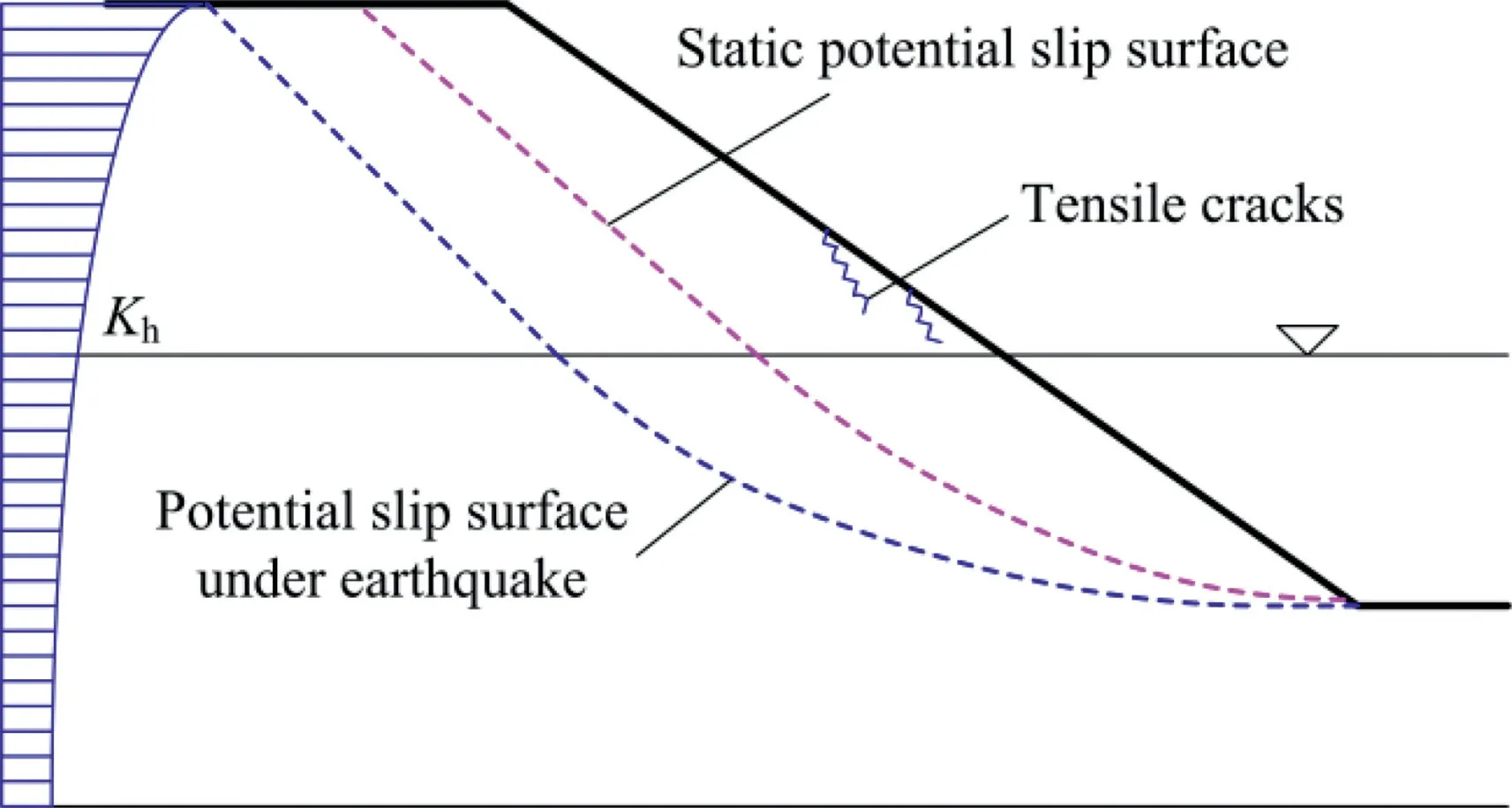
Fig.18.Failure mode of a partially submerged deposit slope.

4.2.4. Shear strain increment

Before the dynamic numerical simulation was conducted,the static calculation was performed first, and the safety factor FS=1.514 was obtained by the strength reduction method.The corresponding potential sliding surface is shown in Fig.16a.In event EQ5,the shear strain increment contours obtained after applying the seismic load for 50 s are shown in Fig.16b.The shear strain develops from the foot of the slope and then towards the upper part thereof.Compared with Fig.16a,the potential shear sliding surface under seismic excitation is located deeper within the slope body due to the effects of horizontal seismic acceleration.It can be seen that the trend of shear slipping is generally similar when comparing the shear strain contour in Fig.16b with the displacement vectors in Fig.11.

Fig.19.Surface tensile cracks at the submergence level.

Fig.20.Sketch of the submerged soil element stress state before and after an earthquake event.

5. Failure mode analysis

Instability modes of partially submerged slopes under static conditions have been extensively studied. Michalowski(2009)used kinematic approach of limit analysis to investigate the influence of pore water pressure and pool water pressure on the stability of the submerged slopes.The most critical failure mechanism of submerged granular slopes was found to have failure surface intersecting slope face,with one intersection point above the water level and the other one below the pool level.Baker et al.(2005)numerically studied the stability of partially submerged cohesionless slopes,and showed that the critical slip surfaces of the cohesionless slope with a small slope angle under no water flow conditions can be composed of three parts,i.e.separate sliding blocks into a driving wedge,stabilizing wedge,and central wedge,as shown in Fig.17.

The static state and failure mode of partially submerged deposit slope under earthquake excitations are different from those of cohesionless soil slope as the cohesion of the deposits in the watercontaining state is not zero.According to the concept of pseudostatic method(Baker et al.,2006;Karray et al.,2018),the distribution of horizontal force coefficient Khis shown in Fig.18 due to the horizontal accelerations being amplified along the elevation,as shown in Figs.4 and 5.From the perspective of the shape of the potential slip surface,the existence of a horizontal inertial force makes the potential shear slip surface develop at a greater depth within the slope body compared with the static potential slip surface,as depicted in Fig.16.In the dynamic centrifuge shaking table tests,some small tensile cracks were also observed on the slope surface above the saturated level after all shaking events,as shown in Fig.19.In view of the stress state,the sketch of the stress state changes in the saturated soil element under the ground motions is shown in Fig.20.The excess pore pressure makes the effective stress Mohr circle move to the left and the shear stress on the soil element near the slip zone increases.Moreover,the seismic loading causes potential damages to soil and reduces the strength thereof,which greatly decreases the stability of such slopes under seismic loading.

The failure mode of submerged deposit slope,combined with the previous results and the present centrifuge test results,can be summarized as follows:

(1)In general,the shear stress near the saturated level at the slope toe is larger than that in other positions under static conditions.

(2)The excess pore pressure is built up in the submerged part of the deposit slope under earthquake excitation.Both the strength parameters and the stiffness modulus of the soil appear to decrease.The slope toe basically undergoes large slipping deformation under such strong seismic action.At the same time,the accelerations in the upper part of the deposit slope are amplified due to the amplification effect of elevation.Consequently,the deposits in the upper part of the slope are dilated and become loose.

(3)The shear strain generally develops from the slope toe to the upper part of the slope.The deformation of the lower part gradually induces slipping of the upper soil.

(4)Landslide will occur as the slip surfaces slowly connect under such strong seismic action.The dynamic shear slipping surface lies deeper inside the slope body than the static potential slip surface.

6. Conclusions

(1)The horizontal PGA amplification factors near the slope surface and in the slope body generally increased with increasing slope elevation.The acceleration response had a significant amplification effect and the PGA amplification factor reached a maximum value of about 2 at the crest of the slope.In addition,due to the differences in the physicomechanical properties of the soil material above and below the saturated level, the accelerations measured by the transducers located near the saturated surface were subjected to a layer-magnification effect.

(2)The excess pore pressure in the slope toe below the saturated liquid surface increased significantly under the effect of ground motion.The maximum value of the excess pore pressure increased with increasing vertical effective stress,while the maximum excess pore pressure ratio showed a decreasing trend therein. No significant liquefaction occurred in the tests.However,the effect of pore pressure accumulation on the stability of such slopes was significant.The maximum excess pore pressure ratio exceeded 70% in these tests, which effectively changed the deformation behavior of the slope near the saturated liquid surface.Nearest to the slope toe is the area where partially submerged deposit slopes are most likely to become unstable under seismic excitation.

(3)The crest settlements accumulated gradually throughout the six-stage centrifuge tests and were most significant in events EQ5(PGA=0.428g)and EQ6(PGA=0.451g)in the 50 s shaking period.The crest settlements continued to increase after the 50 s shaking period due to the dissipation of excess pore pressures.The slope crest settlements caused by the subsequent shaking events were reduced by previous ground motions.

(4)The failure mode of the partially submerged deposit slope under strong earthquake excitation was dominated by slipping near the saturated liquid surface.Initially,the upper part of the slope body was loosened by the strong vibration due to earthquake amplification effects. Meanwhile, the effective stresses in the saturated part of the slope were reduced due to the accumulation of excess pore pressure;nevertheless,liquefaction did not occur.The shear strain at the slope toe gradually increased,and then the deformation of the saturated part of the slope gradually developed.Finally,a continuous slipping surface was gradually formed and a landslide would occur.

Declaration of Competing Interest

The authors wish to confirm that there are no known conflicts of interest associated with this publication and there has been no significant financial support for this work that could have influenced its outcome.

Acknowledgments

The study is supported by the National Natural Science Foundation of China(Grant Nos.41702348 and 41372314),and the Natural Science Foundation of Hubei Province,China(Grant No.2017CFB373).The authors would like to thank Prof.Bin Zhu,Mr.Jinshu Huang and Mr.Gang Yao in Zhejiang University for their help with the centrifuge tests.