江苏辐射沙洲海区潮流对涌浪能量传播的影响

冯 曦, 赵嘉静, 冯卫兵, 李慧超

江苏辐射沙洲海区潮流对涌浪能量传播的影响

冯 曦1, 2, 赵嘉静1, 2, 冯卫兵1, 2, 李慧超1, 2

(1. 海岸灾害及防护教育部重点实验室(河海大学), 江苏 南京 210098; 2. 河海大学 港口海岸与近海工程学院, 江苏 南京 210098)

为研究了江苏辐射沙洲地区潮流场对涌浪能量传播的影响, 本文利用双向耦合的Delft3D- FLOW和SWAN模型进行了对江苏辐射沙洲地区风-浪-潮流的整体模拟。时间尺度, 是表达波能传播速率的有量纲参数。本文利用时间尺度这一物理概念来描述涌浪的波能在地理空间和谱空间中的传播规律。时间尺度越小, 波能的传播速率越快。研究发现, 通过计算和对比波能的时间尺度在地理空间、谱空间内的变化规律, 发现在辐射沙洲地区, 波能时间尺度在谱空间内变化偏大。而在潮流影响下, 涌浪的频率运移表现更明显。通过理想实验的对比, 发现涌浪能量的时间尺度在有潮流明显较无潮流作用时变小, 这反映了潮流对于涌浪能量的传递速率有正向作用。在地理空间上, 波能的时间尺度在涨潮时刻减小, 落潮时刻增大。

潮流; 涌浪; 能量传播过程; 时间尺度; 辐射沙洲

当风渐渐平息之后, 或者当风浪移动到风区以外时, 水面受到惯性力和重力的作用继续保持波动, 此时的水面波动称为涌浪。涌浪能量可以传播很远的距离但却不会明显耗散[1], 其对近岸工程的开展和船舶航运的危害不可小觑[2]。

波浪和潮流是海岸带、海湾和潮汐河口等地区主要的水动力条件。在潮周期内, 波浪的特性将受到调制[3-4], 同时近海波浪能量传播过程受到区域潮流场的影响不可忽视。波流相互作用最早由Longuet- Higgins和Stewart[5]在1962年提出, 其中流对波浪的影响主要是由于流场自身的时空变化引起。波浪特性的改变主要集中在传播轨迹、波能、波要素与波谱分布方面, 其中波能的分布体现了波高特性, 波谱体现了波浪的波能和频率的特性。Kenyon[6]利用射线方程模拟波浪在反向流场中的折射, 波浪波群传播方向会发生偏折, 但还有个别波浪沿着最大流速方向传播。非洲南部东岸海域离岸流和涡流可以使反向的波浪能量增长, 且由于流引起的折射使得波浪耗散在近岸增大[7]。李一平等[8]的研究表明, 太湖中湖流越强对波要素影响越明显。特拉华湾湾口处波浪反射受到潮流影响, 在湾内深槽及湾口外出现与波向反向潮流后导致波能增加[9]。澳大利亚西南海岸反向流造成波高增大以及强流场导致波浪折射增多[10]。辐射沙洲地区, 汤志华等[11]发现潮汐潮流对波高周期有明显调制作用。随着科研设备技术的发展, 有关波谱特性的研究也日趋多见, 例如Suh等[12]。在流的影响下, 波谱结构也会发生变化, 例如Lambrakos[13]观测到波流相互作用对随机波波谱的具有影响。

本文研究区域南黄海辐射沙洲位于射阳河口与长江口北部之间, 以弶港和洋口港之间的黄沙洋为主轴向外海辐射(图1b)[14]。何小燕等[15]学者发现, 在江苏近海, 夏季发生的涌浪是破坏海岸建筑物的主要因素之一。在弶港外15 km处的条子泥地区是辐射沙脊群的顶点, 该处旋转潮波与前进潮波辐聚, 潮流整体场呈辐射状分布, 与沙脊潮道分布一致。此处潮流场流向复杂且近岸地区流速较大。例如在弶港以北地区平均大潮流速大于1.5 m/s, 主流方向与岸线平行, 属强潮流区[16-17]。在此地区特殊的强潮流场中, 波浪传播亦受到不小的影响[6]。

流对波能波谱的影响已有部分研究, 但在特殊的辐射状流场中, 潮流对波能和波谱的影响还需要进一步探讨。本文以南黄海辐射沙洲地区特殊的潮流场作为背景, 详细地研究波浪在地理空间及谱空间的能量传播功率, 其中, 对谱空间的研究能清晰表现出涌浪在方向上与频率上的能量转移状况, 结果显示涌浪在潮流作用下发生折射与频移, 进而通过对一维、二维波谱的研究量化能量在谱空间的改变程度。研究潮流对涌浪能量传播的影响对确定合理的近岸工程设计参数及航运具有重要的意义。

1 模型介绍与验证

1.1 模型介绍及设置

本文采用Delft-3D FLOW和SWAN耦合模型。耦合模型日趋成熟, 已获认可并在应用中得到了良好的结果[18-20]。波浪模型解决了折射、绕射和波流耦合的相互作用。波浪和流模块耦合将流模块的平均流速传递给SWAN, SWAN再将波浪参数传递给流模块。

流模块计算范围为119°E—123.5°E, 31°N—35°N, 北至射阳河口, 南至长江口地区, 涵盖整个南黄海辐射沙洲海域, 采用矩形网格, 网格精度为2 000 m (图1a), 我们所关心的研究区域在120.5°E—122.5°E, 32°N—34°N之间(图1a黄色虚线框)。开边界条件为时间序列的潮位数据, 来源为NAO.99b (http: //www. miz.nao.ac.jp/staffs/nao99/index_En.html), 时间精度为1 h, 初始条件选用时空变化的ECMWF风场, 时间精度为6 h, 空间分辨率为12 km。底摩阻曼宁系数采用区域变化的参数, 根据水深计算0.015+0.01/||。

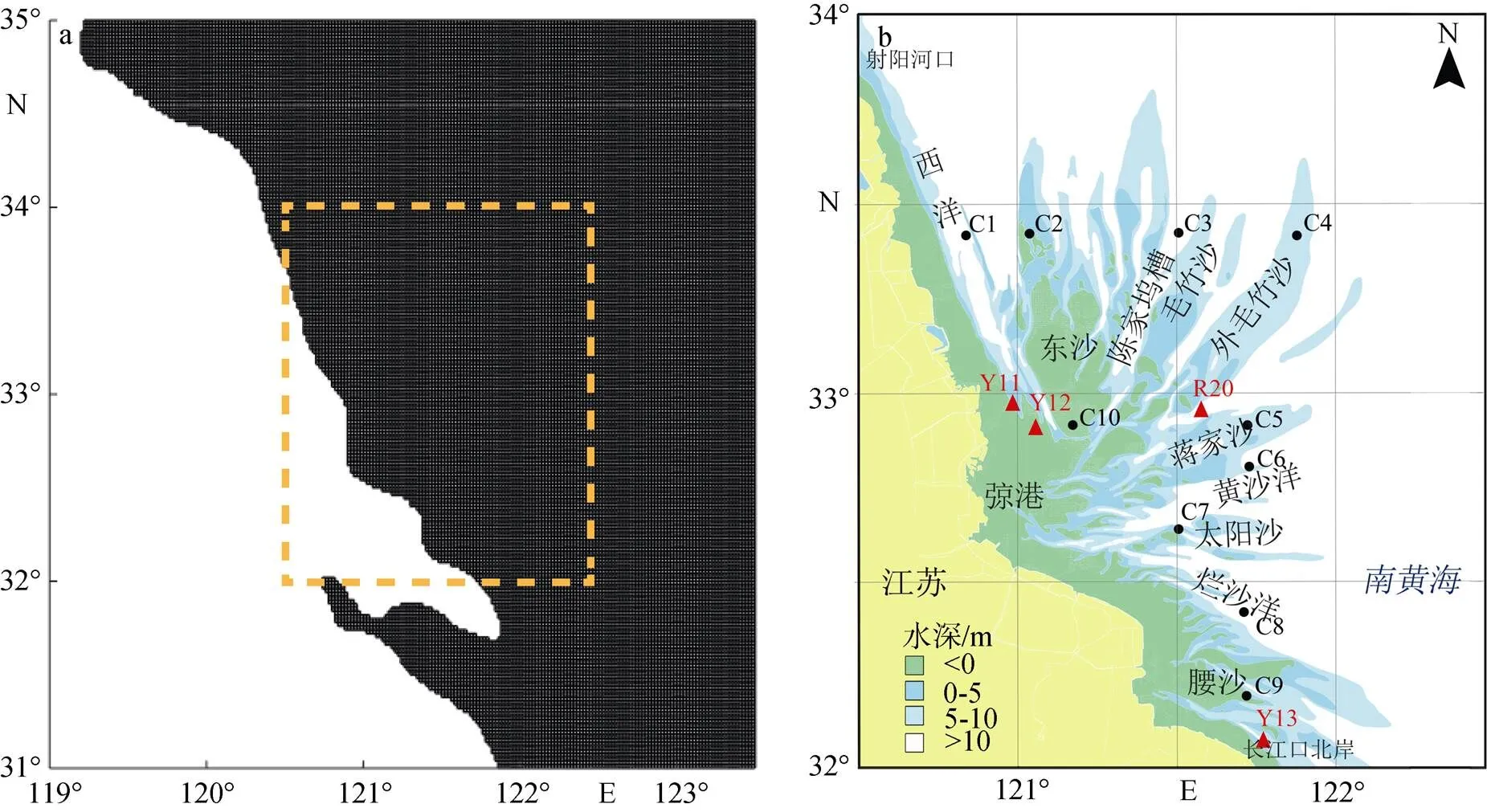
图1 (a)模型网格及(b)辐射沙洲区域的水深图(a中黄框所示区域)

波浪模块的计算网格区域、精度与坐标系与流模块相同, 在耦合过程中将潮流项传递给波浪模块。波浪边界为波谱造波方式, 给定波浪的谱峰周期p、有效波高s与来向p。物理过程项考虑折射、绕射、三波-波交互作用、深度诱导破碎耗散、底摩阻耗散以及白帽耗散, 参数选择为默认。

Delft3D耦合模型已经能很好的模拟波流耦合的过程, Delft3D-FLOW的二维潮流控制方程为(1), 二位潮流和方向的动量方程为公式(2)、(3):

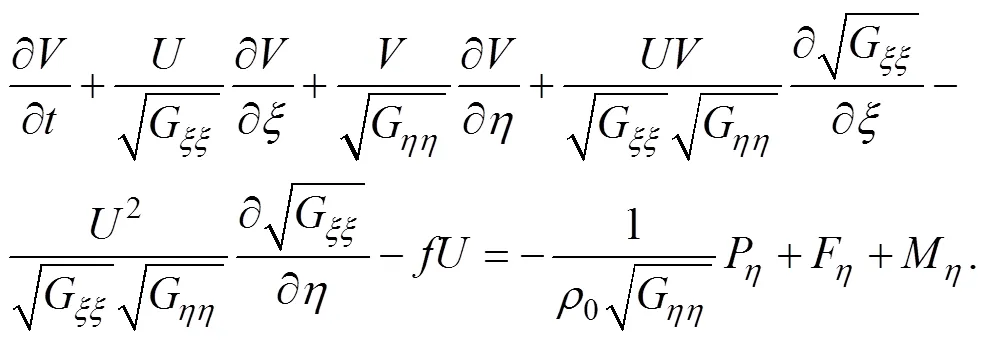
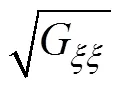
Delft-SWAN模型控制方程为[22]:

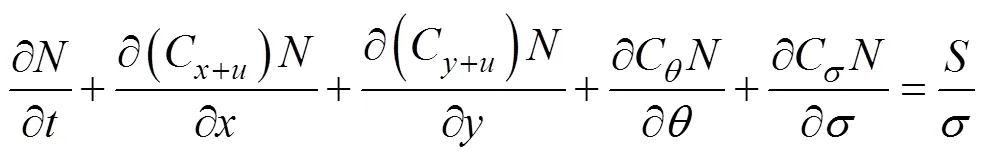
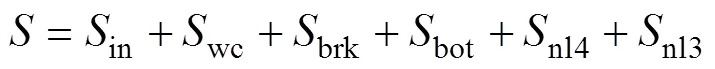
1.2 模型验证

本模型模拟过程为真实潮流场下的理想化波浪试验。为了验证流模型模拟的准确性, 设置一组模型试验, 模拟时间为2007年1月整月。本文选取4个测站点Y11、Y12、R20、Y13的实测数据与模拟值进行对比(位置见图1b红色三角), 其中Y11, Y12和R20位于近岸沙脊上, R20位于外海潮流通道内, 各点的位置及实测资料时间段见表1。

潮位、潮流流速及流向对比图较为直接地展示在图2中, 模型较好地模拟了辐射沙洲潮流场。经过计算潮位的相关系数R最高可达0.99。潮流流速及流向在R20处模拟最好, 因为其位于潮道中线, 潮流流向受到地形限制变得单一, 加之潮道内地形变动不剧烈, 故模拟结果最佳。潮流流速及流向受到地形精度的影响极大, 外加辐射沙洲地形常年处于变动中[22], 给潮流场的模拟带来了一定的困难, 例如Y12测点靠近辐射沙洲潮流场辐射顶点弶港, 由于此处是波能与潮能的汇聚点, 地形变动频繁, 所以无论是潮位还是潮流模拟均有些偏差。

表1 测点的位置及实测资料信息

1.3 试验组次

为了探究潮流对涌浪能量传播的影响, 本文共设置6组试验, 试验组次见表2。其中, Case1—3考虑了不同谱峰周期p和来波方向p; Case4—6依次为未考虑波流耦合情况下, Case1—3试验的对照组。

1.4 潮流场概述

本文以2013年7月8日14时与20时为例, 图3a与3b分别展示了在涨潮和落潮时刻的潮流场和潮流梯度, 图中颜色表达了涨潮和落潮时刻的潮流流速, 黑色箭头表达了潮流流向, 图3c和3d分别为涨潮和落潮时刻的潮流流速梯度。图中, 黑线为15 m等深线, 是辐射沙洲海域沙脊的外轮廓。涨潮时刻, 潮流顺着潮道向辐射沙洲顶点汇聚, 潮道及近岸沙洲地区流速较大, 且由远及近逐渐增大。落潮时刻潮流从沙洲顶点向外辐散, 流速较大的地区主要为潮道。落潮时刻流速大与涨潮时刻。近岸岸线地区流速骤减。在沙脊和潮道交界处以及岸线附近地区流速梯度较大(图3c和3d)。

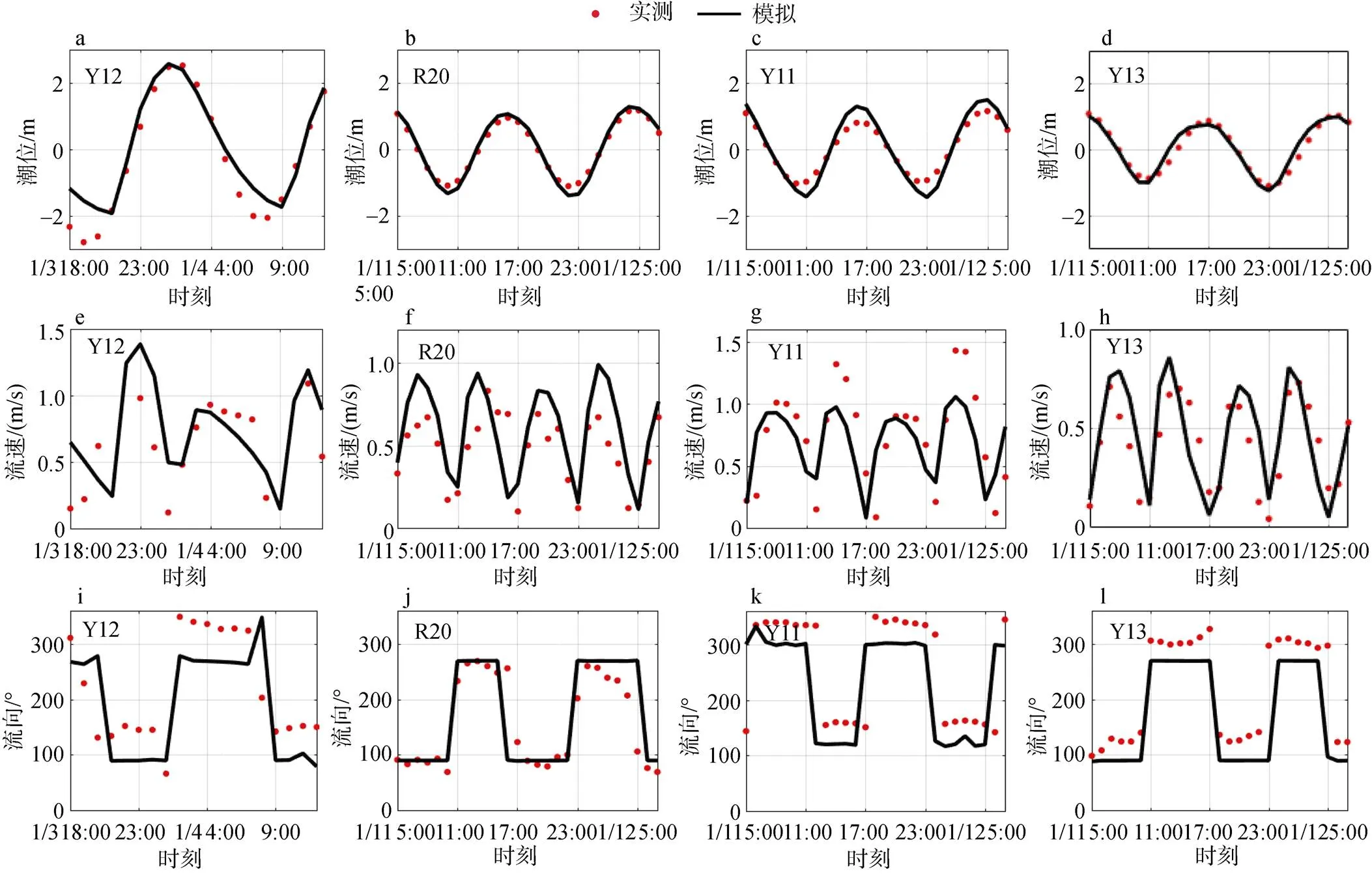
图2 浮标测点处模拟验证

注: 子图a—d: 潮位验证; e—h: 潮流流速验证; i—l: 潮流流向验证

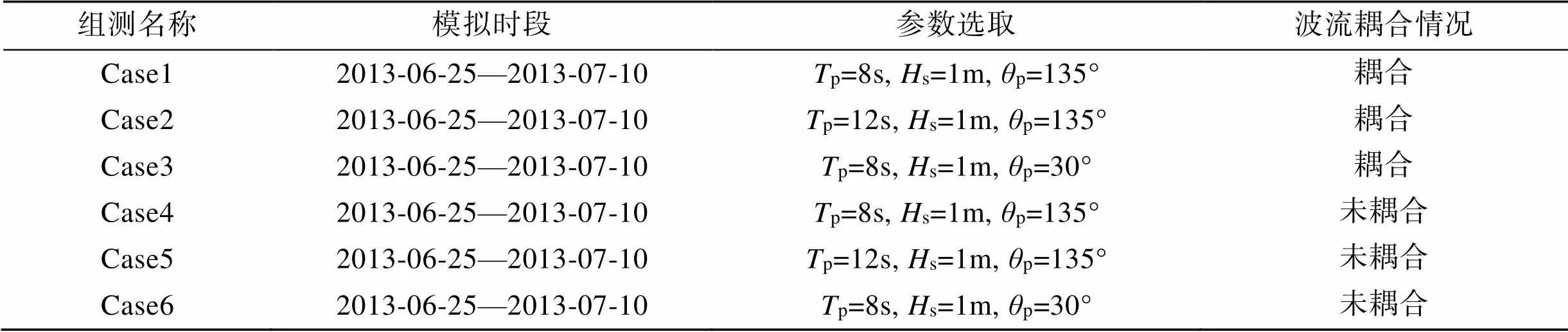
表2 试验组测

1.5 波能的时间尺度

能量传播过程的标准化时间尺度τ可以更好地展示能量的传播规律[23]。标准化的时间尺度表达式如下所示:

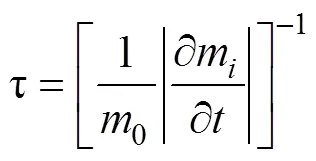
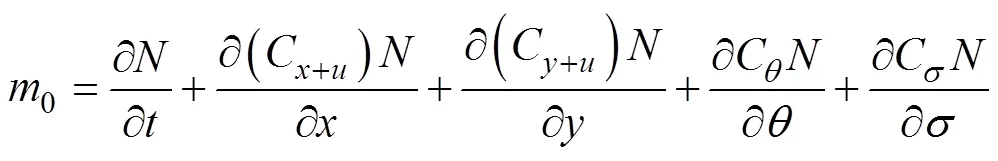
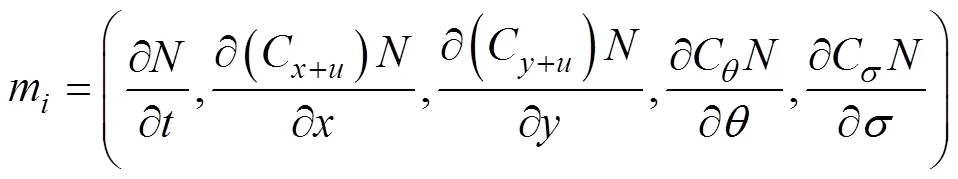
式中代表时间尺度, 是表达波能传播速率的有量纲参数, 其单位为s。式中,0为总波能,m是任意单项波能值, 例如在下文中可用τ, y代表波浪在地理空间、方向的传播速率, 其表达式为:

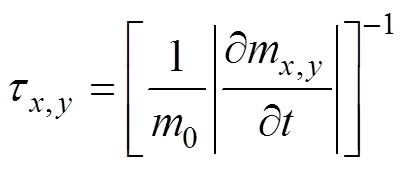
τx, y越小则代表波能在x、y间传播过称中变化越快, 公式(7)中。τσ表达了波浪能量在σ空间的传播过程, mσ可以理解为涌浪的频移, τσ表达了能量在频率方向上传输的快慢。而能量在θ空间的传播过程可以理解为由流和非平稳水深变化引起的折射现象, τθ可以反映折射程度的强弱。从图4中可以看出, 在波流耦合的情况下, 波能在辐射沙洲区域内(图4黑线勾勒部分)的各项时间尺度均较小。其中能量在频移在辐射沙洲内外尤为明显。对比图3可以发现, 流速梯度也在辐射沙洲内部, 特别是潮流通道和沙脊的交界处较大, 而这里也是各波能项的时间尺度较小处。

注: 子图a、c: 涨潮; b、d: 落潮

2 潮流对涌浪能量传播的影响

为了更加清楚地展示能量传播速率在潮流通道和沙脊上的分布规律, 我们在研究区域选取C1—10共10个测点进行个例分析(位置如图1b所示)。其中, C1、3、6、8位于潮流通道内, 其余测点分布在沙洲沙脊上。

2.1 潮流对涌浪能量在x、y空间传播的影响

从图5a可以看出, 位处沙脊位置的τ, y值普遍小于潮流通道内的τ, y值。无论在潮流同道中, 还是在沙脊上, 涨潮时刻的τ, y值普遍小于落潮时刻的τ, y值。这表明了波能在沙脊上的传播速率大于在潮流通道内。由于m, y代表了波浪受地形影响产生的浅水效应, 及水流对波浪产生的影响, 可见在沙脊上, 浅水效应更显著。涨潮时, 潮流增加了涌浪波能在地理空间上的传播速率(图5a)。

图4 涨潮和落潮时刻波能在各个空间的时间尺度

注: 子图a、c、e: 涨潮时刻; b、c、d: 落潮时刻; 子图a、b: x、y空间传播的时间尺度; 子图c、d: 波能在σ空间传播的时间尺度; 子图e、f: 波能在θ空间传播的时间尺度

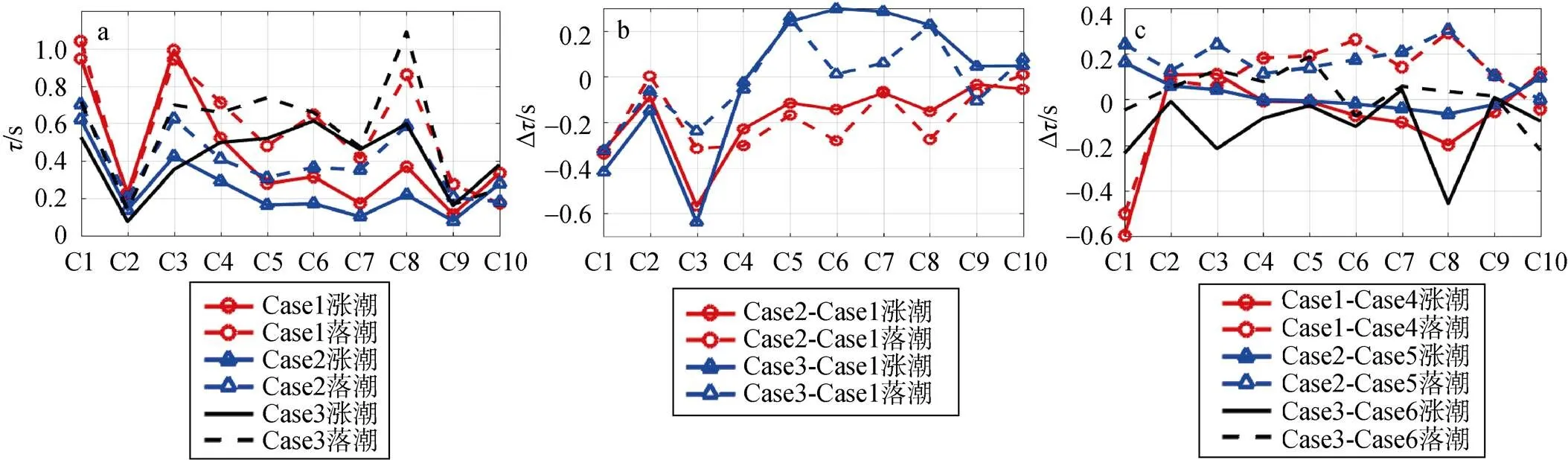
图5 在C1—10位置地理空间内波能的时间尺度(τx, y)及其变化量

注: 子图a: Case1—3涨落潮时刻的τ, y值; 子图b: 在不同波况下τ, y的变化量; 子图c: 有无潮流时τ, y的变化量

表3 辐射沙洲各处(C1—10)τ均值在涨落潮时刻的差值

通过对比有潮流和无潮流下的时间尺度τ, y(图5c), 可以更清晰地发现在迎浪位置处,τ, y在落潮时刻普遍增加,τ, y在涨潮时刻普遍减小。而在背浪地区,τ, y受潮流场、外海涌浪来向, 和外海涌浪周期的影响不明显。

2.2 潮流对涌浪能量在谱空间传播的影响

2.2.1 能量在空间传播的时间尺度

图6a展示了C1—10位置的τ在涨落潮时的大小。由图6a可见(或者由此可见)涨落潮时刻τ值没有明显的变化规律。在大部分区域(除C1、C4位置),τ符合涨潮时刻小于落潮时刻的普遍规律。这说明涨潮时, 潮流促进波能在频率上的转变。

图6b对比了不同的涌浪波况下τ的变化。由图6b可见(或者由此可见),p增大使τ整体减小(红色实线);p改变使τ在迎浪位置减小, 而在背浪位置增加。通过表2可以看出, 当p一致时,p增长后Δτ均值在涨潮时刻为–0.556 s, 落潮时刻为–0.151 s; 当p一致时,p改变后Δτ均值在涨潮时刻为0.095 s, 落潮时刻为–0.172 s。

图6c对比了在有无潮流作用时,τ的变化。有潮流与无潮流时τ量级截然不同。在潮流的影响下, 能量在空间的传输在大部分地区开始活跃, 波浪频移现象明显。在辐射沙洲地区的变化。结合表2中第3—5列可以看出, Δτ均负且量值很大。由此可见, 涨落潮期间, 波流耦合作用明显, 波能在频率空间内的转移加剧。

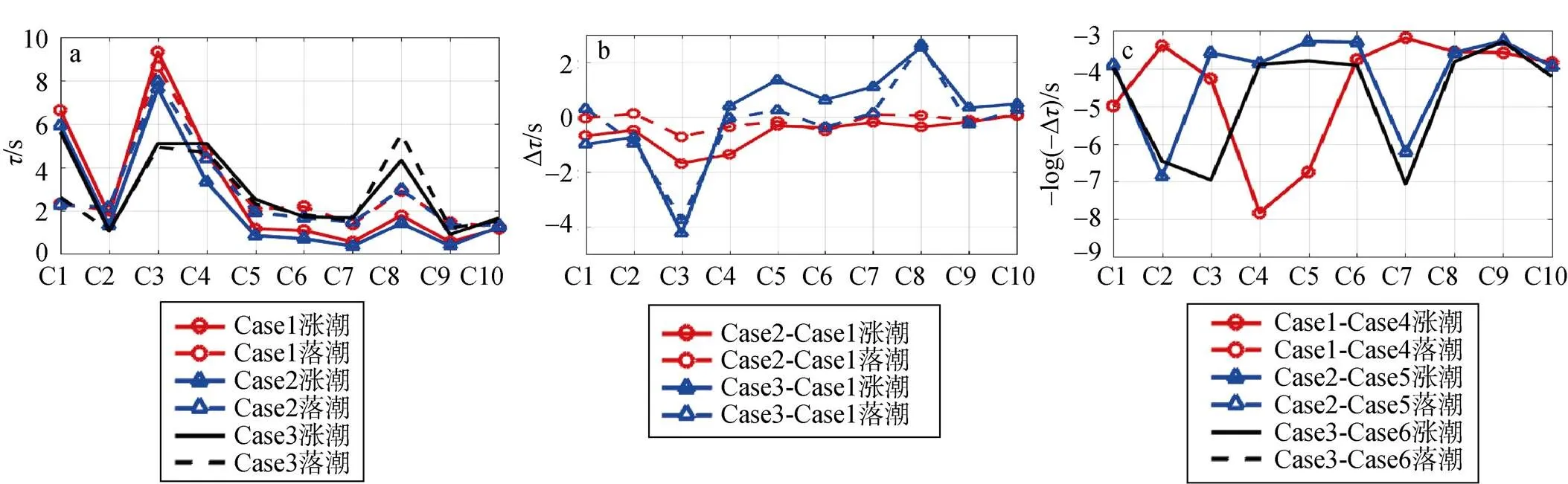
图6 在C1—10位置频率空间内波能的时间尺度(τσ)及其变化量

注: 子图a: Case 1—3涨落潮时刻的τ值; 子图b: 在不同波况下τ的变化量; 子图c: 有无潮流时τ的变化量

2.2.2 能量在空间传播的时间尺度

图7a显示了在Case1情况下τ在C1—C10位置处的分布规律。对比图6a,τ值整体小于τ, 与τ, y量级一致。类似τ,τ在辐射沙洲的北部海域总体较大, 即在北部海域受折射影响较小。

图7b反映了p和p对τ分布的改变规律。其结论基本与τ, y的变化规律保持一致(图5c)。T的增长使τ在涨潮时刻变化值为–0.333 s, 落潮时刻为–0.303 s(详见表2)。对比Case1与Case2, 在p相同时,p的增大总体会使τ呈增大的趋势。这说明除了少数区域外, 随着涌浪的谱峰周期增加, 波浪传播时所受折射效应增大, 波能传播速率变低。对比Case1与Case3, 在p相同时, 随着p自东南来向转为东北来向, 在背离东北向来波的地区C5—9,τ在涨潮时刻增大, 波能传播速率变小。

图7c对比了在有无潮流的情况下,τ的变化规律。由图可见, 除涌潮的来波方向为30°时,τ在涨潮时刻有明显的降低,τ在其余辐射沙洲上各测点没有明显的持续增大或变小的趋势。说明潮流在与涌浪风向基本平行时, 对涌浪的折射影响大, 而在与涌浪方向基本垂直时折射影响较小。在西洋水道中的C1和弶港近潮滩处的C10两测点,τ在潮流作用下, 无论涨落潮, 始终表现出降低的趋势。这一方面可能由于当涌浪传播到近岸时, 波向基本与岸线垂直, 且与潮流方向平行有关; 另一方面也说明在近岸水深较浅处, 潮流对波浪的折射影响增强。

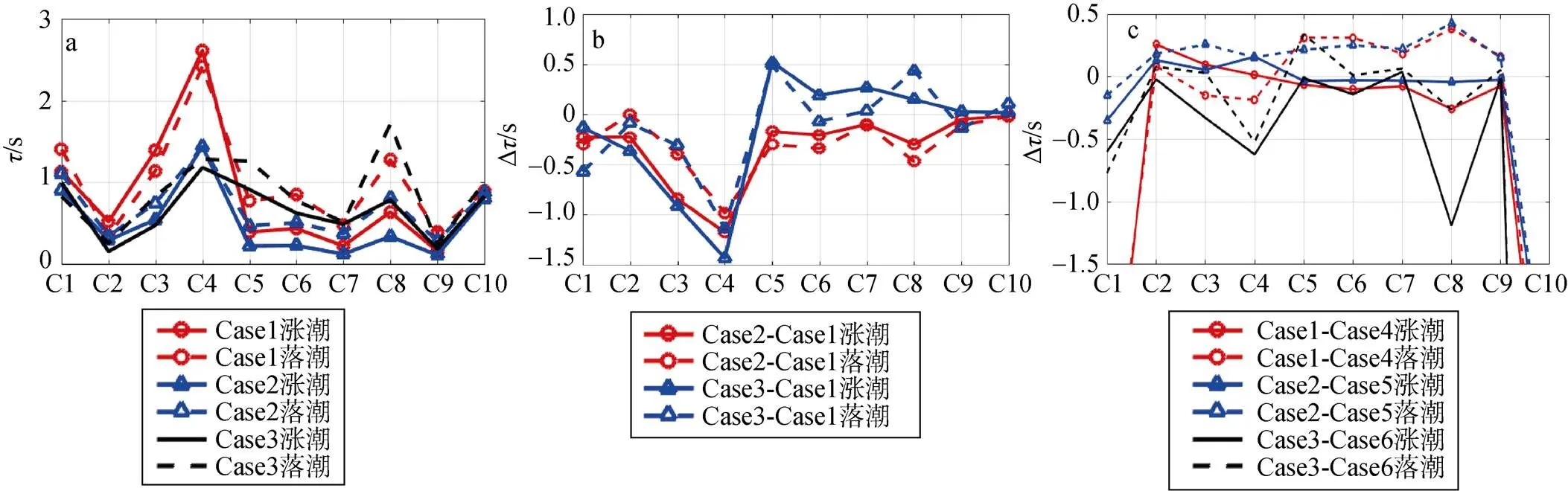
图7 在C1—10位置方向空间内波能的时间尺度(τθ)及其变化量

注: 子图a: Case1—3涨落潮时刻的τ值; 子图b: 在不同波况下τ的变化量; 子图c: 有无潮流时τ的变化量

2.2.3 潮流对波谱结构的改变

为了更加清楚地看出潮流对能量在谱空间的传播影响, 本文选取了陈家坞槽中三个点A1、A2、A3(图8a右上), 分别绘制各点涨落潮时刻与无潮流情况下的1D波谱图。其中, 红实线为涨潮, 蓝实线为落潮, 黑虚线为无潮。在这三个点, 流速由远海及近岸依次增大, 且各点的主要潮流方向基本为东北至西南。

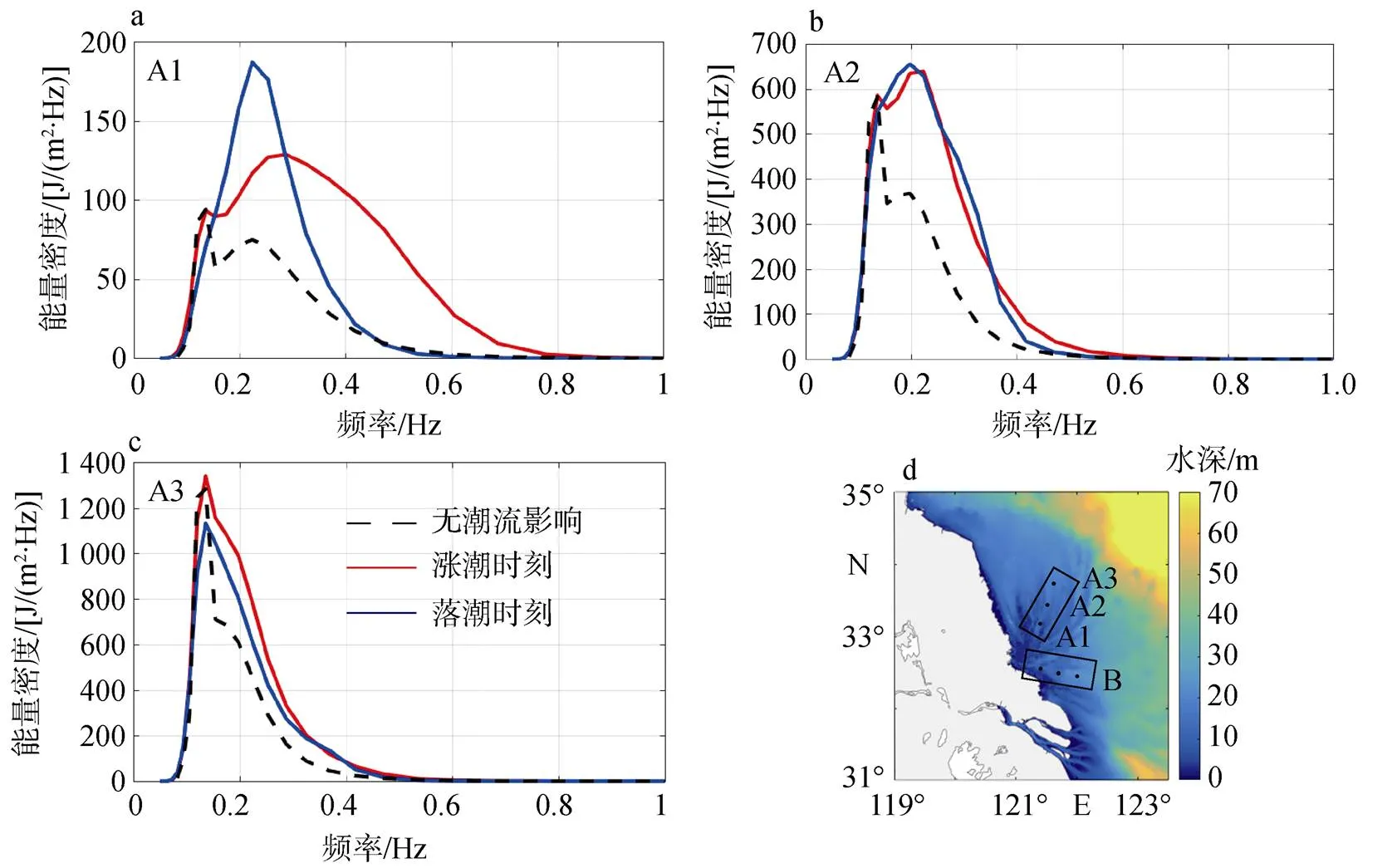
图8 涨落潮与无潮时在A1、A2、A3位置处1D波谱对比图

注: 子图a: 位置A1; 子图b: 位置A2; 子图c: 位置A3

从图8可见, 自A1—3, 在潮流作用下波谱谱形发生的相对变化, 依次变小。总体而言, 近岸处, 由于潮流流速大, 谱形改变也较大, 能量的频移更剧烈。在A1处, 在较强的涨潮流作用下, 谱峰向高频移动。在潮道内, 流速越大, 导致涌浪的谱峰周期的改变和总波能的变化越明显, 涨潮时刻总波能大于落潮时刻。在烂沙洋另选了三个点(图8中B区), 表现出类同A1—3的规律, 故不做图展示。

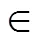
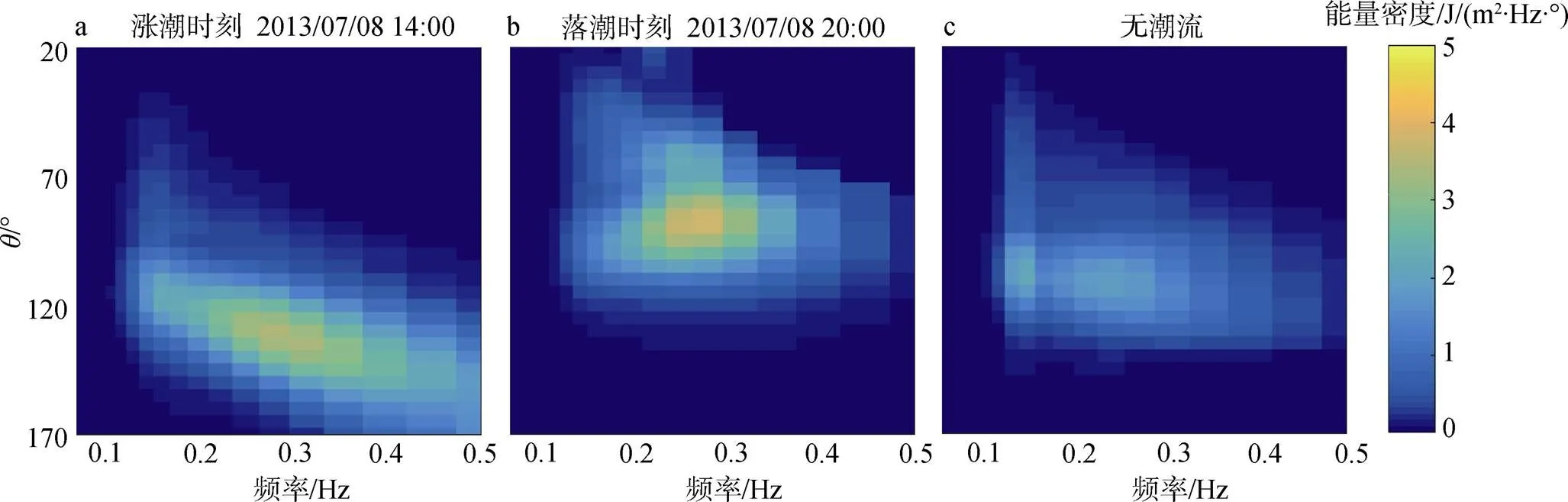
图9 A1点处2D波谱对比

注: 子图a: 涨潮时刻; b: 落潮时刻; c: 无潮流作用时

3 总结

本文利用Delft-3D FLOW和SWAN模型对比了在有无潮流作用时, 涌浪在辐射沙洲地区的传播特征。利用时间尺度这一物理量, 衡量了波浪传播过程中, 在地理空间、频谱空间和方向空间范畴内的变化速率和变化规律。研究发现辐射沙洲地区, 涌浪的传播符合以下规律:

(1) 在潮流作用下, 涌浪的总体时间尺度在辐射沙洲地区明显较无潮流作用时变小, 且涌浪能量的传播与潮流流速梯度场有一定的关联。

(2) 涌浪在传播过程中, 沙洲沙脊位置处, 波能在地理空间和谱空间的时间尺度均小于邻近潮道位置。

(3) 波能在地理空间和方向空间内的时间尺度小于在谱空间的时间尺度, 潮流对涌浪的频率运移影响明显, 对波谱结构的改变也较显著。

[1] Snodgrass F E, Groves G W, Hasselmann K F, et al. Propagation of ocean swell across the Pacific[J]. Philo­sophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1966, 259(1103): 431-497.

[2] Faltinsen O. Sea Loads on Ships and Offshore Structures[M]. Cambridge: Cambridge university press, 1993.

[3] Gonazález F I. A case study of wave–current–bathymetry interactions at the Columbia River Entrance[J]. Journal of Physical Oceanography, 1984, 14(6): 1065-1078.

[4] Tolman H L. Effects of tides and storm surges on North Sea wind waves[J]. Journal of Physical Oceanography, 1991, 21(6): 766-781.

[5] Longuet-Higgins M S, Stewart R W. Radiation stress and mass transport in gravity waves, with application to ‘surf-beats’[J]. Journal of Fluid Mechanics, 1962, 13(4): 481-504.

[6] Kenyon K E. Wave refraction in ocean currents[J]. Deep Sea Research & Oceanographic Abstracts, 1971, 18(10): 1023-1034.

[7] Schumann E H. Changes in energy of surface gravity waves in the Agulhas Current[J]. Deep Sea Research & Oceanographic Abstracts, 1976, 23(6): 509-518.

[8] 李一平, 逄勇, 刘兴平. 太湖湖流对波浪的影响机制研究[J]. 水利学报, 2007(S1): 308-313. Li Yiping, Pang Yong, liu Xingping. Study on the influence mechanism about current to wave in Lake Taihu[J]. Shuilixuebao, 2007(S1): 308-313.

[9] Kukulka T, Jenkins R L, Kirby J T, et al. Surface Wave Dynamics in Delaware Bay and Its Adjacent Coastal Shelf[J]. Journal of Geophysical Research: Oceans, 2017, 122(11): 8683-8706.

[10] Wandres M, Wijeratne E M S, Cosoli S, et al. The Effect of the Leeuwin Current on Offshore Surface Gravity Waves in Southwest Western Australia[J]. Journal of Geo­physical Research: Oceans, 2017, 122(11): 9047-9067.

[11] 汤志华, 郑晓琴, 曹翔宇, 等. 潮汐和潮流影响下苏北辐射沙洲海域波浪模拟分析[J]. 海洋预报, 2015, 32(2): 24-30. Tang Zhihua, Zheng Xiaoqin, Cao Yangyu, et al. Numerical simulation and analysis of waves with tide and currents in the radial snadbanks[J]. Marine Forecasts, 2015, 32(2): 24-30.

[12] Suh K D, Kwon H D, Lee D Y. Some statistical chara­cteristics of large deepwater waves around the Korean Peninsula[J]. Coastal Engineering, 2010, 57(4): 375-384.

[13] Lambrakos K F. Wave-current interaction effects on water velocity and surface wave spectra[J]. Journal of Geophysical Research, 1981, 86(C11): 10955-10960.

[14] 王颖. 黄海陆架辐射沙脊群[M]. 北京: 中国环境科学出版社, 2002. Wang Ying. Radiative Sandy Ridge Field on Continental Shelf of the Yellow Sea[M]. Beijing: China Environmental Science Press, 2002.

[15] 何小燕, 胡挺, 汪亚平, 等. 江苏近岸海域水文气象要素的时空分布特征[J]. 海洋科学, 2010: 34(9), 44- 54. He Xiaoyan, Hu Ting, Wang Yaping, et al. Spatial and temporal distribution characteristics of hydrological meteorological elements in coastal waters of Jiangsu Province[J]. Marine Sciences, 2010, 34(9): 44-54.

[16] 诸裕良, 严以新, 薛鸿超. 南黄海辐射沙洲形成发育潮流数学模型[J]. 水动力学研究与进展(A辑), 1998, (4): 473-480. Zhu Yuliang, Yan Yixin, Xue Hongchao. Tidal current numerical model for the formation and development of Radial Sandbank in the Yellow Sea[J]. Journal of hydro­dynamics, 1998, (4): 473-480.

[17] 诸裕良. 南黄海辐射状沙脊群动力特征研究[D]. 南京: 河海大学, 2003. Zhu Yuliang. Hydromechanical characteristics of the Radial Sandbanks in the Southern Yellow Sea[D]. Nanjing: Hohai University, 2003.

[18] Lesser G R, Roelvink J A, Kester J A T M, et al. Deve­lopment and validation of a three-dimensional morphological model[J]. 2004, 51(8-9): 883-915.

[19] Sutherland J, Walstra D J R, Chesher T J, et al. Evaluation of coastal area modelling systems at an estuary mouth[J]. Coastal Engineering, 2004, 51(2): 119-142.

[20] Allard R, Dykes J, Hsu Y L, et al. A real-time nearshore wave and current prediction system[J]. Journal of Marine Systems, 2008, 69(1): 37-58.

[21] Booij N, Ris R C, Holthuijsen L H. A third‐generation wave model for coastal regions: 1. Model description and validation[J]. Journal of Geophysical Research Oceans, 1999, 104(C4): 7649-7666.

[22] Xing F, Wang Y P, Wang H V. Tidal hydrodynamics and fine-grained sediment transport on the radial sand ridge system in the southern Yellow Sea[J]. Marine geology, 2012, 291: 192-210.

[23] Holthuijsen L H, Zijlema M, van der Ham P J. Wave physics in a tidal inlet[C]//Coastal Engineering- International Conference, 2009: 437-448.

Effect of tidal currents on the progress of swell energy propa­gation in Jiangsu radial sand ridges

FENG Xi1, 2, ZHAO Jia-jing1, 2, FENG Wei-bing1, 2, LI Hui-chao1, 2

(1. Key Laboratory of Coastal Disaster and Defense, Ministry of Education, Hohai University, Nanjing 210098, China; 2. College of Harbor, Coastal and Offshore Engineering, Hohai University, Nanjing 210098, China)

To study the effect of the tidal current on the process of swells in the Jiangsu radial sand ridges (JRSRs), a two-way coupled Delft3D-FLOW and SWAN modeling system was used to simulate wind-wave-tide triple interactions in the JRSRs. A time scale is a dimensional parameter that can express the wave energy transmission rate. Time scales were used to describe the propagation process of swell energy in geographical and spectral spaces. This study, by calculating and comparing the time scales of wave energies in geographical and spectral spaces in the JRSRs, found that the time scales of wave energy in the spectral space were larger than those in the geographic space. The tidal current has a significant influence on the frequency-shift of swells spectra. Through comparison experiments, the time scale was found to dramatically reduce when the tidal current was present. This finding indicates that tidal current had a positive influence on the transmission rate of swell energy. In the geographical space, the time scale of wave energy decreased during flooding tide and increased during ebbing.

tidal current; swells; the progress of the energy propagation; time scale; radial sand ridges

Sep. 4, 2019

TV139.2

A

1000-3096(2020)03-0023-11

10.11759/hykx20190904001

2019-09-04;

2019-12-20

国家自然科学基金(51709091); 江苏省自然科学基金(BK20170874); 中央高校基金(2017B005)

[National Natural Science Foundation of China, No. 51709091; Jiangsu Natural Science Foundation of China or Natural Science Foundation of Jiangsu Province, No. BK20170874; Fundamental Research Funds for the Central Universities, No.2017B005]

冯曦(1987-), 女, 江苏南京人, 博士, 主要从事海岸带水动力和海岸带灾害研究的研究, E-mail: xifeng@hhu.edu.cn

(本文编辑: 丛培秀)