基于平均应变能密度准则的裂纹断裂扩展特性分析

黄如旭，谢晓忠，谢 锋，黄进浩，万正权

(中国船舶科学研究中心 深海载人装备国家重点实验室，江苏 无锡 214082)

0 引 言

由于结构应力状态复杂性或裂纹分布随机性使得工程结构中的裂纹通常为混合型裂纹。用于研究混合型裂纹断裂问题的经典断裂理论假设裂纹尖端应力场仅由奇异项控制，这些断裂理论主要包括最大环向应力准则（MTS 准则）[1]、应变能密度因子准则（SED准则）[2]以及平均应变能密度准则（ASED 准则）[3]。与MTS 准则和SED 准则仅考虑裂纹前缘某一点的应力或应变能不同，ASED 准则考虑裂纹尖端某一区域内所有应力分量对裂纹扩展的影响并假设裂纹尖端以临界距离rc为半径的圆形面积内平均应变能密度达到其临界值时裂纹发生起裂扩展，具有明确的物理意义。已有研究表明[4–7]，裂纹尖端应力场常数项对裂纹扩展过程中的裂纹尖端塑性区形状、起裂扩展角及起裂扩展条件的影响不可忽略。本文基于ASED 准则理论围道积分核心思想[3,8–10]，综合考虑裂纹尖端应力场奇异项和常数项对裂纹扩展的影响，建立I-II-III 混合型裂纹起裂扩展条件计算式。在此基础上，系统分析常数项T 应力对裂纹起裂扩展条件的影响；最后，以承受纵向拉伸、侧向压缩双轴疲劳载荷作用下的平板表面I 型裂纹为研究对象，结合修正的平均应变能密度准则分析常数项T 应力对疲劳裂纹扩展寿命的影响。

1 修正平均应变能密度准则

柱坐标系下，包含奇异项及常数项的裂纹尖端应力场为[11]：

式中：σij（i，j=1，2，3）为柱坐标系下与裂纹平面呈θ 角；距离裂纹尖端为r 的一点应力分量（见图1）；KI，KII，KIII和T 分别为I 型、II 型、III 型应力强度因子和非奇异项T 应力；υ'为材料常数，平面应力问题取为0，平面应变问题取为材料泊松比υ。

弹性体中一点应变能密度表达式为[8–9]：

式中：μ 为剪切模量；参数κ 为材料参数，平面应变问题κ=3–4υ，平面应力问题κ=( 3-υ)/(1+υ)。

图 1 裂纹尖端应力场Fig. 1 Stress field around crack tip

根据ASED 准则[3]，当裂纹尖端以临界距离rc为半径的圆形面积内的平均应变能密度达到临界值时裂纹发生起裂扩展，如图2 所示。

图 2 裂纹尖端断裂控制区域[9-10]Fig. 2 Fracture progress zone

结合式（1）～式（8），采用Mathematica 计算，得到综合考虑裂纹尖端应力场奇异项和常数项的平均应变能密度：

根据ASED 准则，裂纹起裂判据表达式为：

对于纯I 型裂纹有KII=0，KIII=0，T=0。同时，纯I 型裂纹起裂时KIf=KIc，于是以临界距离rc为半径的圆形面积内的平均应变能密度临界值

联立式（9）、式（10）和式（11）可得修正平均应变能密度准则I-II-III 混合型裂纹起裂判据为：

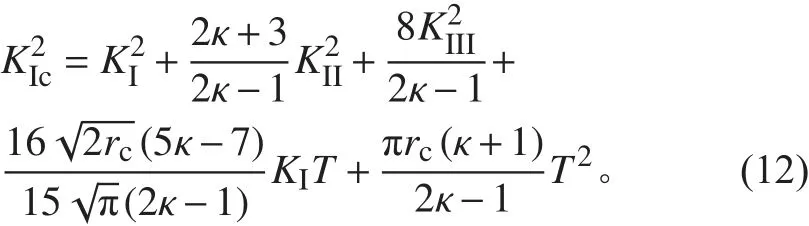
2 常数项对裂纹断裂特性影响分析

2.1 对I-II 混合型裂纹断裂特性影响分析

对于I-II 混合型裂纹，KIII=0，式（12）蜕化为III 混合型裂纹起裂扩展条件计算式[12]。研究I-II 混合型裂纹时引入无量纲参数双轴因子B 和参数α[7]：

式中：Keff为有效应力强度因子[7]；a 为裂纹长度；rc为断裂控制区域临界距离，可由进行估算[7]，其中σt为材料拉伸极限。反映常数项T 应力的参数Bα 为：

引入参数Bα 后，修正平均应变能密度准则I-II 混合型裂纹起裂判据为[12]：

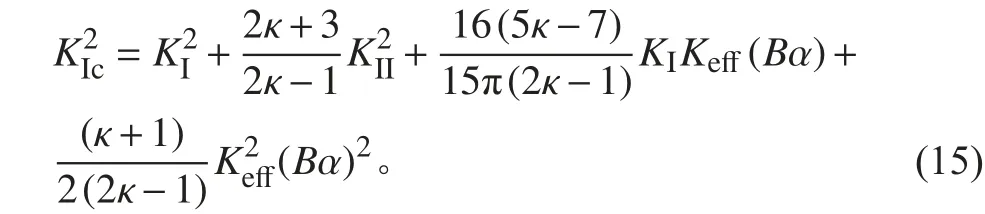
平面应变状态，泊松比υ=0.3 时不同Bα 情况下的修正平均应变能密度准则断裂判据曲线（Bα=0 时为ASED 准则，作为比较基准），如图3 所示。

图 3 常数项对I-II 混合型断裂判据曲线影响Fig. 3 The effect of T-stress on fracture limit

由图3 可以看出，考虑常数项T 应力影响的断裂判据曲线均在ASED 准则（Bα=0）断裂判据曲线之内，即T 应力降低了材料裂纹起裂阻力，且|Bα|越大裂纹断裂极限值越低；当|Bα|相同时，正的T 应力（Bα 为正值）对应的断裂判据曲线在负的T 应力（Bα 为负值）对应的断裂判据曲线之下，即|Bα|相同时，正T 应力要比负T 应力更容易发生断裂。

2.2 对I 型、II 型裂纹断裂特性影响分析

对于I 型裂纹（KII=0），修正平均应变能密度准则I 型裂纹断裂判据为[8]：

对于II 型裂纹（KI=0），修正平均应变能密度准则II 型裂纹断裂判据为：

平面应变状态，泊松比υ=0.3 时I 型裂纹断裂极限值KIf随Bα 的变化曲线如图4 所示。

图 4 I 型裂纹断裂极限随Bα 变化曲线（KII=0）Fig. 4 Variation of fracture limit for mode I crack

由图4 可以看出，T 应力对I 型裂纹断裂极限值KIf有很大的影响，当T 应力为负值时，KIf随T 应力的增大而增大直到达到最大值（KIfmax=1.02KIc），随后随T 应力的继续增大而下降；T 应力在区间为–0.48＜Bα＜0 时I 型裂纹断裂极限值KIf反而大于KIc，可理解为此区间内T 应力增大了I 型裂纹的断裂韧性，但引起的增大幅度并不高，可忽略不计，即–0.4 8 ＜Bα＜0 时，T 应力对I 型裂纹断裂极限KIf几乎没有影响；正的T 应力将降低I 型裂纹断裂极限值KIf；相同|Bα|时，正T 应力对应的I 型裂纹断裂极限KIf低于负T 应力对应的I 型裂纹断裂极限KIf，如当Bα=1.0 时，KIf=0.75KIc（考虑T 应力时的I 型裂纹断裂韧性降低了25.0%）当Bα=–1.0 时，KIf=0.88KIc，即考虑T 应力时的I 型裂纹断裂韧性降低了12.0%。

平面应变状态，泊松比υ=0.3 时II 型裂纹断裂极限值KIIf随Bα 的变化曲线，如图5 所示。

图 5 II 型裂纹断裂极限随Bα 变化曲线（KI=0）Fig. 5 Variation of fracture limit for mode II crack

由图5 可以看出，对于II 型裂纹来说，T 应力降低了II 型裂纹断裂极限值KIIf；相同|Bα|时，II 型裂纹断裂极限KIIf相同，II 型裂纹断裂极限值KIIf受T 应力的大小影响，与T 应力的正负无关。当|Bα|=1.0 时，KIIf=0.51KIc，以ASED 准则纯II 型裂纹断裂极限值KIIf=0.63KIc作为参考基准，考虑T 应力时的II 型裂纹断裂韧性降低了19.1%。

3 常数项对裂纹扩展影响分析

工程结构中最常见、最危险的裂纹形式为I 型表面裂纹，选取双轴载荷作用下平板半椭圆表面I 型裂纹研究常数项T 应力对疲劳裂纹扩展寿命的影响，其中纵向载荷为拉伸属性，侧向载荷为压缩属性。考虑T 应力影响的I 型裂纹KII=0，T≠0。按照修正平均应变能密度准则，I 型裂纹等效应力强度因子Keq为：

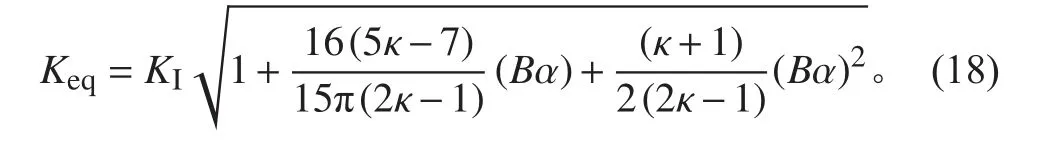
疲劳裂纹扩展计算参量ΔKeq，只需将式（18）中KI替换为ΔKI=（1–R）KI即可，为简化研究，取应力比R=0。

3.1 准静态分析

纵向施加拉伸载荷P1=300 MPa，侧向施加压缩载荷P2=500 MPa。双轴载荷作用下的平板模型示意如图6 所示。平板长度为L=600 mm，宽度为W=120 mm，厚度为t=35 mm；半椭圆表面裂纹位于平板中心，初始裂纹长度为2c=5 mm，深度为a=2 mm，裂纹形状示意如图7 所示。

采用20 节点solid95 单元建立含半椭圆表面I 型裂纹平板有限元模型，如图8 所示。坐标原点位于平板表面裂纹长度中心位置，y 轴为裂纹长度方向，z 轴为平板长度方向。在平板2 个侧面施加500 MPa 的压应力，在平板纵向一端施加300 MPa 的拉应力。边界条件为：平板纵向端面面心施加uy=0，纵向端面板厚一半高度上所有节点ux=0，未施加纵向载荷的端面所有节点施加uz=0。

图 6 双轴载荷含半椭圆表面I 型裂纹平板结构Fig. 6 Sketch of surface crack plate under biaxial fatigue load

图 7 半椭圆表面裂纹示意图Fig. 7 Sketch of surface crack

图 8 双轴疲劳载荷下平板有限元模型Fig. 8 FE model under biaxial fatigue load

3.2 疲劳裂纹扩展寿命分析

疲劳裂纹扩展分析时，计算参量分别选取为传统方法的I 型应力强度因子范围ΔKI和等效应力强度因子范围ΔKeq，选取裂纹最深点A 为计算参考点（见图7），裂纹扩展深度由2 mm 扩展至14 mm 时，最深点A 处的参数Bα 变化曲线，如图9 所示。等效应力强度因子变化范围ΔKeq（取κ=3–4υ，平面应变状态），如图10 所示。

由图9 可以看出，在裂纹扩展过程中参数Bα 为负值，总体趋势为随裂纹扩展而逐渐变小，Bα 的变化区间为–2.5～–1.0（裂纹在扩展中将不会发生偏折[6–7]）。由图10 可知，裂纹扩展过程中应力强度因子随裂纹扩展而逐渐增大；裂纹扩展过程中裂纹尖端等效应力强度因子范围ΔKeq高于不考虑T 应力时的I 型应力强度因子范围ΔKI。

图 9 参数Bα 随裂纹深度变化情况Fig. 9 Variation of parameter Bα

图 10 应力强度因子变化范围ΔK 随裂纹深度变化情况Fig. 10 Variation of ΔK

裂纹扩展过程中应力强度因子变化范围直接决定了裂纹扩展寿命。根据裂纹前缘参考节点的扩展情况计算裂纹扩展寿命，当参考点的ΔaA足够小时，可近似将应力强度因子变化范围按常数处理。选择工程中常用的Paris 模型计算裂纹扩展寿命，某钢材料疲劳裂纹扩展速率参数如下式：

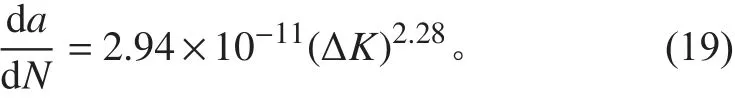
计算得到的裂纹扩展寿命如图10 所示。由图10可以看出，对于承受纵向受拉、侧向受压双轴载荷作用的平板表面裂纹，裂纹深度由2 mm 扩展至14 mm（0.4t）时：不考虑T 应力影响时的裂纹扩展寿命为72 508 次；根据修正平均应变能密度准则，计算得到考虑常数项T 应力影响的裂纹扩展寿命为35 752 次，约为传统裂纹扩展寿命的49%。

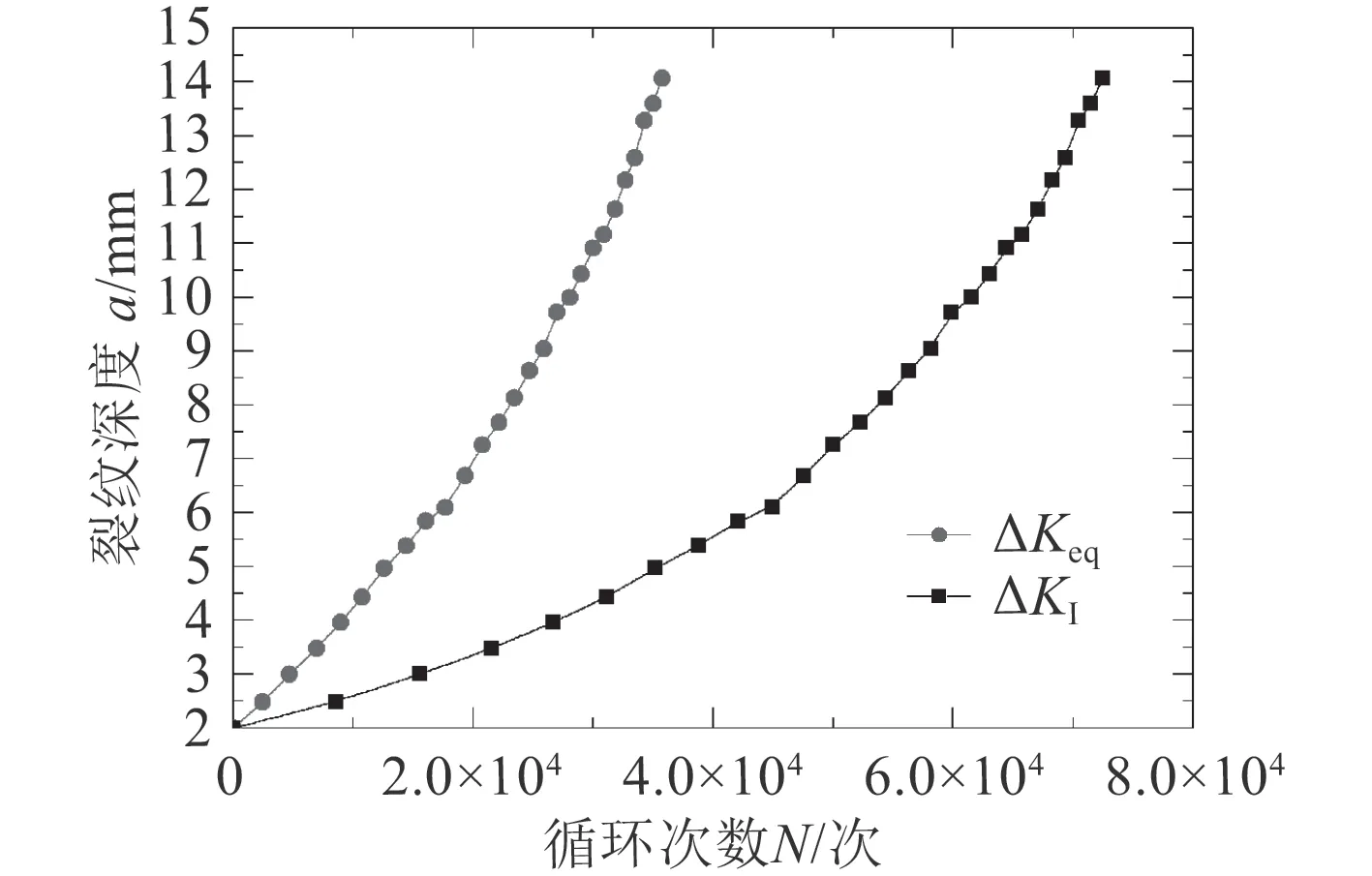
图 11 裂纹扩展寿命计算结果Fig. 11 Fatigue crack growth results

4 结 语

本文根据考虑常数项T 应力影响的修正平均应变能密度准则，研究常数项T 应力对I 型、II 型和I-II混合型裂纹起裂扩展特性的影响。基于修正平均应变能密度准则研究常数项T 应力对双轴疲劳载荷作用下的平板表面裂纹扩展寿命的影响。得到以下结论：

1）常数项T 应力降低了材料裂纹起裂阻力，且|Bα|越大裂纹断裂极限值越低，|Bα|相同时正T 应力下的裂纹更易起裂扩展。

2）对于I 型裂纹，当T 应力为负值时，KIf随T 应力的增大而增大直到达到最大值，随后随T 应力的继续增大而下降；相同|Bα|时，正T 应力对应的I 型裂纹断裂极限KIf低于负T 应力对应的I 型裂纹断裂极限KIf；对于II 型裂纹，相同|Bα|时，II 型裂纹断裂极限KIIf相同，即II 型裂纹断裂极限值KIIf受T 应力大小影响，与T 应力正负无关。

3）计算得到的纵向受拉、侧向受压双轴疲劳载荷平板表面I 型裂纹，由深度2 mm 扩展至14 mm 时，扩展寿命计算结果约为传统不考虑T 应力影响时裂纹扩展寿命计算结果的49%，不考虑T 应力影响的传统计算方法将会严重高估I 型裂纹的扩展寿命。