微积分的创立与第二次数学危机

谢周艳 胡先富

【摘要】本文从数学发展史的角度，探索微积分产生的历史背景到微积分的创立过程，及第二次世界危机产生和结束的过程。

【关键词】微积分  数学危机  无穷小量

17世纪，函数概念被采用后，产生了微积分，是继欧几里得几何之后，全部数学中的一个最大的创造;为17、18世纪的科学创新提供了锐利的工具，使人类的理性思维达到了一个新的高度。揭示微积分创立过程中蕴含着的文化价值与人文精神，适时融入课程教学，有利于提高知识的趣味性，破除学生对微积分认知的“神秘感”。从而增强学生对数学的情感与态度，这也是践行“三全育人”要求的高等数学课程思政的有效途径。

一、促使微积分产生的历史背景

微积分主要是为处理17世纪的科学问题而产生的。16至17世纪，机械与枪炮的使用、远洋航行的发展、光学仪器的研制、矿山的开发等，促进了机械力学、流体力学、运动学以及几何光学等学科的蓬勃发展，这些学科的研究提出了以下四类问题急需数学来解决：

第一类问题：对于作变速运动的物体，已知物体移动的距离与时间的函数关系，求物体在任意时刻的瞬时速度和瞬时加速度;反过来，已知物体的加速度与时间的函数关系，求速度和距离。这类问题是研究物体运动时直接出现的，17世纪所涉及到的速度和加速度每时每刻都在变化。比如，计算瞬时速度，就不能像计算平均速度那样，因为在给定的瞬时，物体移动的距离和所用的时间都是“0”，而“”是无意义的。但是，物体在它运动的每一时刻必有速度，这也是无疑的。在已知速度公式求移动的距离时，也遇到了同样的困难。

第二类问题：确定物体运动的方向及光学中曲线的切线问题。

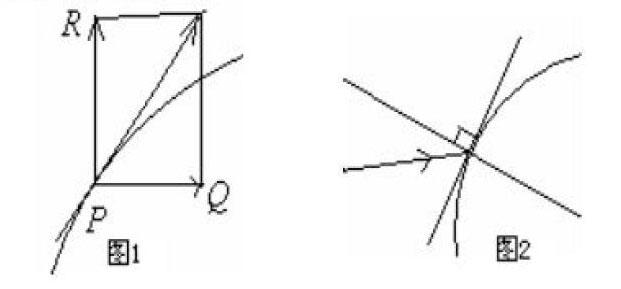
在运动的研究中，运动物体在它的轨迹上任一点处的运动方向，是轨迹的切线方向。例如，从炮筒里发射的炮弹的运动方向是水平速度Q和垂直速度R的合成速度的方向，即是PQ和PR构成的平行四边形的对角线方向，这条对角线即为炮弹运动的轨迹（曲线）上一点P处的切线（如图1）。

光学是17世纪一门较重要的科学研究，透镜的设计直接吸引了费尔马、笛卡尔、牛顿等科学家，要研究光线通过透镜的通道，必须知道光线射入透镜的角度以便应用反射定律，重要的角是光线同曲线的法线间的夹角，法线是垂直于切线的，所以问题在于求出曲线的切线（如图2）。这就使得求任意曲线的切线问题变得不可回避。

在当时，“切线”本身的意义是没有解决的。

第三类问题：求函数的最大值与最小值问题。

炮弹在炮筒里射出，它运行的水平距离，即射程，信赖于炮筒对地面的倾斜角，即发射角，一个“实际”的问题是求能获得最大射程的发射角。

研究行星的运动也涉及最大值和最小值的问题，例如求行星离开太阳的最远和最近的距离。

第四类问题：求曲线的长（例如，行星在已知时期中移动的距离），曲线围成的面积，曲面围成的体积，分布不均匀的物体重心与质量，一个体积相当大的物体（如行星）作用于另一个物体上的引力等。

这些问题至少被17世纪几十个数学家探索过，如法国的费尔马、笛卡尔、罗伯瓦、笛沙格，英国的巴罗、瓦里士，德国的开普勒，意大得的卡瓦列利等，他们都是建立微积分的先驱者。17世纪上半叶，许多数学家一系列前驱性的工作，已在不同方向向微积分的大门逼近。求切线、求变化率、求极值和最值以及面积、体积等基本问题，在当时是被作为不同的类型来处理的，在方法上缺乏足够的一般性。作为微积分主要特征的微分与积分的互逆关系，当时也曾有少數人在特殊场合模糊地指出，但没有作为一般规律提出来。17世纪中叶数学家们面临的重要课题是如何将这些分散的方法综合起来形成统一的理论。

二、微积分的创立

17世纪下半叶，英国的牛顿与德国的莱布尼兹在总结前人大量研究成果的基础之上， 以敏锐的洞察力发现求切线问题、求瞬时速度问题、求最值问题有着共同之处，各种求积问题的处理（求弧长、求面积、求体积）在方法上的相同性;同时认识到了求积问题（积分学的中心问题）与求切线问题（微分学的中心问题）的互逆关系，同时将这种互逆关系明确地作为一般规律揭示出来，并将其作为建立微积分普遍算法的基础。经进一步的归纳、抽象、概括，他们站在更高的高度将以往个别的贡献和分散的努力综合为统一的理论——创立了微积分。他们是在各自的国家是独立地完成了这一任务的。

牛顿与莱布尼兹的最大功绩是把两个貌似毫不相关的问题：求切线问题和求积问题联系在一起。他们的工作，概括起来主要有以下四点：

第一、把各种有关概念和方法的几何形式、力学形式等，变成解析形式，为统一、抽象奠定基础。

第二、用变化率（或微分）概念来统一一切与切线、速度有关的概念。

第三、统一求积问题。

第四、给出求变化率（或微分）与求积的互逆关系。

以上四项工作标志着微积分作为一门统一的学科的诞生。

牛顿研究微积分侧重于从运动学来考虑，莱布尼兹却侧重于几何学来考虑;牛顿建立微积分以无穷小瞬（无穷小量）为基础， 莱布尼兹则以微分（无穷小量）为基础。因此，微积分的逻辑基础是无穷小量，微积分在早期也称为无穷小量分析。莱布尼兹在1684年发表了现在世界上认为最早的微积分文献，他所创设的微积分符号很多，如dx，dy，等，一直沿用至今。

下面是牛顿求函数变化率（导数）的方法：

牛顿在1671年写成《流数法和无穷级数》一书，该书于1736年才出版，在该书中， 牛顿把连续变量叫做流量，记作x，y等，认为流量是随时间变化而变化的，把这些流量的变化率叫做流数，x和y的流数记作和。把一个无限小的时间间隔称为瞬，记作o（无穷小量）。该书主要解决了以下两个问题：

问题1：已知流量x，y之间的函数关系（即y=f（x）），求两个流量x，y的流数的比：（实际上是求y对x的变化率）。

问题2：问题1的逆问题，已知一个含流数的方程，求流量之间的关系。

牛顿对问题1的解决方法如下：

假定两个流量x，y之间的关系为y=xn，用“o”表示“无穷小的时间间隔（称为瞬）”，用o和o分别表示x和y的无穷小增量（或称为x和y的瞬），则有关系：y+o=（x+o）n，

由二项式展开得：

y+o=xn+nxn-1·o+x·（o）2+···

消去两端相等的部分（y=xn）得：

o=nxn-1·o+x·（o）2+···

两边同除以“o”得：=nxn-1·+x·（）2o+···

略去所有含有“o”的项得： =nxn-1·，即=nxn-1

用现在的记号是=nxn-1

微积分的建立，极大的推动了数学的发展，过去很多初等数学束手无策的问题，运用微积分，往往迎刃而解，显示出微积分学的非凡威力。

三、第二次数学危机

17世纪的微积分没有严密的逻辑基础， 许多地方存在漏洞， 人们对微积分的逻辑基础无穷小量的认识是模糊不清的，无论是牛顿的无穷小瞬，还是莱布尼兹的微分，都是一种似是而非的、含糊不清的。

1734年，英国哲学家贝克莱以税利的眼光，一针见血地将矛头指向微积分的逻辑基础——无穷小量，指出“牛顿在求流量y=xn的流数时，先给一个无穷小的时间间隔“o”，求出流量y的增量o，再两边同除以“o”，说明“o”非零;然后略去所有含有“o”项，即“o”为零，这岂不是自相矛盾;无穷小量“”既等于零，又不等于零，召之即来，挥之即去，这真是荒谬。”他说“微积分是建立在沙滩之上的，经不起考验的，无穷小量“o”是逝去的灵魂。”而牛顿用这种方法得到的结论经力学和几何学的应用证明又是正确的。无穷小量“o”究竟是不是零？如果是零，又怎么能用它做除数，如果不是零，又怎么能把包含无穷小量的那些项去掉呢？无穷小量及其分析是否合理？这样在推敲微积分的逻辑基础时，数学界出现了混乱局面，为此而引起数学界甚至哲学界长达一个半世纪的争论，导致了数学历史上第二次危机。

为了解决微积分理论的基础问题，许多数学家经过了大量的努力，直到19世纪20年代，柯西于1821年建立了系统的极限理论，提出了“無穷小量是以零为极限的变量”解决了当时模糊不清的无穷小量问题。后来维尔斯特拉斯进一步把微积分建立在坚实的极限理论基础之上，从而才结束了第二次数学危机。微积分的创立使人类第一次真正实现了对运动与变化的定量分析和数学研究，给数学界带来了革命性的变化，在各个科学领域得到广泛的应用。

基金项目：重庆市2019年教学改革研究项目“高等数学课程思政的研究与实践”（项目编号：193424）。

作者简介：谢周艳（1988-），女，汉族，湖南邵阳人，重庆城市管理职业学院，研究方向：偏微分方程、数学教育;胡先富（1964-），男，汉族，重庆市人，重庆城市管理职业学院，研究方向：高等数学、数学教育。