基于遗传算法优化BP神经网络的电解碲电源

刘 静，柳 成，曲永印

(1.北华大学电气与信息工程学院，吉林 吉林 132021；2.吉林化工学院，吉林 吉林 130022)

1 电解碲生产过程

电解碲是将经过提纯的二氧化碲作为溶质，溶入氢氧化钠溶液中配制成电解液，以普通铁板作为电解阳极，不锈钢板作为电解阴极，在一定电压、电流、温度条件下，在电解槽内两电极上进行电化学反应，从而在阴极得到产品碲的过程.电解原理见图1.

在碲电解过程中，电解电源的电压、电流是否稳定直接决定着电解碲的纯度及效率.电源电压是碲电解过程中可直接测量的一个参数，也是最能反映电解槽状态变化的参数，因此，电解碲电源是电解过程中的关键设备.

2 主电路设计

电解碲电源是低压大电流设备.本文研究设计一台稳定高效的800 A/40 V大功率直流电源，电解过程中向4个串联电解槽通入直流电，每个电解槽电压为10 V.电解碲电源实际是AC-DC-DC变换器[9]，直流电源的输入是三相交流电，前级采用PWM整流器减小输入侧谐波含量，提高功率因数；后级采用ZVS移相全桥变换器扩大输出直流电压范围[10].主电路拓扑见图2.

2.1 PWM整流器数学模型

本文主要采用具有电流解耦的双闭环控制策略对电解碲电源前级PWM整流器控制系统进行改进.数学建模是研究PWM整流器控制理论的第一步.将网侧滤波电感的电流和输出端的电容电压作为状态量，为便于设计控制策略，通过坐标变换，建立d-q两相旋转坐标系下的数学模型[11]：

(1)

由式(1)可以看出，dq坐标系下电流仍存在耦合项ωLiq、ωLid，同时受到ud、uq及电网电压ed、eq的影响.通过引入扰动补偿，实现d轴和q轴电流id、iq的耦合项消失，实现独立解耦控制.

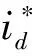
2.2 PWM整流器控制系统

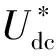
2.3 参数设计

为满足电解碲电源电压、电流的需求，获取稳定、可靠的直流电，提高电解效率和产品质量，设计电路元器件参数，见表1.

表1 电路元器件设计参数Tab.1 Design parameters of circuit components

3 遗传算法优化BP神经网络PID控制策略

3.1 BP神经网络

BP神经网络模型由输入层、隐含层、输出层组成[12]，见图4.学习过程为正向传播和误差反向传播两个过程.本文神经网络输入神经元为电压给定值Udc、电压误差值e和误差变化率ec，输出层为PID参数kp、ki、kd，采用S函数作为激活函数，输出最优的PID参数用于电压环控制.

由于BP神经网络的误差对权重值的变化不敏感，误差梯度变化很小、迭代次数多、收敛速度较慢，反向误差传播的过程中采用梯度下降法极易陷入局部最优.因此，需对其进行优化.

3.2 GA-BP模型优化

遗传算法是一种模拟自然选择和遗传机制的随机搜索算法，具有内在的隐并行性和更好的全局寻优能力[13].因此，使用遗传算法优化BP神经网络的权值和阈值，使优化后的网络既具备BP神经网络的自学习能力及非线性拟合的优点，又具备遗传算法收敛快速、高效的全局搜索能力.结合本系统，遗传算法部分采用由构建好的BP神经网络计算的平均误差作为适应度函数，具体计算公式为

其中：yi为神经网络第i个节点的期望值；n为网络输出节点数；oi为第i个节点的计算值.遗传算法中，选择算子采用轮盘赌法，个体ai被选中的概率为

式中：f(ai)为每个个体轮盘赌法的选择概率.

当个体采用实数编码时，两个不同染色体am和an在j位的交叉操作为

当变异算子以一定概率对第i个个体的第j个基因发生变异时，变异操作为

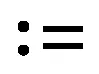
式中：amax、amin为基因的上、下限；g为当前迭代次数；gmax为最大迭代次数；R为[0，1]之间的随机数.遗传算法优化BP神经网络学习算法的流程见图5.

3.3 仿真试验

在电解碲电源系统中，前级采用电压和电流双闭环控制，通常电压外环PID的响应速度小于电流内环.在利用BP神经网络对PID进行优化时，由于BP神经网络的误差对权重值的变化不敏感，收敛速度较慢，极易陷入局部最优，因此，采用并行搜索全局寻优的遗传算法优化BP网络对电压环进行控制.通过建立数学模型和分析控制策略，利用MATLAB软件搭建GA-BP神经网络PID controller模块，见图6.

在仿真试验中，BP神经网络采用3层结构：3-10-3，即3个输入分别为电压给定值Udc、电压误差值e和误差变化率ec，3个输出即PID参数kp、ki、kd，隐含层节点数为10.学习速率为0.1，惯性因子为0.01，网络学习最大平方误差为10-5，遗传算法中种群个数为20，迭代次数为200，交叉概率为0.84，变异概率为0.009.GA-BP控制下的交流侧电网电压与入网电流、A相电压和电流波形见图7，电解碲电源在GA-BP、BP和PID控制下的前级直流侧电压波形见图8，电源后级直流侧输出电压与电流波形见图9、图10.

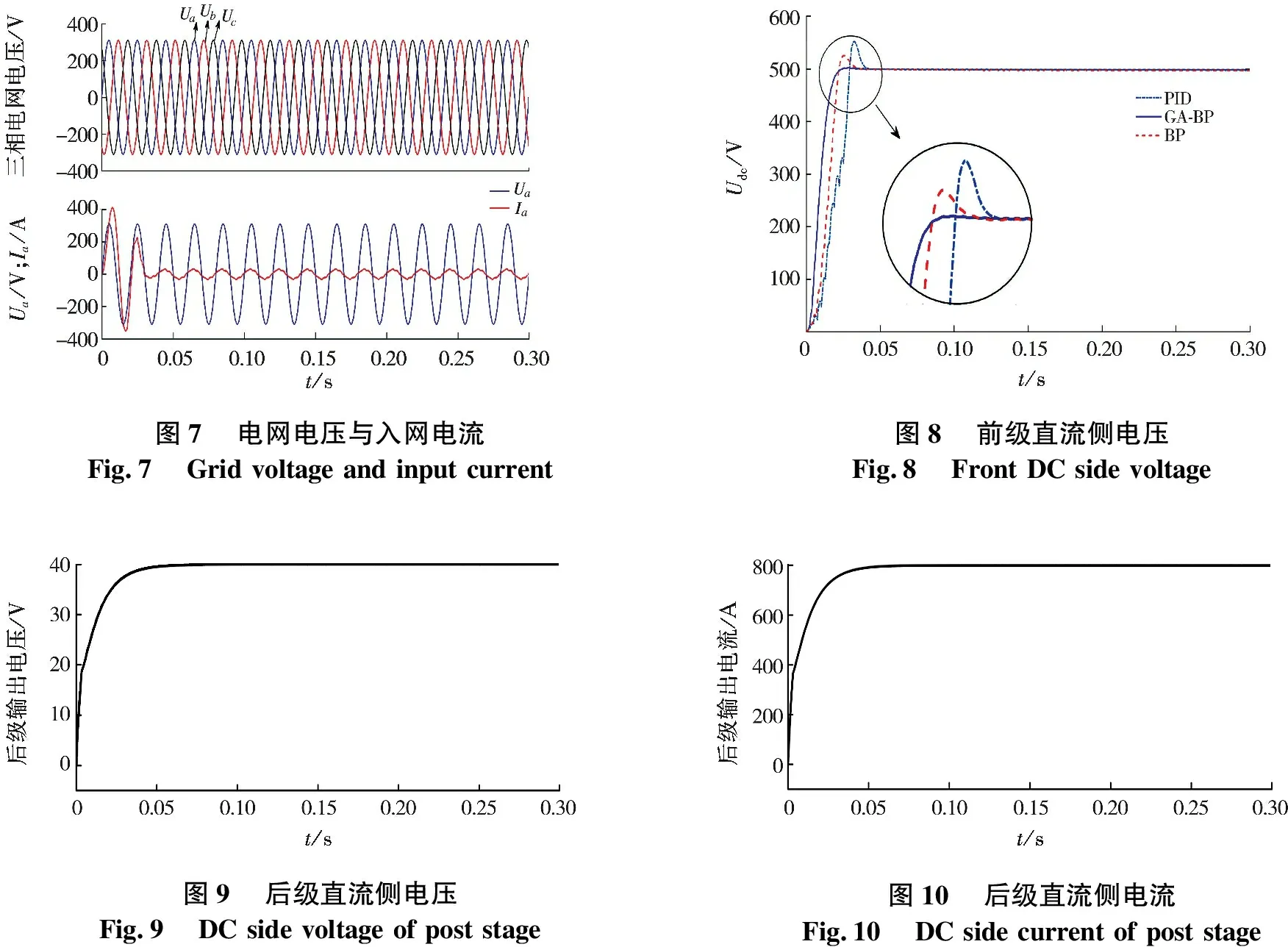
图7电网电压与入网电流Fig.7Grid voltage and input current图8前级直流侧电压Fig.8Front DC side voltage图9后级直流侧电压Fig.9DC side voltage of post stage图10后级直流侧电流Fig.10DC side current of post stage

由图7可知：在GA-BP控制下，入网三相电流波形为正弦波，并且电流与电压在0.03 s之内保持同相位，实现了功率因数单位化.由图8可知：在PID控制下，系统响应速度慢，超调量高，电压存在一定波动，稳定性差.相比PID控制，BP神经网络的控制使得直流侧电压在0.04 s左右达到稳态，系统响应速度快，超调量小.但在遗传算法优化BP神经网络(GA-BP)控制下，电解电源前级直流侧电压不仅可以与BP神经网络控制达到相同的效果，而且系统在0.03 s左右就达到稳态，整个控制过程无超调.由图9，10可知：在前级为后级提供稳定输入的情况下，电压、电流在很短的时间内就达到稳态，并且维持在40 V/800 A，从而可为电解槽提供稳定的电压和电流.

4 小 结

本文以电解碲电源为研究对象，将GA-BP优化算法应用到电解电源变换器中进行系统控制，分析了BP神经网络和GA-BP神经网络的控制原理，并通过MATLAB建模仿真验证了该方法的有效性.通过遗传算法的全局寻优和并行搜索能力优化BP神经网络的权值和阈值，进而调整电压环的PID参数，弥补了BP神经网络结构参数难以确定，收敛时间长，极易陷入局部最优的不足，实现了入网三相电流更好地跟踪电网电压，提高了电网的利用率，并且系统响应速度快、稳定性强，满足电解碲电源的要求.由于基于遗传算法优化BP神经网络的系统控制在BP神经网络控制的基础上增加了遗传算法，网络的训练速度变慢，所以，需要进一步进行研究.