基于LSTM的CFB机组SO2浓度模型

百嘎利 李彩霞 刘文慧 吴江 王伟 孔维政

摘 要：循环流化床机组（Circulating Fluidized Bed）脱硫塔SO2浓度与当前运行状况息息相关，但CFB机组是一个大惯性，大延迟，强耦合的对象，靠传统建模很难精确地对其生浓度进行建模。但脱硫塔入口SO2浓度不会产生突变，故在分析SO2浓度影响因素的条件下，利用对时间序列处理能力较强的LSTM算法，对SO2浓度进行建模，有望对运行人员提供科学参考，改善脱硫效率及成本。

关键词：CFB机组;SO2浓度;建模;LSTM算法

截至2018年，我国火力发电装机容量达到110495万千瓦，煤电装机占总装机容量的55%，达到98130万千瓦[1]。如此巨大的装机占比预示着未来很长一段时间内，我国发电的主力军依然是燃煤发电。

近年来，国家对环保要求愈发严格，导致许多火电机组污染物排放不能达标，因此大部分机组都在烟气尾部安装脱硫装置，以满足国家制定的污染物排放标准。最初我国循环流化床机组主要方式是炉内脱硫，但已很难达到排放标准。为了节省建设成本，循环流化床尾部脱硫装置往往容量有限，因此沿用了“炉内脱硫+炉外干湿法脱硫”的方式进行脱硫[2]，即在炉内通过石灰石脱硫将烟气SO2浓度控制在一定范围内，上限一般在1500mg/m3～3000mg/m3范围，再通过脱硫塔将SO2排放控制在超低排放的标准内。

但此方式存在诸多问题，最直观的问题之一就是脱硫塔入口SO2浓度测点常常存在误差，并偶尔会出现浓度计堵塞导致一定时间内SO2浓度不变的情况，影响运行人员操作石灰石给料机，最终可能引起短时间内SO2排放超标或者石灰石投入过量进而提高脱硫成本。若能建立起脱硫塔入口SO2生产模型，在测点出现问题时可以通过模型计算出脱硫塔入口SO2浓度大概范围，则可以避免这一现象。但循环流化床锅炉是一个大惯性，大延迟，强耦合的对象[3，4]，寻常机理建模较为困难。亟需一种新的方法来对此对象进行建模。

随着计算机发展，机器学习越来越多地运用在工业领域。本文通过RNN神经网络改进算法之一的LSTM（长短期记忆）算法对SO2生成模型进行建模，能大致计算出当前SO2浓度值，可为运行人员提供指导。

一、CFB机组炉侧SO2影响因素

这里以某330MW亚临界CFB机组为例。该机组主要通过炉外湿法脱硫，脱硫塔设计值在3000mg/m3，当脱硫塔入口在2500mg/m3以下时，炉内不喷石灰石且在脱硫塔入口SO2浓度3000mg/m3以上较短一段时间内，炉外脱硫的设计仍能将SO2排放值控制在超低排放标准内。

为简化SO2生产模型，在较短一段时间内，将煤质视为稳定，其含硫量变化不大，另外，由于炉内脱硫用的很少，截取的数据均为未用炉内脱硫的情况。

首先，SO2生成量与实际给煤量有关：

Vso2=kB-Vg

其中：VSO2——二氧化硫生成量;

B——燃烧的煤量;

k——煤中硫的质量分数;

Vg——未燃烧的固体硫。

这里存在的问题在于燃烧的煤量无法测算，但可以简化为瞬时给煤量的一阶延迟：

B=TBe-τs

其中：TB——瞬时给煤量;

τ——煤从给煤机到燃烧需要的时间。

图1为SO2浓度与给煤量之间的关系，采样时间为5s，时间长度为50min：

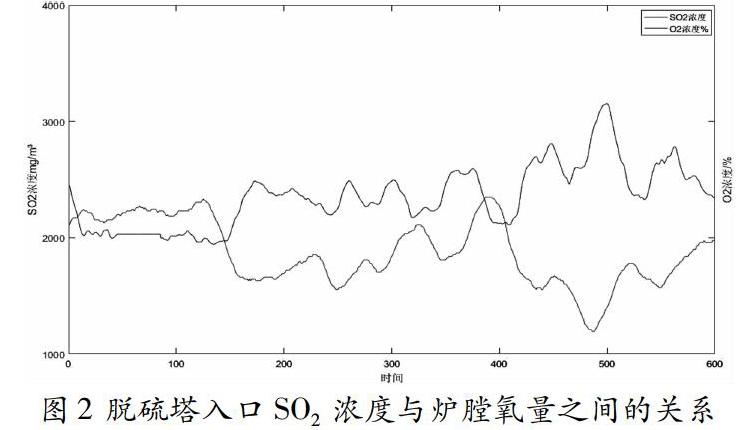
可以看到，虽然给煤越多，SO2生成量越多，但是生成的SO2浓度与给煤并无直接关系，这是因为SO2浓度是生成量与烟气流量的比值。但SO2生成与一二次风比值有关，在作为LSTM算法的输入量时为一次风量与二次风量。同时，一二次风量，给煤决定了氧量多少，氧量决定了炉膛内氧化还原性气氛，也是二氧化硫生成的关键。下图2为氧量与SO2浓度之间的关系，时间段与上图1相同。

这里可以很明显注意到，氧量变化趋势与SO2浓度变化趋势相反，且波峰波谷都超前SO2波谷波峰一段时间，因此，在LSTM算法输入量中，氧量是很重要的一部分。

最后，SO2浓度虽然与上述几个因素关系很大，但负荷是机组运行的基础，此外，根据SO2生成原理[5]，床温、床压[6]同样也不可忽视。

二、基于LSTM的CFB机组SO2浓度模型

（一）模型输入与输出

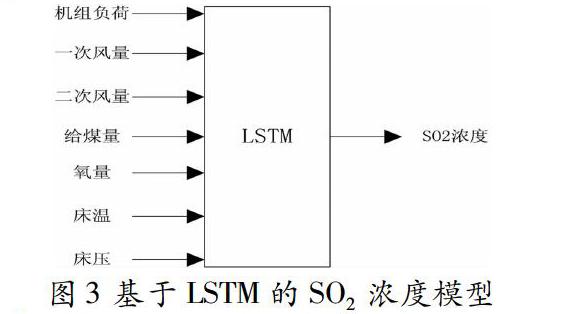
基于上述分析，将机组负荷，给煤量，一次风量，二次风量，氧量，床温，床压作为输入量，脱硫塔入口SO2浓度作为输出量，模型如下：

为保证模型精度，所有输入输出均在matlab中做归一化处理。

模型指标采用常用的均方根误差（RMSE）与平均百分比误差（MAPE）：

RMSE=1m∑mi=1（yi-yi）∧2

MAPE=∑mi=1yi-y∧yi×100m

（二）模型训练

训练集中含20000组输入输出数据，采样间隔为5S，时间长度约为28小时。LSTM模型中BATCH_SIZE为125，TIME_STEPS为160，两者相乘要与训练集的组数相同。输入量为7维，输出为1维，一层含10个神经元，学习速率为0.01，训练步长为1200。训练后，随机选取600个连续时间采样点（时间长度为50min）进行验证，算法运行环境为Spyder（Python 3.6）得到如下图形：

反归一化后，得到训练输出的SO2浓度值与实际值的图形如下：

模型值和实际值之间的均方根误差RMSE为143.34mg/m3，这对动辄3000mg/m3左右的脱硫塔入口來说，在接受范围之内。平均百分比误差MAPE为4.06，未超过5%。两个模型评价指标均证明了训练模型的正确性。

（三）模型泛化

为了证明模型的泛化能力，在训练集之外，需要另找数据进行模型运算，选取这些数据之前，需要用到之前一段时间的数据。比如，20000组数据的训练集，当我们对600组数据进行测试时，需要采20600组数据，前20000组作为训练，测试时，对第601组数据开始直到20600组数据均需要作为测试，但只有最后600组数据是在训练集之外的测试集。这是因为训练数据与测试数据维数需要保持一致，也是因为SO2浓度实际值跟前一时刻关系很大，其浓度不可能产生突变，这也是使用LSTM能够较好的利用好前一时刻的数据进行下一时刻数据建模的原因，此做法也能较好地提升模型正确性。在训练集之外，另外600点测试集的图形如下：