基于iTOUGH2的生物降解模型全局敏感性时变分析

杜建雯，施小清，徐红霞，吴吉春

(南京大学地球科学与工程学院/表生地球化学教育部重点试验室，江苏 南京 210023)

随着石油化工产业的迅速发展，大量石化液体产品在其贮存及运输过程中通过土壤进入地下水环境，这种化工产品多以非水相液体(Non-Aqueous Phase Liquids，简称NAPLs)的形式存在于地下水环境中，毒性大且难去除，对生态环境和人类健康造成巨大的威胁[1]。生物修复治理技术是地下水有机污染物治理方法之一，研究始于20世纪80年代，并不断发展[2]。其中原位生物修复技术是一种无需将地下水抽出，直接利用微生物好氧或厌氧降解有毒有机物的方法[3]，已被普遍认为是最具有发展潜力的地下水绿色修复技术，具有成本低，安全高效，无二次污染等优点[4]。

目前常采用Monod动力学方程[5-6]描述地下水中非水相有机污染物微生物降解过程。Monod模型考虑基质、电子受体以及营养物质对基质吸收率的共同影响，涉及参数较多，包括浓度、半饱和常数以及各种抑制因子[7]，因此基于观测数据反演参数存在较大的不确定性。采用敏感性分析可以识别出重要参数，降低参数估计维数，利于参数反演[8-14]。

敏感性分析包括局部敏感性分析[15]和全局敏感性分析[16-18]，已被广泛应用于水文地质和工程地质等多个领域[19-28]。局部敏感性分析方法基于响应变量对参数的局部导数评价敏感性，计算量较小，但易受参数的空间位置影响，且不能考虑参数间的相互作用。对于高度非线性、参数间存在相关性的复杂系统，会因没有考虑参数间的关联性而低估不确定性[29]。全局敏感性分析方法则相对具有更多优势，它在整个参数空间进行取样，可更加全面地反映参数变化对响应变量的影响，并且在参数间存在非线性和相互作用的情况下也可提供可靠的结果[15-18]。

目前常用的全局敏感性分析方法为Morris法[30]和Sobol’法[31]。前者对参数的相对敏感性大小进行评价，是一种定性分析方法；后者可量化评价各参数对输出不确定性的单独贡献以及共同影响。但Sobol’法较Morris法所需样本数量更多，通常先采用Morris法筛选出敏感性较高的参数，再采用Sobol’法进一步定量分析[12-14]。

然而，目前开展的敏感性分析一般只关注敏感性的一个整体平均情况和随空间的变化[8-13,19-25]，敏感性随时间变化研究较少[26-28]。但是分析不同时间段的敏感性情况，对全面识别参数敏感性，进而指导参数反演和决策优化都有着重要意义。例如，罗跃[26]等对不同变形阶段和参数区间的地面沉降模型参数进行全局敏感性分析，发现模型可在不同阶段分别进行参数反演；Bea等[27]通过分析反应运移模型参数的全局敏感性时空变化，更好地理解和评估了污染场地修复策略随时间的变化(即在修复的不同阶段可采用不同的修复策略)。此外研究敏感性在时间维度上的变化还可以帮助理解研究过程。例如，Valsala等[28]通过分析流量和吸附参数的敏感性随时间变化，揭示了微生物和胶体对含水层中溶解苯类组分浓度分布的影响过程。因此有必要开展敏感性随时间变化的研究，全面分析生物降解模型参数的敏感性，更好地理解生物降解过程并指导参数反演。

本文以甲苯好氧生物降解的一维砂柱试验为研究对象，基于TMVOCBio软件模拟生物降解过程。以砂柱右端甲苯浓度为响应变量，采用iTOUGH2[32]反演软件进行Morris法和Sobol’法全局敏感性时变分析。研究结果有助于深入理解Monod模型所描述的好氧生物降解过程，并为相关试验设计优化提供参考。

1 研究方法

1.1 概念模型

基于Macquarrie等[33]为理解地下水有机污染物生物降解过程开展的一维水平砂柱试验(图1)。

图1 一维砂柱好氧生物降解概念模型示意图Fig.1 Schematic diagram for conceptual model of the aerobic biodegradation in one-dimensional sand-column

假定在一个长为26 cm的砂柱中进行为期53 d的好氧生物降解试验，砂柱中初始微生物0.23 mg/L、氧气6 mg/L、甲苯0 mg/L，在砂柱左端以0.62 m/d的流速连续注入溶有甲苯(浓度为0.4 mg/L)和氧气(浓度为6 mg/L)的水溶液，在右端观测流出液中的甲苯浓度。

将该一维模型水平剖分为68个网格单元，除左右两端分别有2个、3个网格精细离散外，其余63个网格均离散为0.4 cm长。模型两端为第二类流量边界，相关参数值基于Macquarrie等[33]的砂柱试验参数设定(表1)。

表1 模型降解过程参数及试验条件参数取值[33]Table 1 Biodegradational and experimental parameters value

1.2 数学模型

基于TMVOCBio模拟试验过程，它采用改进的Monod动力学速率方程描述NAPLs生物降解过程[7]。考虑基质以及电子受体对基质吸收率的限制，包括浓度、半饱和常数以及各种抑制因子；忽略阻滞作用、生物相中的扩散、微生物迁移、微生物生长引起的孔隙度变化及其对介质渗透性的影响(堵塞)，并认为所有生物量都是有活性的[7]。

根据控制基质吸收率的限制因素，该方程有两种形式：(1)所有限制因素共同影响基质吸收率的多重Monod动力学方程；(2)只由主要限制因素控制基质吸收速率的最小Monod动力学方程[7]。假设所有限制因素共同影响基质的吸收率，即采用多重Monod动力学方程来描述生物降解反应：

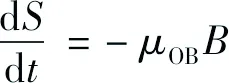
(1)

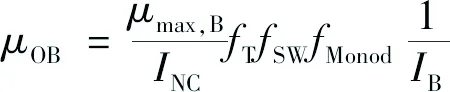
(2)

(3)

式中：S——基质浓度/(kg基质·(kg水)-1)；

t——时间/s；

B——生物量浓度/(kg生物量·(kg水)-1)；

μOB——单位基质利用率(按生物量计，/(kg基质·(kg生物量·s)-1))；

μmax,B——最大单位基质利用率(按生物量计，/(kg基质·(kg生物量·s)-1))；

INC——非竞争性抑制因子；

IB——生物量抑制因子；

fT——温度的抑制函数；

fSW——水饱和度的抑制函数(1或0)；

fMonod——Monod动力速率项；

S——基质浓度(kg基质/kg水)；

E——电子受体浓度(kg电子受体/kg水)；

IC——竞争抑制因子；

IH——Haldane毒性抑制因子；

KS,B——基质半饱和常数/(kg基质·(kg水)-1)，是生长率为最大生长率一半时的基质浓度；

KE,B——电子受体半饱和常数/(kg电子受体·(kg水)-1)，是生长率为最大生长率一半时的电子受体浓度。

1.3 全局敏感性分析方法

本文采用iTOUGH2反演软件进行Morris和Sobol’全局敏感性分析。iTOUGH2是美国劳伦斯Berkeley试验室开发的具有参数反演、全局敏感性分析和不确定性分析功能的软件，属TOUGH[34]家族系列软件，在国内外多相流逆问题领域已得到了广泛的应用[35-37]。相对而言，全局敏感性功能国内应用较少[29]。

1.3.1Morris法

Morris OAT(One-at-A-Time)法[17,27]是一个基于差分的全局敏感性分析方法，取样方法为一次只改变一个参数变量，主要用于定性识别和筛选较敏感的输入参数。假定对n个参数进行Morris敏感性分析，首先将n个参数空间[pi,min,pi,max]均分为(k-1)份，并将参数增量固定为Δi=Δ(pi,max-pi,min)，其中Δ=k/{2(k-1)}。然后从集合{0,1/(k-1),2/(k-1),…,1-Δ}中为每个参数随机选取一个辅助点ξi，代入pi=pi,min+ξi(pi,max-pi,min)中得到随机参数值pi并组成随机参数集p。每个随机参数集需进行(n+1)次敏感性运算，每次运算将依次随机变化一个参数pi为(pi+Δi)，计算该参数pi的“主效应”EEi：

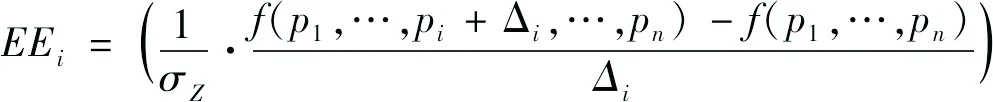
(4)

式中：f——响应函数；

P——n维随机参数集；

pi——第i个参数；

Δi——固定增量；

σz——比例因子，一般取观测值的标准差；

z——响应变量。

对于r个随机参数集来说，需根据式(4)进行r(n+1)次敏感性运算得到各参数的EES集合。再计算出三个统计量作为Morris敏感性指标：平均值(meanEE)，绝对值的平均值(mean |EE|)和标准差(SDEE)。其中meanEE和mean |EE|代表各参数在参数空间上的平均影响，视为全局敏感性指标；SDEE则用来识别非线性和相互作用效应(即参数间的相互作用对系统响应的影响)。

1.3.2Sobol’法

Sobol’法[17,28]是一种基于方差的全局敏感性分析方法，用于定量参数对系统响应的贡献度并分析相互作用效应。首先定义随机变量Z和随机向量P=[P1,P2,P3,…,Pn]，分别代表系统响应和参数组，Pi为参数组中的第i个参数。然后定义两个条件方差作为Sobol’敏感性指标，分别为一阶敏感性指数Si(Sobol’ Index)和总敏感性指数Sti(Sobol’ Total Sensitivity Index)。

一阶敏感性指数Si定义为:

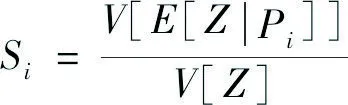
(5)

式中：E[·] ——均值；

V[·]——方差；

E[Z|Pi]——参数Pi单独变化引起的响应变量Z的平均变化。

Si量化了一阶效应，即参数Pi单一变化时对响应变量Z不确定度的贡献，不考虑相互作用效应。

总敏感性指数Sti定义为:

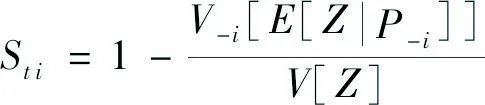
(6)

式中：E[·]——均值；

V[·]——方差；

E[Z|P-i]——除参数Pi外其余参数变化引起的响应变量Z的平均变化。

Sti计算了参数Pi及其与其他参数间的相互作用对响应变量Z的总效应。

通过分析Sti与Si差值的大小变化，可单独识别相互作用效应，即多个参数共同作用时对单个参数敏感性的影响[17]。相互作用效应越小，多参数的共同作用对单个参数的影响越小，越有利于对单个参数的反演识别。

2 结果分析

为理解好氧生物降解过程以及试验条件的影响，选取了降解过程参数和试验条件参数两类参数进行全局敏感性分析。采用Morris法探讨了降解过程参数和试验条件参数对模型输出结果的影响，然后使用Sobol’法定量分析了Morris法中敏感性较大的参数，并对参数间相互作用进行了分析。降解过程参数包括最大单位基质降解速率k、甲苯半饱和常数KS和氧气半饱和常数KE，由于采用Macquarrie试验[33]的反演估计值，故将不确定性范围设为15%[9]。试验条件参数包括水的注入速率rwat、甲苯的注入速率rtol和氧气的注入速率ro2，根据试验操作可能造成的偏差[33]，将不确定性范围设为20%。参数取值范围见表2。

2.1 Morris法分析结果

取砂柱右端甲苯浓度为响应变量，利用Morris法对表2中6个参数重复抽样120次，对获得的840组样点进行敏感性分析，分析结果如图2和图3所示。图2为Morris敏感性指标EE的标准差SDEE与绝对值均值mean |EE|的整体平均情况对比图。根据横轴mean |EE|得各参数敏感性排序为:rtol>rwat>k>KS>ro2>KE。根据纵轴SDEE得各参数相互作用效应排序为:rwat>rtol>k>KS>ro2>KE。

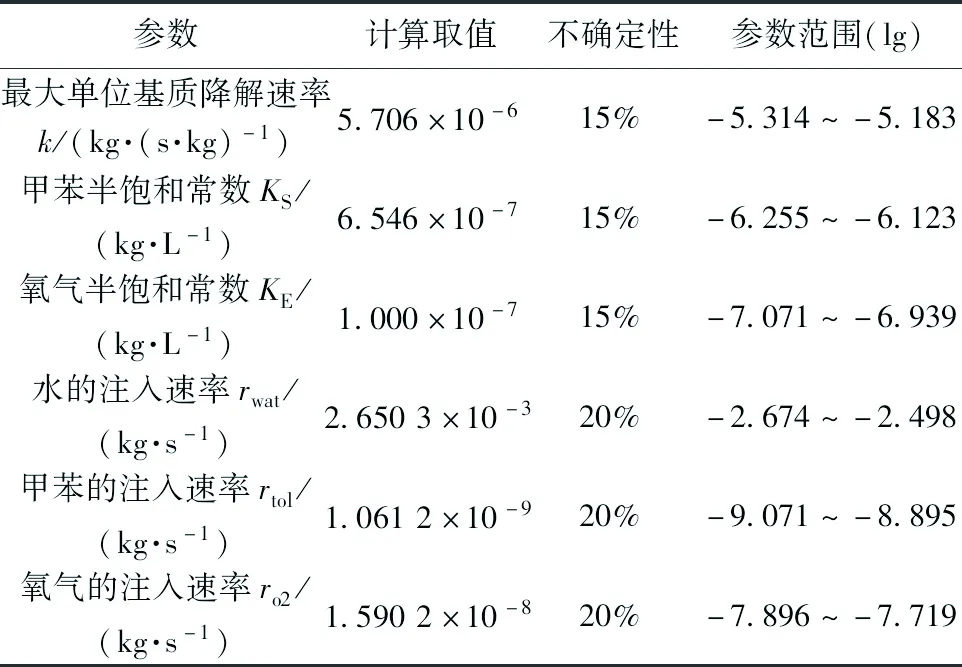
表2 全局敏感性分析的参数范围Table 2 Parameters range of global sensitivity analysis

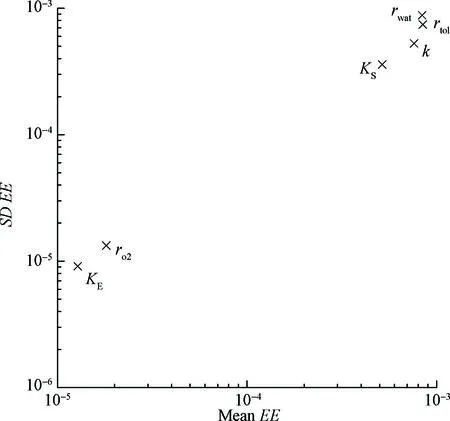
图2 Morris敏感性整体平均结果Fig.2 Average results of Morris sensitivity analysis

图3为同一响应变量下各参数的mean |EE|随时间变化曲线。从图3可以看出各参数的敏感性是随时间不断变化的，同时参数间的敏感性排序也随时间不断变化。试验早期敏感性排序为rtol>rwat>k>KS>ro2>KE，与Morris敏感性指标得到的结果一致。而试验晚期呈现出完全不同的顺序:k>KS>rwat>rtol>ro2>KE。说明传统的分析只比较某时刻或整体平均结果的敏感性(图2)，并不能代表整个试验过程的敏感性情况，故应展开敏感性随时间变化的研究，全面识别参数敏感性。

通过进一步分析参数敏感性时变曲线发现:(1)微生物好氧降解能力随时间变化先提高后减弱。由图3可知，降解过程参数k、KS和KE的敏感性随时间先逐渐增大后有所减小，即最初右端的甲苯浓度几乎不受降解过程参数的影响，故微生物降解开始进行；随着时间推移，降解过程参数对响应变量影响变大，即微生物不断降解甲苯；直至试验中期的某一时刻，降解过程参数对响应变量的影响达到最大，说明微生物降解能力达到最佳；再之后试验进入晚期，降解过程参数的影响程度开始减小，微生物降解逐渐衰弱。(2)该生物降解模型氧气充足。由于图3中氧气相关参数ro2和KE的敏感性在整个好氧降解过程中总是很小，即一个好氧生物降解试验几乎可以不受氧气影响，故认为试验中氧气充足。(3)试验晚期(敏感性较大的时间段)的数据更利于降解过程参数反演。从图3可看出，降解过程参数的敏感性直到试验晚期才达到最大，且之后逐渐减小，因此精确观测试验晚期数据更利于反演降解过程参数。(4)不同阶段试验条件控制标准可以不同。从图3试验条件参数rwat和rtol的敏感性变化发现，试验条件参数在早期敏感性较大，在试验中期和晚期相对较小，说明早期试验条件控制不当对于观测值的影响大于试验中期和晚期，因此早期的试验条件控制应严于试验中、晚期。

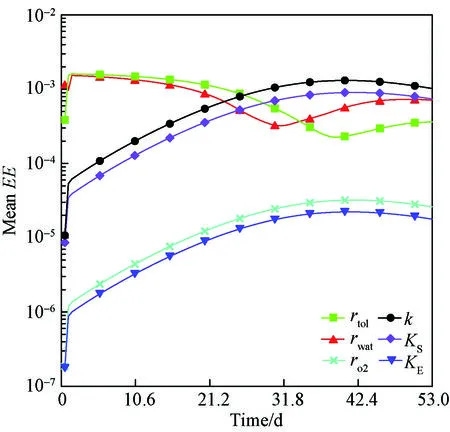
图3 Morris敏感性结果时变曲线Fig.3 Morris time-dependent sensitivity curves

2.2 Sobol’法分析结果

考虑到Morris法仅定性说明参数敏感性，故进一步采用Sobol’法定量参数对响应变量的相对贡献度，并分析参数间的相互作用效应。此处只针对前文Morris法中敏感性较大的参数即最大单位基质降解速率k、甲苯半饱和常数KS、水的注入速率rwat和甲苯的注入速率rtol进行Sobol’法敏感性分析，并仍以右端甲苯浓度为响应变量。Sobol’法中共选取2 500个样点，分析结果见图4。

图4为以右端甲苯浓度为响应变量时，模型部分参数的一阶敏感性指数Si(实线)与总敏感性指数Sti(虚线)随时间变化曲线。分析Si的变化趋势发现，参数的一阶敏感性排序情况(图4)与Morris分析结果(图3)基本一致。试验早期rwat与rtol对响应变量的贡献较大，贡献度分别约为45%和53%。试验晚期k的贡献最大，贡献度为49%～62%；KS的贡献次之，贡献度约在25%。

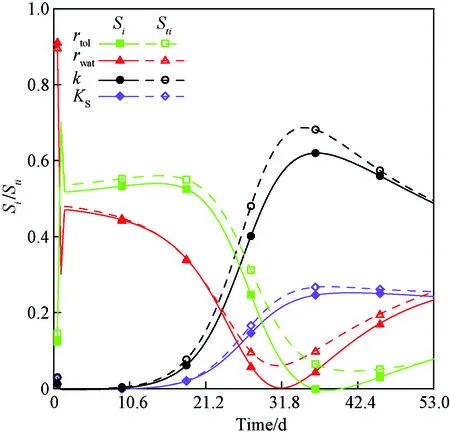
图4 模型降解过程参数的Sobol’敏感性指标时变曲线Fig.4 Sobol’ time-dependent sensitivity curves at main biodegradational parameters

对图4中各参数的Sti与Si的差值进行时变分析发现：(1)Sti在整个试验过程中均较Si略有增加，且Sti较Si的增加幅度随时间先增大后减小。即该试验过程中参数间存在相互作用，且该相互作用增大了参数单一变化时对响应变量的贡献。从图4中可以观察该相互作用效应随时间先增大后减小。其中，增加幅度变化最小的参数KS在试验早期和晚期的Sti较Si的增值近乎为0，在中期增大为2%；增加幅度变化最大的参数k在试验早期和晚期的增值同样约为0，在中期则达6%。(2)试验早期和晚期的数据更利于降解过程参数反演。这是由于相互作用效应随试验先增大后减小，选择相互作用效应相对较小的试验早期和晚期更利于参数反演。同时可以根据图4对相互作用效应排序进行时变分析，将比图2的SDEE的整体平均排序更能反映实际情况。

3 结论与展望

为深入理解好氧生物降解过程以及试验条件的影响，本文以一个好氧生物降解甲苯的一维砂柱试验为例，采用iTOUGH2反演软件中的Morris法和Sobol’法，以砂柱右端甲苯浓度为响应变量，分析了模型降解过程参数和试验条件参数两类参数的全局敏感性。其中降解过程参数包括最大单位基质降解速率k、甲苯半饱和常数KS和氧气半饱和常数KE。试验条件参数包括水的注入速率rwat、甲苯的注入速率rtol和氧气的注入速率ro2。研究表明：

(1)基于iTOUGH2进行全局敏感性分析可得到参数敏感性随时间变化曲线，有助于理解研究过程。对于好氧生物降解模型，敏感性排序随时间发生变化，早期试验条件参数敏感性较大(一阶敏感性均多于40%)，排序为rtol>rwat>k>KS>ro2>KE；晚期降解过程参数敏感性较大(k的一阶敏感性为49%～62%)，排序为k>KS>rwat>rtol>ro2>KE。这是因为好氧生物降解能力随时间先逐渐增大而后又稍有减小，从而导致降解过程参数的敏感性较试验条件参数由大变小。同时参数间相互作用效应也随时间发生变化，本例表现为参数间的相互作用增大了参数单一变化时的影响，且该相互作用效应随时间先增大后减小。

(2)根据全局敏感性时变分析可识别出试验过程中参数敏感性较大且相互作用效应较小的时段，采用此阶段的试验数据更有利于参数反演。对于本例，试验晚期的数据较其他时段更利于降解过程参数的反演估算。同时为避免试验条件控制不当导致观测数据误差增大，试验条件的早期控制应严于试验中、晚期。后续可继续在iTOUGH2框架上进行数据价值分析，可帮助敏感性分析更精准的指导试验设计和反演求参。