次分数跳-扩散过程下后定选择权定价

王瑞,薛红,梁喜珠

（西安工程大学理学院,陕西西安710600）

1973年,Black和Scholes开创性地提出了Black-Scholes模型[1],随后该模型广泛运用于各种期权定价问题中.然而研究表明,Black-Scholes模型中的假设并不适用于收益率为非独立、非线性的金融市场[2-4].后来,一些学者用分数布朗运动来描述与过去价格相关的股价的变动,其具有自相似性和长程依赖性[5-8].

随着布朗运动的推广,2004年Bojdecki等[9]提出了次分数布朗运动,它在保持分数布朗运动的一些性质的同时还具有增量非平稳性,用其描述现实中的股价市场变化更为合理,对次分数布朗运动的详细定义见文献[10-11].2014年,肖炜麟等[12]研究了次分数布朗运动环境下带交易费用的备兑权证的定价,更加说明了次分数布朗运动可以更好地描述一般的金融市场.但由于实际金融市场中的股票价格会出现波动或跳跃的情形,故2019年,王佳宁等[13]在次分数跳-扩散过程下建立了金融市场定价模型,对最值收益期权的定价问题进行了深入研究.

投资者在选购股票时,并不能确定其价格在将来会上升还是下降,因此投资者在投资过程中存在的风险比较大,而后定选择权[14]能很好地解决这一问题,持有人可以在该期权合约到期前某一确定时间点选择其为看涨或看跌期权的奇异期权.近几年,毕学慧等[15]和詹颖心等[16]分别推导了几何布朗运动下简单后定选择权和分数布朗运动下复杂后定选择权的定价公式.2012年,黄开元[17]在股票价格服从于分数布朗运动的基本假设下,得到了利率满足Hull-White模型的后定选择权保险精算定价公式.本文对次分数跳-扩散过程下后定选择权定价问题和方法进行了研究.首先通过推导得出欧式看涨、看跌期权的定价公式,从而得出其平价关系,然后运用保险精算方法给出后定选择权的定价公式,最后通过Matlab软件给出数值算例并进行分析.

1 次分数跳-扩散过程下金融市场数学模型

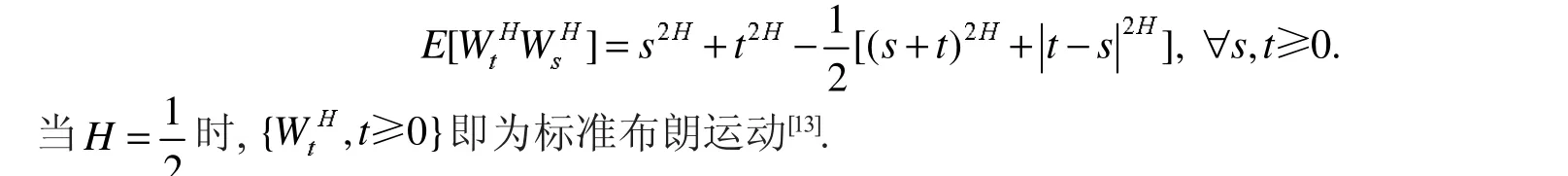
假设股票价格St满足随机微分方程

引理1随机微分方程（1）的解为

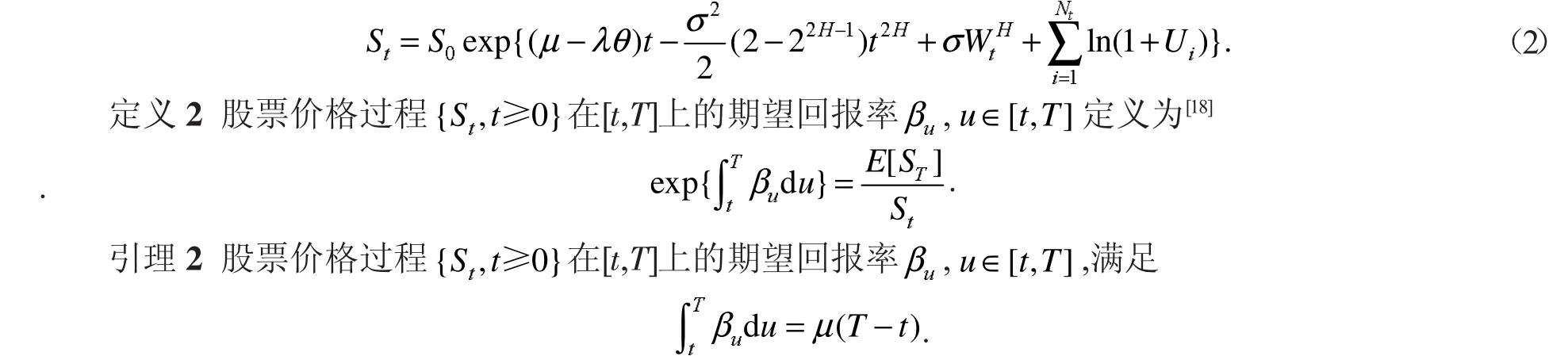
2 欧式期权定价

定义3欧式看涨期权在t时刻的保险精算价格定义[19]为

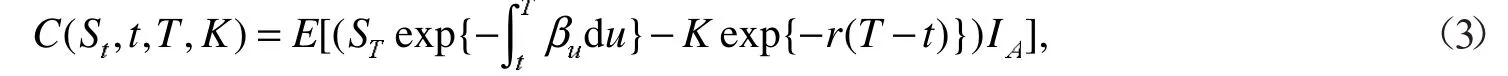
欧式看跌期权在t时刻的保险精算价格定义为

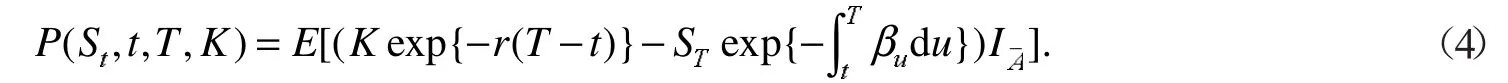
式（4）中：参数K、T、r分别表示该期权的执行价格、到期日与无风险收益率,I为示性函数, A是A的补集,且

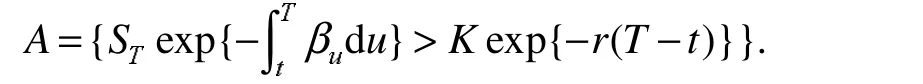
定理1欧式看涨期权在t时刻的保险精算价格

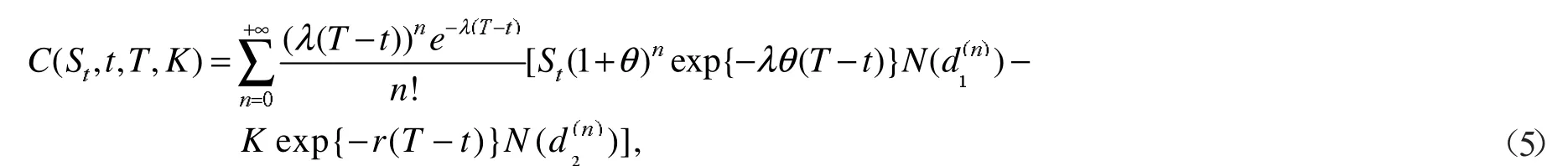
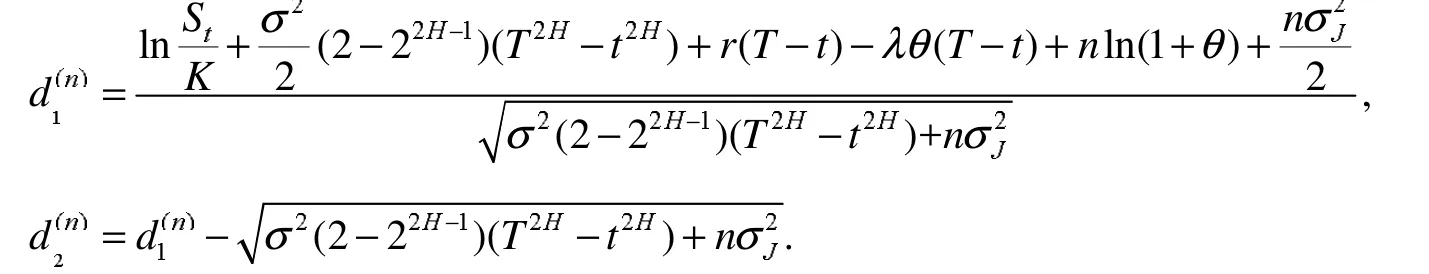
证明：由定义3有

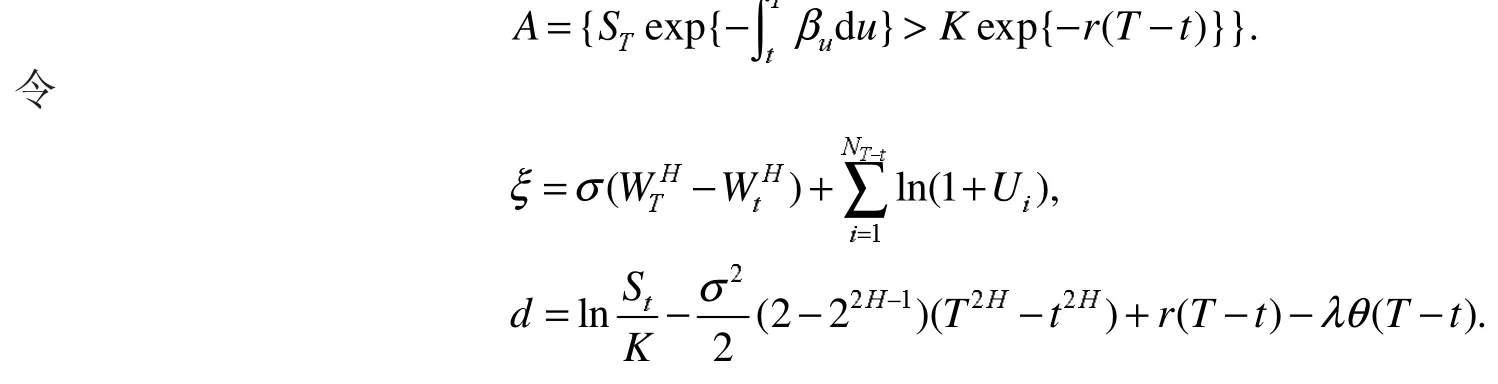
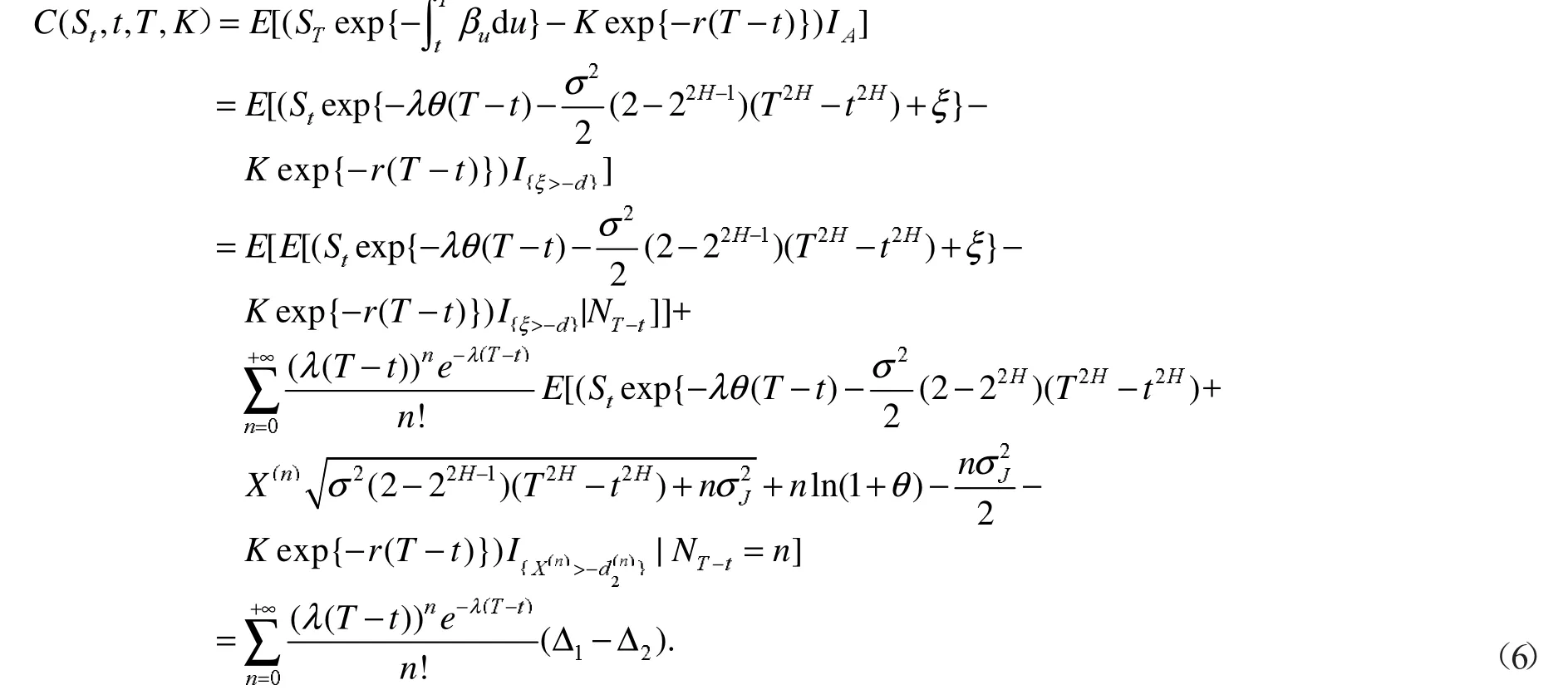
式（6）中

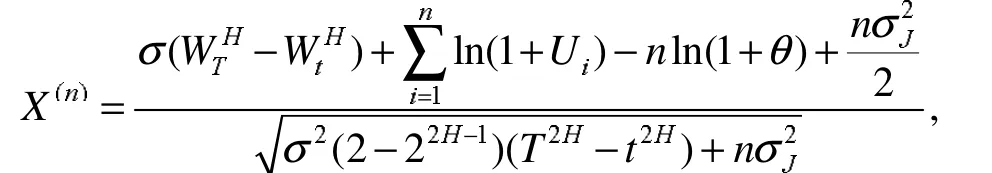
且 X(n)～N（0,1）,同时

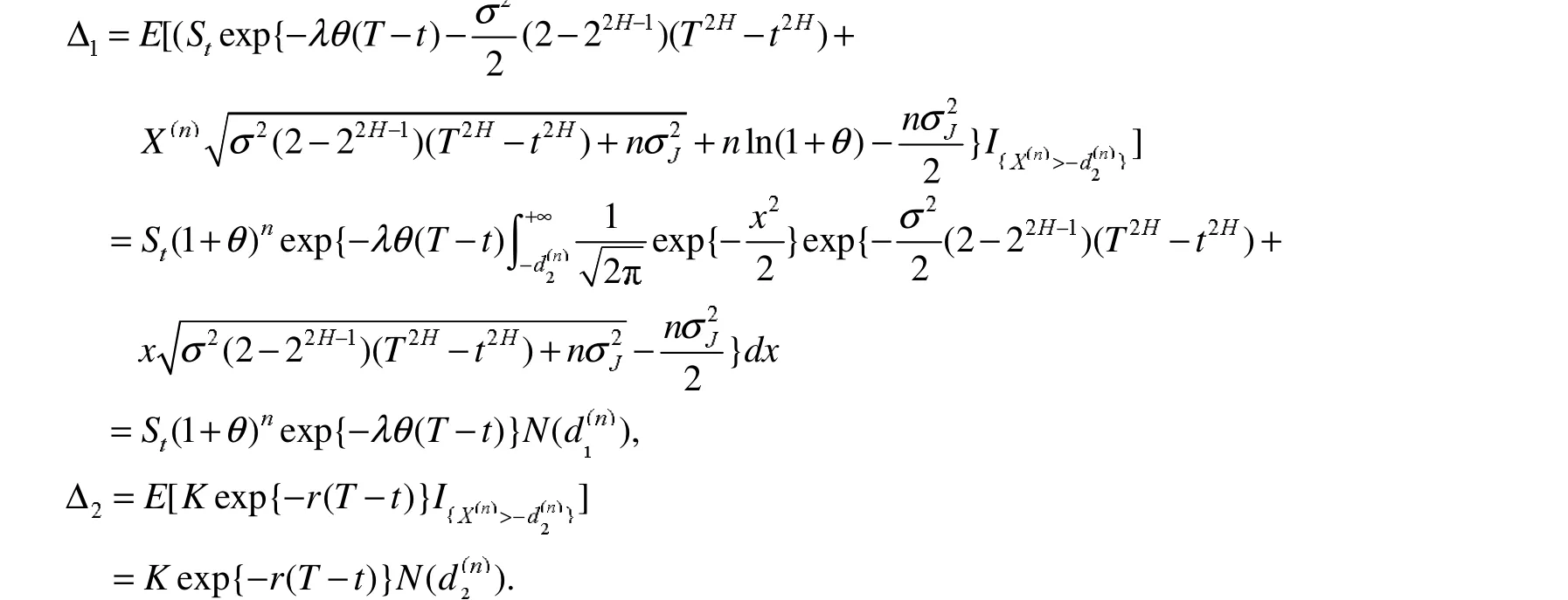
定理得证.

定理2欧式看跌期权在t时刻的保险精算价格

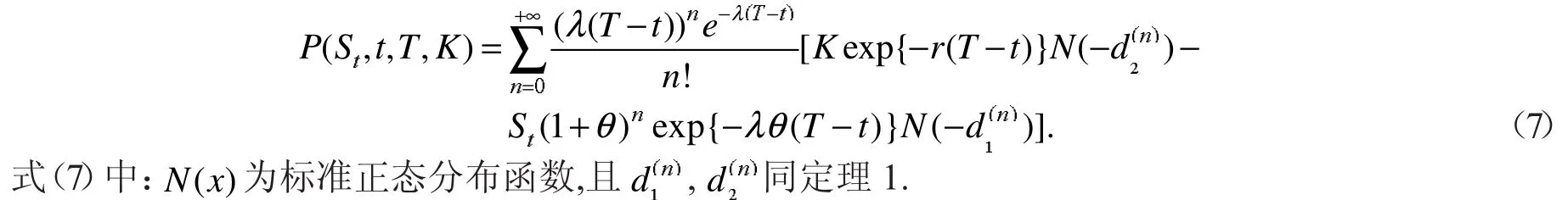
证明：类似定理1可证.

推论2欧式看涨、看跌期权的平价关系式为

3 后定选择权定价

定义4到期日为T,执行价格为K,在到期前某一择选点t*（t*＜T）选择看涨、看跌的后定选择权,其在t*时刻的现金流量[14]为

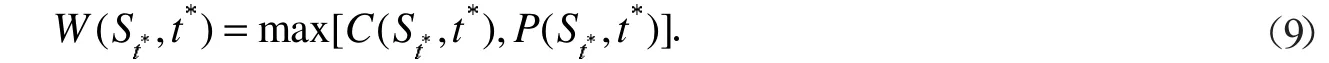
式（9）中：C（St*,t*）和P（St*,t*）分别表示标准欧式看涨和看跌期权在时刻t*的保险精算价格.

由看涨、看跌期权的平价关系可得后定选择权在时刻t*的现金流量为

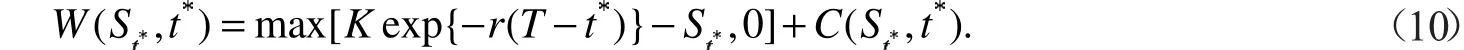
定理3到期日为T,执行价格为K,在到期前某一择选点t*（t*＜T）选择看涨、看跌的后定选择权,其在t*前任意时刻t（0＜t＜t*）的保险精算价格

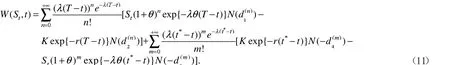
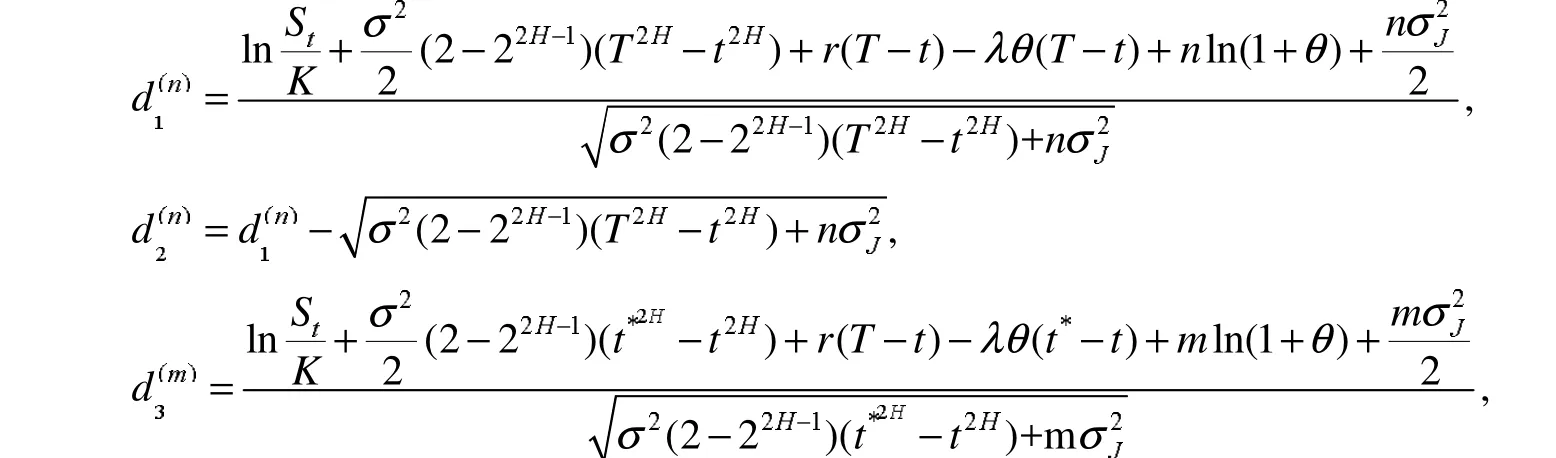
证明：令

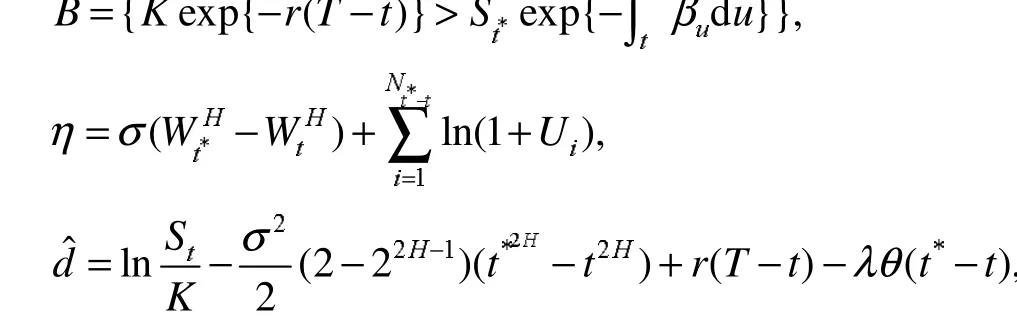
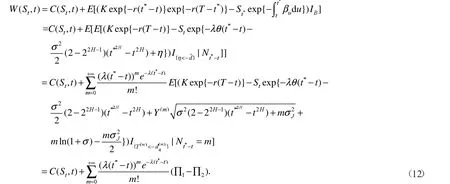
式（12）中

从而定理得证.

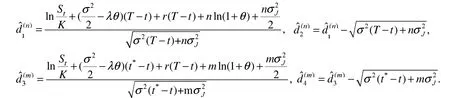
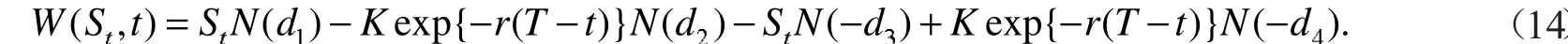
4 数值算例及分析

在到期日前某一择选点t*时刻选择看涨或看跌期权的后定选择权价格公式已由定理3给出,根据该定价公式,运用Matlab软件给出数值算例并进行分析.现假设该后定选择权以股票为标的资产,并且该股票价格满足次分数跳-扩散过程式（1）.假设模型中各参数取值如下：

K=90,T=0.5,t=0.3,t*=0.45,r=0.05,n=30,m=30,λ=4,σ=0.2.

在其他定价参数不变的情况下,分别改变Hurst指数H和跳跃强度λ的取值,观察并分析在不同的股票价格S下后定选择权价格W的变化情况,见表1、表2.

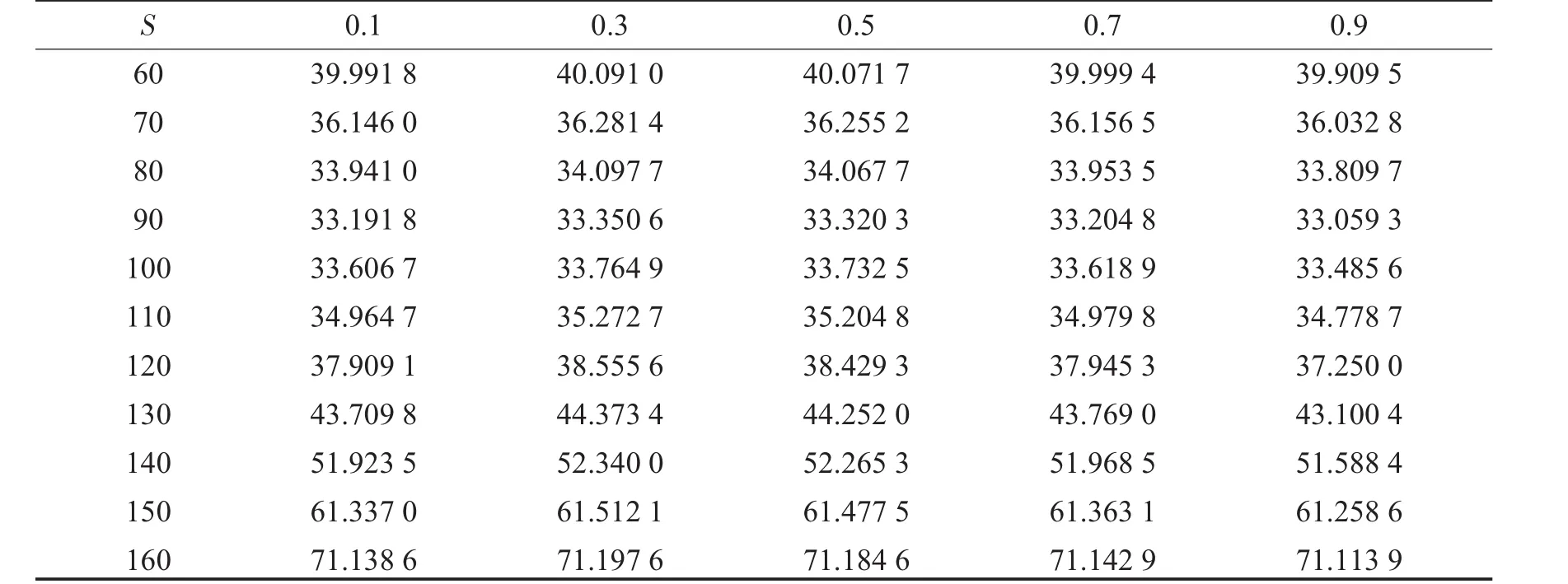
表1 股票价格和参数H取不同值的后定选择权价格Tab.1 Chooser option price when stock price and parameter H take different values

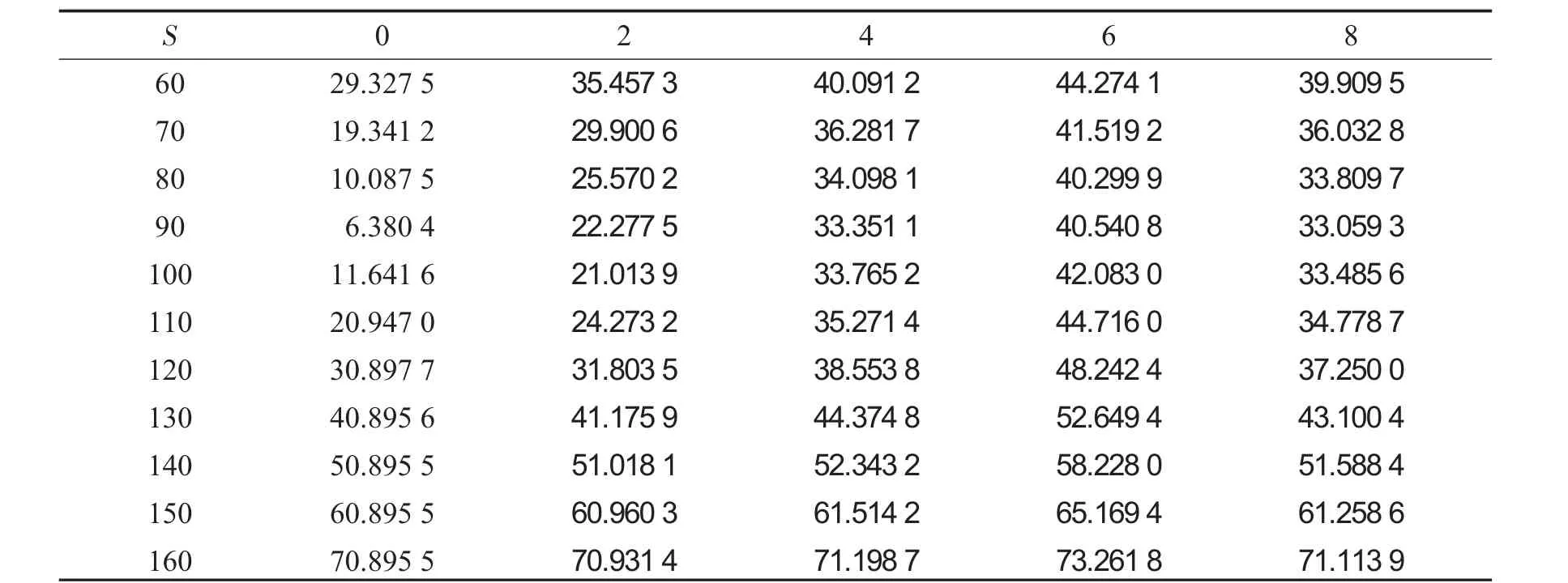
表2 股票价格和参数λ取不同值的后定选择权价格Tab.2 Chooser option price when stock price and parameterλtake different values

根据统计表1与统计表2中的数据分别绘制出相应的折线统计图.图1表示股票价格和参数H取不同值时,后定选择权价格的变化.

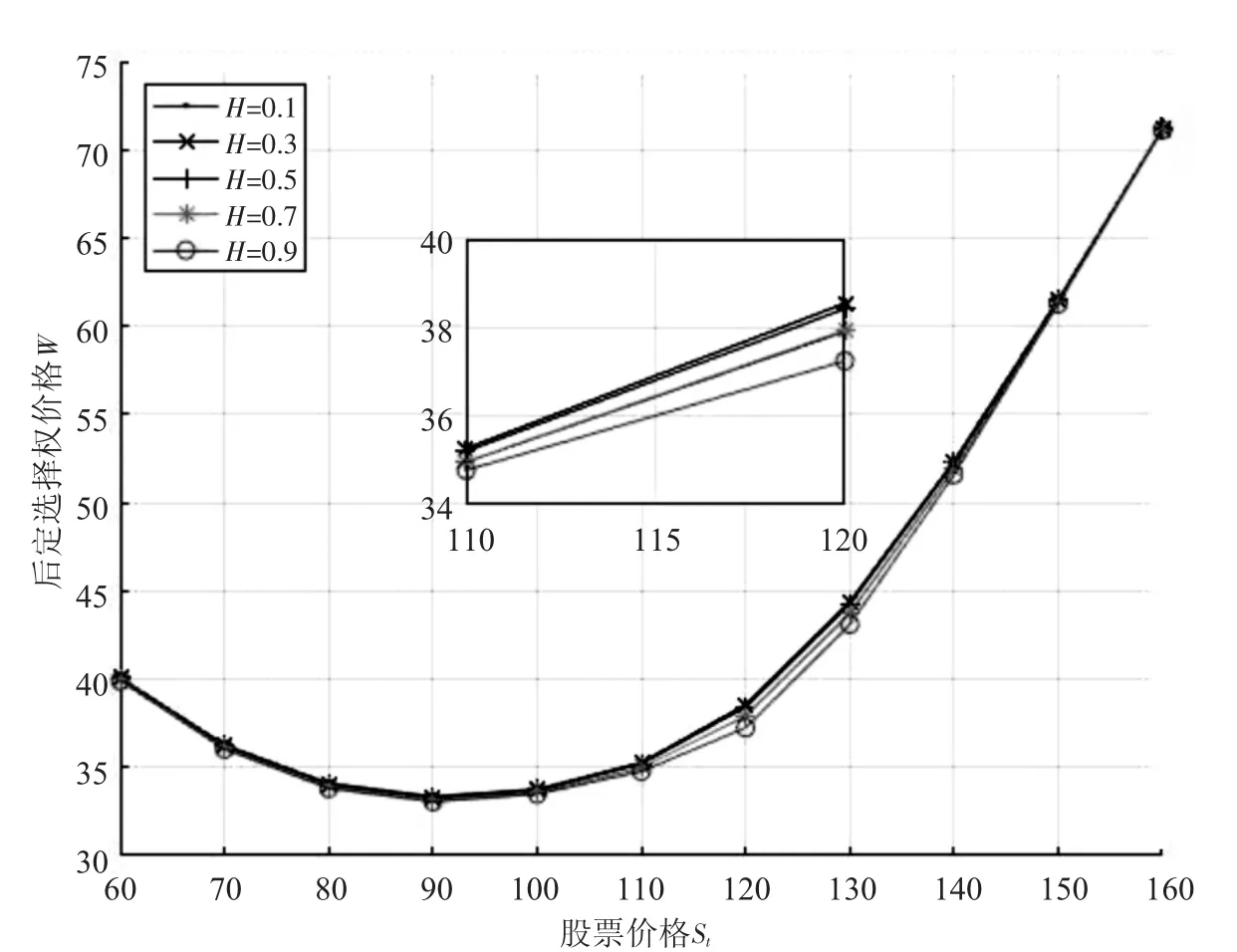
图1 对应不同参数H的后定选择权价格Fig.1 Chooser option price corresponding to different parameter H

由图1可知,后定选择权价格随着Hurst指数H的改变而改变,即金融市场不同的分形结构,对期权价格有显著性影响.当0.1≤H＜0.3时,后定选择权价格与参数H呈同方向变化,而当0.3≤H＜0.9时,后定选择权价格与参数H呈反方向变化,并且当参数H取值0.3与0.5时,后定选择权的价格极其接近.而在参数H一定的情况下,后定选择权价格随着标的资产价格与执行价格的接近而降低.

图2表示股票价格和参数λ取不同值时,后定选择权价格的变化.

图2 对应不同参数λ的后定选择权价格Fig.2 Chooser option price corresponding to different parameterλ

由图2可知,跳跃强度与后定选择权价格成正比例关系,即后定选择权的价格随着实际金融市场中跳跃情形的严重而增高.当固定跳跃强度时,标的资产价格越接近执行价格,对应的后定选择权的价格也越低.

5 小结

本文综合考虑了实际金融市场中股价收益率变化非平稳与股票价格会发生波动或跳跃的这两种情形,将次分数布朗运动与带有跳的Poisson过程引入到奇异期权定价问题中,对次分数跳-扩散过程下后定选择权的定价问题进行了探讨,通过保险精算方法推导出其定价公式,并且给出相应的数值算例,通过分析可知,在固定其他参数取值的情况下,后定选择权的价格随着Hurst参数与波动强度的改变而改变.