基于迁移局部线性编码的跨域图像表示方法

孟欠欠,沈龙凤,李晓,胡贺军

（淮北师范大学计算机科学与技术学院,安徽淮北235000）

图像分类是计算机应用研究领域的一项基础研究,广泛应用于现实生活中,如图像检索、视频监控及疾病类别诊断等,具有重要的研究价值.对图像表示方法的研究首先是基于低层特征的研究,如利用方向梯度直方图（HOG）提取图像的纹理特征[1],局部不变特征转换（SIFT）提取局部特征[2],以及加速稳健特征（SURF）方法进一步学习局部描述子等[3].低层特征虽然分辨率更高,包含更多位置、细节信息,但其语义性更低,噪声更多,很难高效地表示图像.图像的高层特征具有更强的语义信息,因而很多机器学习方法用图像的高层表示,解决图像分类问题.稀疏编码作为一种经典的图像表示方法,能提取图像的高层特征,提高量化准确率[4].Gao等[5]提出的拉普拉斯编码（LSC）在稀疏编码基础上引入拉普拉斯项,有效改善了编码的不稳定性.Zheng等[6]将其扩展为图正则化稀疏编码（GSC）,保留了图像特征的相似性.Long等[7]首次把迁移学习引入稀疏编码,提出迁移稀疏编码（TSC）,挖掘域间共同特征,解决了跨域分类问题.以上编码方法不断改进,形成了成熟的特征表示方法.然而,在对图像进行分类时,同类图像在不同拍摄环境中,图像内容变化较大,学习的特征分布也不同,利用传统的编码方法学习编码,得到的编码无法抓取形态或定位对象,因而需要提取合适的局部特征表示图像.K均值聚类[8]是比较经典的局部特征提取方法,该方法主要通过K近邻学习的方法实现对图像局部特征的编码,取得较好的分类效果.为更进一步提高分类准确率,很多研究学者将传统特征编码方法与编码的局部性约束相结合,如Yu等[9]认为局部性比稀疏性更重要,提出局部坐标编码（LCC）；Wang等[10]将稀疏编码与局部约束项相结合,提出局部线性编码（LLC）,不仅能保证编码稀疏性还能保证重构误差最小化；Min等[11]在LLC基础上加入拉普拉斯正则化项,提出基于拉普拉斯正则化项的局部线性编码算法（LapLLC）,进一步保证了编码的鲁棒性.然而以上方法需要源域与目标域数据服从同一特征分布,无法处理跨域分类问题.基于此,本文将迁移稀疏编码与局部约束项相结合,提出一种迁移局部线性编码的跨域图像表示方法.通过K均值聚类学习初始字典基,利用图拉普拉斯正则化项保留数据集的几何特征,同时考虑源域与目标域的特征差异,实现源域到目标域的迁移性学习,解决跨域图像分类问题.此外,方法利用局部约束项最小化特征的重构编码,使学习的编码更具有局部平滑性和特征重构性,提高了跨域分类效率.

1 相关理论

传统稀疏编码主要由过完备字典基和编码系数组成,虽然能够提高量化的准确率,却忽略了特征之间的局部信息.为进一步提取图像的稀疏性局部特征,局部线性编码将局部约束项引入到稀疏编码特征公式中,最终目标模型为

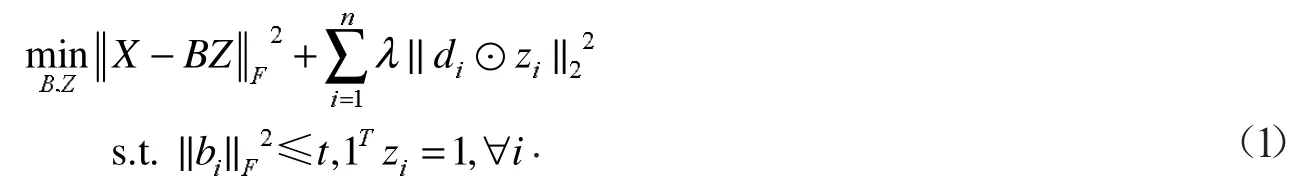
考虑到LLC编码过程中没有考虑图像本身的几何特征,相似的特征有可能会被编码成不同的码字,导致编码不稳定.为进一步保证编码的稳定性,LapLLC在LLC基础上引入拉普拉斯正则化项,以保证编码的一致性.其目标模型为

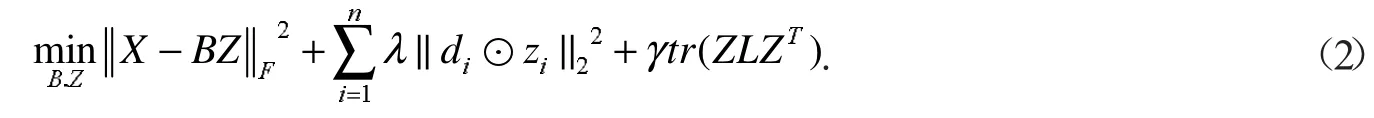
式（2）中：tr（ZLZT）为拉普拉斯正则化项,γ为拉普拉斯参数,L为拉普拉斯矩阵,通过计算样本局部特征的列差加权平方和来表示数据集的相似度,其计算公式为

式（3）中：W为样本数据集的权值矩阵,D为度矩阵,且L=D-W.局部线性编码和基于拉普拉斯正则化项的稀疏编码均考虑了图像特征的局部信息,在处理图像分类时取得较好的量化效果.

然而,当源域数据与目标域数据不服从同一特征分布时,会极大影响跨域图像的分类精度,为进一步解决该问题,学习更鲁棒性和局部性的编码特征,本文将迁移稀疏编码与局部约束项相结合,在保留编码局部性同时解决跨域分类问题.可以得到基于迁移局部线性约束编码的图像表示数学模型为

式（4）中：μ为均值差参数,tr（ZMZT）为最大均值差项,可用于实现源域到目标域的特征迁移,本文采用源域与目标域的一阶矩差值进行计算,公式为

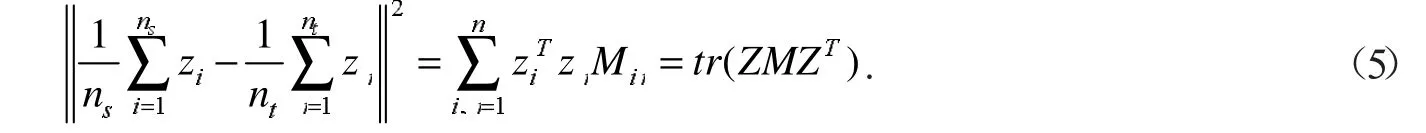
式（5）中：M为数据域间距离,也称之为最大均值差,有

本文模型主要包括两个正则化项和一个局部约束项,其中拉普拉斯正则化项和最大均值差正则化项,分别用于保留数据集的几何特征以及实现源域到目标域的迁移性学习；而局部约束项,则用于保证编码的局部平滑性和特征重构性.

2 基于迁移局部线性编码的图像表示方法

2.1 算法流程

本文方法为保证编码的局部性以及解决数据域特征分布不一致问题,将局部约束项和迁移稀疏编码相结合,保证相似编码局部平滑性和缩小数据域分布差异,使数据域样本保留各自的内部属性,较好地解决了跨域图像分类问题.先通过K均值聚类方法学习簇心个数为k的字典B0,然后将目标模型转化为如下两个子问题的求解：编码系数优化与字典优化,直至目标函数收敛.算法流程图见图1.

图1 LMLLC算法流程Fig.1 The algorithm flowchart of LMLLC

2.2 编码系数优化

学习初始字典基后,为更新编码系数,需要固定字典B,最优化编码Z,目标函数转化为线性最小二乘优化问题,利用特征符号搜索算法求解,优化模型为

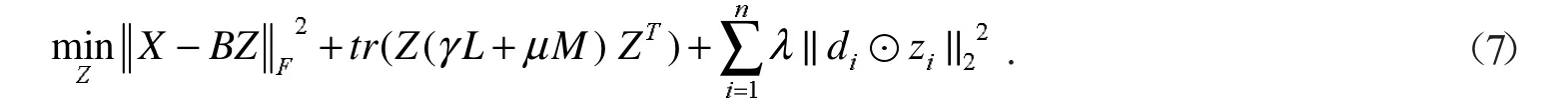
假定xi为单个样本点,zi为每个样本点的待编码特征,此时目标模型公式（7）可改为

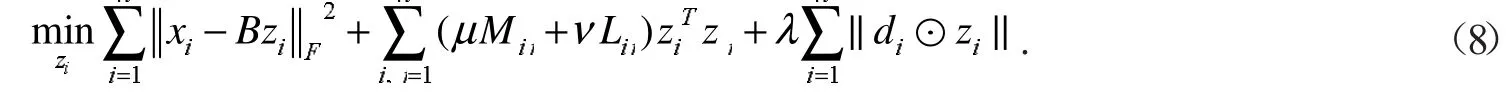
因仅考虑待编码特征zi的最优化问题,为求解方便,同时避免梯度下降时函数不收敛,将公式（9）转化为

2.3 字典基优化

字典优化问题等价等价于固定编码A,相应的优化模型转化为

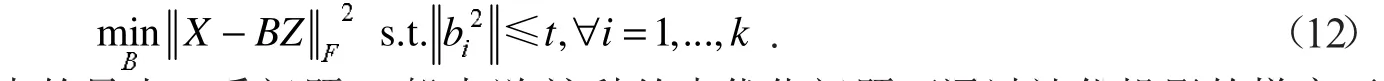
式（12）是一个带二次约束的最小二乘问题.一般来说,这种约束优化问题可通过迭代投影的梯度下降法解决.为更有效求解,根据文献[4]将式（12）转化为拉格朗日对偶问题,得到

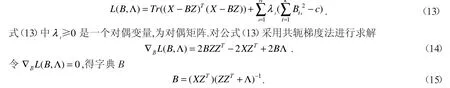
3 实验验证

3.1 实验数据集及实验设置

首先介绍5个标准的图像数据集,包括Amazon、Caltech-256、Webcam、USPS和MNIST等数据集[12].其中Amazon包含958幅图像,Caltech包含1 123幅图像,Webcam包含295幅图像,实验在3个数据集中随机抽取10类,把每幅图像表示成800维向量.从MNIST数据集和USPS数据集中随机抽取2 000和1 800幅图像,共10类,把每幅图像表示为256维的向量.通过处理共定义3个跨域分类任务：Amazon vs Caltech、Amazon vs Webcam和USPS vs MNIST,本文实验主要在这3个跨域图像数据集上进行.每个分类任务中前者作为有标记训练集,后者作为无标记测试集.

本文所提的迁移局部约束线性编码方法主要包括两个过程：字典优化和编码优化,两者交替迭代直至目标模型收敛.对于字典的优化学习,利用K均值聚类学习初始字典基,此时设置簇心个数K=128,即固定字典的尺寸为128；在编码优化模型中的涉及的3个参数μ,γ,λ统一设置为μ=1×105,γ=1,λ=0.01；对于实验迭代次数NT,将其值NT=10.在对比实验选择中,将本文提出的方法与LR方法、PCA方法、SC方法、GSC方法、TSC方法、LLC方法和LapLLC方法等6种经典的图像表示方法进行对比,并将平均分类精度作为评价标准,实验结果如表1所示.

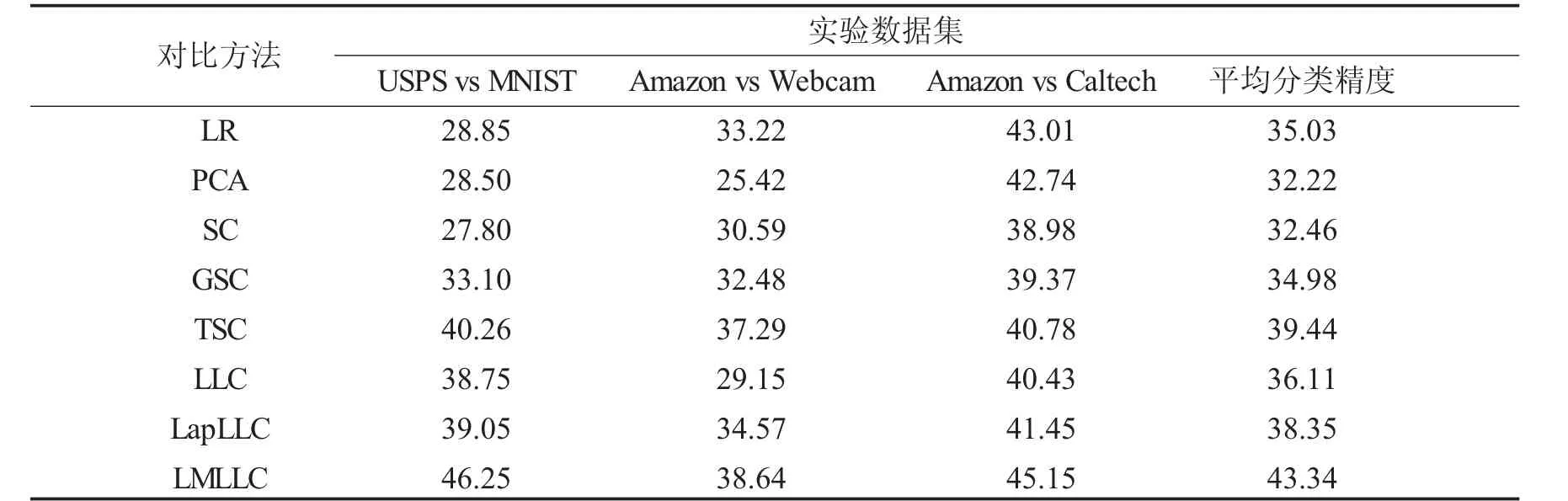
表1 平均分类精度Tab.1 The average classification accuracy %

3.2 实验结果分析

与传统编码方法仅考虑图像的稀疏性不同,本文方法主要考虑编码的局部性,由表1中可以看出,LLC方法比SC的平均分类精度高3.65个百分点,LapLLC比GSC高出3.37个百分点,均表明编码的局部性比稀疏性更重要.究其原因,编码的局部性不仅能保证稀疏性,亦能保证编码的局部平滑性,生成的图像表示更具代表性.为了验证拉普拉斯正则化项对分类精度影响,在表1中,GSC的平均分类精度比SC的平均分类精度高2.52个百分点,而LapLLC比LLC高出2.24个百分点,都表明图拉普拉斯正则化项重要意义,该正则化项能保留数据集的几何内蕴结构,一定程度上改善改善了编码的不稳定性,从而提高了图像的分类精度.此外,TSC和LMLLC的平均分类精度比GSC和LapLLC分别高4.56个百分点和4.99个百分点,主要因为最大均值差项能实现源域到目标域的迁移学习,解决数据域特征分布不一致的问题,从而有效提高跨域分类精度.

在3个跨域图像数据集上,本文提出的LMLLC方法的平均分类精度比其他6种对比方法的分类精度高.分析其原因,本文LMLLC方法中既考虑了域间分布差异和图像几何特征,又引入了局部线性约束,使学习的编码具有局部平滑性和更强的鲁棒性,最终提高了跨域图像分类精度.

3.3 参数分析

为进一步验证图拉普拉斯参数γ、迁移性参数μ和局部性参数λ对跨域分类精度的影响,本文对这3个参数分别取不同值并记录其对图像分类精度的影响,如图2至图4所示.为验证迭代次数对目标函数的收敛度的影响,取NT=20,观察其对目标函数的影响,如图5所示.

对于图正则化参数 γ,设置 K=128,μ=1×105,λ=0.01,将 γ 分别取 0、0.01、0.1、1、10 和 100,观察其分类精度对分类效果的影响,结果如图2所示.可以看到在γ取[0.1,1]时分类效果较好,而在取＜0.1或＞10的值时效果较差,主要是因为图正则化参数用于控制图像的几何特征,γ过小或过大均会影响图像的分类精度.

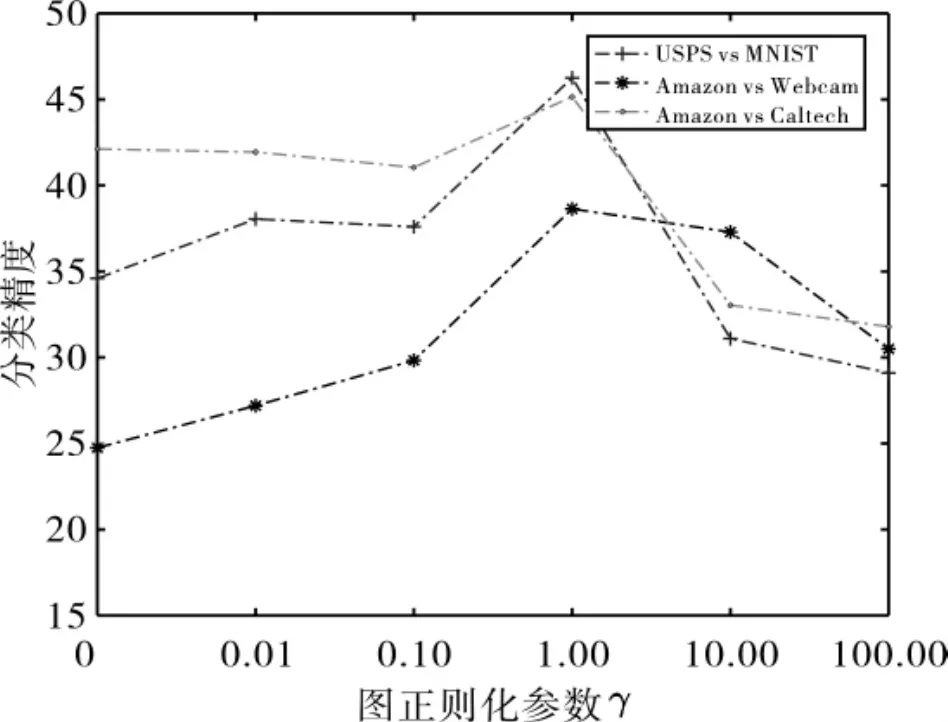
图2 正则化参数γ对分类精度的影响Fig.2 Influence of regularization parameters on classification accuracy

对于迁移性参数,设置K=128,γ=1,=0.01,结果如图3所示.可以发现μ取1×105时具有较好的分类效果；μ趋向于0时,即不考虑两域的分布差异,会导致分类精度降低；μ取值过大时,会忽略特征的几何特征和局部性,亦会导致分类精度的下降.

图3 迁移性参数μ对分类精度的影响Fig.3 Influence of transfer parameters on classification accuracy

对于稀疏性参数λ,固定K=128,μ=1×105,γ=1,实验结果如图4所示.可以发现在λ取0.01和0.1时分类效果较好；该参数主要用于控制编码的局部性特征,λ过小,忽略图像的局部性信息；λ过大,会导致编码中零向量增多,这些情况均会影响图像的分类精度.

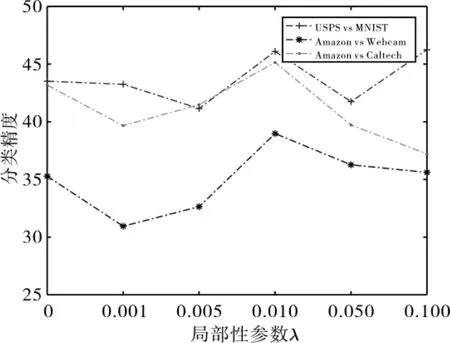
图4 局部性性参数λ对分类精度的影响Fig.4 Influence of local parameters on classification accuracy

同时为了检验迭代次数对目标模型的收敛度的影响,设NT=20,观察目标函数收敛值的变化趋势,可以发现目标模型是逐渐收敛的,如图5所示,表明了本文方法的有效性和可行性.

图5 迭代次数NT对目标函数收敛度的影响Fig.5 Influence of iteration times on convergence of objective function

4 小结

本文提出一种迁移局部线性编码的图像表示方法,该方法将迁移稀疏编码与局部约束项相结合,保留数据域的几何特征和最小化域间分布差异,且进一步引入编码的局部约束项,将样本集映射到本地坐标系中以最小化特征的重构编码,学习更具代表性的图像表示,保证了编码的局部平滑性和良好的特征重构性,进一步提高了跨域图像分类精度.在目标模型的求解上,本文利用特征符号搜索法和拉格朗日乘子法分别求解稀疏局部编码和字典基.在三个跨域图像数据集USPS vs MNIST、Amazon vs Webcam和Amazon vs Caltech上进行实验,实验结果证明了本文方法的有效性.