考虑故障相关性的风电机组维修策略
逯红霞,张蕊萍,董海鹰,2
(1.兰州交通大学 自动化与电气工程学院,甘肃 兰州 730070; 2.兰州交通大学 新能源与动力工程学院,甘肃 兰州 730070)
0 引言
由于风电机组结构的复杂性和运行环境的多样性,导致各子系统故障频发。 制定科学合理的维修策略是风电机组运行维修的关键问题。 传统的状态维修策略和定期维修策略明显存在过修和欠修问题,且各子系统之间缺乏相互协调,导致风电机组的维修成本一直高居不下[1]。 提高风电机组各子系统的供电可靠性是风电机组运行管理的重点关注问题。文献[2]提出了一种基于风电场期望出力的可靠性评估方法。 文献[3]假设风电机组各重要部件间的故障互不影响。 实际上各部件间的故障具有相关性,因此,基于故障相关性的可靠性建模,在一定程度上更能确切地评估风电机组各系统的运行状况。
风电机组各子系统的维修在经济方面存在一定的关联性,针对机会维修策略,国内外研究者进行了一系列的相关研究。 文献[4]基于可靠度的机会维修策略,节省了风电机组的维修总成本。 然而,机会维修策略忽略了风电机组各子系统的劣化过程对状态监测信息的影响。 因此,实时反映部件运行状况的状态维修策略逐渐被提出[5],并应用于风电机组的维修研究中。 Jardine A K S[6]首先提出了威布尔比例失效模型,将设备监测到的历史数据融合到状态维修中,然后,以此为根据,制定了设备的最优维修策略。 然而,风电机组的各子系统中存在容易受其他子系统影响的薄弱环节,同时也存在不容易受其他子系统影响的核心环节,如果各子系统只使用状态机会一种维修策略,会造成风电机组的运维成本高居不下。
基于以上问题,本文提出了考虑故障相关的风电机组维修策略。 借助被影响度描述各子系统被其他子系统故障影响的程度,将被影响度值高的子系统采取状态机会维修策略,将被影响度值低的子系统采取定期维修策略。 运用故障有向图理论和全概率公式推导出子系统的综合可靠度模型,建立考虑故障相关性的风电机组状态机会维修模型和定期维修模型。 通过Matlab 的算例仿真分析,验证了考虑故障相关的风电机组维略策略在节约维修成本方面的有效性。
1 故障相关性分析
1.1 故障相关被影响度计算
由互联网页面之间的连接关系来计算各个页面的重要程度称为Pagerank 算法[7],PR 值表征各个页面的重要度指标。 如果将风电机组的故障相关关系作为各个页面之间彼此的连接关系,那么在一定程度上,风电机组子系统受到其他子系统故障传递而发生故障的概率可以用PR 值衡量。若子系统受其他子系统故障影响的可能性增大,此系统的重要度也随之而增大。 由于Pagerank 算法是基于“入度”(其他子系统导入本子系统的链接数量)的,所以PR 值与入度成正比例关系。 考虑故障传递的风电机组子系统被影响度 (CK)同样与入度成正比例关系,因此,CK 值与PR 值相等,那么CK 值便可根据计算PR 值来求取。
子系统的PR 值为
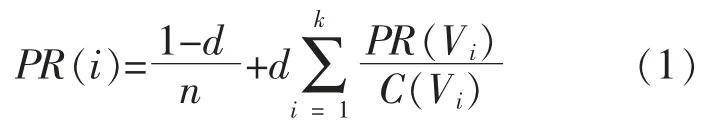
式中:n 为子系统的个数;d 为阻尼因子,代表页面沿着链接方向进行传递的概率,一般按经验值取0.85;C(Vi)为子系统节点 i 的出度,V1,V2,…,Vk为能够链入系统i 的系统。
若指定一个n 维向量PR,各子系统节点的PR 值分别由向量的分量表示。
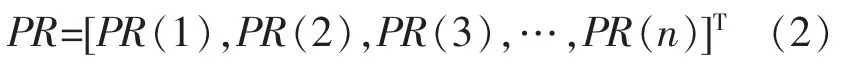
PR(x+1)为经由第 x+1 次迭代所得到的 n×1 阶矩阵,假设初始PR 值都是1。
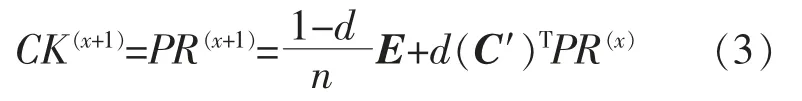
式中:E 为元素全为 1 的 n×1 矩阵;C′为根据邻接矩阵变换所得的状态转移矩阵。
1.2 风电机组故障相关性分析
根据故障关联关系和有向图理论,风电机组的故障传递关系如图1 所示。
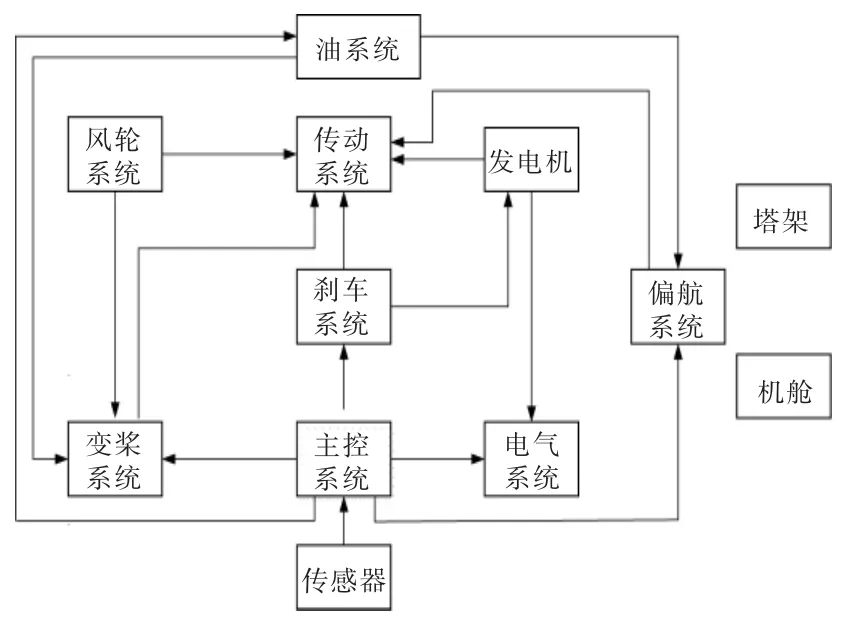
图1 风电机组的故障传递关系Fig.1 Fault transfer relationship of wind turbine
双馈风电机组有风轮系统、电气系统、刹车系统、变桨系统、传动系统、发电机、主控系统、油系统、偏航系统、传感器、塔架、机舱12 个子系统。首先,风能经由风轮转化为机械能,较高转矩、较低转速的机械能通过齿轮箱变速成高转矩、 高转速的机械能。 其次,机械能通过发电机变成电能。最后,电能经过升压器和并网装置传输到电网中。根据风速的波动及电网调度的需求,变桨系统、主断路器、变频器和并网装置等由主控系统控制。
2 风电机组子系统可靠性建模
2.1 子系统综合故障率分析
若子系统A 故障导致子系统B 故障,与忽略故障相关性相比,子系统B 的故障率将会增加。因而,综合故障率是系统自身老化和受其他子系统故障传递两个原因综合产生的。
假设共有n 个子系统构成风电机组,如果将某一个子系统看作一个单元,将风电机组中除去此系统之外的其他n-1 个子系统当作另外一个组合单元,那么由全概率公式得各个子系统随时间t 变化的综合故障率为
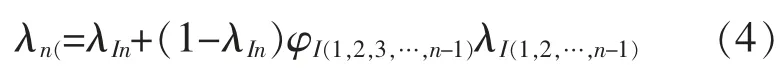
式中:λI(1,2,…,n-1)为风电机组中除自身系统以外的其他组合系统的故障率;φI(1,2,3,…,n-1)为子系统 n 受其他组合系统故障传递影响的概率。
前面已求解了各子系统的CK 值,CK 值为子系统受故障传递影响而发生故障的可能性大小,即:
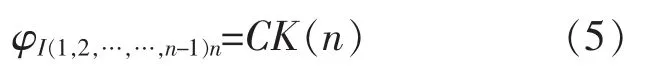
将式(5)代入式(4)得:
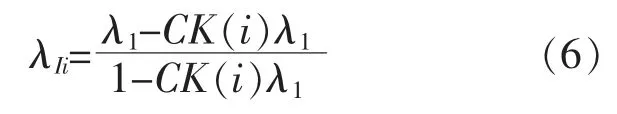
为了推导出子系统综合故障率与固有故障率之间的关系,对固有故障率函数做近似化处理。假设 1-CK(i)λ1≈1,可得:
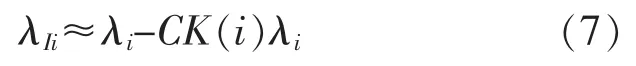
对式子(7)两边进行积分得:
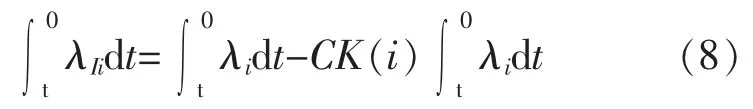
2.2 子系统综合可靠度模型
由于风电机组各个子系统的寿命分布与威布尔分布的拟合度非常高[8],因此,假设子系统的故障时间间隔服从威布尔分布。 威布尔故障分布函数 F(t)、可靠度函数 R(t)、概率密度函数 f(t)和故障率函数 λ(t)分别为
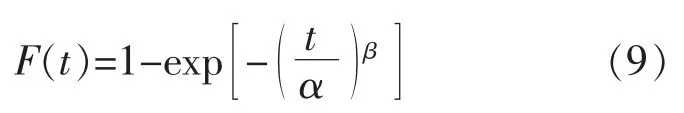
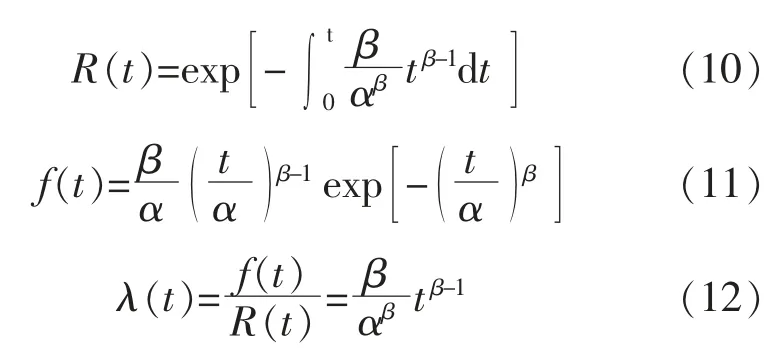
式中:α 为尺度参数;β 为形状参数。
对式(10)进行等效变换,结合式(8)得:
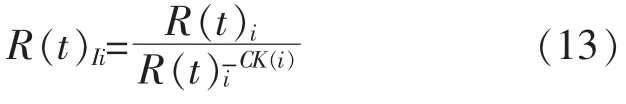
式中:R (t)i为子系统 i 的综合可靠度函数;R(t)Ii为子系统i 的固有可靠度函数为除子系统i 外,其他组合系统的可靠度函数;CK(i)为组合系统故障对子系统i 的影响度。
3 考虑故障相关性的风电机组状态机会维修策略
3.1 状态机会维修策略
状态机会维修是在单部件状态评估的基础上引入机会维修的概念,将多个处于不同状态的部件维修组合起来,达到分摊维修成本,提高经济效益的目的。 状态机会维修的基本原理如图2~4 所示。 I,j,k 子系统状态指示器分别为的机会维修阈值函数分别为的状态维修阈值函数分别为j,k 的机会维修区间分别为 ΔM(i),ΔM(j),ΔM(k)。
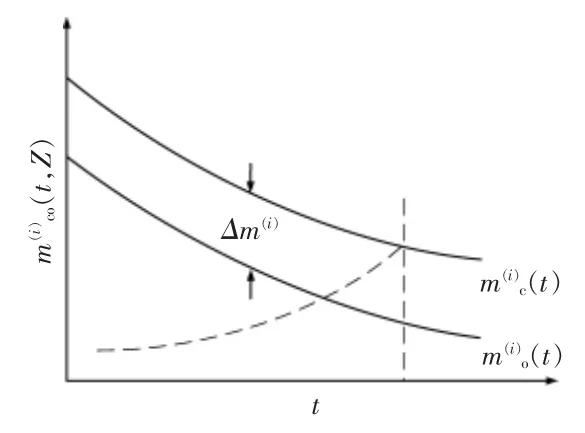
图2 i 子系统状态机会维修原理图Fig.2 State opportunity maintenance schematic diagram of subsystem i
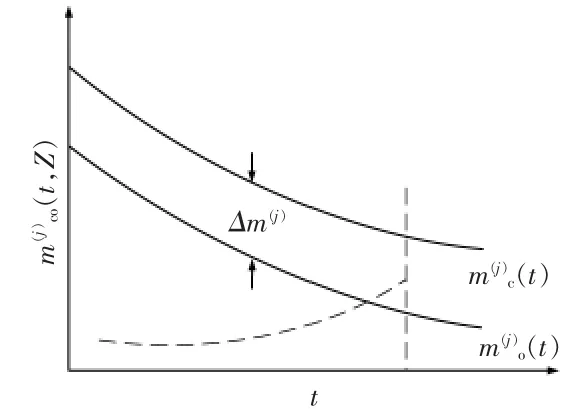
图3 j 子系统状态机会维修原理图Fig.3 State opportunity maintenance schematic diagram of subsystem j
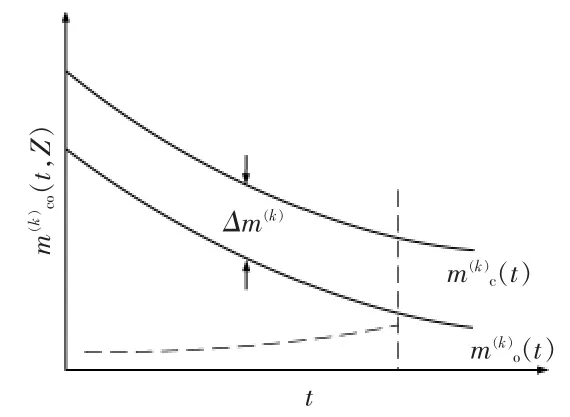
图4 k 子系统状态机会维修原理图Fig.4 State opportunity maintenance schematic diagram of subsystem k
风电机组的状态机会维修策略:
在t 时刻实施的具体维修策略: 子系统i 和子系统j 同时进行维修,而子系统k 不进行维修。由于此次状态机会维修只要风电机组停运一次,并且子系统i 和子系统j 共用人工,因此极大地节省了总维修成本。
3.2 状态机会维修阈值函数的确定
威布尔比例失效模型结合状态协变量和运行时间两个因素,可有效地评估风电机组的实时运行状况,表示风电机组的可靠性状态,模型为
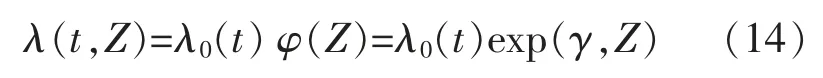
式中:φ(Z)为子系统的状态协变量函数,评估子系统运行可靠性受状态协变量 Z(t)的影响;λ0(t)为威布尔基本失效函数,只与时间 t 有关;γ=[γ1,γ2,…,γp]是由 Z(t)的回归系数构成的 P 维矢量。
由于子系统工作时间的推延,及某一些状态监测量的突变,将引起失效函数值的变化。假定一个预设阈值 Hc,当 λ(t,Z)大于 Hc时,对子系统实施状态维修,即:
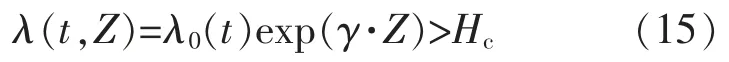
为了更加直观地观察,对式(15)做如下变换:
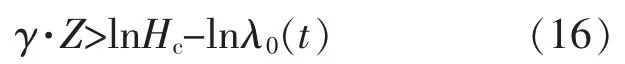
同理,得到预设阈值为Ho时的机会维修阈值函数,即:
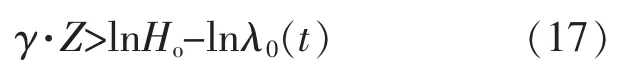
由此,可以定义风电机组子系统的状态监测器 mco(t)、状态维修阈值函数 mc(t)和机会维修阈值函数 mo(t)。
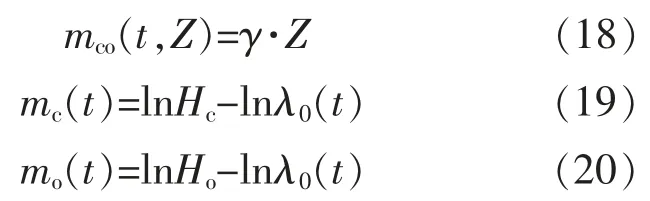
只须求取维修阈值Hc和Ho的值,便可得到其函数。
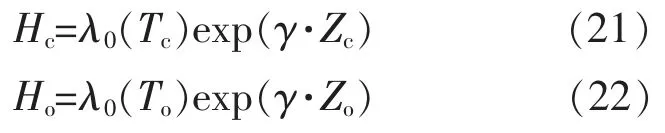
式中:Tc为最优状态维修时刻;To为最优机会维修时刻。
只需要确定Tc和To,以及分别对应的状态监测量Zc和Zo,便可以求取维修阈值。
(1)最优状态维修时间的确定
采用维修费用最小来确定最优状态维修时间。 维修在其本质上是使系统的可靠度恢复到最好状态,从一次维修到下次维修的持续时间称为维修周期Y,由于环境变化和系统更新等原因,Y其实是一个随机变量。

运用概率求取平均维修周期Y。
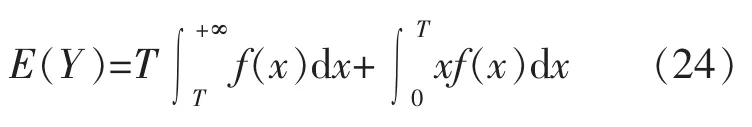
对式(24)应用分部积分,整理得到平均维修周期。
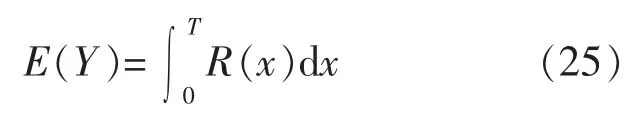
设CF为系统故障维修成本,CC为系统达到状态维修条件进行维修的总成本。 则在一个维修周期内的平均费用为
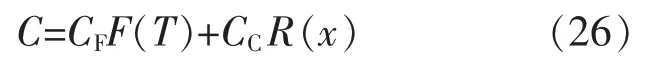
则单位运行时间内的平均维修费用为
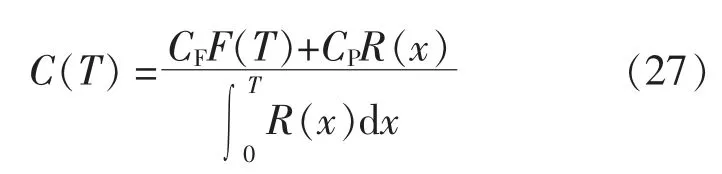
对式(27)中的 T 求导,整理得:
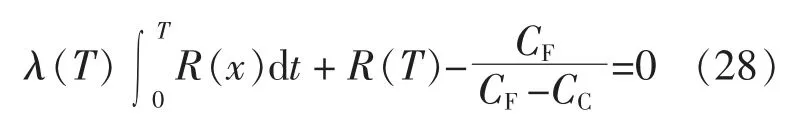
(2)最优机会维修时间的确定
采用小修成本最小来求解最优机会维修时间。 用最小维修方式,几乎不改变系统故障率函数,这就意味着系统机会维修的平均周期仍为T,T 内的平均维修费用为
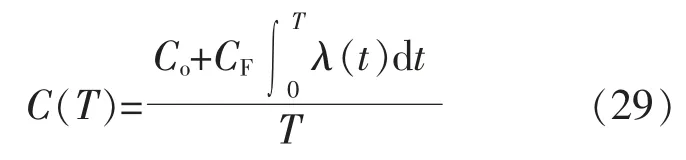
对式(29)中的 T 求导得:
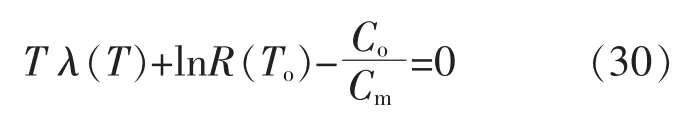
结合式(30)和(28),即可求出最优状态维修时间Tc和最优机会维修时间To。
3.3 维修成本分析
对风电机组实施状态维修记为Ac,对风电机组实施机会维修记为Ao。

对单个子系统实施状态维修,总维修费用为
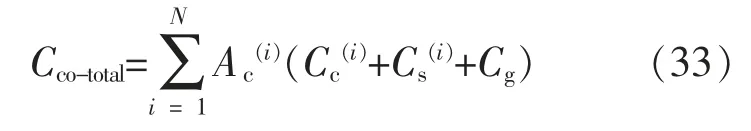
对所有子系统实施状态机会维修策略时,总维修费用为
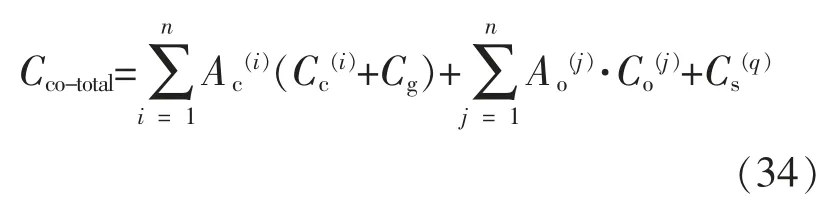
式中:Cc为状态维修费用;Co为机会维修费用;Cg为固定维修费用;Cs为停机损失。
4 考虑故障相关的风电机组定期维修策略
定期维修策略指当设备达到定期周期T 时,即使仍正常运行,也要对设备进行维修甚至更换。假设系统的累积失效函数为F(t),系统的更换或维修时间相对于工作时间很短,可以忽略不计。
长期运行单位时间的期望损失[C1(T)]为
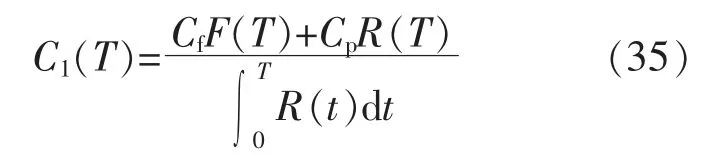
式中:Cf为事后维修的损失;Cp为定期维修的损失 (包括更换或维修部件的费用以及故障造成的经济损失和其他损失)。
求取最优的 T,使 C1(T)达到最小。
5 算例
5.1 风电机组子系统故障相关性分析
通过式(3)的计算,得到风电机组各个子系统的 CK 值及排名(表1)。
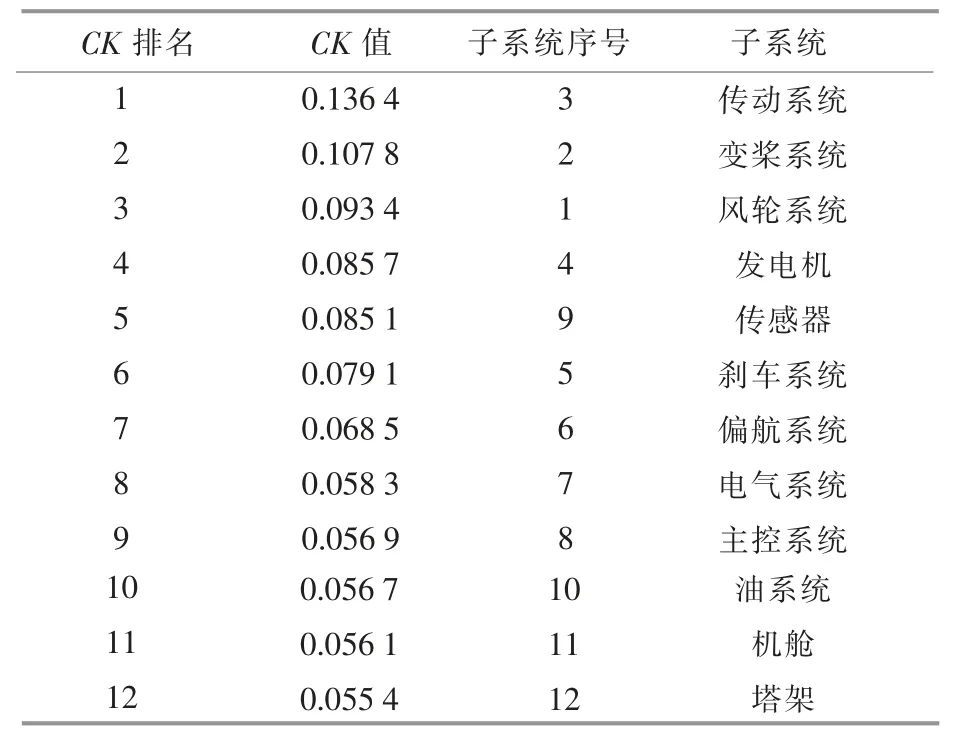
表1 子系统CK 值及排名Table 1 Subsystem CK value and ranking
由表1 可知:风轮系统、变桨系统、传动系统和发电机容易受到故障影响,属于风电机组的薄弱环节,对其实施状态机会维修;电气系统、主控系统、油系统等属于被影响度较低的系统,是风电机组的核心环节,对其实施定期维修。
现场采集了40 台风电机组各个子系统过去一年的故障样本(表2)和振动信号监测数据的变化(表3)。
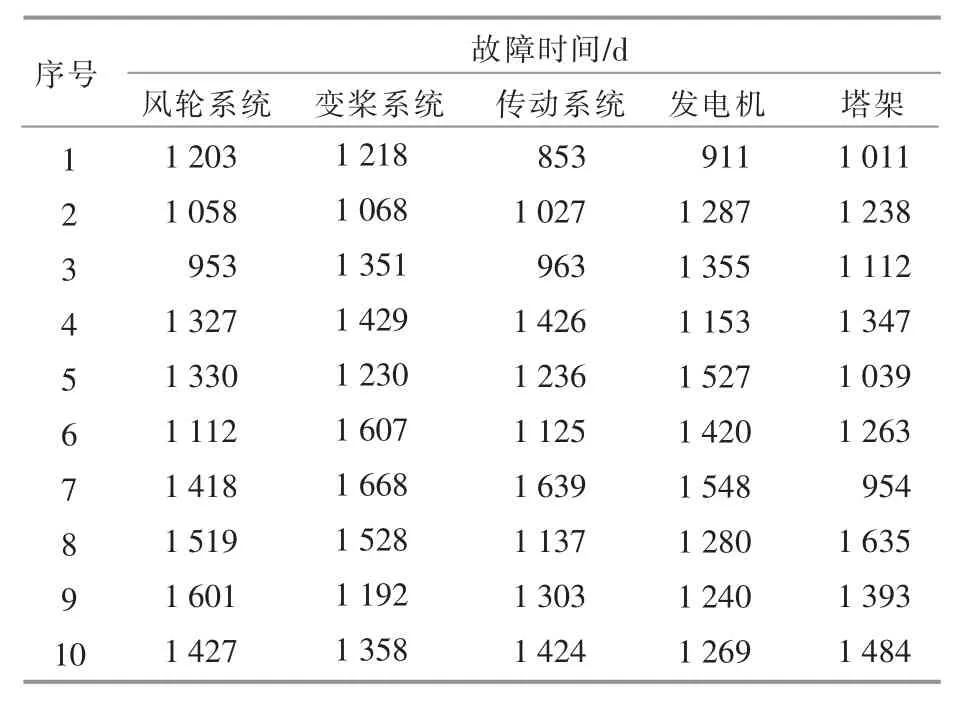
表2 子系统故障数据Table 2 Subsystem fault data
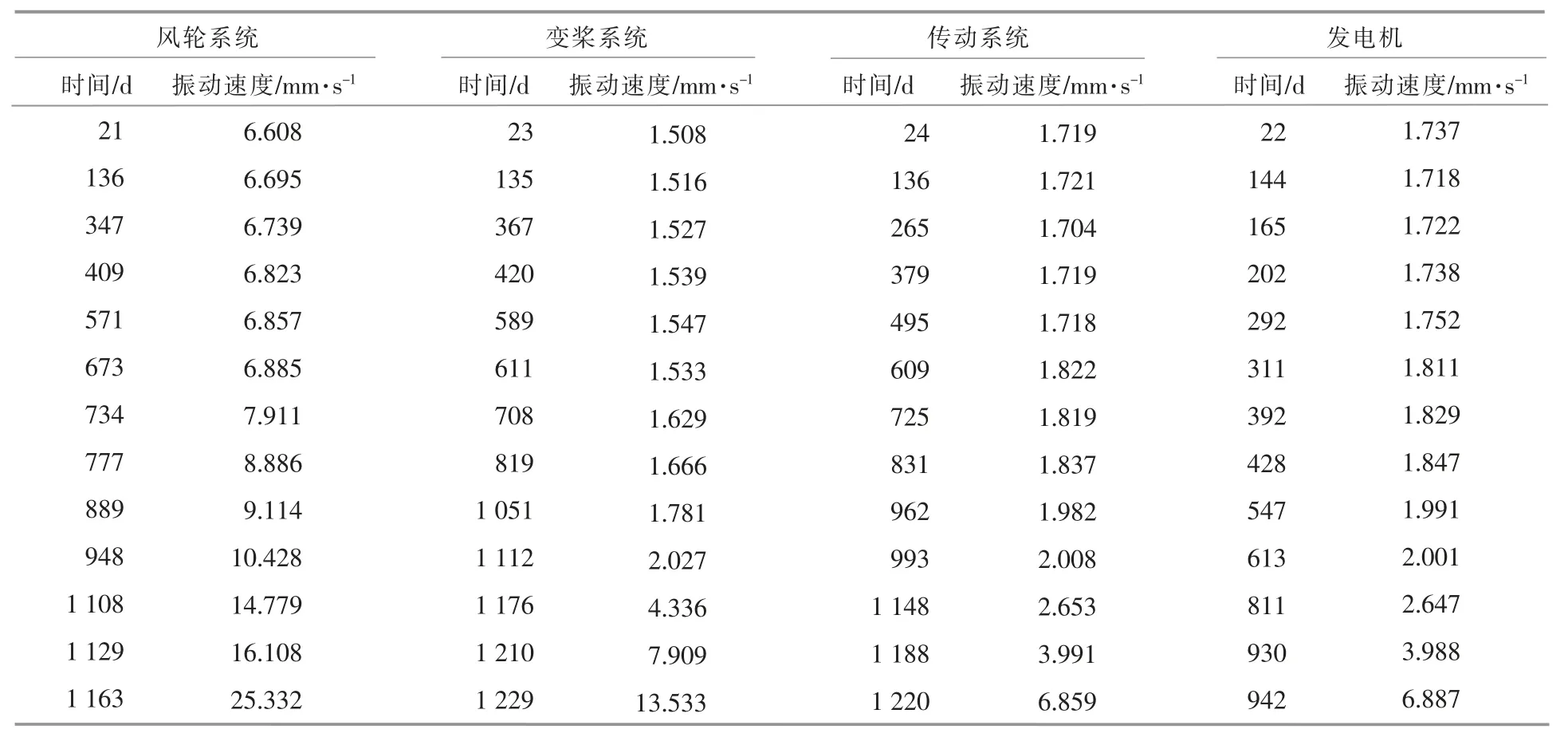
表3 子系统监测数据Table 3 Subsystem monitoring data
由表2 和表3 给出的数据,应用极大似然参数估计算法得到子系统的WPHM 参数(表4)。
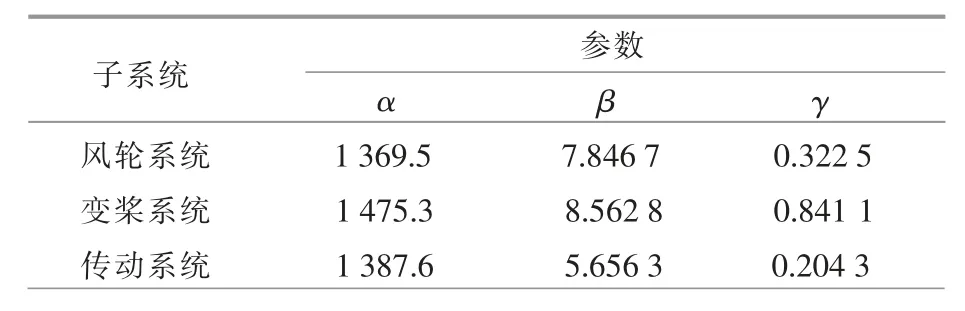
表4 WPHM 参数Table 4 WPHM parameters
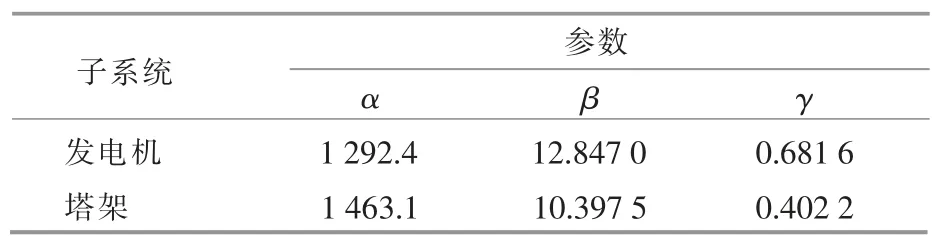
续表4
5.2 确定状态机会维修模型参数
根据风电机组各子系统的监测数据和所需维修费用(表5),可求 To和 Tc,以及各自相对应的Zc和 Zo,代入式(21),(22),便可得到各子系统的Ho和 Hc(表6)。
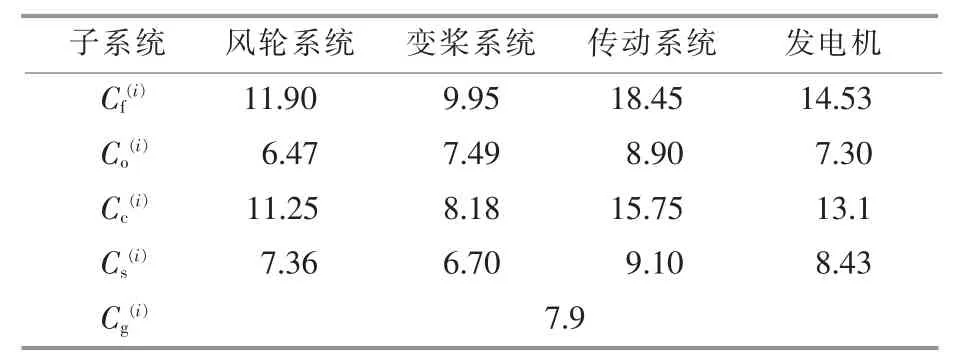
表5 各子系统的维修费用Table 5 Maintenance costs for each subsystem 万元
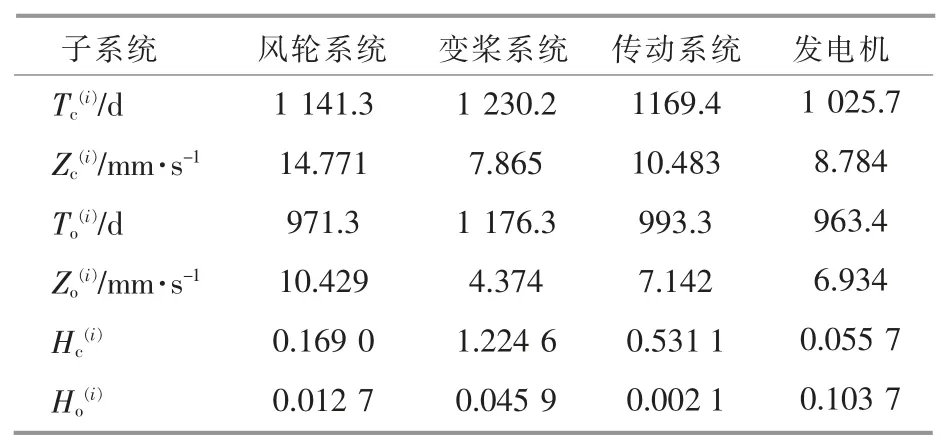
表6 各子系统的维修时间Table 6 Maintenance time of each subsystem
将表6 中求出的 Hc和 Ho代入式 (19)和(20),可得风轮系统、变桨系统、传动系统和发电机的状态/机会维修阈值函数,将状态监测数据带入 γ·Z(t)可得状态指示器数值(图5~8)。 由图可知,在722 d 时,传动系统达到了实施状态维修的条件,同时为发电机的维修创造了机会,因此,对传动系统和发电机一同实施维修,而其他两个子系统继续运行。 此次维修的总费用为40.05 万元,而如果不考虑机会维修,总维修费用为50.81 万元,节约了10.76 万元,费用节约率为21.18%。 因此,考虑故障相关的风电机组的状态机会维修在降低运维成本方面具有明显的优势。
5.3 确定定期维修模型参数
以塔架为例,假设塔架 Cf为 40 万元,Cp为8 万元,由式(35)可得 C1(T)随时间变化的曲线(图9)。 由图9 可知,当 T*=351 d 时,C1(T)取得最小值为0.017 万元/d,每年约为6.2 万元。
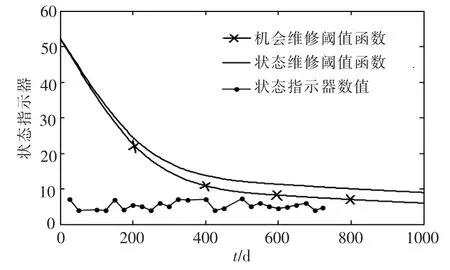
图5 风轮系统状态机会维修仿真图Fig.5 Simulation diagram of wind turbine system status opportunity maintenance
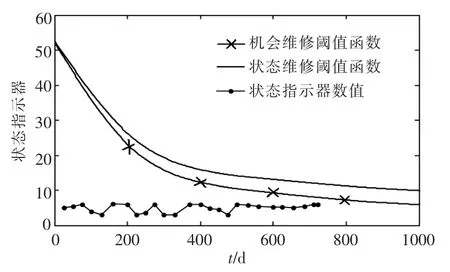
图6 变桨系统状态机会维修仿真图Fig.6 Simulation diagram of variable propeller system status opportunity maintenance
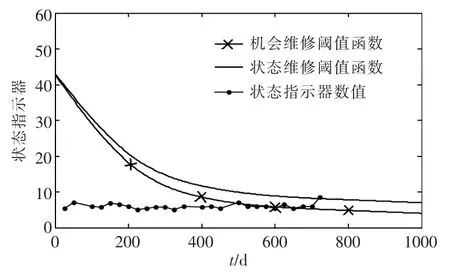
图7 传动系统状态机会维修仿真图Fig.7 Simulation diagram of transmission system status opportunity maintenance
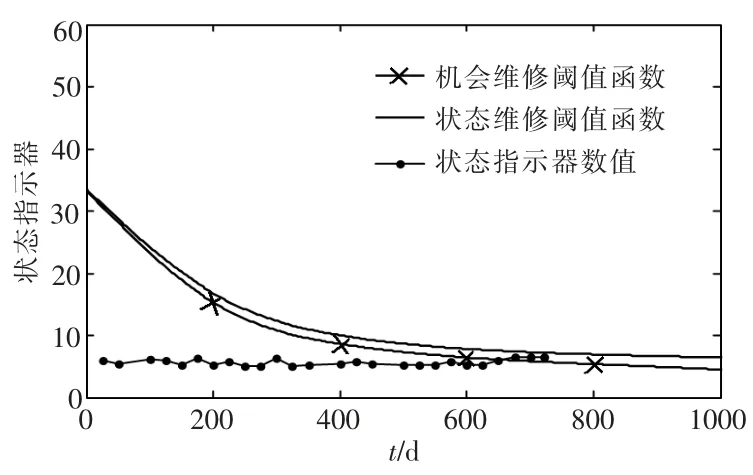
图8 发电机状态机会维修仿真图Fig.8 Simulation diagram of generator status opportunity maintenance
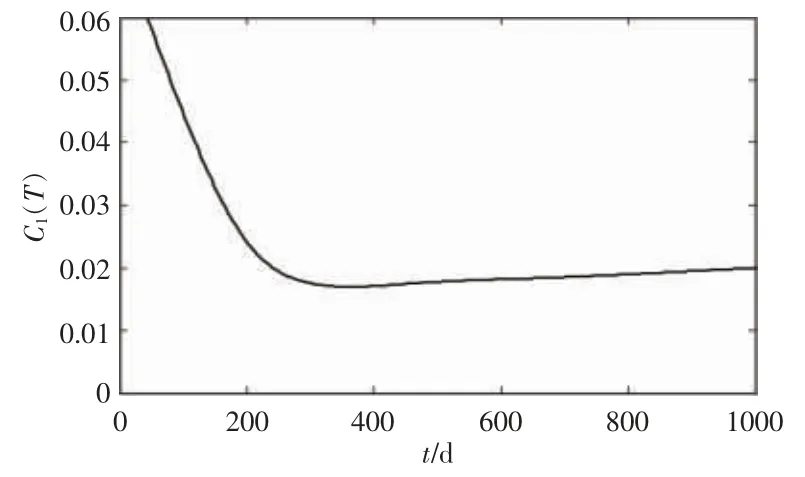
图9 塔架单位时间维修费用Fig.9 Maintenance cost per unit time of tower
6 结论
本文将风电机组子系统间的故障被影响度和状态监测信息同时融合到可靠性评价模型中,得到各个子系统的综合可靠度模型。 对比忽略故障相关性的传统模型,该模型能准确地反映子系统当前的可靠性状态。 同时,对风电机组被影响度高的子系统实施状态机会维修,对被影响度低的子系统实施定期维修,既解决了风电机组维修次数过多或过少的问题,又极大地降低了维修成本。 最后,通过仿真验证了考虑故障相关性的风电机组维修策略的可行性,为今后进一步深入研究提供了一种新方向。

