8通道复合蛇形流道质子交换膜燃料电池综合优化研究

石 磊，郑明刚，孔祥利

（1.山东建筑大学 机电工程学院，山东 济南 250101； 2.山东国惠基金管理有限公司，山东 济南 250102）

0 引言

目前，很多学者研究了流道/肋板宽度对质子交换膜燃料电池（PEMFC）性能的影响。 Shimpalee S研究了3 种不同流道/肋板宽度 （0.9 mm/0.9 mm，0.7 mm/1.0 mm，1.0 mm/0.7 mm）下 PEMFC 不同区域的应力分布特性，研究结果表明，当流道/肋板宽度为0.9 mm/0.9 mm 时，PEMFC 的热应力与机械应力响度较小[1]。 Mustukumar M 对比研究了不同流道尺寸对PEMFC 性能的影响，通过电流密度和功率密度的分析，得到了流道的最佳尺寸[2]。Cooper N J 研究了流道宽度对PEMFC 性能的影响，研究结果表明，流道宽度主要影响PEMFC 的电流密度和功率密度分布等参数[3]。

目前，有关流道尺寸对PEMFC 性能影响的研究多集中于单尺寸因素下PEMFC 性能的逐渐变化方面，这些研究无法得出PEMFC 在不同流道尺寸下的性能变化规律[4]，[5]。 此外，宽度和深度作为流道的重要尺寸参数，对流道内气体的流动和传质有着十分重要的影响。 为了进一步探讨流道尺寸对PEMFC 性能的影响，参考其他研究中的流道宽度和深度，本文将研究不同宽度-深度组合（宽度分别为 0.80，0.85，0.90，0.95，1.00，1.05，1.10，1.15，1.20 mm； 深度分别为0.80，0.85，0.90，0.95，1.00，1.05，1.10，1.15，1.20 mm）的 8 通道复合蛇形流场 PEMFC 性能的变化规律，从而为提高PEMFC 的性能提供理论支持[7]。

除了尺寸因素外，温度、进气速度和气体扩散层（GDL）孔隙度均能够对PEMFC 的性能产生影响，很多研究也证明了这些因素对PEMFC 性能的影响[7]，[8]。 但是，至今还没有关于 3 种因素对PEMFC 性能综合影响的研究。 因此，在对流道宽度-深度组合优化的基础上，本文将进一步利用统计学软件SPSS，探究温度、进气速度和GDL 孔隙度对PEMFC 的气体分布和排水性能的影响规律，并试图找出最佳的因素组合，从而保证PEMFC 在最佳的工作条件下工作，以提高PEMFC 的工作寿命。

1 模型与参数

在PEMFC 系统中，流体的流动、多孔介质中的气体扩散、 水的传递和催化剂层的电化学反应同时存在且彼此之间存在影响。因此，为了更好的模拟PEMFC，须要建立一个全面描述PEMFC 工作过程的数学模型，本文所用到的数学模型主要有质量守恒方程、动量守恒方程、能量守恒方程、组分守恒方程、电化学方程、气体组分在多孔介质中的扩散方程以及液态水的传输方程等。

（1）质量守恒方程

式中：ρ 为密度，kg/m3；ε 为孔隙率；为速度矢量，m/s；Sm为质量源项。

在PEMFC 的不同区域，Sm的数值不同，在两极的扩散层（SmGDL）以和流道出口（SmCH），Sm均为0；对于两极的催化剂层，则有：

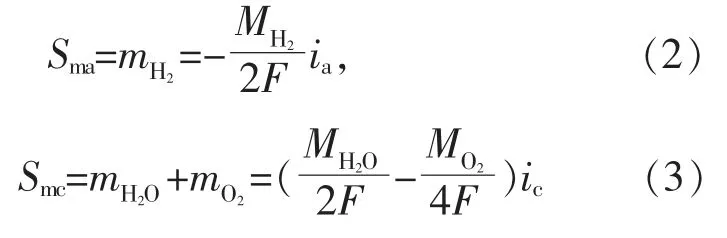
式中：M 为摩尔质量，kg/mol；F 为法拉第常数，取为96 487 C/mol；ia和ic分别为阳极和阴极的电流密度，A/m2；下标a 和c 分别表示阳极和阴极。

（2）动量守恒方程

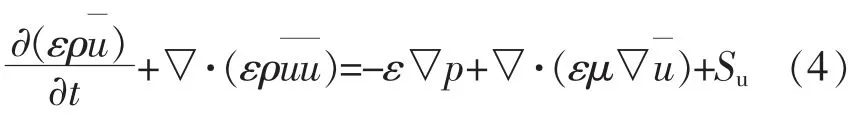
式中：p 为压力，Pa；μ 为动力粘度，N·s/m2；Su为动力源项。

在流道中，ε=1，因此，在本文的稳态模型中，在忽略对流扩散的前提下，根据达西（Darcy）定理可以将式（4）简化为

（3）能量守恒方程

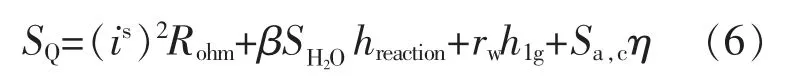
式中：SQ为能量源项；is为表面上的电流密度，A/m2；Rohm为电阻率；β 为化学能转化为热能的比率；SH2O为气态水的生成速率；hreaction为反应焓值，J/（kg·mol）；rw为水的相变速率；h1g为水的相变焓，J/（kg·mol）；Sa，c为阴极/阳极的交换电流密度，A/m2；η 为过电位，V。

（4）组分守恒方程

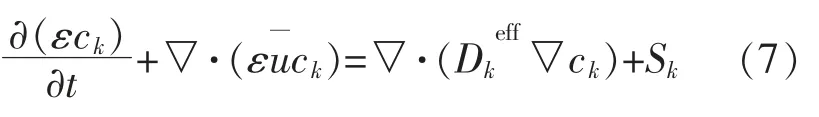
式中：ck为组分浓度，mol/m3；为组分有效扩散系数；Sk为组分源项；下标k 为组分代码，其中，阳极的组分为 H2和 H2O，阴极的组分为 O2，H2O 和N2。

在流道和扩散层中，组分源项均为0；在两极的催化剂层中，各组分源项分别为

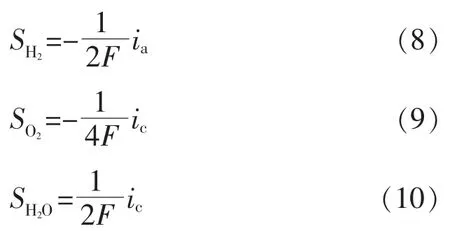
（5）电化学方程

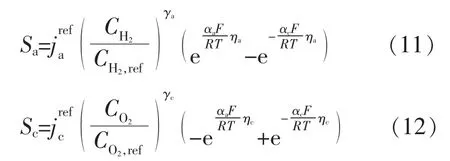
（6）气体组分在多孔介质中的扩散方程

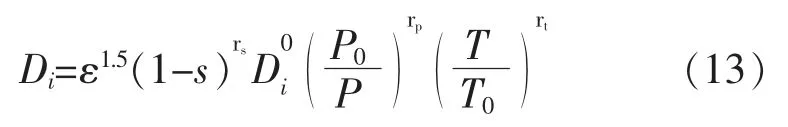
（7）液态水的传输方程

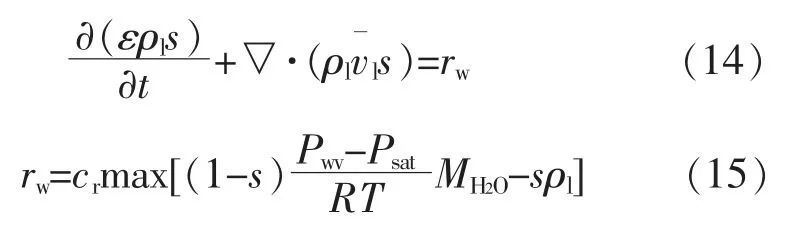
式中：Pwv为液态水的压力，Pa；Psat为饱和水蒸气压力，Pa；ρl为水的密度，kg/m3；rw为水的凝结率；s为水的相饱和度。

1.1 模型假设

为了便于计算，本文对PEMFC 的计算模型进行了如下假设： ①假设PEMFC 处于稳态运行状态； ②流道内的气体流动是理想气体的层流和不可压缩流动；③所有气体不能通过质子交换膜；④忽略重力效应；⑤GDL 和CL（催化剂层）均为均匀各向同性； ⑥将PEMFC 模型应用于蛇形通道燃料电池； ⑦流道中的少量液态水是分散的水滴。

1.2 几何参数和材料属性

本文所用模型的基础参数以及材料属性如表1 所示。

表1 模型的基础参数及材料属性Table 1 Basic parameters and material properties of model

以3.2 cm×3.2 cm 的PEMFC 单体为基础而建立的流道几何模型如图1 所示。

图1 流道几何模型Fig.1 Geometric model of flow channel

2 尺寸因素综合优化

在不同宽度-深度组合下，阴极GDL 与流道交界面处水浓度差的变化情况如图2 所示。

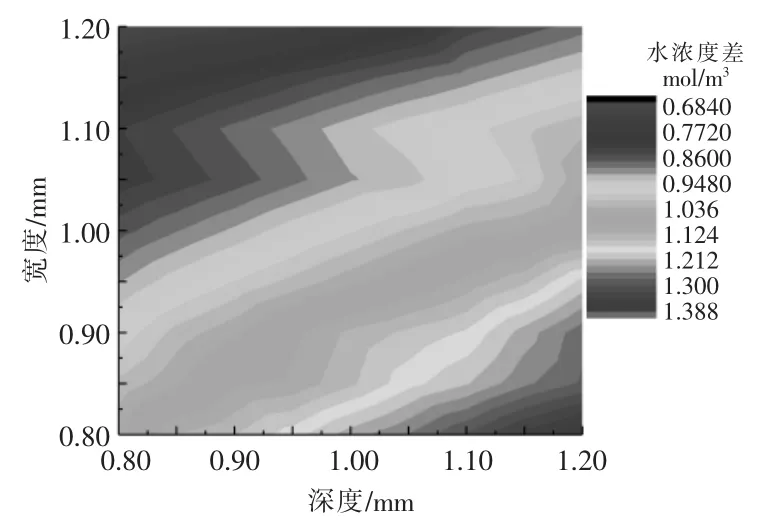
图2 不同宽度-深度尺寸组合下，阴极GDL 与流道交界面处的水浓度差分布Fig.2 Distribution of the difference in water content between the cathode GDL and the flow field at different width-depth combinations

从图2 可以看出，随着流道深度的增加，流道内水分布的不均匀程度提高，而流道宽度对水分布的影响则正好相反。 这是因为流道宽度的增加能够改善流道内的传质质量，从而使反应生成的水分布得更加均匀。 另外，流道的深度越大，气体的流速越缓慢，越不利于流道排水，容易发生水淹现象。 因此，较浅较宽的流道更有利于流道排水。

不同宽度-深度尺寸组合下，阴极GDL 的氧气浓度差如图3 所示。 从图3 可以看出，阴极GDL 中的氧气浓度差随着流道宽度的增加而急剧下降，但是流道深度对氧气浓度差的影响几乎可以忽略。因此，较大宽度的流道可以促进反应气体的分布，从而改善PEMFC 的性能，而流道深度对传质的影响不大[6]。

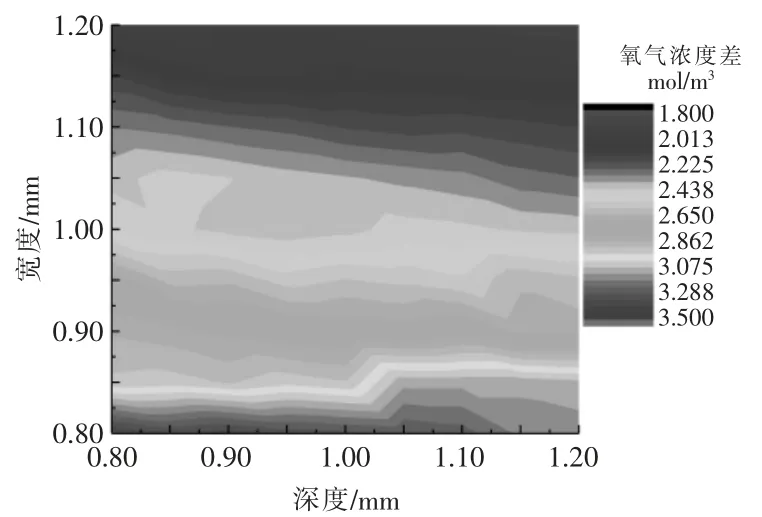
图3 不同宽度-深度尺寸组合下，阴极GDL 的氧气浓度差Fig.3 Oxygen concentration difference of cathode GDL under different width-depth combinations

不同宽度-深度组合下，阴极电极表面平均电流密度的分布情况如图4 所示。 从图4 可以看出，流道宽度是影响平均电流密度的主导因素，而流道深度对平均电流密度的分布几乎没有影响。这是因为流道宽度的增加可以提高气体分布的均匀性从而提高电化学反应的质量，流道深度的变化能够改变进气的速度而不能改变气体分布的均匀性。

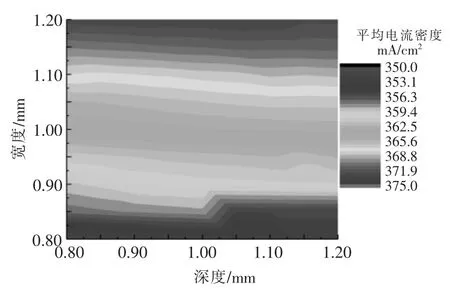
图4 不同宽度-深度组合下，阴极电极表面的平均电流密度Fig.4 Average current density of cathode electrode surface under different width-depth combinations

流道的压降是衡量PEMFC 性能的重要指标，尤其是阴极流道的压降。 如果流道的压降太高，不仅会导致气体分布的不均匀从而影响电化学反应的有效性，而且会增加外部设备的负荷，而过低的流道压降不足以提供足够的动力来除去流道中的液态水。 不同宽度-深度组合下，流道压降的变化情况如图5 所示。从图5 可以看出，流道的压降随着流道宽度的增加而逐渐降低，而流道深度对流道压降的影响相对较小。 由文献[7]，[8]可知，若流道的压降小于190 Pa，说明流道的压降处于良好状态。

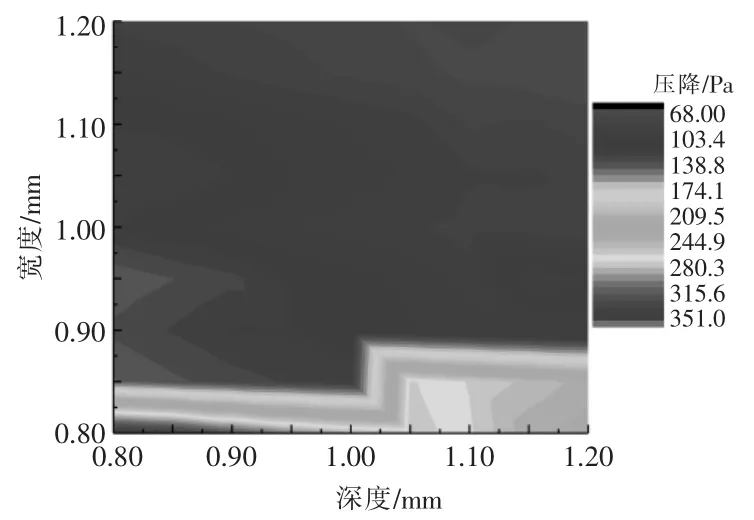
图5 不同宽度-深度组合下，流道压降的变化情况Fig.5 Pressure drop under different width-depth combinations

综上可知，通过增加流道的宽度能够有效改善流道的排水性、气体分布均匀性、最大电流密度分布和压降，从而提高PEMFC 的性能。 流道的深度对气体分布、 最大电流密度分布和压降的影响都不大，而较浅的流道有利于提高流道的排水性能。 因此，在本研究中，最佳的流道宽度-深度组合为 1.2 mm-0.8 mm。

在初始流道宽度-深度组合（1.0 mm-1.0 mm）和优化后流道宽度-深度组合 （1.2 mm-0.8 mm）下，PEMFC 极化曲线与功率密度曲线的对比如图6 所示。 从图6 可以看出，流道宽度-深度组合优化后，PEMFC 的电化学性能得到了明显的改善。

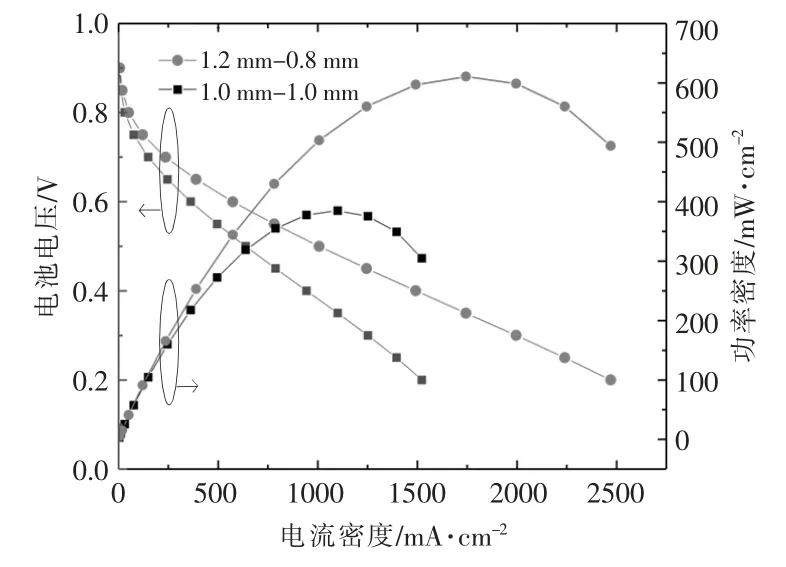
图6 尺寸优化前后，PEMFC 极化曲线与功率密度曲线的对比Fig.6 Comparison of polarization curve and power density curve of PEMFC before and after size optimization

3 外部因素综合优化

在最佳流道宽度-深度（1.2 mm-0.8 mm）组合的基础上，进一步对PEMFC 的进气速度、GDL 孔隙度和温度进行综合优化。 利用COMSOL 软件，模拟不同进气速度（1，2，3，4，5 m/s）、GDL 孔隙度（0.3，0.35，0.4，0.45，0.5） 和温度（333.15，343.15，353.15，363.15，373.15 K） 下 PEMFC 的最大水含量、最大电流密度和氧气浓度差，获得3 组数据集（每个数据集包含125 个数据），将这些数据代入到SPSS 统计分析软件进行统计分析，并通过回归方法找出输入变量 （进气速度、GDL 孔隙度和温度）对因变量（最大水含量、最大电流密度和氧气浓度差）的影响规律。

假设最大水含量、 最大电流密度和氧气浓度差分别为 y1，y2和 y3，进气速度、GDL 孔隙度和温度分别为 x1，x2和 x3。

本文共建立了3 个模型，3 个模型的输入变量均为进气速度、GDL 孔隙度和温度，因变量分别为最大水含量、最大电流密度和氧气浓度差。 3个模型调整后的 R2分别为 0.902，0.808 和 0.912，这说明3 个模型的拟合优度分别为90.2%，80.8%以及91.2%，回归方程分别能够解释最大水含量90.2%的变动，最大电流密度80.8%的变动和氧气浓度差 91.2%的变动。 3 个模型的SPSS 分析结果见表2～4。

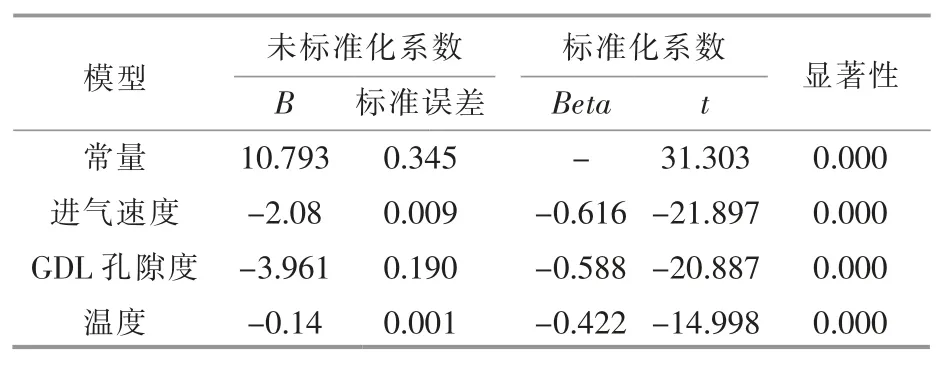
表2 进气速度、GDL 孔隙度和温度对最大水含量影响的SPSS 分析Table 2 SPSS analysis of the effects of intake velocity，porosity and temperature on the maximum water content

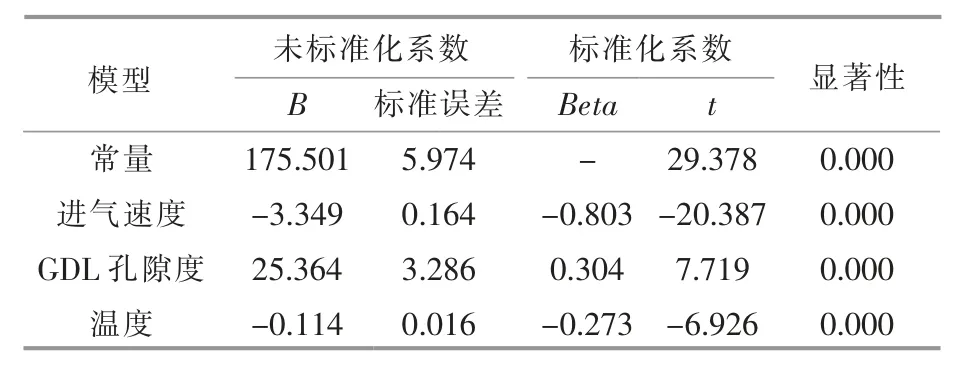
表3 进气速度、GDL 孔隙度和温度对最大电流密度影响的SPSS 分析Table 3 SPSS analysis of the effects of intake velocity，porosity and temperature on the maximum current density

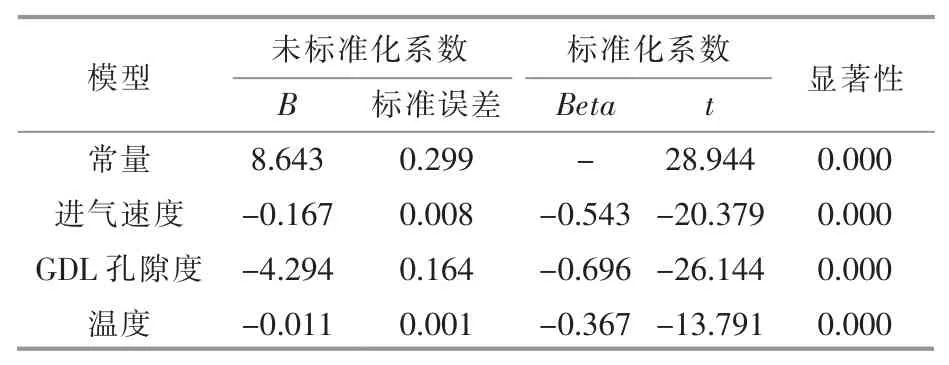
表4 进气速度、GDL 孔隙度和温度对氧气浓度差影响的SPSS 分析Table 4 SPSS analysis of the effects of intake velocity，porosity and temperature on oxygen concentration difference

从表2～4 中可以看出，每个回归系数的p 值均小于0.05，因此，每个回归系数均通过了检验。

最终得到的回归方程表达式分别为

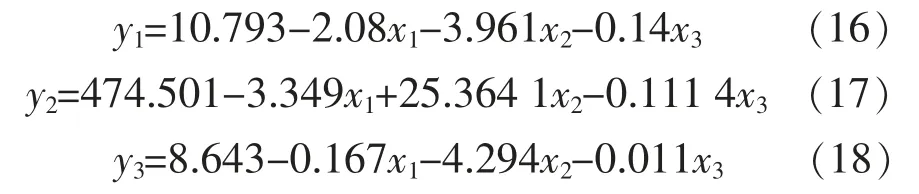
式（16）说明进气速度每增加1 个单位，最大水含量平均减少2.08 个单位；GDL 孔隙度每增加1 个单位，最大水含量平均减少 3.961 个单位；温度每增加1 个单位，最大水含量平均减少0.14 个单位。因此，3 个输入变量对最大水含量的影响程度为GDL 孔隙度＞进气速度＞温度。式（17）说明进气速度每增加1 个单位，最大电流密度平均减少3.349 个单位；GDL 孔隙度每增加 1 个单位，最大电流密度平均增加25.364 个单位； 温度每增加1个单位，最大电流密度平均减少0.114 个单位。 因此，3 个输入变量对最大电流密度的影响程度为GDL 孔隙度＞进气速度＞温度。 式（18）说明进气速度每增加1 个单位，氧气浓度差平均减少0.167个单位；GDL 孔隙度每增加1 个单位，氧气浓度差平均减少4.294 个单位；温度每增加1 个单位，氧气浓度差平均减少 0.011 个单位。 因此，3 个输入变量对氧气浓度差的影响程度为GDL 孔隙度＞进气速度＞温度。

综上可知，GDL 孔隙度对水分布、 电流密度分布以及氧气浓度分布的影响最为显著； 进气速度对水分布和电流密度分布的影响相对较大，对氧浓度分布的影响较小；温度对水分布、电流密度分布和氧浓度分布的影响均不大。

由式（16）～（18）可知：进气速度和 GDL 孔隙度的增加均可以降低最大含水量，GDL 孔隙度的增加可以增大最大电流密度，虽然进气速度的增加会使最大电流密度降低，但是，GDL 孔隙度对最大电流密度的影响是进气速度的6 倍以上，因此，在本研究中应选择较大的GDL 孔隙度；进气速度能够有效改善水分布，因此，进气速度也应当选择较大值；虽然温度对水分布、电流密度分布和氧气浓度分布的影响相对较小，但是，温度的提高能够改善催化剂的催化效率，从而加快电化学反应速率。 因此，本研究将 0.5 m/s-0.5-353.15 K 作为进气速度-GDL 孔隙度-温度优化后的组合。

宽度-深度组合以及进气速度-GDL 孔隙度-温度组合综合优化前后，8 通道复合蛇形流道PEMFC 极化曲线与功率密度曲线的对比如图7所示。 从图7 可以看出，经过综合优化后，PEMFC的电化学性能得到明显的提升。

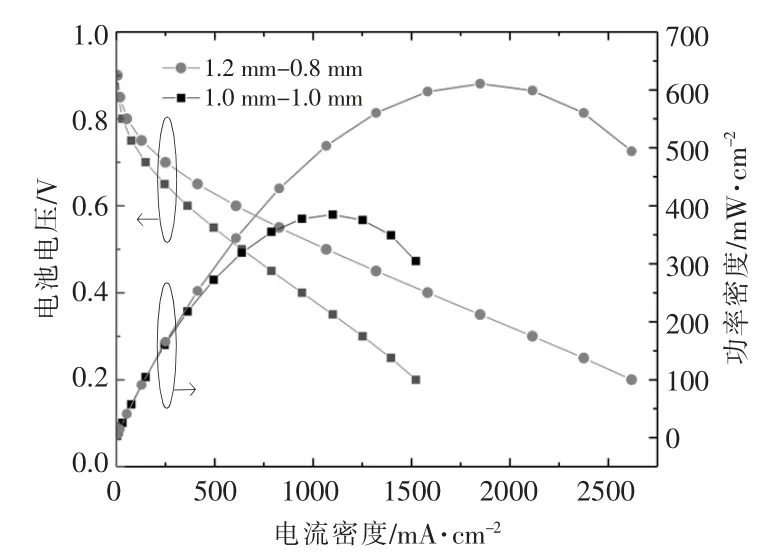
图7 综合优化前后，PEMFC 极化曲线与功率密度曲线的对比Fig.7 Comparison of polarization curve and power density curve before and after optimization

4 结论

本文研究了流道宽度-深度组合、温度、进气速度和GDL 孔隙度等综合因素对PEMFC 的水分布、气体分布能力以及电流密度分布的影响，得到如下结论。

①改变流道的宽度-深度组合能够改变8 通道复合蛇形流道PEMFC 的水分布和气体分布能力，最佳宽度-深度组合为1.2 mm-0.8 mm。

②GDL 孔隙度对水分布、电流密度分布和氧气分布的影响最大，其次是进气速度，最后是温度；优化后的进气速度-GDL 孔隙度-温度组合为0.5 m/s-0.5-353.15 K。