两种基于向量化策略SVM分类器的对比分析

薛又岷，陈春玲，余 瀚，王官中

(1.南京邮电大学 计算机学院、软件学院、网络空间安全学院，江苏 南京 210023；2.伦敦玛丽女王大学 商务与金融学院，伦敦 E1 4NF)

0 引 言

在机器学习任务中，数据大多可分为结构化数据与非结构化数据[1-3]两类。结构化数据一般又可称为行数据，是指存储在数据库中可以用二维表结构实现逻辑表达的数据，如数字、符号等。而非结构化数据指的是字段的长度不定，且每个字段中又可由其他子字段构成的数据，如文本、图像、多媒体信息等。随着计算机科学领域的多样化和不同学科间的交叉发展，越来越多的机器学习任务需要面对非结构化数据的处理问题，例如计算机视觉中对图像数据的处理，自然语言处理中对词句的处理等。近年随着推荐系统方面研究的不断发展[4-6]，针对文本数据的分析常采用的方法为文本表示法，又称文本向量化[7]。其对应于不同场景中所采用的处理方式也有所不同，大致可归为两类：词向量化与句向量化。词向量化的方法主要指的是word2Vec技术，而句向量化的方法主要是指str2Vec技术[8]。一般来说，传统的向量化技术用于预测上下文语句，但也可以通过词典形式将每个单词的出现频率记录在其中。词向量化能够在一定程度上保证词意判别的精度，但与此同时也会造成词向量与原文本中单词出现顺序无关的现象。在面对大量文本内容的情况下，词向量化常出现特征空间维度灾难与词序混乱的情况。因此，句向量化在此方面更受众多研究学者的青睐。而在机器学习算法选择方面，针对泛化性能这一重要的评价指标，文中采用十大经典分类算法之一的SVM算法[9]。SVM算法作为近十年来最有效的分类算法，通过核函数的巧妙思想，将所属不同类别之间的非线性可分数据映射到高维空间，以计算不同支持向量间最大软间隔为目标函数实现其分类目的。

金融界越来越多的学者考虑使用机器学习、量化交易等手段来预测复杂模型。然而传统的股市数据中，大量的数值型数据之间具有较强的线性关联性。若直接使用SVM分类器训练数据，很难在有限的特征空间中准确预测股价涨跌趋势。为解决这一问题，文中采用向量化策略扩充特征空间，其目的是为SVM分类器提供更多的特征依据，从而提高SVM的分类性能。

1 基本知识

1.1 支持向量机

分类算法中最基本的想法就是基于训练集在样本空间中找到一个划分超平面，将不同类别的样本分开。

定义1：给定训练样本集

D={(x1,y1),(x2,y2),…,(xm,ym)},

yi∈{-1,+1}

(1)

其中，yi为类别标记；xi为待分类样本。

SVM分类器的目的是寻找对训练样本局部扰动容忍性最好的划分超平面。换言之，即挑选分类结果最鲁棒的、对未见示例泛化性能最优的线性方程。

定义2：对给定的待分类样本空间x，可构建划分超平面，其线性方程为：

wTx+b=0

(2)

显然由式2可见，划分超平面由法向量w和位移量b决定。其中法向量w=(w1,w2,…,wl)决定了超平面的方向，而位移量b决定了超平面与坐标原点之间的距离。

定义3：样本空间中任意一点到超平面的距离用r表示。

(3)

距离超平面最近的训练点被称为“支持向量”。以二分类问题为例，所属不同类别的两个支持向量到超平面的距离之和被称为间隔，用符号η表示。SVM旨在找到具有最大间隔的划分超平面，因此可构建约束问题。

定义4：在给定间隔η的情况下，旨在找到约束参数w和b使其最大。

(4)

以上便是线性可分情况下SVM的基本型。针对式4，凸二次规划问题采用拉格朗日乘子的方式解决其对偶问题，以更高效地找到最优划分超平面。而对于样本线性不可分的情况，由于原始特征空间维数有限的情况下必然存在一个高维空间使样本可分，SVM分类器采用核函数[10]的方式，将原始样本空间映射到一个更高维的特征空间进行划分。令φ(x)表示将x映射到高维空间后的特征向量，代替式4中的样本输入x，即为引入核函数概念后的约束目标函数。

用<φ(xi),φ(xj)>表示样本xi和xj映射到高维空间后的内积，因为在拉格朗日对偶问题中为避开复杂的内积计算过程，故采用k(xi,xj)表示两种映射经过核函数计算后的结果。

定义5：核函数k(…)的定义如下：

k(xi,xj)=<φ(xi),φ(xj)>=φ(xi)Tφ(xj)

(5)

SVM分类器常用五大核函数为：线性核、多项式核、RBF核、Laplacian核和Sigmoid核[11]。对于不同的划分任务，常需实验不同的核函数以获得最优的泛化性能。

1.2 文本向量化

文本表示[12]是自然语言处理和推荐系统中最基本的任务。利用独热编码(one-hot)进行向量化操作可以将文本表示成一系列能够表达语意的向量，从而实现非结构化数据到结构化数据间的转换。目前主流的文本向量化策略分为词向量化(word2Vec)和句向量化(str2Vec)。

word2Vec计算词语间的相似度有非常好的效果，可用于计算句子或者其他长文本间的相似度。其一般做法是对文本分词后，提取其关键词，用词向量表示这些关键词，接着对关键词向量求平均或者将其拼接，最后利用词向量计算文本间的相似度。

在文本内容庞大的情况下，word2Vec方法因不具备连贯性，极易丢失文本中包含重要内容的语序信息。在此情况下可以考虑使用str2Vec方法。通过在输入层添加句向量(paragraph vector)记忆每个前序词语的判断结果，从而实现更精确的判断和预测。

2 基于向量化策略的SVM分类器

由于股票数据特征间关联性较强，且具有较强的不确定性，利用传统的机器学习方法很难准确地预测涨跌趋势。而如今日益发展的网络环境下，诸如用户评论、新闻内容等文本信息都具有潜在的价值。为了获取这些具有潜在价值的文本信息，首先提取每支股票的子论坛或新闻子板块中的文本内容关键词，对其积极、消极程度进行打分；同时，针对变化趋势明显的股票，一定具有更多的用户访问、评论和相关新闻推送量的特点对这些数据进行汇总统计，从而扩充原有的特征空间，提供潜在的特征依据。根据这一思想，文中分别利用word2Vec模型和str2Vec模型[13-15]设计了基于向量化策略的SVM分类器。

基于词向量化策略的SVM分类器：

给定一组股票样本集合X，基于词向量化策略的SVM分类器可分为2步：首先，利用向量化模型对评论区、新闻板块关键词进行打分统计，并对每只股票的点击量、评论数、新闻数进行汇总，构建5种特征项；其次，利用上述得出的特征集中前5个月的数据作为训练集，后1个月的数据作为测试集对SVM分类器进行训练。

执行过程如下所示：

算法：向量化SVM分类器

(*以单只股票为例)

输入：待扩充股票半年数据样本集合X，特征集合C

输出：C_word、ACCword(X)和C_str、ACCstr(X)

步骤1：计算每日数据中的评论数、新闻数及点击量，分别利用word2Vec模型和str2Vec模型对评论和新闻内容进行打分，构建新特征子集{Ccom_num，Cnews_num，Cclick，Ccom_rank，Cnews_rank}并添加到原特征集合C中构成C_word和C_str；

步骤2：利用SVM分类器分别对C_word和C_str前5个月内股票数据进行训练；

步骤3：利用最后一个月的数据作为测试集，计算ACCword(X)和ACCstr(X)；

步骤4：输出C_word、ACCword(X)和C_str、ACCstr(X)。

实验中所选择的词向量化模型是CBoW(continuous bag-of-words)，而选择的句向量化模型是DBoW(distributed bag-of-words)。通过计算表明，较DBoW模型而言，CBoW模型消耗的时间成本更低一些。

3 实验结果及分析

3.1 实验及分析

为了验证算法的有效性，选取了沪市半年共计3 486支股票样本进行实验。列举单支股票基本信息如表1所示。实验1是将提出的词向量SVM分类器与传统的SVM算法进行对比分析；实验2是将提出的句向量SVM分类器与传统的SVM算法进行对比分析；实验3是将提出的词向量SVM与句向量SVM进行对比分析。实验环境为PC机，双核2.1 GHz CPU，4 GB内存，Ubuntu16.04操作系统，python 3.6实验平台。

用后一天开盘价减去前一天的收盘价，若结果为正，则标记为涨；负则标记为跌。

表1 数据集的基本信息

实验1：词向量化SVM分类器(Word-SVM)与传统SVM分类器的比较。

在实验1中，将词向量化SVM分类器与传统的SVM分类器进行了对比分析，采用三种不同核函数对全部股票进行训练。列举5支拟合后保持长期增长趋势的股票，结果如表2所示。

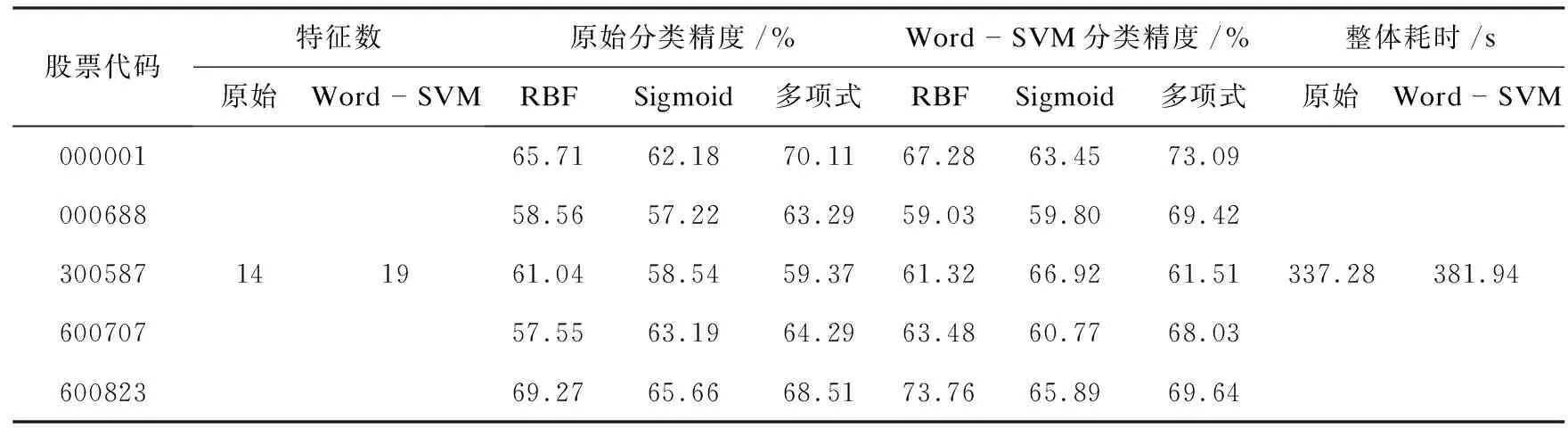
表2 词向量化SVM分类器与传统SVM分类器的比较

从表2可以看出，通过使用CBoW模型对文本内容进行处理，Word-SVM方法因添加了特征集合扩充的过程，因此比单纯使用SVM方法训练需要消耗更多的时间成本。Word-SVM方法在三种核函数的试验基础上都可以有效地提升分类精度，其中最有效的方法是使用多项式核函数。这是因为对特征集合进行扩充，为模型训练提供了更多的特征依据的同时，考虑到了将客观因素通过数值形式表示，利用隐藏的客观事件规律实现更好的预测。因此通过引用词向量化策略，可以有效地提升分类器的性能。但同时值得注意的是，股票数据每日之间具有强关联性，原始特征集之间也具有较强的线性相关性。如股票代码000001中，后一天的数据由前一天的数据、当日的大盘走势、政策因素等直接影响；五日均线、十日均线等属性之间实际上包含许多隐藏的线性关联性。

实验2：句向量化SVM分类器(Str-SVM)与传统SVM分类器的比较。

在实验2中，将句向量化SVM分类器与传统的SVM分类器进行了对比分析，同样是采用三种不同核函数对全部股票数据进行训练。列举5支股票结果如表3所示。

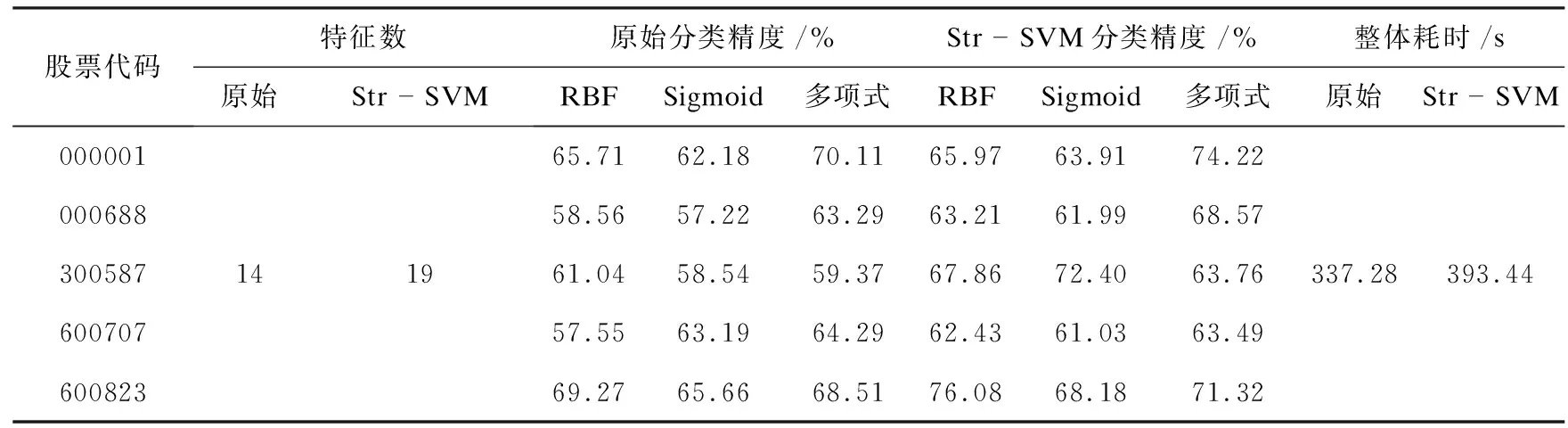
表3 句向量化SVM分类器与传统SVM分类器的比较

从表3可以看出，通过使用DBoW模型，在消耗一定时间成本的基础上对文本内容进行处理进而扩充特征空间，同样可以有效提升分类器的分类性能。

实验3:词向量化SVM分类器与句向量化SVM分类器的比较。

在实验3中，将词向量化SVM分类器(Word-SVM)与句向量化SVM分类器(Str-SVM)进行对比分析，如表4所示。

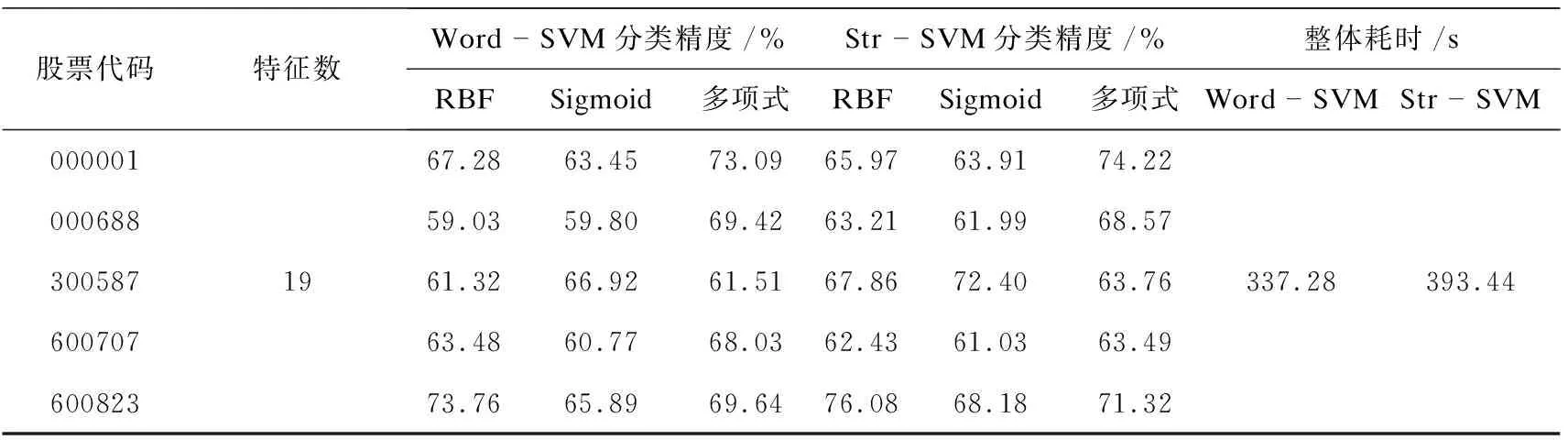
表4 词向量化SVM分类器和句向量化SVM分类器的比较

从表4可以看出，句向量化SVM分类器(Str-SVM)在三种核函数的基础上可以有效提升精度，且利用多项式核的SVM分类器进行训练，其分类精度要普遍高于利用正向贪心特征选择出的特征子集进行分类所求出的分类精度。

3.2 实验结论

为了进一步提升传统SVM分类器算法在股票预测模型中的精度，利用向量化策略，采用现有的CBoW和DBoW模型对文本特征进行词向量化与句向量化处理，并结合传统SVM分类器设计了两款启发式机器学习算法。由实验结果可知，向量化策略可以有效地将非结构化数据转换为结构化数据，从而扩充特征空间，提供更多的特征依据。且相比于词向量化，句向量化策略更能够有效地将长文本、大文本内容转换为数值数据。因为股票数据具有很多的非确定性，通过向量化非确定因素来增加特征项是目前数据处理阶段的一种重要手段。因此所提出的算法是具有现实意义的。

4 结束语

利用SVM分类器对比分析了词向量化和句向量化在股票数据特征处理方面的优劣。实验表明相比词向量化，句向量化更能够有效生成文本特征实现模型进一步的精确预测。

在文中工作的基础上，笔者将重点考虑数据预处理的方式(如：基本面等因素的介入)，同时进一步考虑使用量化交易策略与SVM分类器、神经网络等卓越的机器学习算法相结合，并将其应用到优质股票预测与推荐的问题上。