SVD推荐算法在传统服饰商城的应用
钟志攀,袁仕芳,梁荣锋,朱翡虹
(五邑大学 数学与计算科学学院,广东 江门 529020)
0 引 言
随着互联网的普及和信息技术的发展,人们日常生活可以接触到的信息越来越丰富,产生信息数据的速度也越来越快。但是“信息过载”问题也越来越严重。想要从这海量的信息中获取目的信息需要耗费大量的时间和精力。
人们解决“信息过载”问题的方法主要有建立搜索引擎、建立推荐系统(recommended system)[1-3]。推荐系统是比搜索引擎处理问题更为人性化的工具,它可以根据用户的个人爱好、历史浏览记录等为用户推荐所感兴趣的内容[4-6]。建立一个好的推荐系统可以节省用户查找感兴趣内容的时间,增强用户体验,还可以提高商品销售量。推荐系统在很多行业都有应用,例如新闻行业中的《今日头条》,个性音乐软件“网易云音乐”,尤其是电商行业,最著名的例子就有亚马逊的“尿不湿和啤酒”[7]。推荐系统在工业上最经典的应用莫过于协同过滤算法(CF)[8-9],该算法通过找到与用户有相同品味的用户,然后将相似用户过去喜欢的物品推荐给用户。
文中首先介绍了奇异值分解(SVD)和SVD推荐算法之间的联系,以及SVD推荐算法原理,在此基础上,建立了一个传统服饰商城的推荐系统。然后利用传统服饰商城的用户样本数据测试该推荐系统的性能。
1 算法原理
协同过滤算法是推荐系统中的经典算法。协同过滤算法主要分为两类,一类是基于邻域(neighborhood methods)的协同过滤算法,另一类是隐语义模型(latent factor models)的协同过滤算法[10],后者是利用矩阵分解(matrix factorization)算法实现的。
为了评价推荐算法的性能,一般使用平方绝对值误差(MAE)和均方根误差(RMSE)测试推荐系统的准确性,公式如下:
(1)
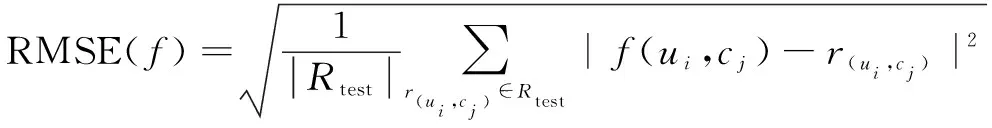
(2)
其中,Rtest表示测试数据集,ui表示用户i,cj表示商品j,r(ui,cj)表示用户ui对商品cj的评分。
1.1 奇异值分解
SVD算法是在奇异值分解(singular value decomposition)[11]的基础上建立起来的矩阵分解算法。对于矩阵A∈Rn×m,它的奇异值分解为:
(3)
其中,Σr=diag(λ1,λ2,…,λr),r=rank(A),U∈Rn×n和V∈Rm×m是正交矩阵。U的列向量称为左奇异值向量;Σr对角线上的值是A非零奇异值;VT是V的转置,V的列向量称为右奇异向量。
通常定义奇异值为σi,在矩阵Σ中沿对角线从大到小排列为:
σ1≥σ2≥…≥σr,r≤min{n,m}
σi的下降速度很快,大多数情况下,前10%甚至1%的奇异值的和就可占所有奇异值之和的99%以上,所以这里r往往远小于n和m。根据奇异值的这个性质,可以用一部分奇异值近似地描述矩阵所包含的信息,即有:
(4)
其中k≤r。
1.2 SVD算法
传统的推荐系统一般会通过用户对商品进行评价,得出评分矩阵R(rating matrix),再通过评分矩阵进行分类、预测用户喜好,从而进行商品推荐。当用户数量比较大,商品种类和数量比较多时,很难做到让所有的客户对所有的商品进行评分,此时评分矩阵R就会出现很多的缺失值。
这些缺失的评分可以看作是用户ui对于商品cj的未知的潜在评分。SVD算法的思路就是在评分矩阵R缺失的情况下,对矩阵进行分解,从而得到用户因子矩阵U(users features matrix)和商品因子矩阵C(item features matrix),最后通过矩阵U和C来预测用户对商品的潜在评分。
由式(6)推广到分解评分矩阵R,有以下等式:
Un×r=Un×nΣr×r
(5)
(6)
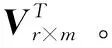
用隐语义模型来进行协同过滤的目标是揭示隐藏的特征,这些隐藏的特征能够解释观测到的评分。SVD是为了识别隐语义因子而发展起来的,然而由于大部分评分值缺失,把SVD应用到CF领域的显式评分变得相对困难。例如表1。

表1 评分矩阵R
实际情况中往往只能获得形如表1所示的评分矩阵,所有用户无法对所有商品进行评价,造成评分矩阵存在缺失值。当r(i,j)=0,表示用户i对商品j的评分缺失,如表1所示。存在缺失的现实意义就是用户尚未购买或者与某商品有一些交互动作,因此,通过预测缺失的评分,在用户尚未评价的商品中,通过用户原有的评分记录和其他用户的相似性这一先验知识,对用户没有评分的商品进行评分预测。
SVD算法在奇异值分解的基础上,将存在缺失值的评分矩阵R分解成形如表2和表3的用户因子矩阵U和商品因子矩阵C。

表2 用户因子矩阵U

表3 商品因子矩阵C
可以不用知道这两个矩阵中的因子(factors)具体是什么,第一个因子可以是商品的价格,也可以是商品的外观的美观程度。关于“因子”,可以把它认为是商品的子属性。对同一个因子进行评分,在用户因子矩阵中表示用户偏爱于这种商品的属性的程度,而在商品因子矩阵中则表示此属性在该商品反映的程度。
对于要推荐的商品,如衣服,价格是衣服的属性之一,假设这件衣服的价格很低廉,那么相对应评分就会高些,此时用户在购买衣服时十分注重衣服的价格,那么对于衣服的价格的偏爱程度就会高一点。
通过矩阵分解(可以是任何合理的矩阵分解算法),得到了上面的用户因子矩阵U和商品因子矩阵C,通过分解出来的因子评分可以预测出用户对新商品的评分,在这些新商品的评分中选取前n(Top-N)个预测评分最高的物品,构造出推荐列表进行推荐。
预测用户ui对商品cj的评分,利用用户因子矩阵U和商品因子矩阵C计算可得预测评分:
(7)
利用式(7)可以得到表4。

表4 评分矩阵
1.3 SVD算法的“学习”预测
通过上述内容,SVD算法实现推荐的主要思路是:通过矩阵分解技术将评分矩阵R分解成用户因子矩阵U和商品因子矩阵C,再通过这两个矩阵的合成从而预测用户对商品的评分。但是矩阵U和C并不是直接通过矩阵分解得出,而是通过学习的方法得到。
预测用户ui对商品cj的评分可以表示为:
(8)
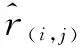
(9)
其中I∈{0,1}n×m,作为一个指示器,指示相应位置是否有评分,有评分为“1”,没有评分为“0”,最后两项是正则化项;ku和kc是常数,防止过拟合[12]。
考虑由于个体差异可能导致评分过低或过高,使用baseline predictors基准预测。将平均评分设为μ,设用户做出的评分相对于平均评分的偏差为bui,设商品cj相对于平均分的偏差为bcj,得到:
(10)
结合式(8)和式(10),有:
(11)
于是损失函数可以重新表述为:
(12)
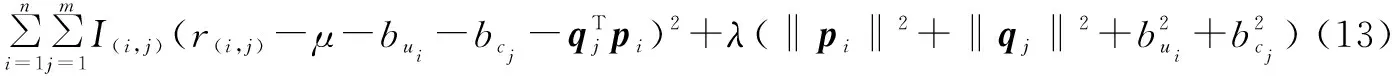
对式(13)求导到求解函数:
(14)
其中,γ为学习率。
利用评分矩阵中已知的评分求解上述函数(14),训练得到损失函数值最优时的参数,从而确定损失函数,完成对模型的训练。通过损失函数可以预测用户对商品的评分,完成推荐任务。
2 算法实现
实验是在Intel-Core i7双核处理器,CPU1 2.60 GHz,CPU2 2.0 GHz,内存4 G的计算机上进行,采用Window8.1操作系统,编程语言是Python 3.6。
2.1 数据集
实验数据来自传统汉服网站“衣缘巷”的用户统计数据。随机选取了158名用户对20件服装进行评分,评分范围是1~7。
2.2 算法实现与结果分析
算法流程如图1所示。
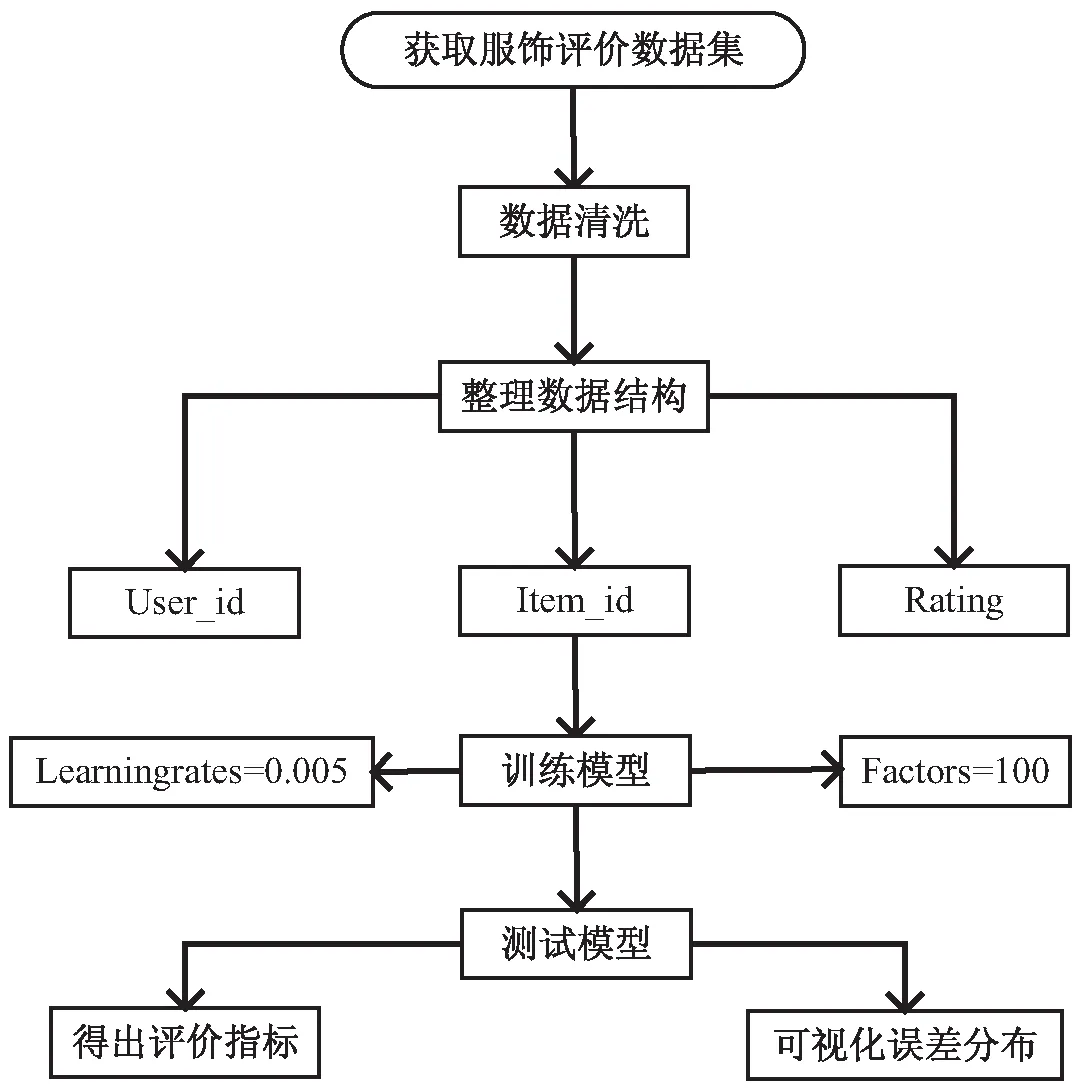
图1 算法流程
将获取到的数据进行数据清理,剔除user_id、item_id数据内容缺失的数据项。再将数据集重新整合成(user_id,item_id,rating)三元组结构。使用交叉验证[14]来验证数据,将数据随机分成三份进行三组测试,第一组实验选定其中两份数据作为训练数据,剩下的一份作为测试数据;其他两组数据也是执行同样的操作。
初始化式(13)的学习率γ为0.002,因子factors的维数初始化为100,表示将要分解的评分矩阵的因子最多有100个。模型测试指标见表5。
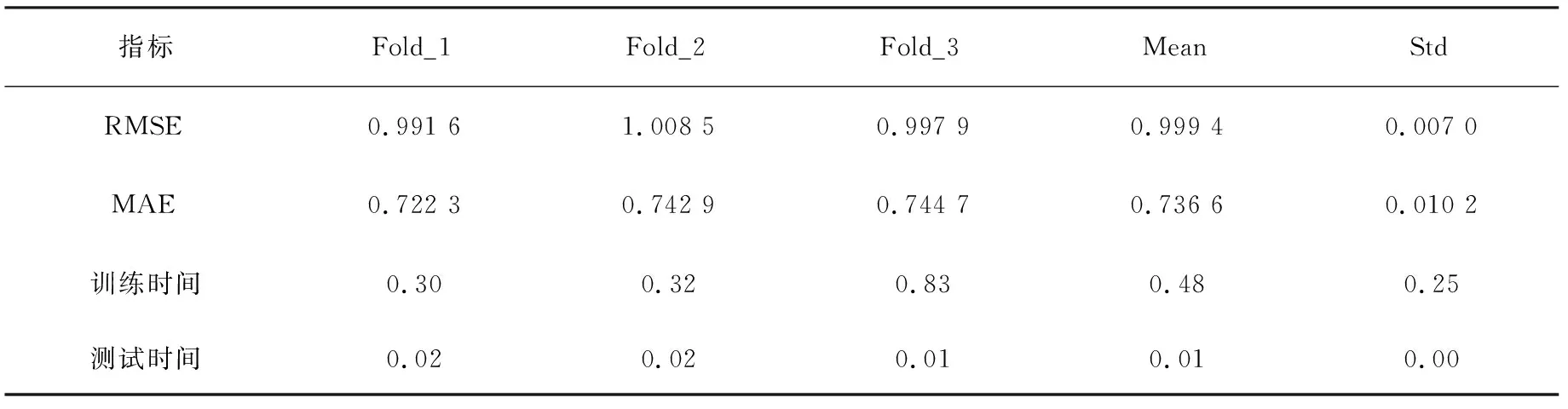
表5 模型测试指标

图2反映了实际评分和预测评分之间的绝对误差主要集中在“1”分左右,意味着该模型预测用户的评分出现的误差大部分不超过“1”。
通过计算客户对商品的实际评分和模型的预测评分之间的绝对误差占总分“7”的百分比,观察模型的总体预测性能,如图3所示。可以发现误差百分比超过50%的误差基本没有,误差百分比大部分集中在30%,其中误差百分比为10%的误差的样本数量居多。
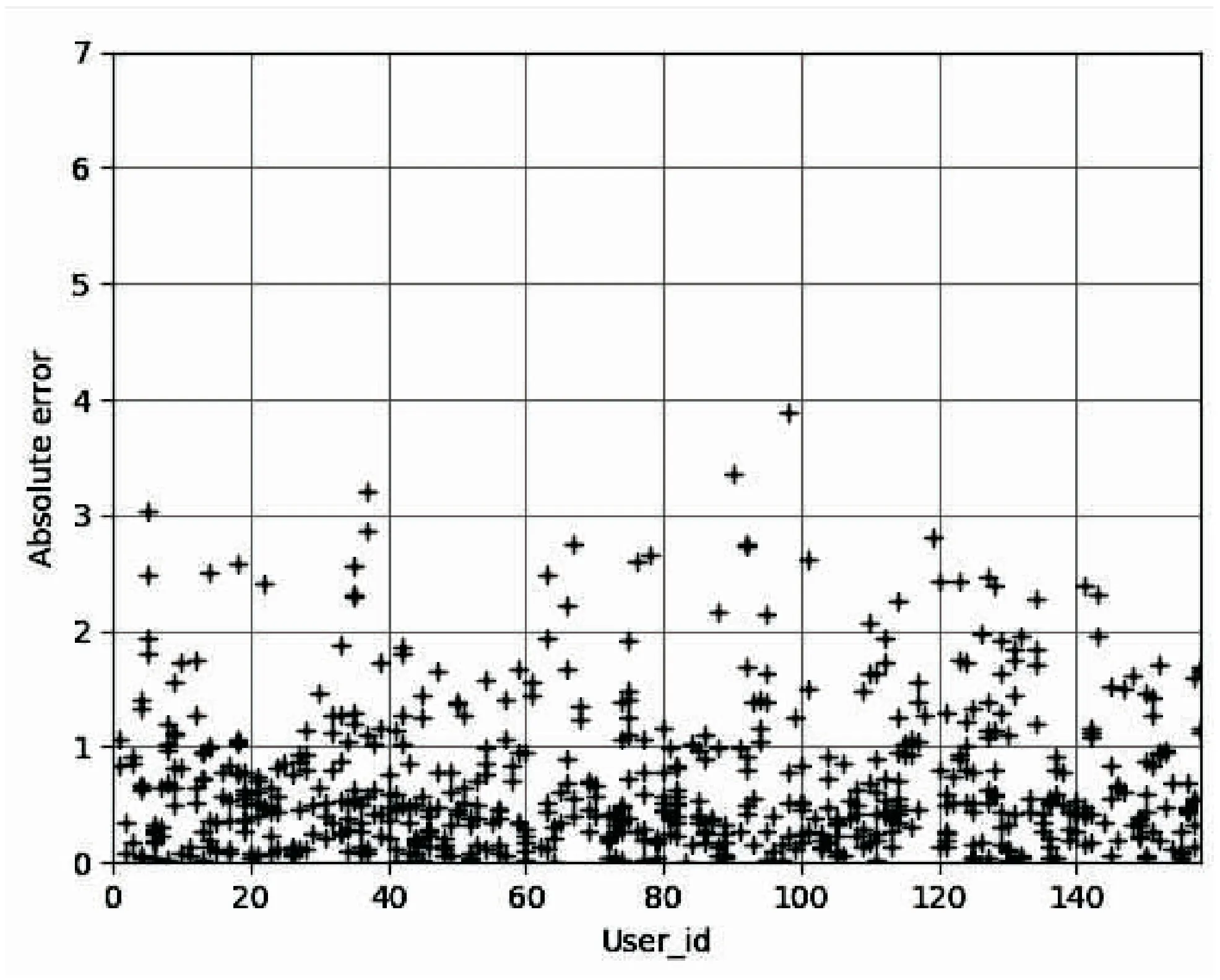
图2 绝对评分误差散点分布

图3 模型预测误差分布
3 结束语

总体来说,该模型相对于现行的其他推荐算法是可靠的。SVD算法的优势在于可以较为准确地预测用户评分,实现精准推荐。但在用户和商品基数特别
大的情况下,SVD算法会因矩阵分解的时间效率低而优势不在,表明该算法非常适合用户数量不够巨大,商品种类不太繁多的小型在线商城。

